Направления оптимизации размера прибыли организаций

В связи со сложной экономической и политической ситуацией не только в нашей стране, но и во всем мире значительное число предприятий терпят убытки, либо вынуждены снизить объемы собственной деятельности. В связи с чем остро встает вопрос о том, как можно сохранить максимум прибыли. Одним из направлений оптимизации прибыли является оптимизация ее объемов. В ходе исследования необходимо построить модель зависимости величины выручки предприятия от таких показателей, как переменные затраты и постоянные затраты предприятия. Исходными данными является величина выручки и показателей переменных и постоянных затрат предприятия за 2011-2013 гг. (таблица 1).

После того, как с помощью корреляционного анализа выявлены статистически значимые связи между переменными и оценка степени их тесноты, переходят ко второму этапу - математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. Задача решалась с использованием программы «Statistica» в режиме «Множественная регрессия». В качестве приближающей функции может быть выбрана одна из следующих:

- линейная: y = a + b × x;

- степенная: y = a × xb;

Таблица 1 - Исходные данные для построения регрессионной модели

Период	Выручка, тыс. руб.	Переменные затраты, тыс. руб.	Постоянные затраты, тыс. руб.
1 квартал 2011 г.	4240	3990	194
2 квартал 2011 г.	5220	5003	221
3 квартал 2011 г.	5913	5817	236
4 квартал 2011 г.	6210	6110	278
1 квартал 2012 г.	6832	6630	283
2 квартал 2012 г.	7210	7012	291
3 квартал 2012 г.	7540	7430	296
4 квартал 2012 г.	10313	8981	311
1 квартал 2013 г.	5910	5820	340
2 квартал 2013 г.	6820	6640	423
3 квартал 2013 г.	7340	7150	456
4 квартал 2013 г.	8470	7445	686

- показательная: y = a × bx.

Приближающую функцию программа выберет автоматически.

y – выручка;

х1 – переменные затраты;

х2 – постоянные затраты.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между результативным признаком «у» и множеством факторных признаков «х1», «х2».

На рисунке 1 показаны коэффициенты корреляции между результативным признаком «у» и множеством факторных признаков «х1», «х2».

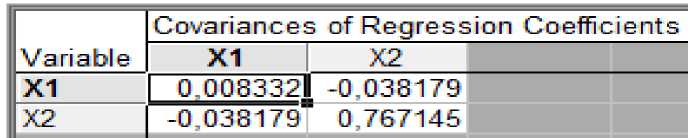
Рисунок 1 - Значения коэффициентов корреляции

Ни одно из значений не выделено красным цветом, что говорит об отсутствии зависимости между признаками, то есть между ними отсутствует автокорреляция и они могут быть использованы при моделировании.

На рисунке 2 приведены результаты построения линейной регрессионной модели, отражающей связь между размером выручки (у) и переменными затратами (х1) и постоянными затратами (х2).

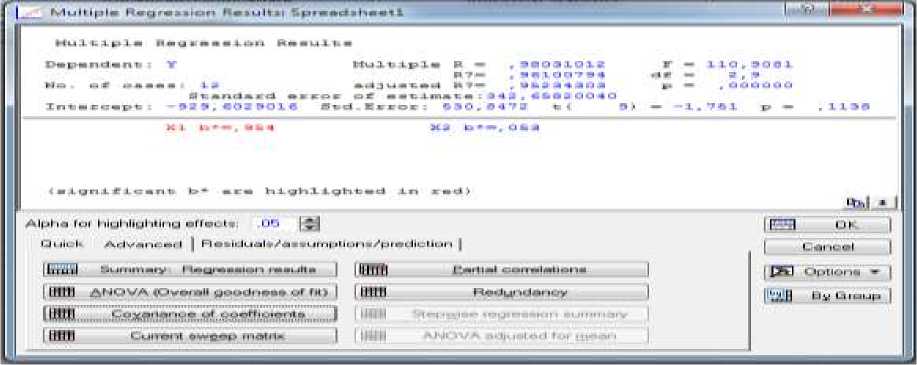
Рисунок 2 - Результаты множественной регрессии

Описание модели регрессии представлено на рисунке 3.

N=12	Regression Summary for Dependent Variable: Y (Spreadsheet!) R= ,98031012 R?= ,96100794 Adjusted R?= ,95234303 F(2,9)=110,91 p<,00000 Std Error of estimate 342,66
		Std Err of b*	b	Std Err of b		p-value
Intercept			-929.603	53 0,84 72	-1,75117	0 113834
X1	0.953950 0 074916		1.162	0.0913	12 73355	0.000000
X2	0.052891 0.074916		0,618	0,8759	0,70600	0 498057

Рисунок 3 - Описание регрессионной модели

Чем ближе значения совокупного коэффициента множественной корреляции (R) и совокупного коэффициента детерминации (R2) к единице, тем точнее уравнение множественной линейной регрессии отражает реальную связь. Как видно из таблицы 1 в нашем случае уравнение регрессии отражает связь достаточно точно, так как значения коэффициентов R и R2 практически равны единице (R=0,98, R2=0,96), то есть при построении модели были учтены важные факторы увеличения выручки. И все же полученная модель имеет свои недостатки. На рисунках 4 и 5 приведены значения p-уровней, на основании которых можно судить о значимости β коэффициентов (коэффициент признается значимым при p>0,05).

N = 12

XI

X2

Regression Summary for Dependent Variable: Y (Spreadsheet 1) R= ,99879386 R?= ,99758918 Adjusted R?= ,99710701

b*	Std.Err of b*	b	Std.Err of b	t(10)	p-value
0 9700411	,0,049270	1,025710	0,052097	19,68846	0,000000
0,030248	' 0,049270	0,590587	0,961966	0,61394	0,552966

Рисунок 5 - Описание регрессионной модели

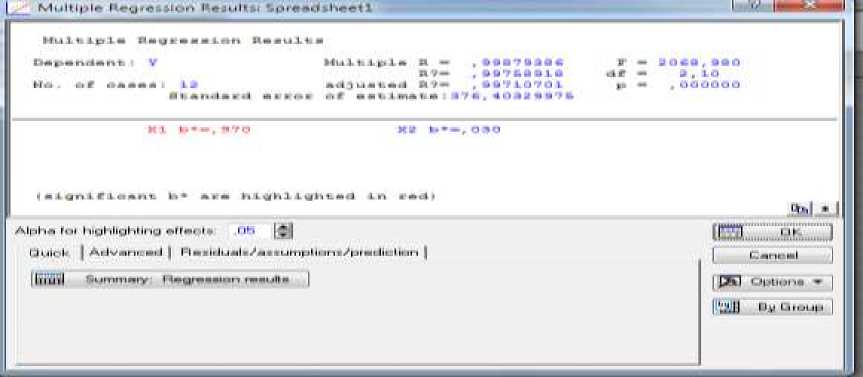
Рисунок 4 - Результаты множественной регрессии

В данном случае значимыми можно признать один коэффициент – коэффициент соответствующий значению «х1» (переменные затраты). Попробуем улучшить качество модели, исключив из нее β0. Данное уравнение регрессии отражает связь более точно чем предыдущее, так как значения коэффициентов R и R2 ближе к единице (R=0,998, R2=0,997), в данной модели наиболее значимым признается также один показатель – «х1» (переменные затраты), тем не менее, второй показатель может быть включен в модель. То есть вторую модель можно признать более подходящей для дальнейшего моделирования и прогнозирования.

Среднее значение ряда остатков близко к нулю, это очевидно, так как для построения регрессионной модели использовался метод наименьших квадратов, предполагающий минимизацию суммы квадратов остатков.

При проверке независимости (отсутствия автокорреляции) определялось отсутствие в ряде остатков систематической составляющей с помощью d - критерия Дарбина-Уотсона. Для линейной модели в качестве критических возьмём d1 = 1, d2 = 3,6. Так как в данном случае d=2,32 то гипотезу об отсутствии автокорреляции можно принять. Для характеристики точности модели воспользуемся средней относительной ошибкой. Если ошибка менее 10%, это говорит об удовлетворительной точности полученной модели. В данном случае это имеет место, то есть наша модель имеет удовлетворительную точность.

Из полученных выше результатов можно сделать следующие выводы. Модель регрессии имеет вид: y = 0,970×х1+0,03×х2. В соответствии с данным уравнением, можно сказать, что рост переменных затрат на 0,970 тыс. руб. и рост постоянных затрат на 0,03 тыс. руб. может привести к увеличению размера выручки на 1 тыс. руб.

Ширяева Н.В.

доцент

Мигурина А.П.

студент 4 курса

УлГТУ

СУЩНОСТЬ ФИНАНСОВОГО АНАЛИЗА И ЕГО ЗАДАЧИ

Содержание и основная целевая установка финансового анализа это оценка финансового состояния и выявление возможности повышения эффективности функционирования хозяйствующего субъекта с помощью рациональной финансовой политики.

Под финансовым состоянием понимается способность предприятия финансировать свою деятельность. Оно характеризуется обеспеченностью финансовыми    ресурсами,    необходимыми    для    нормального функционирования предприятия, целесообразностью их размещения и эффективностью использования, финансовыми взаимоотношениями с другими юридическими и физическими лицами, платежеспособностью и финансовой устойчивостью.

Финансовое состояние может быть устойчивым, неустойчивым и кризисным.

По мнению Савицкой Г.В., способность предприятия своевременно производить платежи, финансировать свою деятельность на расширенной основе свидетельствует о его хорошем финансовом состоянии.

Финансовый анализ – это исследовательский и оценочный процесс, главная цель которого это выработка наиболее достоверных предположений и прогнозов о будущих финансовых условиях функционирования предприятия.

"Экономика и социум" №1(14) 2015