Направления решения задачи обеспечения исправности функциональных систем самолетов эксплуатантами

Диагностирование авиационной техники преследует решение двух задач. При эксплуатации агрегатов самолета по фактическому техническому состоянию осуществляется периодический либо непрерывный контроль их параметров с целью прогнозирования интервала работы до достижения предотказного состояния. Диагностические проверки выполняются чаще в структуре периодических форм технического обслуживания.

Вполне естественно желание исследователей оптимизировать периодичность диагностирования и проверок. При техническом обслуживании с контролем параметров периодичность диагностирования связана с предот-казным допуском на эти параметры. Чем больше периодичность диагностирования, тем больше предотказный допуск, и агрегат будет отправлен в ремонт при большем значении недоиспользованного ресурса. Недоиспользование ресурса агрегата и выполнение работ по диагностированию связаны с затратами средств эксплуатантом. Кроме того, выполнение диагностирования увеличивает простои самолета на техническом обслуживании.

Известен метод оптимизации периодичности диагностирования и величины предотказного допуска, которому присвоено наименование метода экранов [1]. Применение метода сопряжено с необходимостью построения распределения диагностического параметра при значении времени налета самолета, соответствующего каждому моменту диагностирования, а также распределения моментов времени достижения диагностическим параметром предотказного значения и значения, принимаемого за отказ. Построение этих распределений крайне затруднительно, а по статистическим материалам эксплуатантов и невозможно.

Диагностические проверки функциональных систем выполняются с целью выявления неисправных и отказавших агрегатов, что существенно уменьшает долю отказов из их общего потока, проявляющихся в полете.

В данном случае цель диагностирования существенно отличается от диагностирования агрегата, обслуживаемого по состоянию с контролем параметров, а его оптимизация методом экранов становится неосуществимой.

Построение метода оптимизации основывается на использовании статистической информации о параметрах процесса технического обслуживания и эксплуатационных характеристиках агрегатов и рассматриваемой информационной системы в целом. К параметрам системы технического обслуживания в задаче оптимизации относятся следующие: периодичность контроля т _п, продолжительность контроля т _к, длительность устранения

отказов и неисправностей т _уст и соответствующие им стоимостные характеристики. В качестве характеристик агрегатов и систем принят параметр потока отказов и неисправностей системы ю и составляющие его параметры потока отказов и неисправностей, выявляемые при проверках ю _к и в полете ю _п.

Функционирование рассматриваемой функциональной системы и системы ее технического обслуживания в условиях стационарности процесса предложено представить в виде размеченного графа состояний (рис. 1).

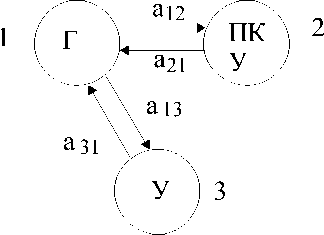
Рис. 1. Граф состояний системы с периодическим контролем: 1 – состояние готовности (исправности) реализуется в полете и во всех других случаях обеспечения коммерческого использования самолета; 2 – состояние проверок при периодическом техническом обслуживании включает устранение отказов и неисправностей, выявленных при проверках; 3 – состояние устранения отказов и неисправностей, выявленных в полете и отмеченных в замечаниях экипажа

Вероятности пребывания системы в рассматриваемых состояниях могут быть определены из решения системы дифференциальных уравнений Колмогорова:

dPlt)--(a

dt ¹

dP2 (t)

dt

dP3 (t)

dt

¹12 ^a 13 ) ^P 1 ⁽ t ^{) +} a 21 ^P 2 ⁽ t ^{) +} a 31 P 3 ⁽ t )

- a i2 P i ⁽ t ) a 21 P 2 ⁽ t )

- a13 P1 ( t ) a 31P3 ( t )

^ . (1)

Интенсивности переходов а_ij выражаются через параметры системы технического обслуживания и характеристики агрегатов рассматриваемой функциональной системы следующим образом:

^а 12

= T ^-1

п

а 21 = ^{( Т} к + ^to k ^Т уст ^)—1

а ₁₃

= to

а 31 = Т

п уст

to к = to (1 — Т п to )

to _n = to — to _K.

Подставив систему (2) в систему (1), получим следующую систему дифференциальных уравнений:

dPt)- = ^— ( ^Т п ¹ - ® п ) ^P 1 ( t ) + ( ^т к + ® к ^т уст ) P 2 ( t ) + ^т уСт ^P 3 ( t )

—^ = ^Т П 1 ^P 1 ( t ) ^— ( ^т к + ® к ^т уст ) ^{1 P} 2 ( t )

dP^ = to n P ( t ) - Т — 1т Р з ( 11

^ . (3)

В условиях стационарного процесса эксплуатации система (3) преобразуется в систему алгебраических уравнений:

^— ( ^T n ^{— to} n ) ^Р 1 ^{+ ( т} к ⁺ ® к ^Т уст ) ^P 2 ^{+ т} уст ^P 3 = 0

от типа самолета. Выводить самолет из эксплуатации специально для проверок систем нецелесообразно из экономических соображений.

При бытовавшей ранее административно-командной системе управления качество работы инженерно-авиационных служб авиапредприятий определялось по максимальному значению вероятности Р ₁ исправности самолетного парка. При этом затраты были на втором месте. В условиях рыночной экономики каждая авиакомпания имеет возможность определить для себя значение Р ₁, исходя из загруженности самолетов в обеспечении рейсов по расписанию с учетом сезонности.

В диапазоне высоких значений безотказности функциональной системы ( to = 10^-3...10^-4) изменение параметра потока отказов слабо влияет на вероятность нахождения самолета в исправном состоянии (рис. 2). Это влияние усиливается для малонадежных систем. Периодичность проверок (рис. 3) в реально допустимом диапазоне от 300 до 1 000 ч также оказывает слабое влияние на Р ₁ как при высоких, так и при низких значениях безотказности.

^{T - 1 P} 1 ^— ( ^т к ⁺ ® к ^Т уст ) ^{1 P} 2 = 0

® п P 1 — Т уСт P 3 = 0

^ . (4)

Система уравнений (4) решается относительно р_i совместно с условием нормирования

P ₁ + P ₂ + P ₃ = 1.                 (5)

Решение для состояния 1 (рис. 1) имеет следующий вид

P1 =

— 1

1 +

п

^{( Т} к + ® к ^Т уст )

+ ^to n

τ уст

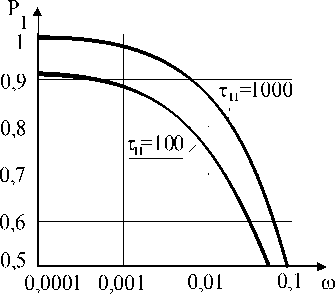
Рис. 2. Влияние параметра потока отказов на вероятность готовности изделия

В работе [2] для решения задачи оптимизации режима диагностических проверок (периодичности и продолжительности) записывается матрица интенсивности переходов и матрица доходов (затрат), задаются варианты этих матриц и отыскивается их совместное решение методом ускоренного поиска решения. Такой путь достаточно громоздкий, но для систем, реализующихся в эксплуатации, при большом числе состояний (более 4-х) и столь же большом числе характеристик агрегатов и параметров системы технического обслуживания, он может оказаться единственно возможным.

В рассматриваемом случае система имеет три состояния, и при ряде предпосылок приемлемое решение может быть получено из анализа зависимостей вероятностей пребывания системы в различных состояниях. К предпосылкам можно отнести тот факт, что при стационарном процессе эксплуатации в системах самолета отказывает ограниченный перечень агрегатов – от 1 до 5 в одной системе. В связи с этим технический персонал, за редким исключением, быстро обнаруживает и устраняет отказ путем замены агрегата. Проверки систем входят в структуру работ основной периодической формы технического обслуживания, и, следовательно, известна их периодичность в интервале от 300 до 600 ч в зависимости

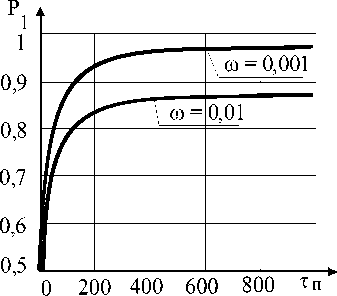
Рис. 3. Зависимость вероятности готовности изделия от периодичности проверок

Длительность устранения отказов и неисправностей Туст (рис. 4) существенно влияет на Р1. Это влияние особенно усиливается с увеличением параметра потока отказов системы. Естественно, эксплуатанты должны повышать качество технического обслуживания с целью увеличения безотказности систем. Но здесь следует помнить, что безотказность закладывается разработчиком самолета, заложенный уровень безотказности обеспечи- вается изготовителями агрегатов систем, а эксплуатант может только поддерживать этот уровень.

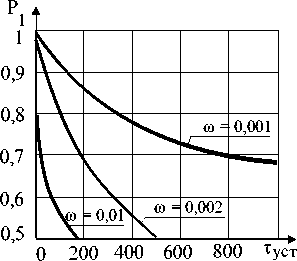
Рис. 4. Зависимость вероятности готовности изделия от длительности устранения отказов

Таким образом, эксплуатантам в системе управления затратами на техническое обслуживание доступно управление только двумя переменными: поддержанием безотказности (заданного ω ) и сокращением времени устранения отказов и неисправностей.