Направленная фильтрация для обработки изображений / видеоизображений солнца

When acquired and transmitted, images may be contaminated by noises. Therefore, images are usually denoised [Lu, Jian, et al., 2008; Sun, Xiaoli, Min Li, Weiqiang Zhang, 2011; Chen, Bo, et al., 2012; Han, Yu, et al., 2014; Wang, Jiefei, et al., 2016] before being displayed. A Gaussian filter can efficiently eliminate noises from images, especially addictive image noises, like Gaussian white noise. However, it may destroy edges of an image while denosing. The filter implements the image filtering task regardless of image content. Specifically, its weights for averaging nearby pixels over a pixel depend only on Euclidian distances of the nearby pixels to this central pixel. They are independent of intensities of pixels of an image in processing. Thus, the Gaussian filter would result in smoothed edges as it is across edges. To overcome this shortcoming of the filter, it should depend on the image content, i.e. the weights should be given not only by pixel position but also by pixel intensities of an image. For this purpose, edge-preserving filters have been developed and widely used for image processing. It can well preserve edges of objects in an image while denosing it.

A bilateral filter is the most popular of edge-preserving filters [Tomasi, Manduchi, 1998; Chen Xu, Min Li, Xiaoli Sun, 2013]. It is a non-linear, edge-preserving and noise-reducing smoothing filter for images. During image processing, the intensity value at each pixel in an image is replaced by a weighted average of intensity values of nearby pixels. The weights depend not only on the Euclidean distance of nearby pixels to the central pixel, but also on intensity values of nearby pix- els. We can thus preserve sharp edges in an image while denosing it. Despite being so popular, the bilateral filter has a number of flaws. It may suffer from “gradient reversal” artifacts, as discussed in [Durand, Dorsey, 2002; Bae, Paris, Durand, 2006]. The reason is that when a pixel (often on an edge) has few similar pixels around it, the Gaussian weighted average is unstable. In this case, the filter results may exhibit unwanted profiles around edges [He, Sun, Tang, 2013]. Another flaw of this filter is its high computational complexity.

In view of the flaws of the bilateral filter, new designs of fast edge-preserving filters have been investigated. The Edge-Avoiding Wavelets (EAW) [He, Sun, Tang, 2013] is O(n) time complexity. The filter kernel size is powers of two, which limits its application. Another O(n) time filter is known as the domain transform filter proposed by Gastal and Oliveira in [Gastal, Oliveira, 2011]. There are also some implicit filters in the literature, which are usually realized in solving optimization problems [Briggs, Henson, McCormick, 2000; Saad, 2003]. This process is often computationally expensive. He et al. have proposed a linear translation-variant filtering with explicit form, called guided filter in [He, Sun, Tang, 2013]. In the guided filter, a guidance image is additionally introduced to contribute edge preserving along with the Gaussian filter. It can be the same as the input image. In this work, we firstly apply the guided filter to a solar image/video taken by the Atmospheric Imaging Assembly (AIA) aboard the Solar Dynamics Observatory (SDO) [] for edge-preserving filtering. Then, we apply the Difference of Gaussian (DoG) filter to the original input image/video to extract details of the image/video. For the image/video enhancement purpose, the details are enlarged and then are combined by the filtered output of the guided filter to produce the final enhanced image/video.

The rest of this paper is organized as follows. Section I introduces related works. Section II describes the proposed image enhancement algorithm. Section III presents experimental results. The final section concludes this paper.

RELATED WORKS

As shown in Figure 1, the Gaussian filter is described only by a spatial kernel G s ( x i – x j ). Its weights are given by Euclidian distances of the nearby pixels to the current pixel. Pixels near the current pixel make a greater contribution than those far from the current pixel. To represent the contribution of pixel intensity to image filtering, another kernel G r ( I i – I j ), named range kernel, is defined. It is designated by an additional guided image I . This guided filter can be the same as the input image. The combination of G s and G r could filter an image in an edge-preserving manner, which results in a bilateral filter.

To overcome the gradient reversal artifacts of the bilateral filter, improvements on the bilateral filter result in the guided filter [He, Sun, Tang, 2013]. It has not only a good edge-preserving property like the bilateral filter, but also it does not suffer from the gradient reversal artifacts.

For the integrity of this paper, we outline the basic principle of the guided filter as follows:

• •    Input: a guidance image I , a filtering input image p , and an output image q ( I and p can be identical)

• •    Two assumptions:

• 1.    A local linear model between the guidance I and the filtering output q : q i = a k I i + b_k , V i e to _k . ( a_k , b_k ) are linear coefficients assumed to be constant in ω k . . Since V q = a V I , this linear model ensures that q has an edge only if I has an edge.

• 2.    Another linear relation between the output q and the input p : q_i = p_i – n_i ( n represents noise). To solve ( a_k , b_k ), an optimization is to minimize q_i – p_i while maintaining the first linear model as:

E ( a k , b k ) = E ^{(( aJ} ■ b k - p ^{) 2 + 6} a k ),           (1)

i etok where e is a regularization parameter penalizing the large ak.

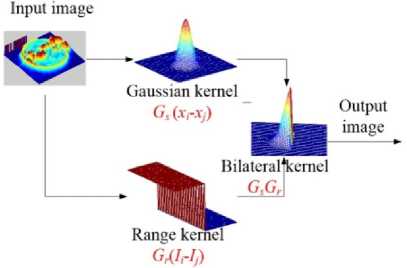
Figure 1. Flowchart of a bilateral filter

• The solution:

Ito X JiPi - HkPk ak = -------Г”-------

° k ^{+ 6}

bk = Pk - ak Hk , цk and стk are the mean and variance of I in tok, |to| represents the number of pixels in tok

For I = p, (2) becomes ak =

σ k ²

2 .

° k ⁺ 6

b k = ( 1 ^{- a}k ) H k .

At this time, the guided filter behaves as an edge-preserving smoothing operator. In the case of high variance, ст 2 >  6 , a_k ~ 1; b_k ~ 0. In the case of flat patch, ст k ^ 6 , a_k ~ 0; b_k ~ ц _k . Referring to (3), the first case can keep the pixel value of edges with high variance, and the second case is equivalent to an aver-age/smoothing operator. Thus, the guided filter has a good edge-preserving property.

IMAGE ENHANCEMENT ALGORITHMWITH A GUIDED FILTER

Taking advantage of the guided filter in edge preserving, we propose a new scheme of image enhancement (Figure 2).

First, the input image is processed by the guided filter, which gives an edge-preserved and smoothed image ( GF ( f ( x , y )). Second, details of the image, i.e. fine structures and edges, are derived by superimposing a DoG filter [Bundy, Wallen, 1984] on the input image. To enhance the image, the details are further enlarged by multiplying a scale factor. Then, these two outputs are combined together to give the final enhanced image. The reason why we employ DoG for abstracting image details is that it can provide the details while compressing noises. DoG is actually composed of two Gaussian filters with different variances. Thus, the difference between two Gaussian outputs is the component of details of an image. The scale factor is set empirically, usually ranges from 2 to 8. Users can manually set it in our designed User-Interface (UI) software.

Given the input image f(x, y), output image g(x, y), scale factor X and DoG operator with variances of ст1 and ст2, the proposed image enhancement is implemented by g (x, У ) = GF (f (x, У)) + ^ •DoG (f (x, У)). (4) The proposed algorithm is applicable to both image and video. Here, we process AIA images in the extreme ultraviolet (EUV) wave band. AIA is a part of SDO launched in 2010. It continuously observes the solar chromosphere and corona in EUV channels, and produces high spatial resolution and high dynamic range images of the chromosphere and corona. These images

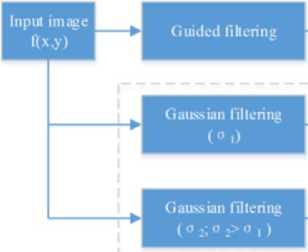
Figure 2. Image enhancement scheme with a guided filter

contain important structural information, which is of significant importance to reveal astronomical phenomena. This algorithm could improve fine structural details of an image to make it more attractive to researchers for a visual analysis. Figure 3 gives an example of AIA images. It contains fine structural details that demonstrate how a solar burst behaves. Solar burst movies can represent the evolution of solar burst activity more clearly. Figure 4 shows a movie representing a solar burst of an active region. This movie has strong impulse noise. The impulse noise can be efficiently removed by a median filter [Huang, Yang, Tang, 1979]. Figure 4, a presents a noised image, and Figure 4, b shows a denoised image obtained using the median filter. After applying the median filter, the output movie is further processed by the proposed image enhancement algorithm. In this algorithm, the guided filtering could compress some noises, especially Gaussian white noise, while preserving edges. The difference between the two Gaussian filters is that they can also compress noise as well as output details of an image. Thus, the proposed algorithm has good properties of noise suppressing, edge preserving, and detail enhancement.

EXPERIMENTAL RESULTS

To evaluate the efficiency of the guided filter and the proposed image enhancement algorithm with respect to edge preserving, we perform experiments on SDO/AIA images/videos. Matlab is used to implement the proposed algorithm. In addition, UI is designed to easily use the proposed algorithm

We employ the Graphic User Interface (GUI) of Matlab to design UI for the proposed algorithm (Figure 5). Parameters can be set by users. They are explained in Table. In Table I, the window size indicates the block size processed by the guided filter; the regularized parameter represents how strong the edge is kept after filtering as explained in (3), which usually ranges from 0.1 to 0.4. The larger ∈ , the less the edges are kept. The enhanced strength is an amplifier parameter for enhancing image edges. The larger the enhanced strength is, the stronger the edges are amplified. The image display panel illustrates the original image, the filtered image after guided filtering, and the enhanced image from left to right.

Parameters of the proposed algorithm in UI

Parameter	Explain
Window size	Processing unit of block size for guided filtering;
Regularization Parameter ( ∈ )	Lagrange factor (Eq. (4))
Enhance Strength	Factor for enlarging detail signal;
Width	Width of input video;
Height	Height of input video;
Frames	Number of frames of input video

To explain how the above parameters affect resulting images, we change the parameters and obtain resulting images shown in Figures 6 and 7. For clarity, we change only one parameter; others are fixed. In Figure 6, only the window size is changed, other parameters are fixed. Comparing Figure 6, a and b , we can concluded that a larger window size leads to less textures remaining on the solar disk surface. The reason is that the guided filtering is performed on a block basis, and thus a large block would smooth more textures. From Figure 6, b it follows that more textures are kept if the window size is small. If a texture is too heavy to interfere with our analysis, we should enlarge the window size appropriately to suppress textures. Figure 7 shows enhanced images as the enhanced strength changes while the window size is fixed. It can be seen that a high enhanced strength is better for enhanced images; however, it cannot be too high, usually lower than 16. Otherwise, noise would be significant. By comparing and analyzing a series of SDO/AIA images, we decide on the best parameter setting: window size=4, ∈ =0.2, enhanced strength=8. All of the following experimental results are obtained under this parameter setting.

Figure 8 illustrates the experimental results of SDO/AIA videos, which record the solar burst evolution. Enhancement of details in each image of the video can help users to better understand the evolution process of solar bursts or other activities. From the enhanced image, shown in the right panel of Figure 8, contours of objects and fine fibrous structures can be identified more clearly than original ones.

For demonstrating the superiority of the proposed algorithm, we compare it with the Laplacian sharpening and Unsharp Mask (USM) algorithms [Kim Sang Ho, Jan P.

Figure 3. SDO/AIA images: 171 Å ( a ); 193 Å ( b ); 304 Å ( c )

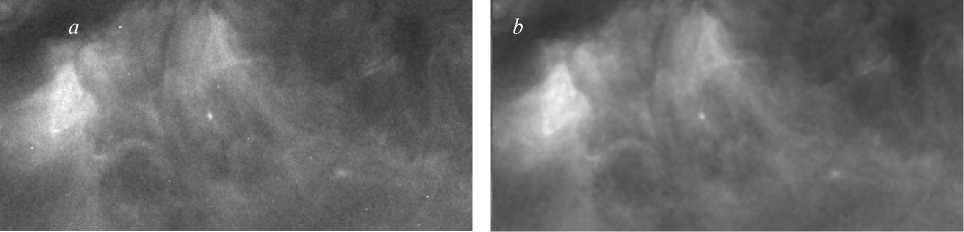
Figure 4. Solar burst movies recorded by SDO/AIA. Original image contaminated by impulse noise ( a ); image denoised by a

median filter ( b )

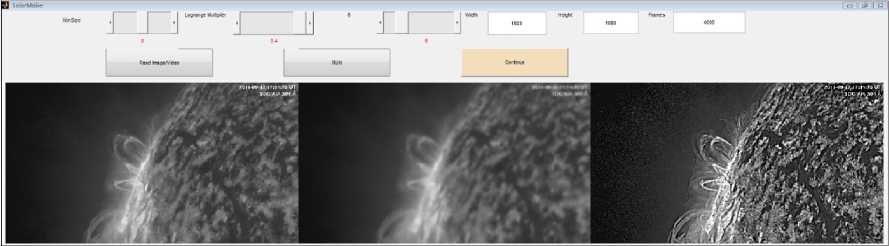
Figure 5. UI of the proposed image enhancement algorithm

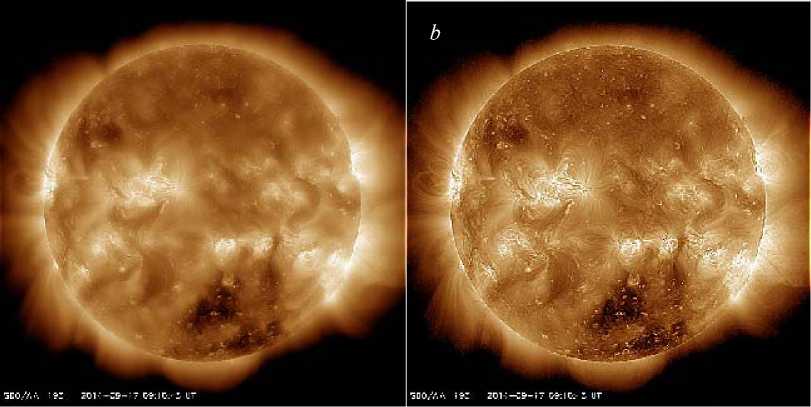
Figure 6. Influence of a window size on the resulting image (enhanced strength is fixed to 8, ∈ is fixed to 0.1). Window size = 8 ( a );

window size =2 ( b )

Figure 7. Influence of enhanced strength on the resulting image (window size is fixed to 4, ∈ is fixed to 0.1). Enhanced strength=8 ( a ); enhanced strength=4 ( b ).

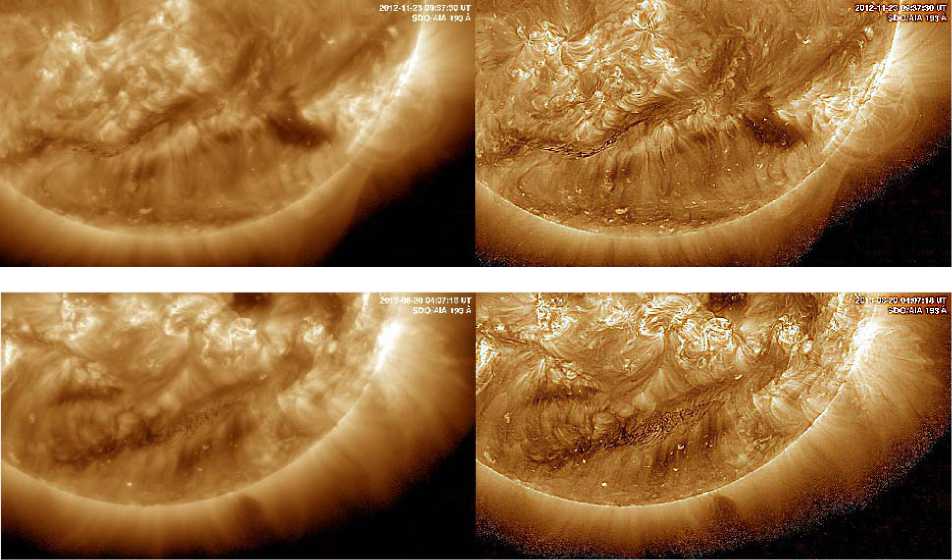
Figure 8

Figure 8 (continued)

Figure 8. Enhancement of an SDO/AIA video

Figure 9. Comparison between image enhancement algorithms: original ( a ); proposed ( b ); Laplacian ( c ); USM ( d )

Allebach, 2005; Li Xia, Zheng An Yao, Wen Shu Zhou, 2008; Li Jingna, Li Xia, 2012; Song Huijuan, Jingxue Yin, Ying Yang, 2013; Sun Jiebao, Jing Li, Qiang Liu, 2014], state-of-the-art algorithms for enhancing image edges. The resulting images are shown in Figure 9. Referring to Figure 9, the proposed algorithm can provide a better image quality beyond the benchmarks. Figure 9, c and d indicate that the edge of the solar disk can be identified and enhanced respectively by the Laplacian and USM algorithms; however, fine fibrous structures indicating pattern and evolution of a solar burst cannot be identified well, thus leading to failure of enhancement.

CONCLUSIONS

This paper has studied the guided filtering for solar radio image/video denosing and enhancement. A new image enhancement algorithm was proposed for image enhancement by using the guided filtering for edge preserving. It can provide a good perceptual visual quality for identifying fine fibrous structures of solar bursts so that we can do a physical or mathematical analysis of solar activities more easily.