Напряжения в капиллярах композита с неоднородностью непрерывного типа
Автор: Черкасов В.Д., Тюряхин А.С., Богатова С.Н.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Технические науки
Статья в выпуске: 3-4, 2005 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14718656
IDR: 14718656
Текст статьи Напряжения в капиллярах композита с неоднородностью непрерывного типа
-
С. Н. БОГАТОВА, аспирант
В ряде задач механики композитов в качестве модели представительной ячейки капиллярно-пористого композита можно выбрать (в геометрическом смысле) одиночный призматический капилляр кругового сечения [2; 3; 5]. Для такой модели ранее уже были представлены особенности макромеханики [4] и напряженно-деформированного состояния [2] ячейки из однородного материала, а также изложена методика определения эффективных модулей [3] и пористости [5] для ячеек с неоднородностью кусочно-однородного типа. В данной статье, опираясь на методы, изложенные в монографии [ 1 ], расширим класс решаемых задач и для ячеек, материал которых обладает свойством неоднородности непрерывного типа.
Расчетную модель ячейки композита представим прямолинейным капилляром, который имеет длину L , а также внутренний а и внешний b радиусы кругового сечения (рис. 1). При этом замкнутая пористость композита при достаточно большой величине отношения L/b будет равна объемной доле капала в одиночной капиллярной ячейке:
я a^L
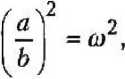
at = С2 + Q
£(г)
£(г) , —я-ат ,
г
где to — отношение радиусов капилляра.
Капилляр, в общем случае, испытывает действие как внутреннего (порового)
давления р, так и наружного давления q.
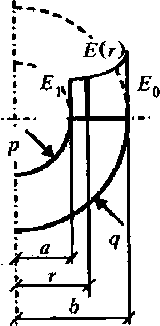
Рис. 1. Круговое сечение ячейки композита
Следовательно, при наличии осевой симметрии (статической, геометрической и в распределении неоднородностей материала) задача становится одномерной, зависящей лишь от радиальной координаты г в пределах интервала (я, Ь) ее изменения. Граничные условия первой краевой задачи примут весьма простой и лаконичный вид (см. рис. 1):
г = а, от = -р, г =b, сгг = -q,
где аг — радиальные напряжения.
Если пренебречь объемными силами, то для плоской деформации капилляра с изменяющимся по толщине материала модулем Юнга Е (см. рис. 1) разрешающее уравнение осесимметричной задачи запишется как [4]
с" + р(г)сг' + ЗтУзт = 0. (3)
Коэффициенты ^(г) и ty(r) особенно просты для так называемого несжимаемого материала, когда коэффициент Пуассона v= 0,5 = const [4]:
^(г)Л-^_ уг(г) = 0. (4)
г E
Решением уравнения (3) с учетом равенств (4) служат выражения
, Е(У) ar = С2 + CJ —-y-dr, где at — окружные напряжения.
Здесь и далее от упругих констант Е и v целесообразно отказаться и перейти к объемному модулю К и модулю сдвига G, определяемым формулами
£ . с _ Е
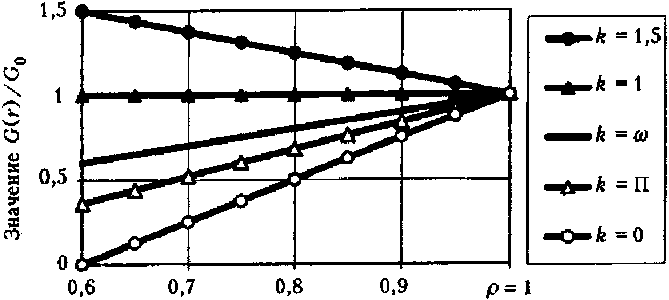
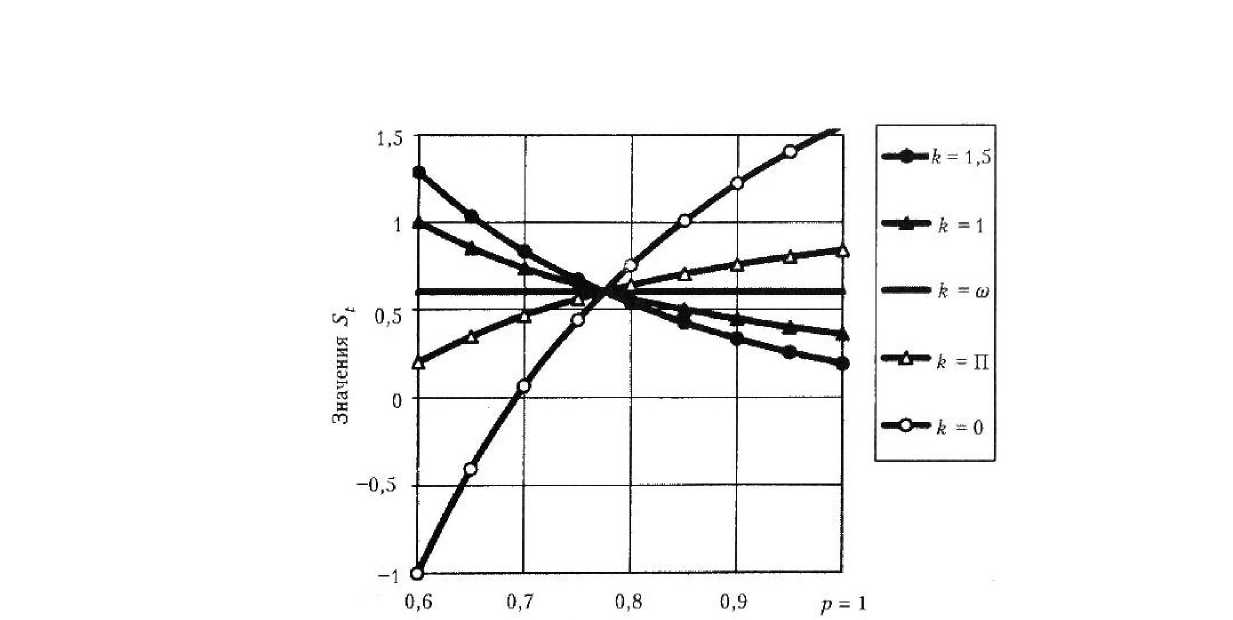
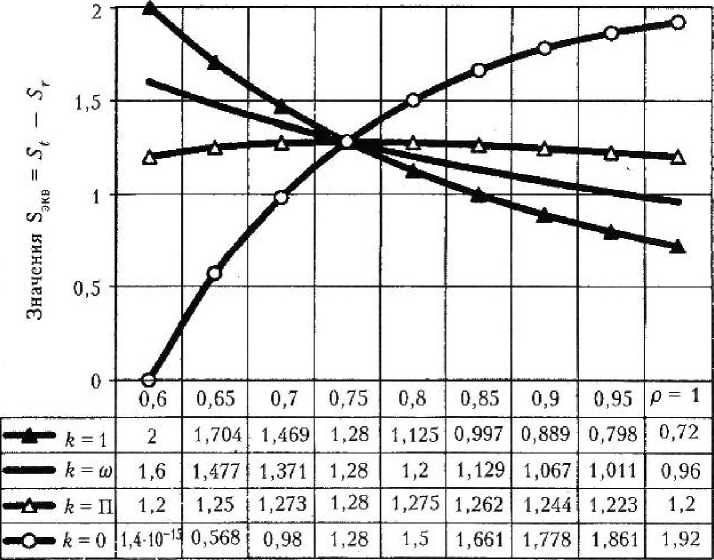
3(1-2v)’ 2 Положив v = 1/2 , получим К = « и G = £/3. Отсюда следует, что материал капилляра под действием давлений р и q, но при отсутствии объемных деформаций и сжимается, и растягивается в каждой своей точке. При этом за счет только деформаций чистого сдвига однородный капилляр расширяется или сужается [2; 4], а в его стенке появляются и радиальные, и окружные напряжения (положительные или отрицательные, в зависимости от знака и величины отношения давлений q/p = П). Становится очевидной неудач-ность термина «несжимаемый материал», вызывающего противоречивые ассоциации, Принимая сказанное во внимание, надо функцию £ (г), содержащуюся в выражениях (5), заменить функцией модуля сдвига G(r). Последнюю выберем, например, в виде степенной функции от безразмерной координаты с = т/Ь; G(7)^Goapm +5), (7) где л = (1-6) <к-о^ (1-^)’ (1-й^)' Go (8) Здесь G) — модуль сдвига в точках поверхности канала капилляра; Go — заданный модуль сдвига на наружной поверхности капилляра. Тогда с учетом формул (7), (8) интегральная функция, входящая в равенства (5), примет вид B(r) = /^dr = r3 _ Gop'2[2Apm - B(m -2)J 262(m-2) Значения этой функции на границах отрезка а < г > b следующие: R(^ _ ОйУ2АЮт -B(m-2)] П262(т-2) Ш)-^12"4, Б(т 2)1 (ю) 262(т-2) Удовлетворив условия (2), получим систему двух уравнений: — р = С2 + CjB(ti); -q = С2 + C^RU). (11) Разрешив систему (11) относительно коэффициентов, найдем: С _ Р"^ - 1 RU) - RU) ’ C2=-p-CARU). (12) Обратная подстановка в соотношения (5) выражений (7) и (12) дает окончательные формулы: для радиальных напряжений (в долях от порового давления р) Г R(r) RU) ) R(b) RU) i 1 R^ . RU) для тангенциальных (или окружных) напряжений (в тех же долях) 1 G(r) R(r) RU) г2RU) + RU) RU) 1 RU) RU) Еще раз уточним суть допущения о «несжимаемости» материала. Напряжения 5Г и St согласно равенствам (13) и (14) формально вроде зависят от величины отношения^/ р . В случае q /р - 1 напряжения суг = о^ ~ -р ~ const, что отвечает состоянию гидростатического сжатия, при котором отсутствуют деформации сдвига. Однако в «несжимаемом материале» наблюдается обратная ситуация: исключаются объемные, но сохраняются сдвиговые деформации. Поэтому из формул (13) и (14) нужно исключить не только величину q /р = 1, но и все другие значения q / р, кроме одного, вызывающего только сдвиги. Для однородных тел [2; 4] таким значением служит величина ^ = П. (15) Р Для численного анализа уравнений (13) — (15) рассмотрим случай линейной функции модуля сдвига, которую получим из выражения (7), положив т = 1 (рис. 2): GG)=G0(X1p + B1). (16) При этом согласно равенствам (8) ее коэффициенты будут равны: Из рис. 2 следует, что с увеличением координаты р при значениях к< 1 величина модуля G(r) возрастает, а при k > 1 — убывает. Значению к = 1 отвечает случай однородного материала, при этом формулы (13), (14) с учетом соотношений (15) — (17) дают классическое решение (задача Ляме). При условии т = 1 выражения, содержащиеся в квадратных скобках формул (13) и (14), также существенно упростятся и примут вид RU) _ 1 гл^ + В) №) ” П 2А^ВХ ’ Рис. 2. Линейная зависимость модуля сдвига от координаты р для капилляра с отношением ш = 0,6 R(r) _ 1 2Atp + Bj "№)-”#? 2^+Bj ’ jM. 2^ (lg) r^RQ/) p2 2Ht + Bx Для осмысливания результатов вычислений, производимых по формулам (13) — (15) при т = 1, целесообразно выделить случай, когда к = со . При этом коэффициенты Л1 = 1 и Г/ = 0. Их подстановка в уравнения (18) и (14) дает величину 1-69 S, = ^ = -1 + (1 - П) Р = 69= const. (19) Следовательно, при k = to окружные напряжения at = со р = const, то есть должны быть одинаковыми во всех точках капилляра. Результаты вычислений по формулам (13) —(15) с учетом выражений (18) представлены в виде эпюр напряжений на рис. 3, 4 (при к = 1 материал однороден). Из рассмотрения эпюр окружных напряжений 5t можно сделать вывод, что (см. рис. 3): 1) в случае й > 1 наиболее опасными будут всегда точки внутренней поверхности капилляра, так как при этом 5t больше соответствующих напряжений для однородного материала (к = 1); 2) с уменьшением к (величины модуля GP напряжения снижаются в точках внутренней поверхности капилляра, а в точках наружной поверхности, наоборот, растут; 3) при к = со = 0,6 эпюра St горизонтальна, то есть в соответствии с равенством (19) окружные напряжения at = со х р = const во всех точках капилляра; 4) эпюры любой пары St (при значениях к = псои к = со/п) взаимно симметричны относительно уровня напряжений при к = со, причем всегда S/к = со) = - S/k - nco) + S/k - —) . (20) 2 п (на рис. 3 таким двум эпюрам отвечает значение п = 0,6); 5) значения к = по и к = со/п, отвечающие паре взаимно симметричных эпюр, обладают свойством инверсии относительно значения к = со> 0, которое назовем степенью инверсивной неоднородности, так как (псо) (со/п) = со^\ 6) центр инверсии (к = 0) не имеет образа, поэтому и соответствующая эпюра St (к = 0) не имеет симметричной эпюры; 7) все эпюры пересекаются в одной точке (при р = 0,775). Это означает, что в капилляре существуют точки (цилиндрическая поверхность), в которых напряжения неизменны и равны ot = сор при любом значении к = G^Gq. Р и с. 3. Эпюры окружных напряжений <т(/ р в капиллярах композита (П = 36 %) с линейной неоднородностью (0 < k > 1,5) Р и с. 4, Эпюры эквивалентных напряжений (по координате р) для композита (П = 36 %) при исходных данных рис. 2, 3 Если оценивать прочность капиллярной ячейки пористого композита по 3-й теории прочности (теории Кулона), то целесообразно построить эпюры эквивалентных напряжений (см. рис. 4), вычисляемых по формуле Из анализа рис. 4 следует, что: 1) эпюры пересекаются в точке с координатой р = 0,75, в которой напряжения стэкв = S3KBp = 1,28р для всех значений к = G^Gq; 2) две в шоры 5ЭКС (при значениях к = оз/to = 1 и к = to to = И ) взаимно симметричны относительно эпюры со значением к, равным степени инверсии при соблюдении равенства ■^ЭКВ ^ = ^^ =2 [^ЭКВ^ = 1) + +-^экв^ = П)]; (22) 3) оптимальной (и равномерной) следует считать эпюру при значении к = П, что равносильно соотношению при котором 5'^х = 1,28р (в данном при мере). Очень важно, что равные напряжения (5ЭКВ = 1,2 р ) на наружной и внутренней поверхностях капилляра мало отличаются от величины 5™ВХ- Таким образом, при всех других равных условиях наибольшей прочностью будет обладать такой капиллярно-пористый композит (с линейной неоднородностью), для которого соблюдается условие (23): к - П. Опасные точки, к тому же, располагаются внутри стенки капилляра (при р-0,75). В заключение заметим, что приведенные выше рассуждения о прочности капиллярной ячейки справедливы и для неоднородной толстостенной трубы. 6 И Б Л И ОГРА Ф ИЧЕСКИЙ СПИ СО К 1. Андреев В. И. Некоторые задачи и методы механики неоднородных тел / В. И. Андреев. М. : АСВ, 2002. 288 с. 2. Светкина С. Н. Классификация деформаций ячейки капиллярно-пористого композита / С. Н. Светкина, А. С. Тюряхин // Актуальные вопросы строительства : материалы Всерос. науч.-техн, конф., посвящ. 40-летию строит, фак. Мордов. гос. ун-та. Саранск, 2002 Вып. 1. С. 342 — 346. 3. Светкина С. И. Упругие зависимости и эффективные модули жесткости капиллярно-пористых композитов / С. Н. Светкина, А. С. Тюряхин, В. Д. Черкасов // Проблемы строительного материаловедения : 1-е Соломатовские чтения : материалы Всерос. науч.-техн. конф. Саранск, 2002. С. 303 — 306. 4. Соломатов В. И. Макромеханика цилиндрической ячейки капиллярно-пористого композита / В. И. Солоиатов, В. Д. Черкасов, А. С. Тюряхин // Роль пауки и инноваций в развитии хозяйственного комплекса Республики Мордовия : материалы респ, науч.-пракг. конф. 27 — 28 марта 2001. Саранск, 2001. С. 283-291. 5. Черкасов В. Д. К определению пористости капиллярно-пористого композита / В. Д. Черкасов, А. С. Тюряхин, С. Н. Светкина // Современные технологии строительных материалов и конструкций : материалы Всерос. науч.-техн, конф., посвящ. 150-летию со дня рожд. акад. В. Г. Шухова. Саранск, 2003. С. 135-140 Поступила 05.04.05. НАПРЯЖЕННОЕ СОСТОЯНИЕ НАГРУЖЕННОГО КАСАТЕЛЬНОЙ НАГРУЗКОЙ НЕОДНОРОДНОГО ПОЛУПРОСТРАНСТВА, НЕ ОБЛАДАЮЩЕГО СПОСОБНОСТЬЮ ВОСПРИНИМАТЬ РАСТЯГИВАЮЩИЕ НАПРЯЖЕНИЯ Касательная нагрузка q равномерно распределена вдоль прямой липин (рис. 1). В случае плоской задачи она дей- ствует па протяжении достаточной длины. Модуль упругости полупространства с глубиной z возрастает или уменьшается.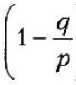
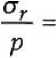
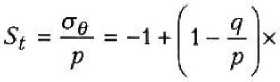
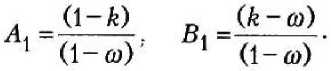
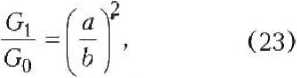
Список литературы Напряжения в капиллярах композита с неоднородностью непрерывного типа
- Андреев В. И. Некоторые задачи и методы механики неоднородных тел/В. И. Андреев. М.: АСВ, 2002. 288 с.
- Светкина С. Н. Классификация деформаций ячейки капиллярно-пористого композита/С. Н. Светкина, А. С. Тюряхин//Актуальные вопросы строительства: материалы Всерос. науч.-техн. конф., посвящ. 40-летию строит, фак. Мордов. гос. ун-та. Саранск, 2002. Вып. 1. С. 342 -346.
- Светкина С. Н. Упругие зависимости и эффективные модули жесткости капиллярно-пористых композитов/С. Н. Светкина, А. С. Тюряхин, В. Д. Черкасов//Проблемы строительного материаловедения: 1-е Соломатовские чтения: материалы Всерос. науч.-техн. конф. Саранск, 2002. С. 303 -306.
- Соломатов В. И. Макромеханика цилиндрической ячейки капиллярно-пористого композита/B. И. Соломатов, В. Д. Черкасов, А. С. Тюряхин//Роль науки и инноваций в развитии хозяйственного комплекса Республики Мордовия: материалы респ. науч.-практ. конф. 27 -28 марта 2001. Саранск, 2001. C. 283-291.
- Черкасов В. Д. К определению пористости капиллярно-пористого композита/В. Д. Черкасов, А. С. Тюряхин, С. Н. Светкина//Современные технологии строительных материалов и конструкций: материалы Всерос. науч.-техн. конф., посвящ. 150-летию со дня рожд. акад. В. Г. Шухова. Саранск, 2003. С. 135-140.


