Напряженно-деформированное состояние бесконечной плиты на деформируемом основании в зависимости от значений коэффициента пропорциональности продольных усилий

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 624.073.02                                     

Проектировщики в процессе профессиональной деятельности, встречаются с задачами расчета фундаментов зданий и сооружений на просадочных грунтах. Эти грунты особенно при эксплуатации зданий дают просадку (провал), т. е. неполный контакт конструкции фундаментов с грунтом [1, с. 71; 2, с. 150]. Неполный контакт также встречается при прохождении под зданиями всевозможных инженерных коммуникаций. Явление продольных усилий, приложенных в срединной плоскости встречается в практике проектирования при предварительном натяжении арматуры конструкций фундаментов.

Целью исследования является установление зависимости напряженно-деформированного состояния от величины коэффициента пропорциональности интенсивности продольных растягивающих и сжимающих усилий, приложенных в срединной плоскости бесконечной плиты и неполного контакта в виде двух траншей, расположенных симметрично вдоль оси Y (Рисунок 1).

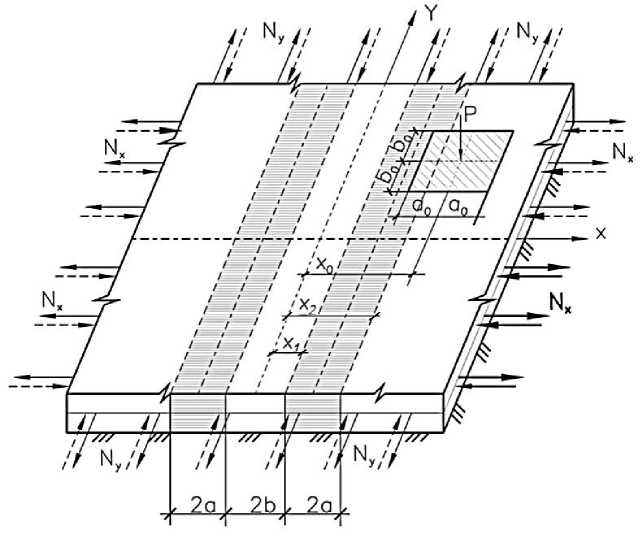
— участок неполного контакта

Рисунок 1. Расчетная схема бесконечной плиты на упругом основании с учетом влияния продольных усилий, расположенных в срединной плоскости плиты и неполного контакта в виде двух траншей, расположенных симметрично оси Y

Методы исследования

На основе ранее полученных авторами аналитических решений, которые получены методом обобщенных решений с использованием интегральных преобразований Фурье составлена программа в среде Delphi и вывод графиков осуществлялся с помощью программы AutoCAD [3, с. 10].

Результаты и обсуждение исследования.

Рассмотрим случай, когда внешняя нагрузка в центральной части и неполный контакт в виде двух траншей достаточно гибкой фундаментной плиты с грунтом расположен симметрично вдоль оси Y, шириной 2а=1,2 в безразмерных величинах достаточно гибкой фундаментной плиты. В этом случае плита может быть рассчитана по расчетной схеме бесконечной плиты.

В задаче также учтены продольные растягивающие и сжимающие усилия, приложенные в срединной плоскости бесконечной плиты [4, с. 27; 5, с 15; 6, с. 66].

Дифференциальное уравнение изгиба бесконечной плиты на Винклеровском упругом основании с учетом неполного контакта, в виде двух траншей, расположенных симметрично вдоль оси Y и продольные растягивающих и сжимающих усилий, приложенных в срединной плоскости плиты имеет вид:

D VV y (x, y ) + K _o [ 0 ( x - a ) + 0 ( x - b - 2 a ) ] y (x, y ) -

tf^ xy)

^x     д x ²

-

^{д 2 y (} x , y )

^у     д у ²

-

d ² ® ( x , y )

² N xy           = q o ⁽ x , y )

∂ x ∂ y

где D - цилиндрическая жесткость плиты, определяется по формуле:

n Eh3   . , _  „

D =------—; здесь v = — коэффициент Пуассона материала плиты;

12(1 -v2)6

h - толщина плиты; K o — коэффициент постели грунта;

0(x - a) и0(x - b - 2a) — функция Хевисайда, введение которой позволяет учесть отсутствие основания под частью плиты; 2а – ширина, а – полуширина траншеи;

л д2 ,52

А =    +    - оператор Лапласса

5x2d

NN — интенсивность растягивающих или сжимающих продольных усилий, приложенных в срединной плоскости бесконечной плиты вдоль осей Х и Y, они считаются положительными при растяжении и отрицательными при сжатии; N — интенсивность касательных усилий, приложенных в срединной плоскости плиты;

В связи с малой интенсивностью N_xy , не снижая общности задачи принимаем равным нулю. С учетом формулы (2), выражение (1) запишем в виде:

(S2^ + S2^)(^^xy) + S2^) + K0 [0(x- a) + 0(x -b - 2a)]a(x,y) -дx        дy        дx        дy д2у( x, y)      д 2y( x, y)      ,    .

^- N x         ^- N y          = q 0⁽ x , y )

д x            д y

Раскрыв скобки получим:

д ² y ( x , y )     д ⁴ © ( x , y Y ,д⁴ у ( x , y )

—+ 2 _я 2 )(— + K 0 [ 0 ( x - a ) + 0 ( x - b - 2 a ) ] y ( x , y ) -

• д x         д x д y       o y

д² y ( x , y )    ... д² y ( x , y )      .    .

• ^- N x   \   ^- N y    o 2   = q o ( x , y )

д x           д y

В ранее проведенных авторами исследованиях рассматривались задачи изгиба бесконечной плиты с учетом неполного контакта с основанием в виде двух траншей, расположенных симметрично относительно оси Y в центральной части плиты. При этом также учитывались продольные усилия, приложенные в срединной плоскости бесконечной плиты [7, с. 256]. В этом случае максимальное значение прогиба и изгибающего момента в центре бесконечной плиты на винклеровском упругом основании без учета неполного контакта и влияния продольных усилий равны. На основании ранее полученных результатов исследований с учетом неполного контакта с основанием, в виде двух траншей с полушириной b=0,1; а=0,6 без учета продольных усилий минимальное значение прогиба и изгибающего момента равны [8, с. 19; 9, с. 137].

о (0,0)=0,1655; Mx(0,001)= - 0,2001

^ (0,0)=0,1249 и M^ (0,001)= - 0,2910 в безразмерных величинах.

А результаты с одновременным учетом неполного контакта бесконечной плиты с основанием в виде двух траншей с полушириной а=0,6; b=0,1 и продольных растягивающих усилий по осям X и Y значение максимального прогиба а значения максимального прогиба & P = 0,1266 , а максимального изгибающего момента M Р_х = - 0.1587 , а максимального прогиба с учетом сжимающих продольных усилий по осям X и Y и тех же факторов а= 0,6; b=0,1; ^ ж =0,2369; M сж =- 0,1481

В данной статье проводимое исследование напряженно-деформированного состояния бесконечной плиты на винклеровском упругом основании при одновременном учете неполного контакта с основанием в виде двух траншей полушириной а= 0,6; b=0,1, расположенных симметрично вдоль оси Y и продольных и растягивающих усилий, приложенных в срединной плоскости плиты, в зависимости от величины коэффициента пропорциональности α интенсивности продольных усилий, меняющаяся от ∝ =±0,1 до ∝ =±0,5. Исследование проведено при интенсивности продольных усилий N= 200 т/м. В Таблице 1 приведены результаты расчета с учетом влияния продольных растягивающих и сжимающих усилий в двух направлениях по осям X и Y и неполного контакта с основанием в виде двух траншей, расположенных симметрично вдоль оси Y, при а= 0,6; b=0,1 и ∝ n =±0,5.

Таблица 1

Результаты расчета бесконечной плиты на винклеровском упругом основании с учетом неполного контакта с основанием в виде двух траншей, расположенных вдоль оси Y и влияние продольных растягивающих и сжимающих усилий в двух направлениях по осям X и Y, при полуширине а=0,6; b=0,1 и коэффициента пропорциональности меняющимся в пределах ∝ n =0,1÷0,5

∝ n	По осям X и Y              По осям X и Y             Интенсивность ^ р (0.0)     M р х (0.01)      ^ сж (0.0)    M ж (0.01)      продольных усилий, т/м
±0,1	0,1266        -0,1587        0,2369        -0,1481                200
±0,2	0,1194        -0,1619        0,2551        -0,1452                200
±0,3	0,1134        -0,1635        0,2781        -0,1409                200
±0,4	0,1069        -0,1668        0,3059        -0,1305                200
±0,5	0,1009        -0,1847        0,3371        -0,1296                200

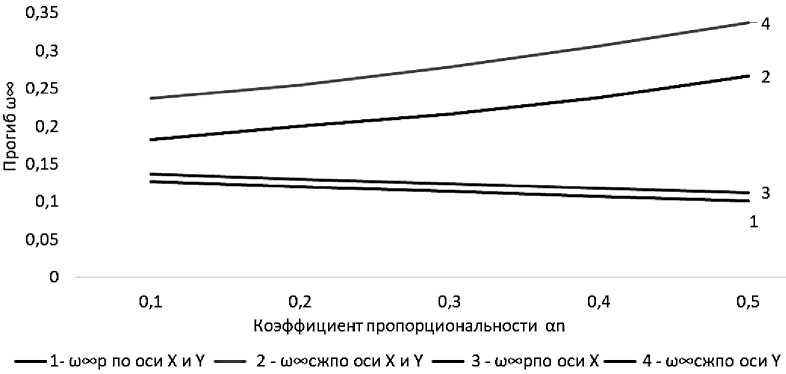
Рисунок 2. Эпюры прогибов ω(x,y) в бесконечной плите на винклеровском упругом основании с учетом неполного контакта с основанием в виде двух траншей, расположенных вдоль оси Y и влияние продольных растягивающих и сжимающих усилий в двух направлениях по осям X и Y, при полуширине а=0,6; b=0,1 и коэффициента пропорциональности меняющимся в пределах ∝ n =0,1÷0,5

Таблица 2

Результаты расчета бесконечной плиты на винклеровском упругом основании с учетом неполного контакта с основанием в виде двух траншей, расположенных симметрично вдоль оси Y и влиянием продольных растягивающих и сжимающих усилий, приложенных в срединной плоскости плиты, только по оси X, при полуширине а= 0,6; b=0,1

и коэффициента пропорциональности меняющимся в пределах ∝ n =0,1÷0,5

∝ n	По оси X		По оси Y		Интенсивность Продольных усилий, т/м
	^ р (0.0)	мж (0.01)	-> сж (0.0)	M ж (0.01)
±0,1	0,1364	-0,1714	0,1819	-0,1255	200
±0,2	0,1299	-0,1748	0,2003	-0,1230	200
±0,3	0,1237	-0,1765	0,2163	-0,1194	200
±0,4	0,1179	-0,1801	0,2379	-0,1148	200
±0,5	0,1123	-0,1819	0,2665	-0,1093	200

----1- М“хр(0,01) по осям X и Y ----2- М”хок(0,01) по осям X и Y

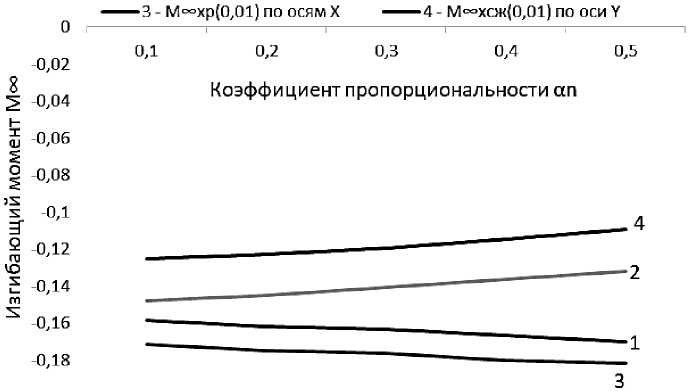
Рисунок 3. Эпюры изгибающих моментов Мx(x,y) в бесконечной плите на винклеровском упругом основании с учетом неполного контакта с основанием в виде двух траншей, расположенных вдоль оси Y и влияние продольных растягивающих и сжимающих усилий в двух направлениях по осям X и Y, при полуширине а=0,6; b=0,1 и коэффициента пропорциональности меняющимся в пределах ∝n=0,1÷0,5

Выводы по Таблице 1: Анализ результатов расчета бесконечной плиты на винклеровском упругом основании с одновременным учетом неполного контакта с основанием в виде двух траншей, расположенных вдоль оси Y и полушириной a=0,6 и b=0.1 и влиянием продольных растягивающих усилий, приложенных в срединной плоскости плиты по осям X и Y , действующих в срединной плоскости плиты (Рисунок 2) показывает, что максимальный прогиб в центре плиты ω ∞ (0,0) уменьшается с увеличением коэффициента пропорциональности интенсивности продольных растягивающих усилий ∝ n . В частности, при ∝ n =±0.1 максимальный прогиб в центре плиты ω ^р (0.0) = 0.1266, а при ∝ n =±0.5 он равен ω ^р (0.0) = 0.1009, т. е. в 1.26 раза меньше. Изгибающий момент увеличивается с увеличением ∝ n , в частности при ∝ n =±0.1, значение M ^р (0.01) = - 0,1587, то при ∝ n =±0.5, он равен M ^р (0.01) = - 0,1847, т. е. увеличивается в 1,1 раза.

В случае одновременного учета неполного контакта с основанием, в виде двух траншей, расположенных симметрично вдоль оси Y и полушириной a=0,6 и b=0.1 и влиянием продольных растягивающих усилий, приложенных в срединной плоскости плиты по осям X и Y (рис. 1), результаты показывают, что максимальный прогиб в центре плиты увеличивается с увеличением коэффициента пропорциональности интенсивности продольных растягивающих усилий ∝ n .

При ∝ n = -0,1 максимальный прогиб в центре плиты ω ^сж (0.0) = 0.2329, а при ∝ n = -0,5, прогиб ω ^сж (0.0) = 0.3371, т. е. в 1,43 раза больше. Изгибающий момент уменьшается при ∝ n =-0,1, он равен M ^сж (0.01) = - 0,1481, а при ∝ n = -0,5, он равен M ^сж (0.01) = - 0,1296, т. е. уменьшается в 1,14 раза.

Выводы по Таблице 2: Анализ результатов расчета бесконечной плиты на винклеровском упругом основании с одновременным учетом неполного контакта с основанием в виде двух траншей, расположенных вдоль оси Y и полушириной a=0,6 и b=0,1 и влиянием продольных растягивающих усилий, приложенных в срединной плоскости плиты только по оси X (Рисунок 3) показывает, что в центре плиты максимальный прогиб также уменьшается, с увеличением коэффициента пропорциональности интенсивности продольных растягивающих усилий ∝ n . В частности, при ∝ n =+0,1, максимальный прогиб равен ω ^р (0.0) = 0.1364, а при ∝ n =+0,5, он равен ω ^р (0.0) = 0.1123, т. е. в 1,23 раза меньше. Изгибающий момент M ^р (0.01), при ∝ n =+0,1 равен M ^р (0.01) = - 0,1714, а при ∝ n =+0,5, он равен M ^р (0.01) = - 0,1819, т. е. в 1,06 раза больше.

С учетом сжимающих продольных усилий только по оси X, максимальный прогиб в центре плиты увеличивается, в частности при ∝ n =-0,1, максимальный прогиб равен ω ^сж (0.0) = 0.1890, а при ∝ n =-0,5, он равен ω ^сж (0.0) = 0.2665, т. е. в 1,41 раза больше. Изгибающий момент уменьшается с увеличением ∝ n , в частности при ∝ n =-0,1, максимальный изгибающий момент равен M ^сж (0.01) = - 0,1255, а при ∝ n =-0,5, он равен M ^сж (0.01) = - 0,1093 , т. е. в 1,15 раза меньше.