Напряженно-деформированное состояние при безоправочном волочении тонкостенных труб с подпором

кольцевых элементов одинаковой длины l0. В процессе волочения исходные элементы при протягивании через профилированный канал волоки под действием осевых сил Рв и Q деформируются и занимают положения, определяемые радиусами R1, R2, … , Ri, … , RN. Соответственно длина образующих и толщины стенок элементов при R1, R2, … , Ri, … , RNпринимают значения l1, l2, … , li, … , lN и S1, S2, … , Si, … , SN. Число элементов должно быть достаточным для того, чтобы в пределах каждого элемента процесс деформирова- ния считался монотонным.

В качестве параметров деформированного состояния, описывающих бесконечно малые приращения деформаций, для i-го элемента использовали логарифмические деформации:

5                 I

"i-l            Лг-1            4-1

связанные между собой условием постоянства объема:

и интенсивность бесконечно малых приращений деформаций:

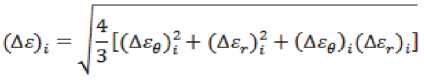
. (1)

Конечные деформации е l , е₆ , е r для каждого i-го элемента находят, суммируя бесконечно малые приращения деформации i-го элемента и конечные деформации (i-1)-го элемента, т. е.

<ЛХ = teiX-i + (Д^Х ; ОД = ОД-i + (Д^£Д Wi = (^£r)i-l + (^^ErX UDi = (^£i)i-i +' (^1)1 ■

Printed with pdfFactory Pro trial version - purchase at

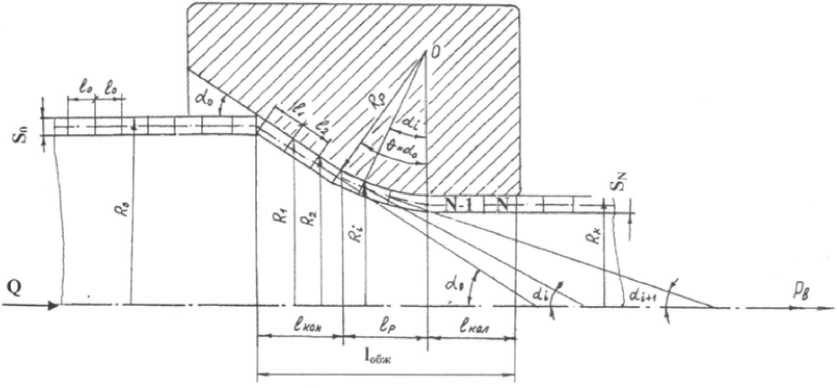
Рис. 1. Волочение тонкостенной трубы

Компоненты напряженного состояния с т l и о_в определяют по известным компонентам деформированного состояния из уравнений теории пластического течения:

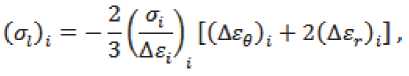
На цилиндрическом участке считаем, что R l = то, R _О = R_к, где R_к - конечный радиус готовой трубы.

Уравнения равновесия элементов в направлении касательной к меридиану на коническом, радиусном и цилиндрическом участках канала волоки соответственно следующие:

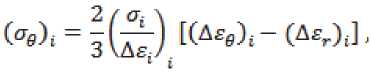
— (atRS) -a9S-

^PR sina

= 0 ,

где с i — интенсивность напряжений.

Интенсивность напряжений для i-го элемента находят из закона упрочнения металла заготовки, например, заданного в виде степенного ряда:

d

— (ajRS) — R^OgSsinQ + (iPR) = 0 , 0,6

dl

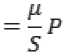
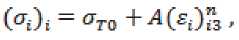
где с т — предел текучести материала заготовки при входе в волоку,

А и n – коэффициенты аппроксимации ди-

аграммы упрочнения.

Контактное давление Рi для i-го элемента можно получить из уравнения равновесия сил в

направлении нормали к меридиану:

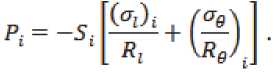
Здесь д - коэффициент внешнего трения. Представив эти формулы в конечных разностях и проинтегрировав методом трапеций [3], окончательно будем иметь:

на коническом участке

,    .    ,    . R, + R_i+i Г/ pPR\

(_O1RS)_t - (^Й5)_Н1 = *   ¹⁺¹ L₆5 + — +

2*        . x siTict/ ^

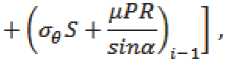
Здесь Rl – радиус кривизны меридиального сечения;

R _в - радиус кривизны сечения трубы конической поверхностью, перпендикулярной дуге меридиана.

На коническом участке принимаем, что R 1 = ^, (R _О )_i=R i /cos а , на радиусном R l определяется геометрией радиусного перехода (R_и)_i=R_i/cos О (R i - радиус окружности в сечении плоскостью перпендикулярной оси волочения; а , О - углы между касательной к меридиану и осью волочения на коническом и радиусном участках соответственно).

на радиусном участке

6+6

(ojRS^ - (ojRS)^ = ^^[(a_gSsinS + цРР\ +

на цилиндрическом участке

Таким образом, для любого элемента в кана-

ле волоки получаем замкнутую систему уравне-

ний для определения неизвестных R i , S i , l i , e₀ i , e_l i , e ri , (e i ) I , (a i ) I , a l , a₀, P i . Для конического участка система включает уравнения (1) – (8), для радиусного – (1) – (7) и (9), на цилиндрическом участке используется только уравнение (10). В связи с тем, что деформация трубной заготовки является осесимметричной, параметры напряженно-деформированного состояния – только функция одной независимой переменной либо радиуса R, либо угла Q . Поэтому решение системы (1) - (9) в представленной последовательности сводится к решению трансцендентного уравнения (8) или (9) в функции независимой переменной.

Процесс вычисления параметров напряженно-деформированного состояния начинается на коническом участке со значения i=1. При этом для кольцевого элемента, расположенного до входа в очаг деформации, считаются известными все параметры напряженно-деформированного состояния. Для ненагруженного элемента обычно принимают = = = = е =0, ст, = P = 0, l r У             У a l=Q/F0, где F0 - площадь поперечного сечения заготовки на входе в волоку.

Так как геометрия первого элемента в процессе волочения неизвестна, то предполагаем, что изменение длины образующей l1 будет происходить на отрезке [0,95 l0, 1,05 l0]. Это дает воз-

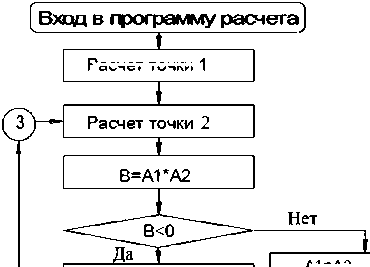
Расчет точки 1

R3=R2

L3=L2

L2= (L1+L2) /2

R2= (R1+R2) /2

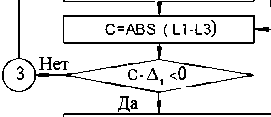
Расчет истинных деформаций и напряжений

A1=A2

R1=R2

L1-L2

L2= (L2+L3) /2

R2= ( R2+R3) /2

Сохранение результатов расчета

Выход из программы расчета

Рис. 2. Алгоритм расчета параметров напряженно-деформированного состояния в кольцевом элементе можность при численном решении на ЭВМ приведенной системы уравнений воспользоваться методом дихотомии [3]. Расчет действительного значения R1, определяющего точную геометрию первого элемента, проводится с точностью д 1: |Rk+11 - Rk1| < Д 1, где k+1 и k - номера приближений для независимой переменной. Другие параметры элемента находят из геометрических соотношений Si=(S0l0R0)/(R1l1), l1=(R0-R1)/sinа. По точным значениям параметров геометрии первого элемента по соотношению (1), (3) – (5) определяют истинные значения деформаций и напряжений (рис. 2), критерием правильности их выбора служит обращение уравнения равновесия (8) в тождество. Расчет параметров напряженно-деформированного состояния для последующих элементов 2, 3, … , i, … , N проводится в аналогичной последовательности за исключением того, что на радиусном участке в качестве независимой переменной используется угол Q, а на цилиндрическом участке находят только а1.

После того, как будет определено напряженно-деформированное состояние во всех элементах канала волоки, процесс вычислений не заканчивается. Для достижения заданной точности расчета усилия волочения Д₂ нужно вести те же самые вычисления, увеличив число ранее заданных кольцевых элементов. Требуемая точность д 2 достигается при выполнении неравенства (Р ^т+1 _в - Р ^т _в) < д 2 , где m+1 и m - номера приближений по усилию волочения, Р = ст 1 N ( л (2R -S_N)S_N), рис. 3.

Результаты расчета параметров напряженно-деформированного состояния на ЭВМ при волочении медных труб из сплава М3 с различным подпором представлены на рис. 4. В процессе вычислений принято R₀=16 мм, S₀=1 мм, l₀=0,5 мм, l а =5 мм, R =1 мм, а =12е, R =13 мм, a =75+58 е _L 0,4² , ^ =0,12, д 1 =10 ^-4 мм, Д 2 =50 Н.

Из анализа графиков следует, что по мере продвижения металла трубы вдоль волочильного канала длиной l0 меридиональное напряжение возрастает, достигая своего максимального значения на выходе из канала волоки. Меридио-

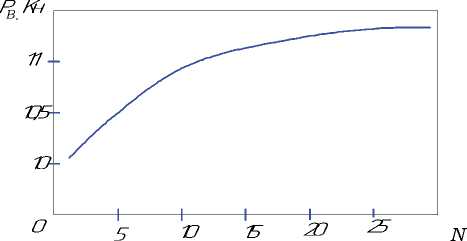
Рис. 3. Влияние числа кольцевых элементов N на изменение усилия волочения Р_в

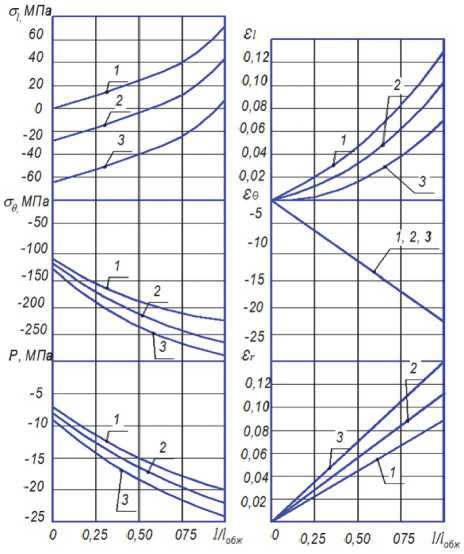
Рис. 4. Распределение параметров напряженно-деформированного состояния по длине канала волоки:

1 – q=0 МПа, 2 – q=30 МПа, 3 – q=70 МПа нальное напряжение больше при волочении тонкостенной трубы без подпора. Чем больше подпор, тем меньше уl, и соответственно больше степень деформации заготовки за проход. При под- поре q=Q/F0=70 МПа, осевое напряжение близко к нулю. По этой схеме реализуется процесс осадки трубы вдавливанием в волоку.

Окружные сжимающие напряжения и контактное давление Р распределены по длине канала волоки по нелинейному закону, возрастая по абсолютной величине к выходу из канала волоки. Подпор со стороны входа заготовки в волоку вызывает увеличение о_в и Р Чем больше подпор, тем выше рост о_в и Р

Величина тангенциальных деформаций не зависит от величины подпора. Подпор существенно влияет на величину меридиональных и радиальных деформаций е l и е r . Чем больше подпор, тем больше утолщаются стенки трубы, а длина полученной трубы меньше, чем при традиционном волочении без осевого подпора.

Использование предлагаемой методики позволяет моделировать реальные процессы безоп-равочного волочения тонкостенных труб на непрерывных станах и может быть полезным при создании САПР технологических процессов для выбора оптимальных режимов волочения.