Напряженно-деформированное состояние при пластическом деформировании композиционных низкотемпературных сверхпроводников

Для создания сверхпроводящих магнитных систем (СМС) наиболее широко используются низкотемпературные сверхпроводники (НТСП) 2-го рода.

Важнейшими характеристиками НТСП являются критическая температура T c , критическое магнитное поле H c и также критическая плотность тока j_c . Указанные критические параметры являются структурно чувствительными и существенно изменяются в результате термомеханической обработки.

Теория НТСП 2-го рода основана на модели пиннинга (от английского pinning - пришпиливание) - проникновении магнитного поля внутрь сверхпроводника в виде квантованных вихрей, закрепляющихся на дефектах объемной нанокристаллической структуры, называемых центрами пиннинга . Создание такой структуры обеспечивается конструкцией НТСП и технологией их изготовления.

Наиболее широко применяются НТСП на основе сплава NbTi и интерметаллического соединения Nb3Sn.

Основными центрами пиннинга в сплавах NbTi являются мелко дисперсные частицы a-Ti, выделяющиеся из Р-твердого раствора по границам деформационных микрополос в местах скопления дислокаций. Такая структура может быть получена после очень большой степени деформации сначала в горячем, а затем в холодном состоянии.

Более высокими критическими параметрами обладают сверхпроводники на основе интерметаллического соединения Nb3Sn. Соединение Nb3Sn чрезвычайно хрупкое, поэтому для изготовления длинномерных сверхпроводников применяется метод селективной твердофазной диффузии - «бронзовая технология». Идея метода заключается в совместном многократном деформировании сборки заданной структуры, состоящей из коаксиальных волокон ниобия и оловянистой бронзы для получения длинномерных композиционных заготовок с заданной структурой распределения по сечению ниобиевых волокон диаметром 5-130 мкм в проводнике диаметром 0,1-1,0 мм с общим числом порядка ~101^104 . По окончании деформационной обработки в результа-

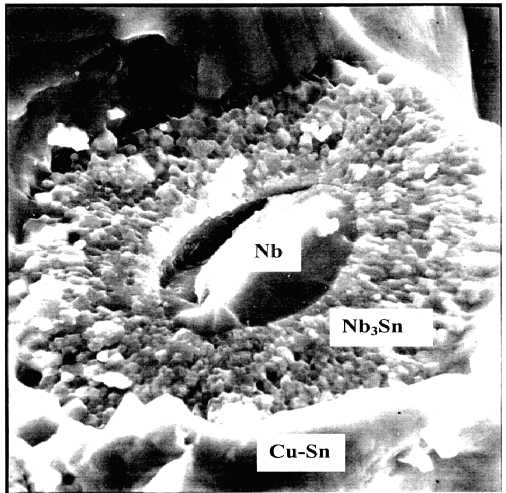
Рис. 1. Поперечное сечение волокна сверхпроводника после диффузионного отжига

те диффузионного отжига при температуре 700-750 ° С образуется соединение Nb3Sn (рис. 1) с размером зерен менее 100 нм.

В проводниках на основе ин-терметаллида Nb3Sn содержание сверхпроводящей фазы определяется конструкцией проводника, диаметром волокон и, ограниченно, содержанием олова в бронзе и соотношением олова и ниобия в композите. Допустимое содержание олова в бронзе ограничивается пределом его растворимости в меди в твердом состоянии - 13-

14 мас. %. Такие бронзы имеют низкую пластичность и после деформации на 45-50 % требуется отжиг заготовки при 500-550 °С.

Для получения высоких значений критических характеристик проводники для СМС на основе сверхпроводников 2-го рода изготав- ливаются в виде комбинированных композитов, имеющих высокую однородность свойств по длине (1-30 км).

В настоящее время в РФ в рамках проекта ITER (международный термоядерный исследовательский реактор) разворачивается масштабное производство НТСП для СМС. В перспективе производимые НТСП планируется применять в электротехнике, приборостроении, медицине.

При производстве проводников на основе НТСП наиболее длительным и ответственным является волочильный передел, связанный с многократным холодным пластическим деформированием композиционной заготовки с диаметра 60-70 мм на диаметр 0,1-1,0 мм. На этом этапе изготовления необходимо обеспечить безобрывность процесса и получение заданной плотности микродефектов, чтобы обеспечить образование центров пиннинга в случае сверхпроводников на основе сплава NbTi или исключить разрушение заготовки на промежуточных стадиях деформирования при производстве сверхпроводников по «бронзовой технологии».

Для решения указанной задачи необходимо проектировать технологический процесс с учетом накопления поврежденности (дефектности) структуры сверхпроводниковой композиционной заготовки на каждом этапе пластического деформирования.

Для проектирования технологии многоэтапного пластического деформирования длинномерных композиционных НТСП предлагается методика расчёта напряженно-деформированного состояния заготовки НТСП в очаге пластической деформации.

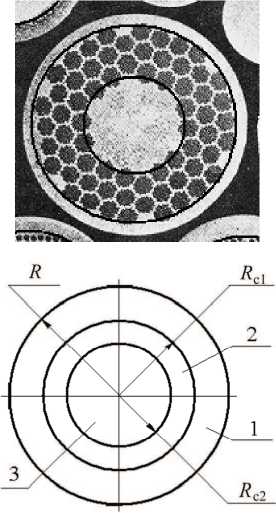
Различные конструкции сверхпроводников на основе сплавов NbTi и соединения Nb3Sn представлены на рис. 2.

Сечение проводника для СМС представляет собой сложный геометрический объект и может быть представлено как трансверсальноизотропный двух- или трехслойный композит (би- или триметалл), наружный слой которого состоит из медной токостабилизирующей оболочки, а промежуточный слой или сердечник являются композитом, состоящим из волокон NbTi или ниобия, размещенных в медной или бронзовой матрице, эффективные механические характеристики которого определяются механическими характеристиками металла волокон и металла матрицы и их процентным отношением в сечении проводника (см. рис. 2).

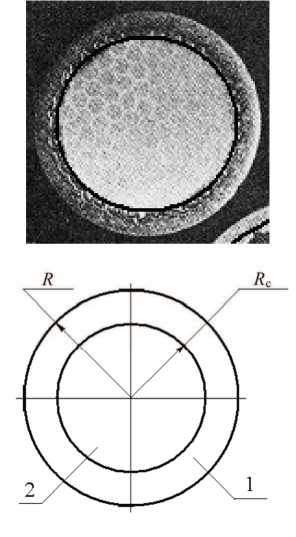
Рис. 2. Схематизация конструкций сверхпроводников в виде би- и триметалла: 1 - оболочка; 2 - промежуточный слой; 3 - сердечник; R - радиус проводника; R _С1 - наружный радиус промежуточного слоя; R _с2 - радиус сердечника

Определим деформированное состояние заготовки, принимая, что процесс деформирования монометаллических и композиционных заготовок подчиняется общим закономерностям, а материал заготовки жестко-пластический.

Определим кинематически возможное поле скоростей в очаге деформации (рис. 3). Угол наклона линий тока 9 определится следующим образом:

tg 6 =

dr _            r • tg a • tg ф- tg ( a + p )

dx' r • tg a • tg (a + p) - tg a - tg ф + tg (a + p) tg ф где r0 I R0 = r IR = r ; r - относительный радиус линии тока; r и r0 -текущий и начальный радиус линии тока; R = R0 + x • tg a и R0 - текущий и начальный радиус заготовки в канале волоки; p = arctg (fn) -угол трения; tg ф = r • sin (a + p) I 1 - r 2 • sin2 (a + p) ; a - угол наклона образующей канала волоки.

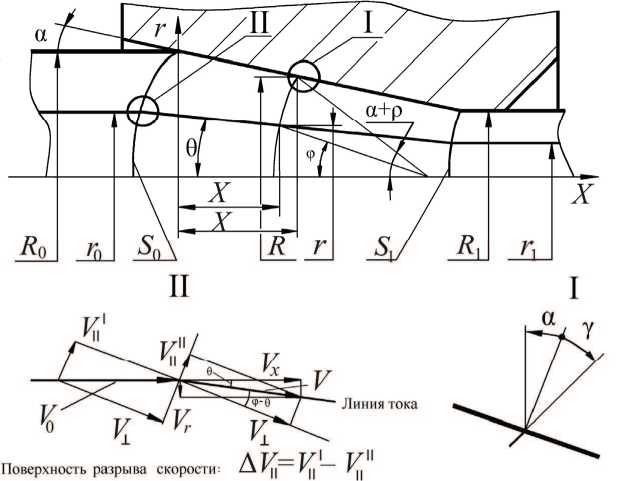
Рис. 3. Кинематически возможное поле скоростей при волочении заготовки

Определим компоненты тензора скоростей деформаций ^ X , ^ r , ^ ф .

Из рис. 3 определим -_r = - -_X - tg 6 . Подставляя полученные выражения в уравнение неразрывности для осесимметричного течения и учитывая граничное условие -_X^_X = 0 = —_X 0 , получим

V

2 -к tg 6 = 0;

r

5 -x r Ъф ; Ъх ^r т)ф 5

- X = - X о ( R о / R ) ²;

^X = 2-хо-0-tg6'; ^r =^ R3

ф

^- x ° ₁ R 2 tg 6' ;

R ³

Л rx 2

1 ^5 V x

v 5 r

)5 x J

^^^^^^^в

2 -^ r -tg’- e' , R ³

где tg 6' = ^g⁶ . r

Определим интенсивность скоростей деформации сдвига и степень деформации частиц вдоль линии тока:

H =    V ( 5 . -5 , )² + ( 5 , -5 , )² + ( 5 ф -5 . )² + 3/2 _П 2 х ;

T а =

Hdt = 74 + (4/3) • tg² 0 • ln ( R_o / R ) ,

V3 J где dt = dx / Vx; T - время движения частицы металла вдоль линии тока.

На границах очага деформации S0 и S 1, являющихся поверхно стями разрыва скорости, частицы металла получают приращение степени деформации

Аа = (1/V3) •[А V _и|/ V ₁ ,                        (3)

где VL - составляющая скорости, перпендикулярная поверхности разрыва; А VII - разность составляющих скорости, параллельных поверх ности разрыва.

Из рис. 3 следует: справа от поверхности S 0 - V " = V_v- tg ( ф - 0 ) = V ₀ • cos ф^ tg ( ф - 0 ), слева - V ₁ = V 0 • cos ф ; V i = V ₀ • sin ф . Подставляя полученные соотношения в формулу (3), получим

АЕ= tg ф-tg(^-0) =    l+tgSp tg 0.

V 3         V3 • (1 + tg ф tg 0 )

На границе S 1 приращение степени деформации определяется аналогично. Суммарная степень деформации частицы вдоль линии тока определится следующим образом:

^£ !

= 2 Аа + а =

2 •(1 + tg ф)   tg 0+ /4 + 4tg2 0 • ln f R0

V3 • (1 + tg ф^ tg 0 )       v ³          ( ^R 1 )

На практике процесс волочения осуществляется при а< 10°, fn <0,1 и Rо/R1 < 1,3, поэтому можно принять tg 0 « r • tg а ;

1+ tg2 ф _ 1

1 + tg ф^ tg 0

откуда

£

1 - 73r" tgа B+2ln

(R о)

k R1)

Полученное соотношение верно для очага деформации с плоскими границами [1]. Условие плоских границ будем использовать при определении напряженного состояния заготовки в очаге деформации (рис. 4).

При анализе процесса волочения слоистых композиционных заготовок используем усредненные по толщине каждого слоя, ограниченного волокнами с координатами r i - r i R и r _i+1 - r i _{+ 1} R , значения степени деформации:

^£ Z cp ^-

r i + 1

2k J £zr dr ri4

k ( r i + 1 - r ²)   sVs

_ 1 - R i ³ r^{i + 1}1 - R 2

С tg а в + 2ln -° , k Ri)

^гд^{е R} i = r / ri + 1 .

Для определения напряженного состояния примем следующие допущения:

• 1.    Отношение толщины слоев элементов композиционной заготовки постоянно, R i — R i / R — const, где R i , R - наружный радиус i -го слоя и заготовки в очаге деформации.

• 2.    Напряжения распределены равномерно по сечению каждого слоя и являются главными (подход Закса).

  

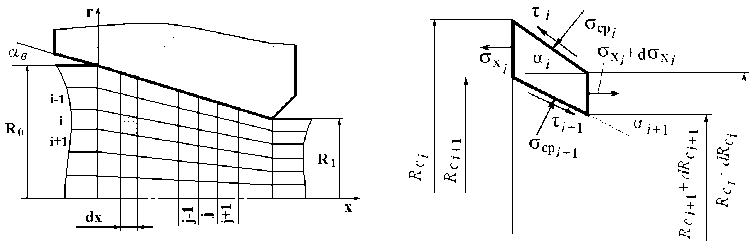
  Рис. 4. Схема очага деформации

  
  

• 3.    Из равенства £ _r = £ _ф следует равенство ст _r = ст _ф .

• 4.    Касательные напряжения на поверхности контакта заготовки и волоки определяются законом Кулона-Амонтона: т _тр = f_n -ст _n 1 .

• 5.    На границах слоев касательные напряжения определяются [2] следующим образом

• 6.    Для исключения разрыва компонент тензора напряжений примем, что на границе слоев существует тонкий промежуточный слой, в пределах которого нормальные напряжения изменяются по линейному закону, а непосредственно на границах слоя нормальные напряжения определяются выражениями

  „      ^ст ni - 1 ^+ст ni . „

  ^ст cpi = —2—; ^ст

  
  

Рис. 5. Схема напряженного состояния элемента слоя заготовки

Так как a< 10°, то принимаем на поверхностях контакта слоев стr «стn   и используем упрощенное условие пластичности стxi + стni = стsi, где стхi и стni - продольные и нормальные напряжения в i-м слое заготовки; ст si - сопротивление деформированию металла i- го слоя заготовки.

T i fn ' ст n 1 ' Ri , где ст n 1 - нормальные напряжения на контакте заготовки и инструмента.

.      = ст ni +ст ni+1

cpi+1          2       , где стni-1, стni, стni+1 - нормальные напряжения в соседних слоях.

Выделим элемент произвольного слоя заготовки в очаге деформации (рис. 5) (на рис. 4 элемент заштрихован).

Дифференциальное уравнение равновесия выделенного элемента слоя с учетом принятых допущений имеет вид dст xi dx

^^^^H

tg a , ст +ст xi

xi - 1

tg a 1

R 1 - R 2

^^^^H

^ст xi + 1

tg a

R 1 - R

+

2 f n

+ ст x1 R

^^^^H

tg a стя

s 1 _R

(                     ^

pi- 2 a + p i-1 p«

V            1 Rci J

= 0,

где R_ci = R i _{+ 1}/ R i ; a = f_n / tg a ; p i = ст si I ст s 1 - коэффициент неоднородности пластических свойств; ст s 1 , ст si - сопротивление деформации металла наружного и i -го слоя соответственно.

После перехода к безразмерным параметрам уравнение (6) принимает вид

R ( d ст i I dx ) + ст i • a i + ст 1 • a ₂ i + ст i _{- 1} • a ₃ i + ст i _{+ 1} ■ a ₄ i + a ₅ i = 0,      (7)

где          ^ст i = ^ст xi ^{1 ст} si ;

L = ( R о - R JItg a ;

x = x IL ; R = RIR ₀ = (1 - x ■ tg a ) I R ₀;

n,-i A n A ai i = -A; a2, =2a • A1 n i; aз i =—; a4i =—r^;

i                  n ^{1 - R 2} n ^{1 - R 2}

a 5 i = A

^{2 a} , n i - 1 ^-n i + 1 n i n i • (1 ^{- R} ei )

; R = 1 - x ■ A ; A = 1 - R 1 1 R ₀.

Для n-слойной композиционной заготовки (i = 1, n) после подста новки соответствующих параметров можно получить систему неоднородных дифференциальных уравнений первого порядка с переменными коэффициентами, решение которой позволяет определить продольные напряжения в каждом слое. Нормальные напряжения определяются из условий пластичности (10) для соответствующего слоя, а касательные напряжения на границах слоев - из уравнения (12).

Использование уравнения (7) позволило получить расчетные соотношения для определения напряжений в слоях наиболее распространенных типов слоистых композиционных заготовок - би- и триметаллов.

Биметаллические заготовки ст1 = ст1I ст S 1 =пст 2 + Дст;(8)

ст2 = ст2 I ст „ = C + (ст 2 - C - C2) R 2а + C2 R 2(B-1); 2    2 S 2    1    q 2   122

Дст = (1 - n )[ B I ( в - 1)] [ 1 - R ²⁽ B ^{- 1)} ] + ( ст q 1 -пст q 2 ) R ²⁽ B ^{- 1)} ;

С 1 = (1I a n ) [ 1 + 2 a + n- ² • (1 -n )(1 + ² а ) B I( B - 1) ] ;

C ₌(1 + 2 а ) [ (1 -n ) В - ( ст q 1 -n5 q ₂ )( B - 1) ]

• 2 =          2n (1 + a - B)(B -1)’

• ^гд^е ° q 1 =^ст q 1 ^{I ст} s 1 ; ^ст q 2 =^ст q 2 ^{I ст} s 2 ; ^C q 1 ^{и ст} q 2 ^{- на}Пр^яжениЯ ^пр^отиво-натяжения оболочки и сердечника соответственно.

Триметаллические заготовки

Для триметаллических заготовок продольные напряжения определяются из решения системы дифференциальных уравнений: для наружной оболочки

R • dG1 / dx + a 11 -G1 + a21 -g2 + a31 = 0,(9-1)

где R = RIR 0 = 1 - A • x ; A = 1 - R 1 IR 0 ; x = x IL    (0 <  x <  1);

a 11 = - C 1 • A ; a 21 = -p 1 • B 1 • A ; a 31 =- C 2 • A ;

для промежуточной оболочки

R • dg2 I dx + a12 • g2 + a22 • G1 + a32 • g3 + a42 = 0,(9-2)

где a ₁₂ = - A ; a ₂₂ = - A • C 3 1 p 1 ; a 32 = - A • B ₂ -p ₂ I p 1 ; a 42 = - A • C 4 I p 1 ;

для сердечника

R • dG31 dx + a13 -G3 + a23 • G1 + a33 • G3 + a43 = 0,(9-3)

где    a₁₃ =- A ;    a ₂₃ = 2 a • AI p ₂ ;    a ₃₃ = A -p 1 I p ₂;    a ₄₃ =- A • C 5 1 p ₂;

C 1 = 2 - A 1 ;   C 2 = A 1 -П 1 • B 1 ;

^C 4 = П 1 ^-Л 2 B 2 ^{- C} 3 ;   ^C 5 = ^{2 a +} П 1 ⁺Л 2 ;

П 1 =^G s 2 ^{I G} s 1 ; П 2 =^G s 3 ^{I G} s 1 ;

a = f ^Itg « _e ;

A 1 = 1 + (1 + 2 a )(1 - R , ²) .

1 - R 1 ²

;

1 + 2 a (1 - R 3 ²). ^C                      ;

³         1 - R 3 ²

B1 =

^R 1 ²    _;

1 - R 1²’

R ²

B 2 = —=?;

² 1 - R 3 ²

R 1 = R c 1 I R ;

R 2 = R c 2 I R ; R 3 = R c 2 I R_c 1 ; R c 1 и R c ₂ - наружный и внутренний радиусы промежуточной оболочки; L - длина очага деформации.

Полученная математическая модель расчета продольных напряжений в слоях би- и триметаллической композиционной заготовки включает основные параметры: gS 1, ав, fn , X, R1, R2, р1, р2, gq и позволяет оценить влияние каждого из них на процесс волочения композиционной заготовки, имеющей конкретную конструкцию.