Напряженно-деформированное состояние слоистых композиционных лопаток с различными физико-механическими свойствами слоев

Очертание лопаток турбомашин в перспективных двигателях становятся более сложными. Вместо современных металлических сплавов начинают применять интерметаллические соединения, композиты с металлической матрицей и композиты с керамической матрицей. По мере совершенствования методов расчета современных реактивных двигателей геометрические характеристики, аэродинамические и температурные нагрузки облопаченных дисков и барабанов становятся более определенными, что дает возможность применять численные методы для определения напряженно-деформированного состояния (н.д.с.) лопаток. В настоящее время благодаря появлению быстродействующих ЭВМ и сложного инженерного программного обеспечения, а также наличию современных композиционных материалов стал возможным более тщательный и точный анализ лопастей перспективных турбовинтовых двигателей. Поэтому, используя полученные в [1, 2] материалы, была составлена программа расчета на ЭВМ, которая позволяет численно определить н.д.с. лопаток из композиционного материала (к.м.).

Составлена программа, предназначенная для исследования н.д.с естественно-закрученных сло-

истых стержневых конструкций, которые находятся под совместным действием растягивающих сил, изгибающих и крутящих моментов или под действием центробежных сил. Каждый слой исследуемого сечения стержня состоит из ортотропного материала с 9-ю независимыми упругими постоянными. При этом целенаправленное регулирование общих свойств конкретного материала может быть осуществлено путем выбора как схемы укладки волокон в отдельном слое, так и расположением слоев с известными свойствами в сечении. Это достигается изменением углов ф i между главными направлениями упругой симметрии материала в слое и осями, в которых исследуется н.д.с. тела. При этом количество независимых упругих постоянных материала слоя в общем случае будет равно 13 [1].

Поперечное сечение рассматриваемых стержневых конструкций является произвольным. Входными параметрами программы являются координаты линии, ограничивающей отдельное произвольное плоское сечение, обычно задаваемое в рабочих чертежах проекта. Это линия разбивается на две части (условно называемое “спинка” и “корытце”), к которым прилегают две наружные в сечении слоя. Координаты наружной поверхности упомянутых слоев задаются. Исходя из этих начальных данных, с помощью специальной процедуры, сечение произвольной конфигурации разбивается на отдельные слои по заданной толщине tc монослоя [3]. Так как размеры сечения могут меняться вдоль длины стержня, то и число слоев в каждом сечении может оказаться различным. Это предопределяет появление коротких слоев внутри сечения. Взятые из разных сечений координаты начала и конца одного слоя определяют длину лепестка в текущем сечении стержня. Следовательно, в программе решается технологическая задача «раскроя» каждого слоя стержня на лепестки в плоскостях, параллельных оси стержня. Координаты и номера построенных точек слоев сохраняются в оперативной памяти ЭВМ [1].

Для исследования н.д.с. слоистого стержня используются основные соотношения разработанной технической теории слоистых стержней [1, 2]. На основе этой теории для каждого сечения вычисляются перемещения, деформации, а также напряжения o_YY, о,„,, о₇₇, c_V7, a_V7, o_Y,, в от- xx yy zz yz xz xy дельных точках слоя i. Входными параметрами для программы являются растягивающее усилие Р, изгибающие М₁, М₂ и крутящий М_t моменты, а также 13 упругих постоянных каждого слоя [1, 2] для текущего слоя. Координаты и номера построенных точек слоев также являются входными параметрами для текущего сечения.

Для исследования н.д.с. стержня в поле центробежных сил, растягивающее усилие, действующее в текущем сечении, вычисляется по формуле [2, 5]

P r = P = to ^{2 R} ( f p dF ) r dr .      (1)

r F ( r i)

Здесь F(r₁) – площадь поперечного сечения; r, R – расстояние от оси вращения до центра тяжести текущего r и периферийного R сечения соответственно (рис. 1); о = k N /360 — угловая скорость (рад.обор./сек.), где N - частота вращения (обор./мин.); r 1 - переменная интегрирования; р -плотность материала слоя сечения. Таким образом, усилие Р в текущем сечении r равно по величине центробежной силе инерции, развиваемой частью слоистого стержня, заключенной между рассматриваемым сечением r и периферийным сечением R.

Для вычисления центробежного усилия по формуле (1) и координат центра тяжести текущего сечения необходимы данные о геометрических характеристиках всех сечений. Для этого сначала вычисляются с помощью специальной процедуры 15 геометрических характеристик и приведенные плотности всех сечений [1].

Вычисляются центробежное усилие для текущего сечения r по приближенной аппроксимационной для (1) формуле [5]

R ^r , + 1

P r = to ² £ f Fp^ dr i = 1 r ,               ,

в которой площадь и плотность текущего сече-

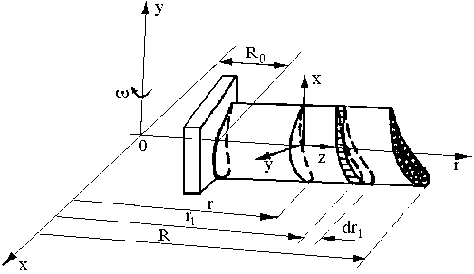
Рис. 1. Система координат в лопатке

ния изменяются линейно относительно предыдущего сечения, т.е.

^F = ^F i ^{+ ( r} 1 - ^r i ^{)( F} i + 1 - ^{F ) /( r} i + 1 - ^r i ),

(3) ^p = ^p i ^{+ ( r} 1 ^{- r} i ^{)( p} i + 1 ^{- p} i ^{)/( r} i + 1 ^{- r} i )•

Далее для текущего сечения исследуется н.д.с. слоистого стержня. Определяются перемещения, деформации, вычисляются физико-геометрические характеристики слоя и всего сечения.

• 1.    ОПИСАНИЕ ИССЛЕДУЕМОЙ ЛОПАТКИ

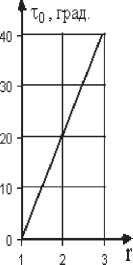
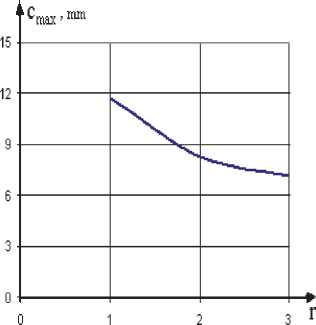
  Рассматриваемая модель лопасти является вариантом натурной лопатки ротора ветроэнергетической установки. Это лопасть была спроектирована и изготовлена с таким расчетом, чтобы соблюдалась конструктивная и аэродинамическая – эквивалентность реальной лопасти. Лопасть, исследуемая в данной работе, представлена тремя сечениями (рис. 2). На рис. 2 приведены изменения наибольшей толщины c_max, относительный угол закрутки т 0 в зависимости от г. Длина хорды постоянная и равна 130 мм., N=1000 об./мин., длина от корневого до периферийного сечения 375 мм.

• 2.    РАСЧЕТНЫЕ ВАРИАНТЫ

3. АНАЛИЗ РЕЗУЛЬТАТОВ РАСЧЕТОВ

В качестве примера по описанной программе была рассчитана лопатка из композиционного материала в поле центробежных сил. При этом было проведено исследование – для трех различных вариантов сочетаний упругих постоянных в пакете слоев композиционной лопатки.

В первом варианте рассматривалась лопатка, состоящая из чередующихся со стороны спинки и корытца слоев стеклопластики.

Во втором варианте рассматривалась лопатка, состоящая из чередующихся со стороны спинки и корытца слоев бороалюминия (ВАL).

В третьем варианте рассматривалась лопатка, состоящая из чередующихся со стороны спинки и корытца слоев керамики (Sic).

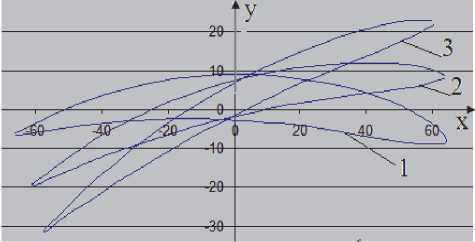
Рис. 2. Изменение угла закрутки на единицу длины лопатки т 0 и с по длине лопатки

ные значения. На входной кромке спинки от кор-

Растягивающее усилие Р при вращении лопатки вычислено по формуле (1) для каждого ее сечения r/R₀. Осредненные значения растягивающих напряжений о cp в условной незакручен-ной лопатке достигают наибольшего значения во втором сечении. Это связано с тем, что усилие Р в третьем сечении отличается от усилия в корневом на 15%, в то время как их площади отличаются на 40%. Для лопаток 2-го типа осредненные напряжения о cp превышают соответствующие величины в лопатках 1, 3 типов. Это связано с тем, что в лопатке 2-го типа имеется более высокий уровень центробежных нагрузок.

По результатам расчетов построены изолинии распределения нормального перемещения W по длине лопатки для спинки и корытца (рис. 3). Как видно из рисунка, нормальные перемещения W на периферийном сечении имеют максималь- невого сечения до третьего сечения перемещения W растет 4-5 раз, а на тонких выходных кромках они растут 10 раз. Распределение нормального перемещения W на спинке более равномерно по сравнению с корытцем лопатки. На корытце концентрация больших перемещении W наблюдается уже во втором сечение лопатки. Поэтому, чтобы увеличить прочность лопатки необходимо слои со стороны корытце заменить материалами, более жесткими на растяжение.

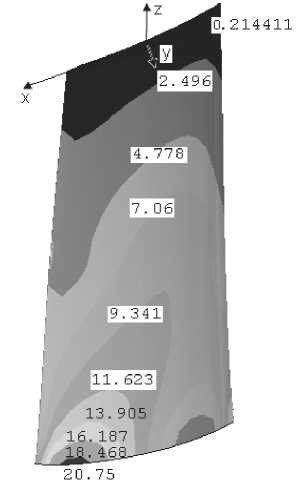
На рис. 4 приведено распределение нормальных напряжений szz а) на спинке б) на корытце по длине лопатки. Наибольшее нормальное напряжение распределена на корневом сечение лопатки (точка М), так как корневое сечение лопатки жестко закреплены. Если это не учитывать, то наибольшие напряжение достигается во втором сечение лопатки и концентрация нормальных напряжении на корытце больше 1.5-2 раза по

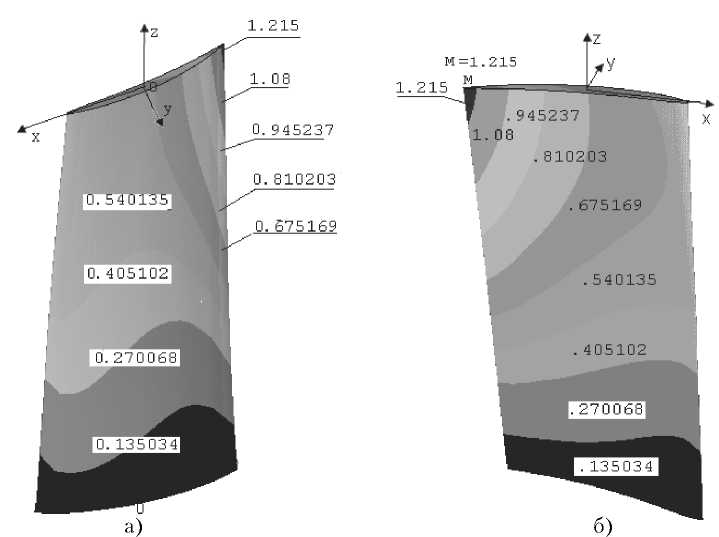
Рис. 3. Распределение нормального перемещения W а) на спинке б) на корытце по длине лопатки.

а)

Рис. 4. Распределение нормального напряжения

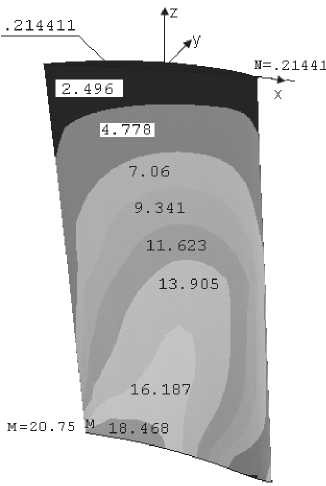
б)

ст zz а) на спинке б) на корытце по длине лопатки

сравнению нормальными напряжениями на спинке. Концентрация нормальных напряжении на третьем сечение меньше 9-10 раз по сравнению c его значениями на корневом сечение.

На рис. 5 приведены распределение касательных напряжений ст yz а) на спинке б) на корытце по длине лопатки. Наибольшее касательные напряжение распределено на втором сечение лопатки. Локальный наибольший растягивающий касательный напряжение ст yz достигается на корневом сечение у входной кромки спинки, а сжимающий – на выходной кромке корытце и его значение (точка N) больше в 2 раза по сравнение с значениями ст yz у входной кромкой спинки (точка М). Как известно в тонких слоях такие кон-

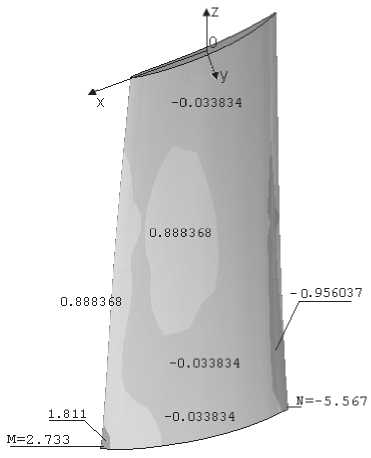
центрации касательных напряжении может привести к местной потере прочности лопатки. Вследствие этого возникновение вышеуказанных величин касательных напряжений в лопатках может оказаться не допустимым. Экспериментально установлено, что запас прочности по касательным напряжениям между слоями в настоящее время не должно быть меньше трех [4].

На рис. 6 приведены распределение касательных напряжений ст xz а) на спинке в) на корытце по длине лопатки. Наибольшее касательные напряжение распределены на втором сечение лопатки. Локальный наибольший растягивающий касательный напряжение ст xz достигается на втором сечение на спинке, а сжимающий – на корытце.

а)                                               б)

Рис. 5. Распределение касательного напряжения ст yz а) на спинке б) на корытце по длине лопатки

а)                                                  б)

Рис. 6. Распределение касательного напряжения и xz а) на спинке в) на корытце по длине лопатки

Касательные напряжение и xz по величине в два раза меньше чем касательные напряжения и yz и распределяется относительно на толстых слоях спинки и корытца. Поэтому по сравнению с касательными напряжениями и yz их влияние на общую прочность лопатки незначительны.

Касательные напряжения и ху своего наибольшего значения достигает во втором сечение (точка N) (рис. 7). По сравнению с значениями касательных напряжении и yz , и xz касательное напряжение и ху незначительно. Поэтому можно его не учитывать при расчетах.

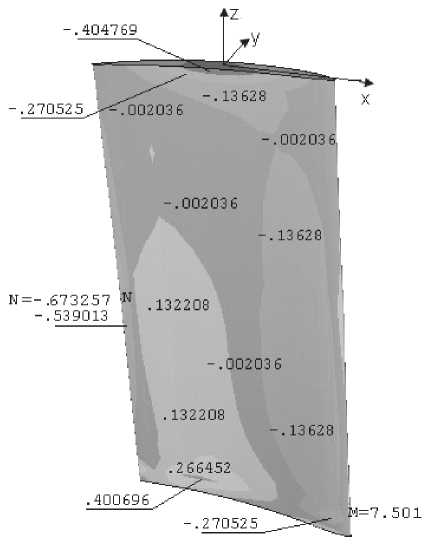
Рис. 7. Распределение касательного напряжения и ху на корытце по длине лопатки

На рис. 8 приведена деформация лопатки относительно оси 0х (пунктирные линии). Наибольшие изменение происходит на третьем сечение лопатки. Значение сжимающей деформации относительно оси 0х на выходной кромке в 3 раза больше чем на входой кромке лопатки. Вследствие этого в тонких слоях выходной кромки может происходить местные потери прочности и поэтому эти слои необходимо заменить материалами со свойствами более прочными на сжатие.

На рис. 9 приведена деформация лопатки относительно оси 0у (пунктирные линии). Наибол-шие изменение происходит на третьем сечение лопатки. Значение растягивающих деформации

Рис. 8. Распределение деформации относительно оси 0х по длине лопатки

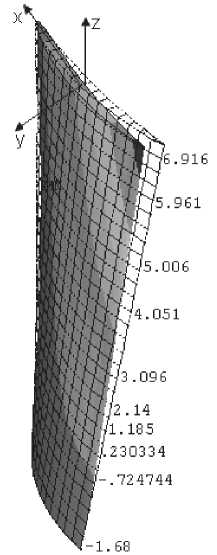
Рис. 9. Распределение деформации относительно оси0у (пунктирные линии) по длине лопатки относительно оси 0у на выходной кромке в 2 раза больше чем на выходой кромке второго сечения лопатки и по своему значению больше в 3 раза чем сжимающая деформация относительно оси 0х. Следовательно в тонких слоях выходной кромки, чтобы избежать потери прочности от сжимающих и растягивющих деформации эти слои необходимо заменить материалами со свойствами более прочными на растяжение и сжатие.

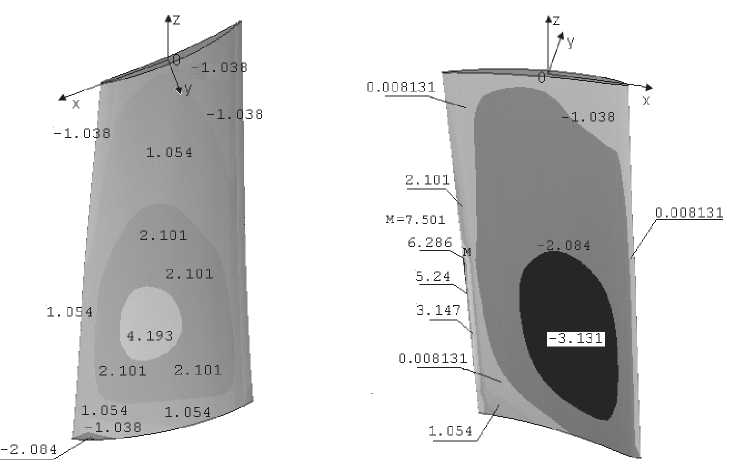
На рис.10 приведена изолинии распределения нормального напряжения и zz в 2, 3 сечениях лопатки. Из рисунка видно, что зона концентрации нормального напряжения и zz на корытце больше по своему значение на 20% от нормальных напряжении и zz на спинке и набольшие нормальные напряжения происходит на втором сечение лопатки. Наибольшие нормальные напряжения и zz происходить в ближлежа-щих к центру тяжести слоях корытца и концентрация нормальных напряжении 2-го сечения больше 2-3 раза от значения нормальных напряжении 3-го сечения лопатки. Вследствие этого необходимо подбирать материалы слоев ближ-лещих к центру тяжести сечения с свойствами более прочными на растяжение.

На рис.11 приведена изолинии распределения касательного напряжения и ху в 2, 3 сечениях лопатки. Из рисунка видно, что зона концентрации касательного напряжения и ху меньше по своему значение на 200%-300% от нормальных напряжении и zz и набольшие касательные напряжения и ху происходит на третьем сечение лопатки. Наибольшие касательные напряжения и ху происходить в ближлежащих к центру тяжести слоях корытца и концентрация касательного напряжении 3-го сечения больше 20-30 раза от значения касательного напряжении 2-го сечения лопатки. В тонких слоях (3 сечение) входной и выходной кромки лопатки сжимающие касательные напряжения распределены равномерно и их значения от наибольщего значения (в ближ-лежащих к центру тяжести слоях) сжимающего

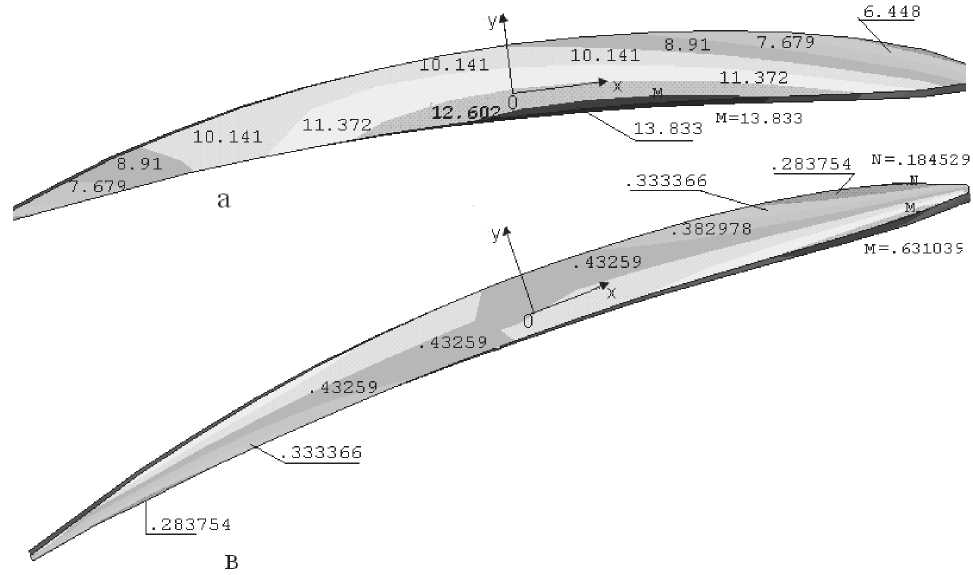
Рис. 10. Распределение нормального напряжения и zz на (а - 2, в - 3) сечениях лопатки

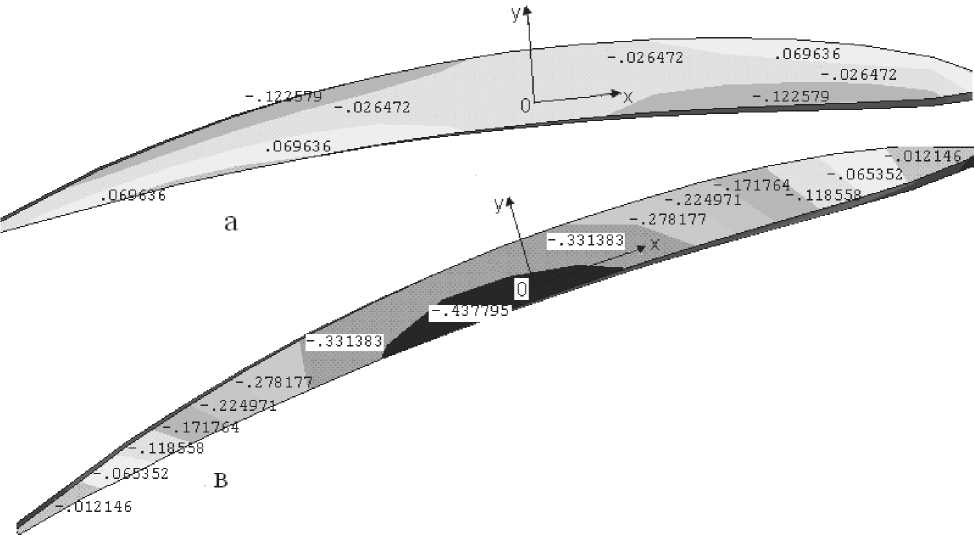
Рис. 11. Распределение касательного напряжении s_ху на (а – 2, в – 3) сечениях лопатки

касательного напряжения больше чем на 4 раза. Поэтому материалы в слоях ближлежащих к центру тяжести должны имет свойства более прочными на растяжение и сжатие.

На рис.12 приведена изолинии распределения касательного напряжения оyz в 2, 3 сечениях лопатки. Из рисунка видно, что зона распределения касательного напряжения оyz меньше по своему значение на 40-50 раз от нормальных напряжении оzz и набольшие касательные напряжения оyz происходит на втором сечение лопатки. Наибольшие растяги-вающие касательные напряжения оyz распределяется в слоях входной кромки лопатки и по своему значению незначительны.

На рис. 13 приведена изолинии распределения касательного напряжения о xz в 2, 3 сечениях лопатки. Из рисунка видно, что зона распределения касательного напряжения о xz меньше по своему значение на 4-5 раз от нормальных напряжении о zz и набольшие касательные напряжения о xz происходит на втором сечение лопатки. Наибольшие растяги-вающие касательные напряжения о xz распределяется в слоях на средней части спинки, а на корытце - сжимающие касательные напряжение. В тонких слоях

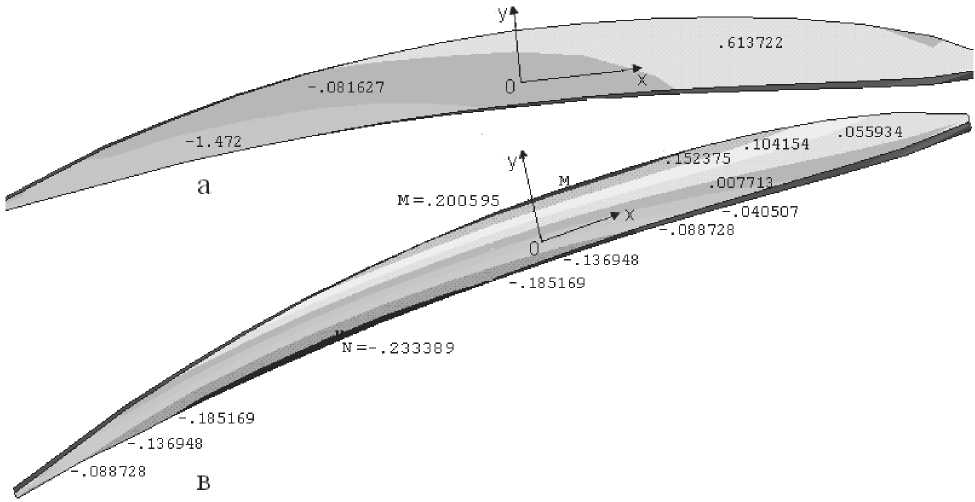
Рис. 12. Распределение касательного напряжения о yz на (а - 2, в - 3) сечениях лопатки

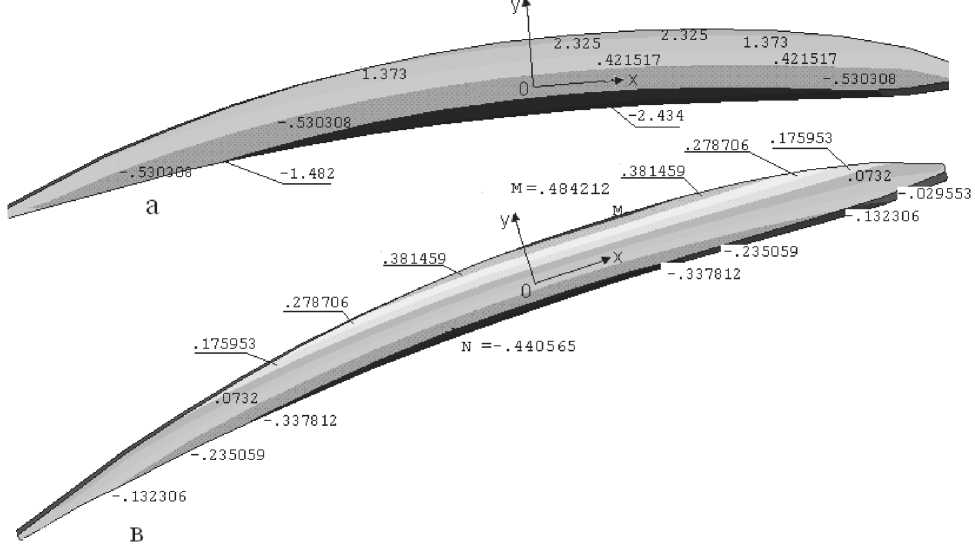
Рис. 13. Распределение касательного напряжения и xz (а - 2, в - 3) сечениях лопатки

(2 сечение) выходной кромки лопатки сжимающие касательные напряжения распределены равномерно и по своему значению незначительны. Наибольшие касательные напряжение и xz по своему значению больше 5-10 раз по сравнению с значениями касательного напряжения и yz и от значения нормального напряжения меньше 4-5 раз. Поэтому для слоистых тонких стержней учет влияние касательного напряжения и xz необходим.

Таким образом, в исследованных примерах показано, что путем выбора материала отдельных слоев или способа армирования в них можно в широких пределах управлять уровнями напряжений и деформаций при одних и тех же физических оборотах ротора.

Таким образом, при заданной геометрической форме лопатки, выбираемой из аэродинамических соображений, посредством перекрестного армирования ее слоев уровень напряжений и zz можно уменьшить, одновременно избежав больших сжимающих напряжений на кромках профиля и достичь более равномерного распределения их ( и zz ) по сечению.

Проведенные расчеты лопаток конкретных типов показали, что при возрастании уровня отношения характеристик жесткости слоев, неравномерность нормальных напряжений в поперечном сечении и величина касательных напряжений между слоями увеличиваются. Наличие больших касательных напряжений между слоями возникает из-за различной жесткости контактирующих слоев. Необходим плавный переход свойств материала от слоя к слою.

Численные исследования естественно-закрученных стержней из к.м. выявили зависи-мость степени неравномерности распределения нормальных напряжений в поперечном сечении от коэффициента упругости c m слоя i, а также взаимосвязанность деформации растяжения и раскрутки при растяжении [1].

Анализ работы многослойных к.м., в условиях близких к рабочим условиям лопаток позволил выявить ряд особенностей распределения напряжений в армированных материалах. Установлено, что при растяжении лопаток из к.м, в поле центробежных сил во внешних слоях происходит увеличение нормальных напряжений в 2-4 раз по сравнению со средними их величинами.