Напряженно-деформированное состояние торообразного баромембранного аппарата комбинированного типа

УДК 531                                                  

Введение . За последние 25 лет развитие мембранной технологии значительно ускорилось. Усовершенствованию установок и аппаратов мембранного вида посвящено немало работ. Так в работе [1] была спроектирована, построена и испытана оригинальная лабораторная установка планарной геометрии мембранной дистилляции для будущего соединения с солнечной энергией. Несмотря на концептуальную простоту, оригинальная геометрия была разработана для того, чтобы обеспечить многоступенчатую компоновку, компактность, внутреннюю рекуперацию тепла и возможную интеграцию с полимерным теплообменником для окончательного нагрева рассола с помощью солнечной энергии или отработанного тепла. Кроме того, было исследовано влияние свободного воздушного зазора, проницаемого зазора и частичного вакуумного расположения воздушных зазоров.

Авторы в [2] предлагают метод многокритериальной оптимизации для определения режимных и геометрических параметров газоструйных аппаратов, приводят результаты расчетов двухступенчатой установки.

В статье [3] на основе концепции создания в аппарате направленного движения материальных потоков рассмотрена возможность интенсификации процессов смешивания сыпучих материалов за счет оптимизации конструкции аппарата. Приведены результаты экспериментальных исследований на модели центробежного смесителя с ротором в виде полого усеченного конуса с волнообразной верхней кромкой. Показано, что модернизация ротора обеспечивает повышение эффективности процесса смешивания в пересекающихся потоках сыпучего материала, позволяя повысить сглаживающую способность аппарата и интенсивность смешивания без дополнительных затрат энергии.

В статье [4] рассматриваются последние разработки по усовершенствованию конструкции мембранного модуля с помощью технологии 3D-печати. В настоящее время существуют стандарты проектирования и расчета прочности аппаратов высокого давления. Работа [5] содержит общую характеристику разработанных стандартов, рассматривает их структуру, подходы, методы расчета и проектирования, а также основные отличия от предыдущих нормативных документов. Авторы в [6] рассматривают вопросы, связанные с расчетом времени выделения пермеата из разделяемой системы при работе баромембранной установки с наиболее распространенным замкнутым контуром циркуляции. Инженерная методика расчета оптимальных конструктивных параметров фланца электробаромембранного аппарата плоскокамерного типа описана в статье [7]. В работах [8–10] авторы разработали конструкцию электробаромембранного аппарата трубчатого типа для очистки технологических растворов, предложили модифицированные уравнения для теоретического расчета и прогнозирования производительности и качества процесса электронанофильтрации. Анализу напряженно-деформированного состояния, учитывающего преобразование формы конструкции путем складывания повторяющихся фрагментов в плоскости наименьшей жесткости, посвящена статья [11]. Также для анализа и моделирования напряженно-деформированного состояния различных элементов аппаратов часто прибегают к методу конечных элементов. Так в работе [14] смоделирован процесс взаимодействия абразивной частицы и поверхности детали, проанализировано ее напряженно-деформированное состояние. Представлены результаты численных экспериментов, которые позволили установить, как распределяются эквивалентные пластические деформации при глубинах внедрения конуса 0,01 мм и 0,05 мм. Таким образом, авторы занимаются вопросами исследования технологических особенностей таких устройств, подбором расчетных схем, методов расчета на прочность и жесткость. В данной работе авторами предложено оптимизировать конструкцию с целью снижения материальных затрат.

Выполненный обзор источников [1–11] по методам расчета конструктивно-технологических параметров и проектирования мембранного оборудования, позволил сформулировать цель работы — разработать перспективную конструкцию аппарата комбинированного типа, определить механические нагрузки на его части, выработать рекомендации по проектированию. Элементы конструкции аппарата (в первую очередь, несущие крышки) должны удовлетворять не только требованиям эффективности и качества разделения и очистки растворов, но и условиям безопасной эксплуатации [12–13]. Поэтому проектирование крышек аппаратов должно производиться исходя из оптимальных конструктивных размеров (толщин круглых пластин, тороидальных оболочек и опорных колец).

Материалы и методы. Базовыми элементами корпуса данного аппарата являются верхняя и нижняя крышки. Они соединены между собой замковым байонетным кольцом (рис. 1). Исходя из того, что крышки имеют одинаковые геометрические размеры, а их нагружение различается только на величину собственного веса, рассматривать будем лишь одну — верхнюю.

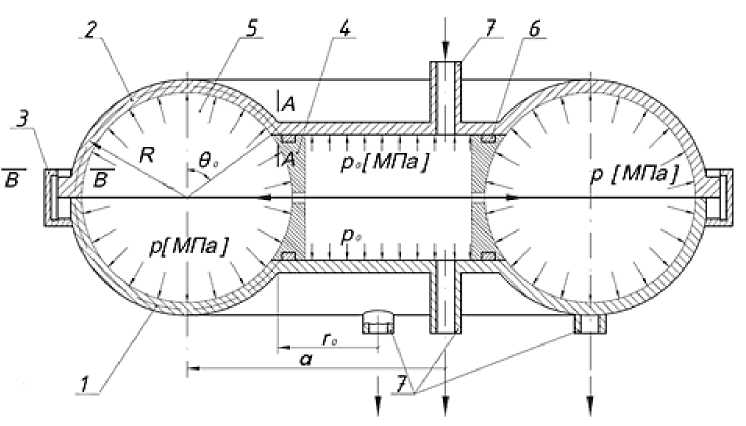
Рис. 1. Конструкция баромембранного аппарата: 1 — крышка нижняя; 2 — крышка верхняя; 3 — кольцо замковое байонетное; 4 — плоскокамерный модуль; 5 — трубчатый модуль; 6 — уплотнение;

7 — входной и выходной патрубки

Рассмотрим расчетную схему данной конструкции (рис. 2). Верхняя крышка находится под воздействием давления на круглую пластину со стороны плоскокамерного модуля и на стенку торообразной оболочки со стороны трубчатого модуля. Показываем неизвестные внутренние усилия в сечениях: А–А (сопряжение оболочки и круглой пластины), В–В (оболочки и кольца), продольную силу T_MB , поперечные силы Q_A , Q_B , изгибающие моменты M_A .

Механика

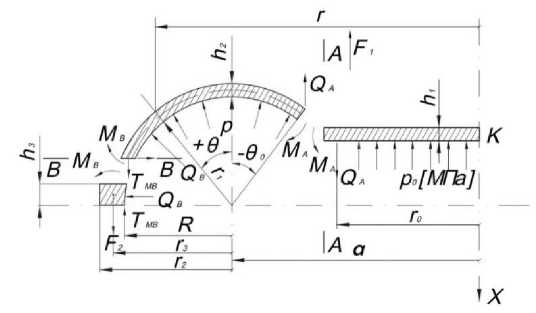
Рис. 2. Расчетная схема крышки

Данные усилия распределены по окружности и, за исключением TMB , являются неизвестными. Они могут быть найдены из условия совместности деформаций.

Введем обозначения: N * , N * , Q * , M A — усилия, обусловленные действием давления p и осевой силы F ;

R — радиус меридионального сечения тора; a — радиус круговой оси тора; r0 — радиус круглой пластины; F = p0пr02 — осевая сила (9 = 91); 90 — угол в месте сопряжения торообразной оболочки и круглой пластины; 0 — переменный угол сечения оболочки; фK — угол поворота кольца; E, v — модуль упругости материала оболочки и коэффициент Пуассона; 9ПЛ — угол поворота пластины; h2 — толщина оболочки; h3 — толщина кольца;  p0

давление на пластину; £ K

радиальное перемещение кольца;

D , =

Eh , 12(1 -v ²)

цилиндрическая жесткость пластины; N = ph₃(а + R ) + Q B ( а + R )  — кольцевое тангенциальное усилие;

h

M = P(а + Г 3 )² - T_M B (а + R )² + M B ( а + R ) + Q B ( а + R ) -^

F ₂ = p ₀ п r ₀ ² + p п [( а + R )² - r ₀²]   — осевое усилие,

Х = ^12(1 -v2) • (аР)13;   0 = R ; TMB =    F2    ; I, h 2          2п( а + R)

кольцевой     изгибающий     момент;

приходящееся на кольцо при 9 = 9 ₀; а =   ;

a

3 а + r               а + r h ln 2 ;  L = — In 2   — геометрические

( а + R J    3  12  ( а + R J

характеристики кольцевого сечения.

Сечение А–А (сопряжение оболочки и круглой пластины)

u A ^{+ а}п ^{( Q}A ^- Q A ) ^{+ а} ₁₂ ⁽ M A ^- M A ) = ^uA™ | 9 ; + « 12 ( Q A - Q A ) + « 22 ( M A - M A ) = -9 ПЛ J

Сечение В-В (оболочка и кольцо)

u _e + а,, ( Q - Q _е) + «, ₂ ( М_е - M _е) = ^ K ; 1 B 11 B-D      B       12 B       B       B

N * = pR

⁹     2

* u

o ci + oisin ⁰ ) ( N   v N • );

Eh ₂        ^{ф 9}

9* =-712(1-v2)

-5Аф(9)Ке[-ХЮ(6)];

l^Eh;

2 + « sin 9 sin 90 2 + а sin 90 -----

1 + а sin 9 sin 9   1 + а sin 9

F1 ф(9) cos 9 ---

2па 1 + а sin 9

XImE [-Xm(9)] +

+ -F'- •

2 па sin 9 ( 1 + а sin 9 )

ш(9)

N * = pR 1 + _Ф 2

sin О _о 2 + а • sin О _о - --

а

sin² О

---

1 F

—---— х

2 п r sin² О 2 п r 1

х<—Л ² ф ( О ) to' ( О ) I_mE ‘[—Лш ( е ) ] + Лф‘ ( О ) I m E ^( оЬ^— *¹;⁰) -

[             to ( 0 ) to ( О ) J

F л sin² О

Q „ = N „ cos О —     1

2 n a ( 1 + а sin О )

1 I

Лto ( О ) J ,

Л L

FhR - ^⁽9)^to'(9)-Re ^ [-^(э)]].

м ; =v м ; .

Оболочку можно считать длинной, если выполняется неравенство

|to^ ) ^— Ю ( ^О,)| >      .

л

Для такого вида торообразной оболочки коэффициенты определяются по формулам:

при

В

M и Q в уравнениях (1)–(2)

a                       2,      [ Re h o ' ] ² + [ I m h o '] ²

• а. =    Лto_n '(1 + а- sin О. ) +

• ¹¹ а 0'            -'     Re h o I m h o ' — I m h o • Re h o '

а = — -1212 — v у2) ■ 1 + а а - s in 6-) ■

^а 22

•

1 Eh ₂ ^;

Re/^- RRe h+ 4I_mhI I-hX' Re Imho, ^10 - h „ hv Re h e ^

[Re h   + [ / „ h _w]²

= 12(1 —v ² ) — •

Лto o ' Re h_w • I_mh_n ' — IX • Re h,„ ' Eh

таблицах

(1–5) ¹

m

•-------------

.

приведены

_{h 2} 2 ^;

значения

функций

ф ( О ), to ( O ), to '( О ), Re h 1 ,Re h 1 ',Re[ —Лto ( О )], I m E [ —Лto ( О )], I m h₁, I m h/ . Данные зависимости будут справедливы для случая, когда Л 3 >  5 . Их можно получить, используя метод асимптотического интегрирования [14].

Угловые и линейные перемещения кольца и круглой пластины могут быть выражены

9 ПЛ

—

p ₀ r ₀³        M_Ar ₀

8 £ >1(1 +v )    £ >1(1 + v )’

u ^ППЛ = 0 — пластина в своей плоскости нерастяжима;

, K = А + ^;

B EI12

KM ф =

BEI

Определяя неизвестные усилия в точках сопряжения оболочки, пластины и кольца M_A , Q_A , M_B , Q_B , можно определить напряжения и деформации в любом сечении крышки: для круглой пластины

а r max

6 M

о*   =    -;

ф max         2   *

h ₁

6 Mr

=  , 2  = v - Оф max > h1

для торообразной оболочки о = о( u)  + о( p)

О max       О max       О max

6 М„  1 + 0,5 а- sin О

= —Л + —----

h 2 ²

•

1 + а • sin О

pr ₁ h 2 ^;

а = а ⁽ u )

ф max       ф max

+ о ( p )

ф max

= 6Мф + ел h22      h2,

Механика

где σ(pm)ax, σ(pm)ax — растягивающие напряжения, найденные по безмоментной теории; σ(um)ax, σ(um)ax — напряжения от изгиба.

Максимальные нормальные напряжения в кольце

K N M ⋅ h 3 2

.

^max  ( a + R )( a + R ) I ₃

Для наибольших напряжений и перемещений в торообразной оболочке используем формулы [15]: для случая θ= 0,

σ_φ ^p =σ _v ⋅ 2,15(1 -ν ²)¹³ ⋅α ^{- 13} ⋅β ²³ + pR , h ₂

в точке θ=±

1, 225

λ

σ θ =±σ v ⋅ 2,99(1 -ν ²) ^{- 16} ⋅α ^{- 13} ⋅β ²³ [ φ ( θ ∗ ) ω '( θ ∗ ) ] + ^{1 + 0,5 α⋅ sin θ ∗} ⋅ ^pR ,

1 +α⋅ sin θ h

F       2    22

где σ _v =     ⁰ ; F ₀ = p π r ₀ ² + p ₀ π ( a ² - r ₀²).

2 π ah ₂

Рассчитать максимальное осевое перемещение в точке А ( θ=θ1 ) и максимальный прогиб в центре пластины можно по формулам:

δ _A = u_XA

2 12(1 -ν ²) ⋅ R ³ ⋅

λ ³     4 Eh ₂ ³ ⋅ a

ПЛ          (5 +ν ) p ₀ r ₀⁴       M_A ⋅ r ₀ ²

u = u ++ .

^{К XA} (1 +ν ) ⋅ 64 D ₁   (1 +ν ) ⋅ 2 D ₁

Условие прочности можно выразить (IV теория)

σ ^IV =  σ ₁ ² +σ ² ₂ +σ ₃ ² -σ ₁ σ ₂ -σ ₁ σ ₃ -σ ₂ σ ₃ ≤ [ σ ] ,

а условие жесткости

U_v <Ги,-К X max X ,

где σ ₁, σ ₂, σ ₃ — главные напряжения в опасных точках крышки; [ σ ] — допускаемое напряжение для материала крышки, [ u_X ] — допускаемый прогиб для крышки в осевом направлении.

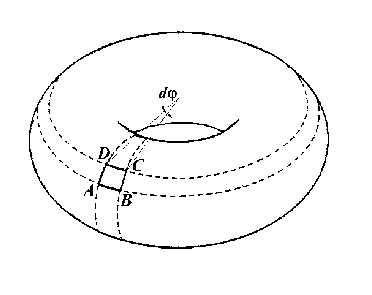
Результаты исследования. На рис. 3 представлена расчетная схема торообразной оболочки.

а )

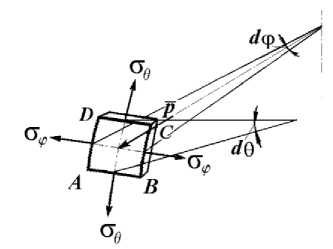
Рис. 3. Расчетная схема торообразной оболочки: а — торообразная оболочка; б — элемент оболочки под действующим давлением

б )

Во время рабочего процесса аппарата действует рабочее давление p0 со стороны плоскокамерного модуля на круглую пластину, со стороны трубчатого модуля на стенки оболочки действует давление p , которое в своем максимальном значении составляет около трети от рабочего.

Кроме зон закрепления оболочки, в которых возникают значительные напряжения, вызванные изгибным эффектом, учитывая тонкость оболочки (  ≤   ) можно принять, что напряжения, возникающие в

оболочке, постоянны по толщине. В этом случае теория называется безмоментной теорией.

Из оболочки, изображенной на рис. 3 а , выделим двумя меридиональными плоскости (т.е. плоскостями, проходящими через ось вращения оболочки) с углом d ф между ними и двумя плоскостями, перпендикулярными оси тора АВ и СD , элемент ABCD .

Нормальные напряжения, действующие по граням АС и ВD , в направлении касательной к окружности, называются окружными напряжениями о_ф. Нормальные напряжения, действующие по граням АВ и CD в меридиональном направлении, называют меридиональными напряжениями о₉. Кроме напряжений о_ф и о₆ на элемент оболочки перпендикулярно поверхности действует внутреннее избыточное давление р .

Уравнение, связывающее между собой эти три величины, является основным в безмоментной теории оболочек и называется уравнением Лапласа:

2t+2* = Р

r R 5

где R — радиус срединной поверхности тора; r — расстояние до оси вращения; 5 — толщина стенки тора.

Для рассматриваемой оболочки и при отсчете угла 0 от вертикальной оси в [13] предлагаются следующие формулы:

для наружной части тора ( 0 < 0 <  90 )

p ( a + R sin 0 ) 2 - a ²

2 5 ( a + R sin 0 ) sin 0

O,

ф

p

( a + R sin 0 ) -

( a + R sin 0 ) 2 - a

2 R sin 0

для внутренней части тора ( 0 ₀ < 0 <  0 )

p a ² - ( a + R sin 0 ) 2 2 5 ( a + R sin 0 ) |sin 0|

O.

ф

5 ⁽ a + R sin e ) +

a ² - ( a + R sin 0 ) 2

2 R sin 0

.

где а — радиус круговой оси тора.

Из условия статического равновесия оболочки, отсеченной цилиндрическим сечением радиуса а , учитывая, что кольцевые волокна при 0 = 0 не деформируются о_ф = 0, а о₆ может быть найдена по формуле:

pR

^0         , для напряжений оф предложена упрощенная формула

„ .0

oA = pR sin.

ф

При проектном расчете с погрешностью до 5 % необходимая толщина торообразной оболочки может быть найдена

— по меридиональным напряжениям

pR

— по окружным напряжениям

pR sin 0

Из полученных величин выбирают большее значение.

При этом для сосудов и аппаратов, работающих под избыточным давлением, стандарт 2 рекомендует следующее условие прочности:

S >  S_p + C ,

Механика

СТП 10–04–02 Расчет на прочность сосудов и аппаратов. Том 1. Расчет на прочность вертикальных и горизонтальных аппаратов / ООО НТП «Трубопровод». Москва, 2005. 190 с.

где C — сумма прибавок к расчетным толщинам стенок, мм; S_p — расчетная толщина стенки (в нашем случае S p =5 ).

Расчет круглой пластины с отверстием, нагруженной внутренним давлением, производится по формулам (32)–(34).

Расчетная толщина пластины:

S i p = K ' K о ' D^] .                                     (32)

Условие выполнения прочности пластины

^> S i p + C .                                                (33)

Обсуждение и заключения . Значение коэффициента K определяется в зависимости от вида соединения частей крышки и для данного варианта соответствует значениям:

s-c

-----< 0,5; K = 0,41 s,-c

S-C

-----> 0,5; K = 0,38

,

Во всех случаях толщина круглой пластины должна быть больше или равна толщине торообразной части.

Значение коэффициента ослабления для пластин, имеющих одно отверстие K ₀ :

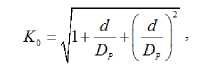
где d — диаметр отверстия.

Если неравенство -1^— >  0,11; S 1 - CD >  0,11 s1-CD>0,11 не выполняется, вводится поправочный коэффициент:

К, =--г==— ^; K = 2,21 + 1 + ( 6 S — CD ) 2.

p 1

1 + J1+

\ V D )

Необходимо учитывать, что прочностные характеристики стеклопластика во многом более высокие, чем у стали. Предел прочности (для металлов — предел текучести) для стали составляет 240 МПа, для алюминия — 50–440 МПа, для стеклопластика — 800–1700 МПа3. Однако, необходимо учитывать, что́ является связующим веществом. Им могут быть полиэфирные, фенол-формальдегидные, эпоксидные, кремнийорганические смолы, полиамиды, алифатические полиамиды, поликарбонаты и др. Выбор связующего вещества оказывает влияние на величину предела прочности стеклопластика.

Допускаемое избыточное внутреннее давление в торообразной части:

И(s - с) =

Допускаемое давление на круглую пластину определяется по формуле

[ р ] =

Г s 1 - с )^: ( K ■ K ₀ ■ D J

•и.

В дальнейшем рассчитанная величина допускаемого избыточного давления умножается на этот коэффициент.

Используя данные таблиц «Физико-механические характеристики композиционного материала» и «Сравнение физико-механических показателей различных материалов», произведем расчет.

В таблице 1 приведены результаты расчета крышек из различных материалов при различном давлении.

В числителе приведены толщины тороидальной части, в знаменателе — круглой пластины.

3Сравнительная характеристика свойств стеклопластика, стали и алюминиевых сплавов / Аквапром : [сайт]. URL: (дата обращения: 22.03.2021).

Таблица 1

Давление, МПа	Материалы
	ПА 6‒210/310 ОСТ 6‒06-С9‒93	ПА66-ЛТО-СВ30	Ст. 3	Композит 4
0,5	0,62/3,46	0,31/2,45	0,25/2,19	0,22/2,14
1	1,24/4,89	0,62/3,45	0,50/3,09	0,45/2,92
2	2,48/6,92	1,24/4,87	0,99/4,36	0,89/4,04
3	3,69/8,47	1,85/5,96	1,49/5,35	1,34/5,02
5	6,18/10,93	3,09/7,71	2,47/6,91	2,23/6,53
10	12,32/15,46	6,16/10,91	4,93/9,77	4,48/9,23

Расчет толщин крышек

Во всех случаях к этим величинам добавляется величина c — сумма прибавок к расчетным толщинам стенок (величина СТП 10–04–02 не нормируется).

Приведенная методика аналитического описания механического воздействия на элементы комбинированного аппарата и выполненный пример расчета торообразной оболочки и пластины позволяют оценить напряженно-деформированное состояние конструкции на прочность и жесткость. Трансмембранное давление, оказываемое на комбинированный аппарат, дало возможность авторам определить необходимые размеры оболочек и пластин для его проектирования и разработки