Напряженно-деформированное состояние трибофатической системы вал-вставка при комбинированном нагружении

Современное машиностроение не перестает активно развиваться, что неизменно ведет к росту эксплуатационных нагрузок, а значит повышает и требования к долговечности и надежности оборудования. Ключевыми факторами в этом случае становятся сопротивление усталости и износу. В условиях высоких нагрузок вопросы оптимизации конструкций и материалов выходят на передний план.

В связи с этим, трибология находится в фазе активного развития, что выражается не только в постоянном расширении областей исследований, таких как износ, инженерия поверхностей, контактная усталость, но и в совершенствовании методов их анализа. Только за 2020-2021 гг. [1] значительное число работ посвящено изучению механизмов износа, моделированию трибологических систем, включая компьютерное моделирование, и созданию новых материалов с повышенной износостойкостью.

Пара «колесо/рельc» является одним из наиболее интересных для трибологии объектов исследования. Есть множество исследований демонстрирующих, что сложность взаимодействия факторов нагружения и геометрии контактирующих тел, может значительно влиять на износ системы характер ее повреждений. Анализ формы контактной поверхности как фактора, определяющего долговечность соединений, проведен в [2], что дополнительно указывает на многообразие сценариев деградации в трибологических парах. В работах [3,4] внимание уделяется локальным видам повреждений, включая фреттинговый износ и контактную усталость, возникающим при различных сценариях нагружения. Режимы повреждений также зависят от геометрии контакта [5–7] и свойств материалов [8,9].

Разработка новых материалов, металлических сплавов, а также различные методы обработки поверхностей для систем, подверженных высоким нагрузкам, — еще одно перспективное направление в решении современных проблем трибологии, что подтверждается большим количеством исследований по рельсовым сталям и высокопрочным чугунам (ADI/CADI) [10–16]. Показано, что варьирование химического состава, режимов термообработки и локальных методов упрочнения позволяет существенно менять механизмы износа и сопротивление контактной усталости. Новые сплавы и чугуны исследуются не только в рамках традиционных экспериментальных испытаний, но и в численных постановках, где конечно-элементное моделирование позволяет воспроизводить контактные процессы и учитывать сложные сценарии нагружения [17–19].

В современной науке, численное моделирование имеет широкое распространение, как инструмент для прогнозирования износа и долговечности элементов, поскольку оно даёт возможность комплексно оценивать напряжённо-деформированное состояние и выявлять зоны зарождения повреждений в условиях трения и переменных нагрузок. В ряде работ показаны примеры численного моделирования контактного взаимодействия элементов и оценкой долговечности. Так, в [20–22] использованы конечно-элементные модели для изучения распределения контактных напряжений и оценки износа зубчатых передач, подшипников и других узлов, что демонстрирует применимость метода для анализа контактных систем. В частности, в [23] предложена модель, позволяющая связать распределение подповерхностных напряжений в скользящих контактах с реальным сроком службы деталей; показано, что именно глубинные максимумы напряжений определяют полезную долговечность и закономерности износа. А в работе [24] трение скольжения для высокоэнтропийного сплава CoCrFeNiMo 0.2 изучалось в широком диапазоне нагрузок и скоростей: численные расчёты позволили оценить чувствительность материала к изменению режимов нагружения и спрогнозировать переход от мягкого к жёсткому механизму износа.

Отдельное направление связано с переходом от традиционного анализа трибологических и усталостных процессов к комплексным подходам. В работе [25] отмечается необходимость интеграции трибологии и механики усталости в единую концепцию трибофатических исследований, что особенно важно для систем, работающих в условиях трения при циклических нагрузках. Также в исследовании вводится понятие опасного объема : в задачах трибофатики опасным объемом называется область деформации, где одновременно действуют контактные и вне-контактные нагрузки.

• 10    mm

176 mm

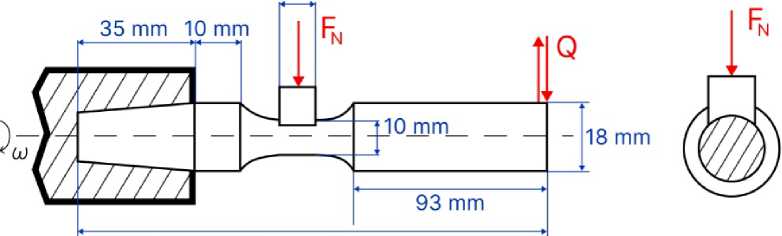
Fig. 1 – Basic scheme of a Tribo-Fatigue shaft-insert system for mechano-sliding fatigue testing

Данное исследование посвящено системе «вкладыш/вал» (Fig. 1), которая является примером простейшей трибофатической системы, предназначенной для испытаний на фрикционно-механическую усталость. То есть механической системы, воспринимающей и транзитно передающей рабочую циклическую нагрузку и в которой одновременно реализуется процесс трения в любом его проявлении [26,27].

Исследуется система, где вал выполнен из конструкционной стали, а вкладыш выполнен из нового материала — чугуна МОНИКА, названного по имени его легирующих добавок (Mo, Ni, Cu). В работах [28–30] глубоко исследуются свойства материала — детально проанализированы механические свойства, включая предел прочности, относительное удлинение, вязкость разрушения и усталостной стойкости в сопоставлении с традиционными сталями и высокопрочными чугунными сплавами. Было показано, что данный материал демонстрирует заметно более высокую долговечность по сравнению с традиционными высокопрочными чугунами и отличается меньшей склонностью к хрупким усталостным разрушениям. Экспериментальные исследования выявили закономерности накопления повреждений, подтвердив более пластичный характер износа и меньшую интенсивность усталостного растрескивания. Более того, в отличие от большинства конструкционных материалов, при увеличении прочности он не теряет пластичности. Даже наоборот, при увеличении прочности, пластичность материала МОНИКА только растет.

Цель настоящей работы заключается в численном анализе напряженно-деформированного состояния системы «вал–вкладыш» из материала МОНИКА при различных режимах нагружения (контактное, изгибное и комбинированное), с определением локализации максимальных напряжений и оценкой объемов потенциального повреждения.

Для достижения поставленной цели решаются следующие задачи:

• •    разработка и верификация трехмерной конечно-элементной модели системы «вал-вкладыш»;

• •    выполнение виртуальных испытаний для четырех сценариев нагружения;

• •    анализ распределения напряжений и выявление зон максимальных значений;

• •    определение опасных объемов для каждого расчетного случая.

• 2    Materials and Methods

  2.1    Analytical approach

Для начальной аналитической оценки напряженно деформированного состояния системы «вкладыш-вал» использована классическая теория изгиба балок, основанная на гипотезе плоских сечений. Предполагается, что сечения, перпендикулярные оси балки, при деформации остаются плоскими и не изменяют своей формы. В этом случае нормальные напряжения в любом сечении определяются зависимостью:

My а ( У ) = —,

где М — изгибающий момент, у — расстояние от нейтральной оси, / — осевой момент инерции сечения.

Максимальные нормальные напряжения O max возникают на максимальном расстоянии y max от нейтральной оси (в крайней точке сечения) и определяются по формуле:

a max

M

W ’

w =

I ymax

где W — момент сопротивления сечения. Для круглого сечения:

W =

nD3

32 ,

где D — диаметр вала.

На основе этих зависимостей построены эпюры изгибающих моментов и нормальных напряжений для всех случаев нагружения (Fig. 2) .

Karchevskaia, A..; Borovkov, A.; Novokshenov, A.; Sherbakov, S.; Klimkovich, N..

Stress-strain state of the Tribo-Fatigue shaft-insert system under combined loading;

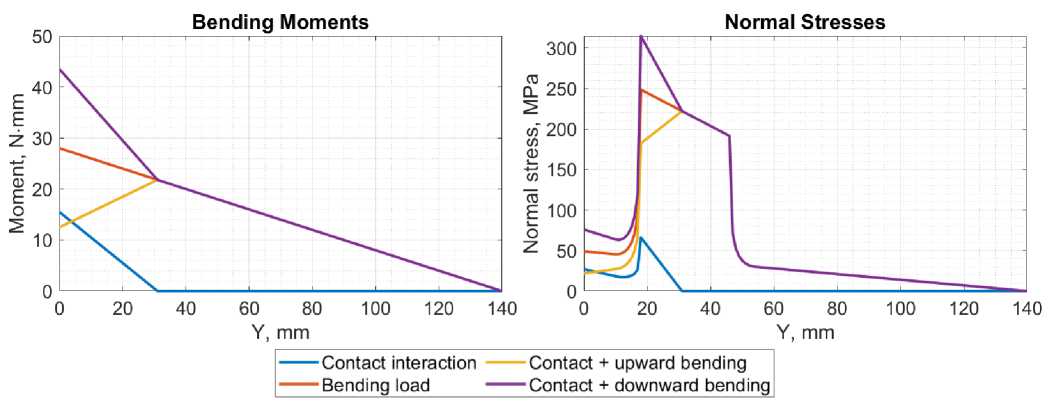
Fig. 2 – Bending moment and normal stress diagrams for all loading cases: (1) contact interaction;

(2) bending load; (3) combined contact and upward bending; (4) combined contact and downward bending

Из полученных графиков видно, что максимальные напряжения для задач контактного взаимодействия, изгибного нагружения, а также их комбинации, где изгибная сила направлена вниз, максимальные напряжения возникают в сечении между областью контактного взаимодействия и зоной закрепления вала и равны 66,2 МПа, 248,7 МПа, 314,9 МПа соответственно. В случае приложения комбинации сил, когда изгибная сила направлена вверх, максимальное напряжение равно 222,2 МПа и возникает в центре контактной площадки.

2.2    Materials

Для аналитических расчетов и при сопоставлении с аналитическими решениями как вал, так и вкладыш принимались выполненными из стали. Однако, в основной части работы по анализу системы «вал–вкладыш» принималось, что вкладыш изготовлен из материала МОНИКА. Характеристики каждого материала приведены в (Table 1) .

Table 1. Material characteristics

Материал v, 1 Е, ГПа а™”’, МПа Cталь 0,3 200 68 МОНИКА 0,28 168 96,7 Где v — коэффициент Пуассона, Е — модуль Юнга, а^1”’ — предельная интенсивность напряжений для определения опасных объемов.

2.3 Finite element modeling of insert-shaft system

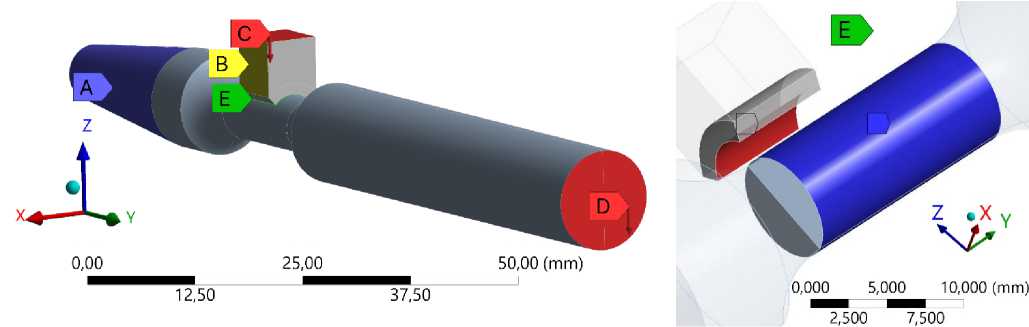
Fig. 3 – Insert-shaft system geometry, geometric conditions and contact surface geometry

Модель включала в себя объемные элементы и учитывала контактное взаимодействие между валом и вкладышем. Обе части системы моделировались в полном объеме без упрощений. Для построения конечно-элементной сетки применялись объемные гексаэдральные элементы первого порядка. Жесткая фиксация (A) наложена на коническую часть вала по всем степеням свободы. Контактная нагрузка (B) в виде нормальной силы |F n | = 500 Н приложена к верхней поверхности вкладыша. Изгибающая сила (C) |Q| = 200 Н действует на свободный конец вала. Для боковых поверхностей вкладыша заданы ограничения нормальных перемещений (D), а также задано контактное взаимодействие между деталями (E). На (Fig. 3) изображены все граничные условия. Коэффициент трения принят равным ^ =0,3. Комбинации граничных условий для каждого расчетного случая показаны в (Table 2) .

Table 2. Combination of boundary conditions for each loading case

Вид нагружения	Граничные условия
Контактное взаимодействие	A + B + D + E
Изгибное нагружение	A + C + D + E
Одновременные нагрузки контактного взаимодействия и изгибного нагружения вниз (вверх)	A + B + C + D + E

• 3    Results and Discussion

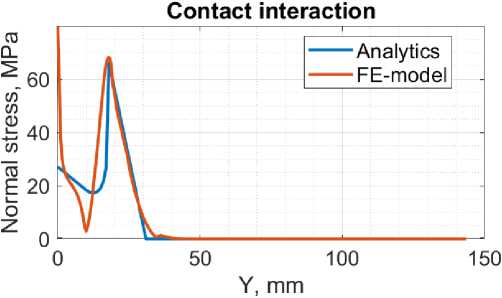
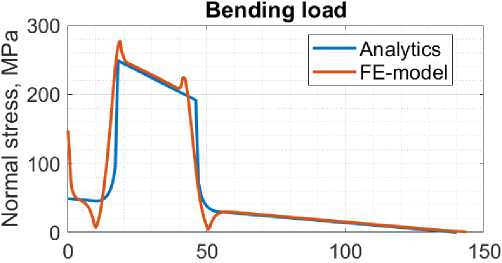
Графики нормальных напряжений конечно-элементной модели (Fig. 4) соответствуют аналитическому решению. Для задач контактного взаимодействия, изгибного нагружения и одновременного условия контактного взаимодействия и изгибного нагружения вниз пики нормальных напряжений в КЭ модели расположены аналогично аналитическому решению и равны 68,3 МПа, 276,7 МПа и 343,2 МПа соответственно.

A)

B)

C)

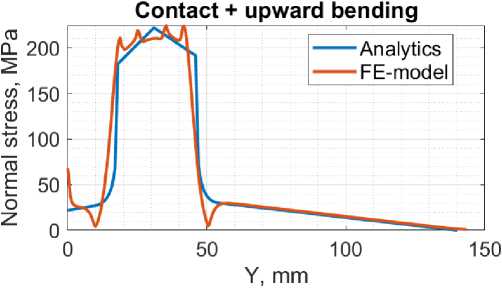
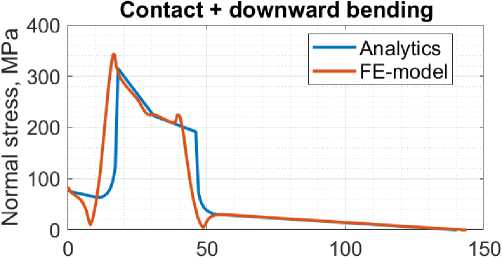
Fig. 4 – Comparison of normal stresses along the shaft axis in the FE model and in the analytical solution for the problem of A) contact interaction; B) bending loading; C, D) Simultaneous contact interaction and bending loading upward, downward

Y, mm

D)

Для задачи одновременного контактного взаимодействия и изгибного нагружения вверх наибольшее значение напряжений смещено относительно аналитического максимума вправо и равно 224,6 МПа. Таким образом, решение конечно-элементной модели отличается от аналитического на 3,2%, 11,3%, 9,0% и 1,1% соответственно для каждой задачи.

После верификации стальной модели далее расчеты проводились с материалом МОНИКА. Для полноты исследования опасных объемов были увеличены нагрузки на систему: в задачах исследовались комбинации контактной нагрузки на вкладыш |F n | = 1000 Н и изгибающей силы |Q| = 200 Н.

Ключевым результатом данной работы стало определение распределения напряжений и их максимумов в системе «вал–вкладыш» при различных сценариях нагружения, при условии, что вкладыш выполнен из материала МОНИКА. Полученные результаты виртуальных испытаний для различных случаев нагружения системы вал/вкладыш, где вкладыш изготовлен из конструкционного материала МОНИКА, представлены на рисунках (Fig. 5 – Fig. 8) .

Fn

Stres

OE+OO

No Result

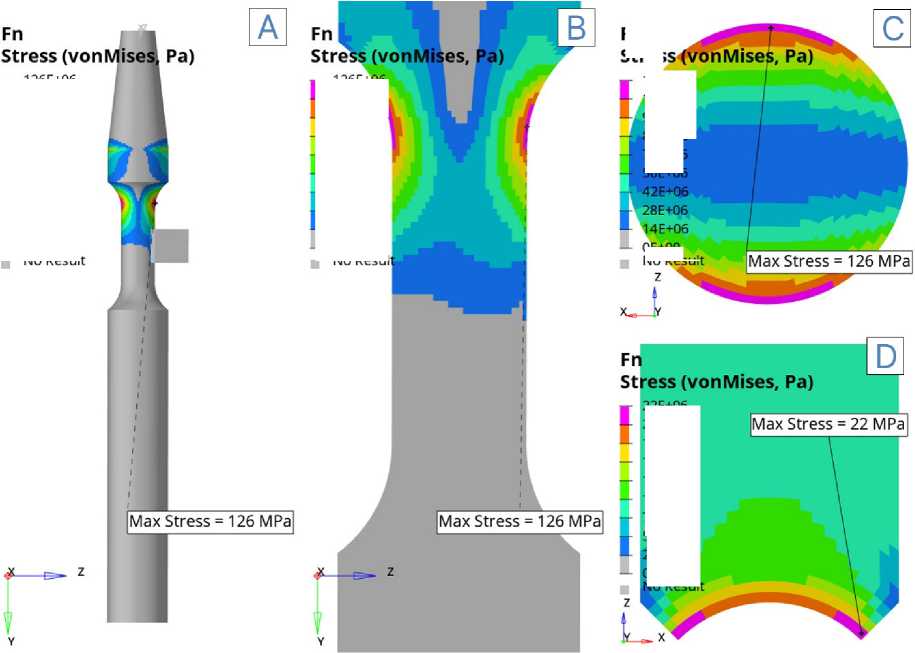
Fig. 5 — Von Mises stress intensity in the insert-shaft system (MONICA) in case of contact interaction: A) in the whole system; B) in the longitudinal section of the shaft; C) in the cross-section of the shaft at the point of maximum stress, D) in the cross-section of the insert at the point of maximum stress

126E+06

112E+06

98E+06

84E+06

70E+06

56E+06

42E+06

28E+06

14E+06

OE+OO No Result

112E+0^ 98E+06 1

84E+06

70E+06

56E+06

42E+06

28E+06

14E+06

OE+OO No Rest

126E+06 112E+06

98E+06

84E+06

70E+06 56E+06

22E+0O

20E+06

17E+06

15E+06

12E+06

10E+06

7E+06

5E+06

2E+06

OE+OO

No Result

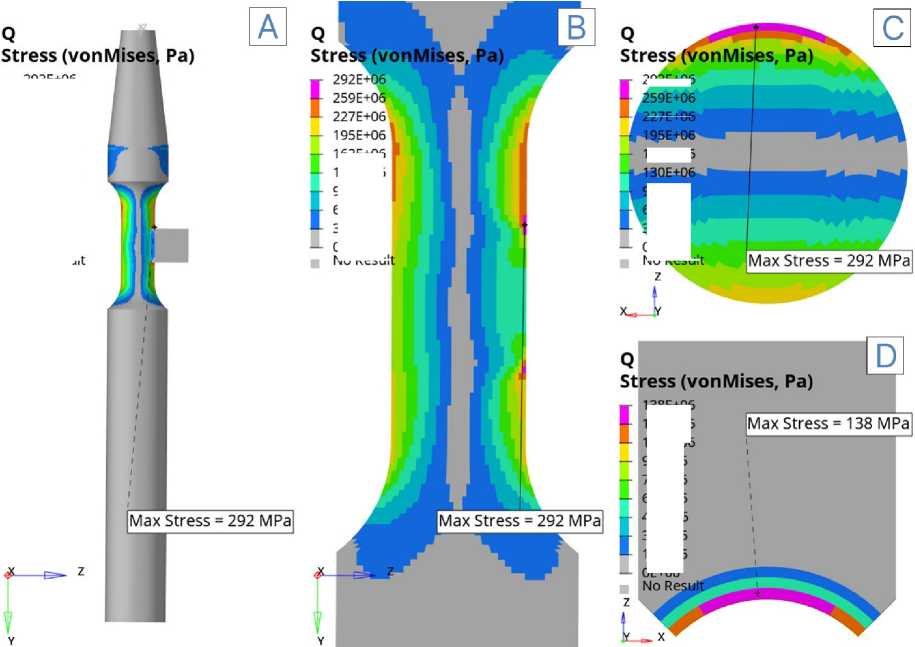
Результаты моделирования показывают, что характер распределения напряжений в системе «вал–вкладыш» существенно зависит от сценария нагружения. При действии только нормальной силы (Fig. 5) максимальные напряжения достигают 126 МПа и локализуются в зоне контакта на поверхности вала. При чистом изгибе (Fig. 6) напряжения достигают 292 МПа, концентрируясь в переходной области сечения вала. Совместное действие контактной и изгибающей нагрузки (Fig. 7 и Fig. 8) приводит к формированию более высоких значений: при изгибе вверх максимальное напряжение составило 376 МПа, а при изгибе вниз — 268 МПа, при этом критические области также приходятся на контактную поверхность вала и зоны сопряжений. Таким образом, наибольший уровень напряжений возникает при действии сонаправленных контактной нагрузки и изгибающей силы, тогда как совместное нагружение в противоположных направдениях нагрузок приводит к перераспределению напряжений и снижению их пиковых значений по сравнению с чистым изгибом.

227E+06

No Result

No Result

Fig. 6 –– Von Mises stress intensity in the insert-shaft system (MONICA) in case of bending loading:

[ 292Е+06

259Е+06

227Е+06

— 195Е+06

— 162Е+06

— 130Е+06

Й 97Е+06

65Е+06

32Е+06

— ОЕ+ОО

No Result

162Е+06

130Е+06

97Е+06

Б5Е+06

32Е+06

ОЕ+ОО

292E+06

162E+06

97Е+06

65Е+О6

32Е+06

ОЕ+ОО

138E+06 123E+06

107E+06

92E+06

77E+06

61E+06

46E+06

31Е+Об

15Е+06

ОЕ+ОО

A) in the whole system; B) in the longitudinal section of the shaft; C) in the cross-section of the shaft at the point of maximum stress, D) in the cross-section of the insert at the point of maximum stress

Fn+Q mul

Stress (vonMises, Pa)

5 137E+O6 121E+06 106E+06 91E+06 76E+O6

- 61E+06

- 46E+06

- 30E+06

- 15E+06 - OE+OO

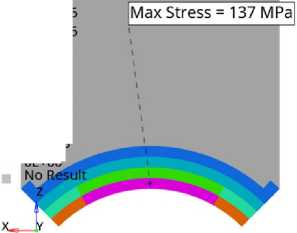
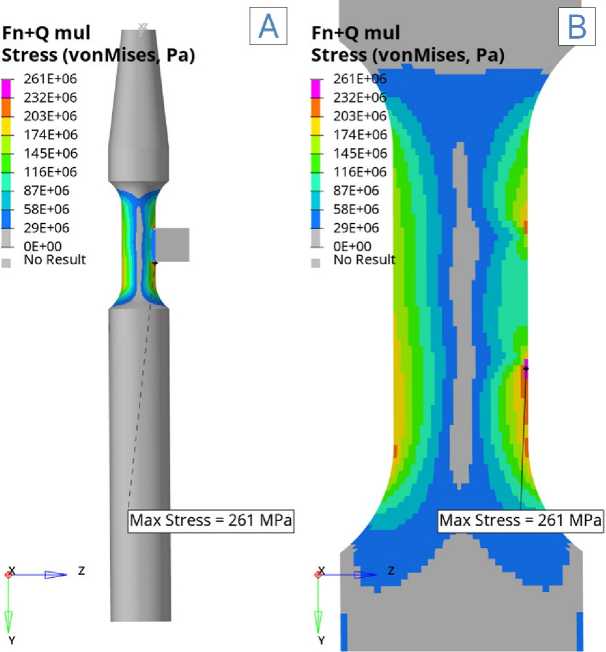
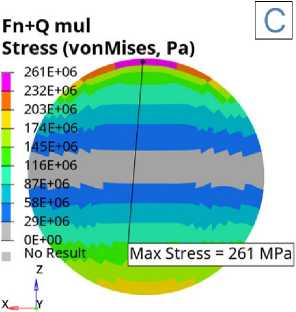
Fig. 7 –– Von Mises stress intensity in the insert/shaft system under simultaneous contact interaction and upward bending load: A) in the whole system; B) in the longitudinal section of the shaft; C) in the transverse section of the shaft at the point of maximum stress; D) in the transverse section of the insert at the point of maximum stress.

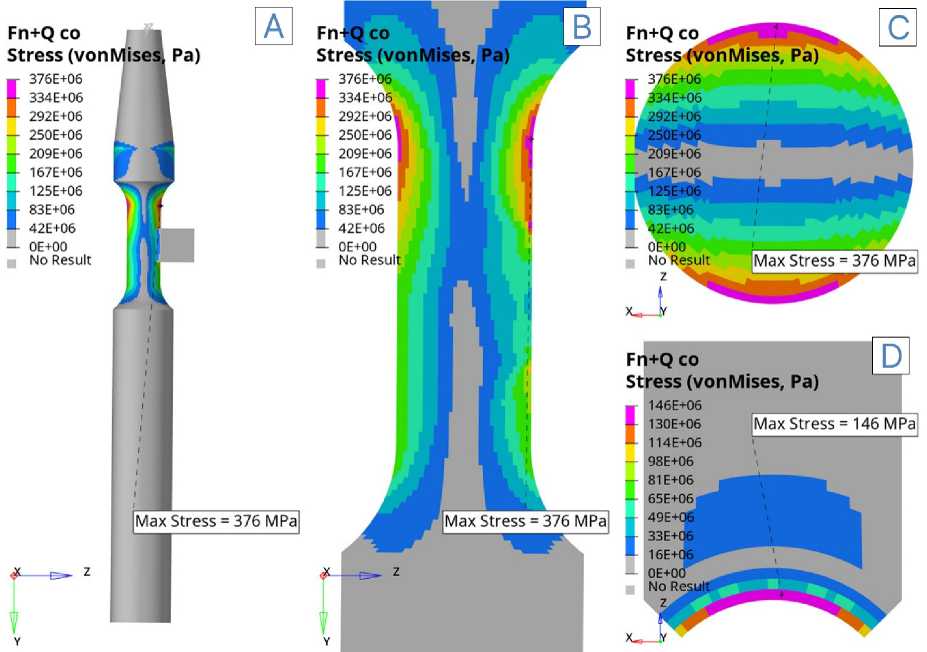
Fig. 8 — Von Mises stress intensity in the insert/shaft system under simultaneous contact interaction and downward bending load: A) in the whole system; B) in the longitudinal section of the shaft; C) in the transverse section of the shaft at the point of maximum stress; D) in the transverse section of the insert at the point of maximum stress.

В опасных объемах происходит накопление параметра повреждаемости материала, что при большом числе циклов нагружения приводит к его разрушению. Для рассматриваемой в рамках данной работы системы предельные интенсивности напряжений, по отсечению которых определяются опасные объемы, равны 96,7 МПа и 83,3 МПа для вкладыша и вала соответственно. На рисунках (Fig. 9) и (Fig. 10) представлены опасные объемы, полученные для каждого расчётного случая, возникающих в вале и вкладыше соответственно.

Для выбранных величин нагрузок (F n = 1000 Н, Q = ± 200 Н) опасные объемы возникают как в вале, так и во вкладыше. При изолированном контактном взаимодействии величина опасного объема составляет 0,2% от общего объема вала или 75 мм³. При наличии только изгибной нагрузки величина опасного объема составляет 3,4% от общего объема вала или 1216 мм³. Для задач с условием одновременного нагружения величина опасных объёмов в вале различается в зависимости от направления изгибной нагрузки. В частности, при изгибе вниз опасный объём составляет 5,6% от общего объёма системы (или 1976 мм³), тогда как при изгибе вверх это значение уменьшается до 2,8% (990 мм³).

Во вкладыше опасные объемы возникают во всех случаях, кроме задачи только контактного нагружения. Возникающие опасные объемы составляют 1,1%, 1,8% и 0,9% (12 мм³, 19 мм³ и 9 мм³) для остальных задач соответственно. Увеличение опасного объёма в случае контактного взаимодействия и изгиба вниз, относительно случая с одним только изгибным нагружением объясняется действием силы F_n, провоцирующей контактное взаимодействие и возникновение дополнительных напряжений, что приводит к большему накоплению повреждений.

Fn

Stress (vonMises, Pa)

A

Q

Stress (vonMises, Pa)

22E+06

20E+06

17E+06

15E+06

12E+06 No dangerous

10E+06

7E+06

5E+06

2E+06

OE+OO No Result

volumes

[ 138E+06

123E+06

107E+06

— 92E+06

— 77E+06

— 61E+06

— 46E+06

I 31E+06

I 15E+06

— OE+OO

No Result z

Fn+Q co

Stress (vonMises, Pa)

I 146E+06

13OE+06

114E+06

— 98E+06

— 81E+06

— 65E+06

— 49E+06

■ 33E+06

I 16E+06

— OE+OO No Result

Fn+Q mul

Stress (vonMises, Pa) [137E+06

121E+06

106E+06

- 91E+06

— 76E+06

- 61E+06

- 46E+06

30E+06

- 15E+06 — OE+OO No Result z

Fig. 9 — Dangerous volumes in insert for case A) contact interaction; B) bending load; C, D) Simultaneous contact interaction and bending load upwards, downwards

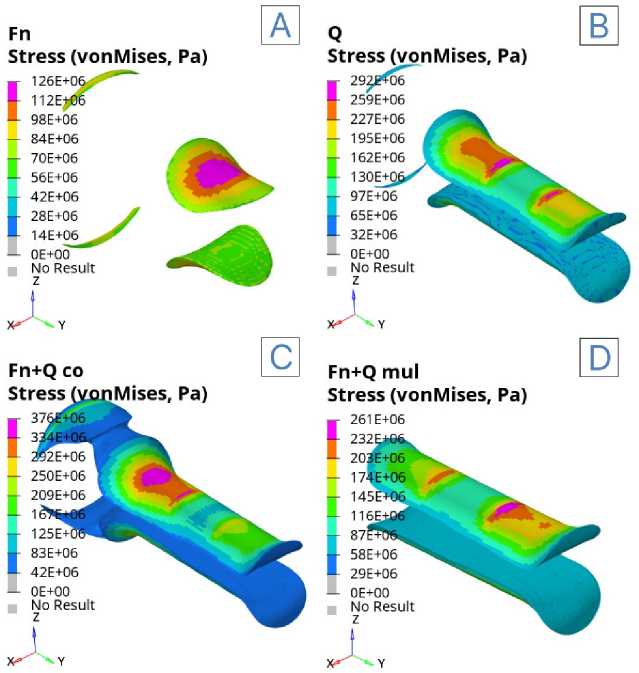
Fig. 10 — Dangerous volumes in the shaft for case A) contact interaction; B) bending load; C, D) Simultaneous contact interaction and bending load upwards, downwards

• 4    Conclusions

Таким образом, в данной работе разработана и верифицирована трёхмерная конечноэлементная модель трибофатической системы «вал–вкладыш», которая описывает напряженно-деформированное состояние при различных вариантах внешнего нагружения: контактное взаимодействие, изгибное нагружение, комбинированные сонаправленные и комбинированные противонаправленные нагрузки. Верификация расчетных данных показала расхождение с аналитическим решением на 3,2%, 11,3%, 9,0% и 1,1% соответственно для каждой задачи, что является подтверждением достаточной точности модели.

В результате проведенного численного анализа системы вал/вкладыш, где вкладыш изготовлен из материала МОНИКА, были получены значения напряжений, возникающих в рассматриваемой системе, а также исследованы величины опасных объемов для каждого расчётного случая. Показано, что направление изгибной составляющей играет решающую роль как в величине, так и в распределении напряжений. Если изгибающая сила действует в том же направлении, что и контактная нагрузка, то максимальные значения сосредоточены на одной стороне контактной поверхности; изменение направления изгиба влияет на максимумы напряжений, что, в свою очередь, влияет на размер и форму потенциально опасных областей. Относительный объем таких зон при определенных сочетаниях усилий может достигать нескольких процентов материала детали, что значительно выше, чем в случаях раздельного нагружения.

Разработанная конечно-элементная модель позволяет установить зависимости для прогнозирования эксплуатационных характеристик системы «вкладыш-вал» с целью дальнейшей интеграции с прогностическими моделями на основе искусственного интеллекта. Такой подход открывает практический потенциал для оптимизации геометрии и несущей способности узлов трения, работающих в сложных условиях нагружения.

• 5    Acknowledgements

  Работа выполнена при поддержке Российского Научного Фонда, проект № 23-РБ-09-27 от 15.12.2023, а также при поддержке Белорусского республиканского фонда фундаментальных исследований (проект № Т24СПбГ-003).