Напряженно-деформированное состояние в окрестности вершины составного клина с жестко защемленными образующими

PNRPU MECHANICS BULLETIN

При исследовании напряженного состояния вблизи особых точек однородных и составных деформируемых тел (вершин клиньев, конусов, трещин, ребер (пересечений образующих поверхностей) и т.п.) обычно рассматривается локальная задача в криволинейной системе координат, полюс которой помещается в особую точку [1-17 и др.]. Асимптотическое решение такой задачи разыскивается в виде разложения по собственным функциям однородных задач с множителями rXk, где r - расстояние до особой точки, а Xk - соответствующее собственное значение. По значениям Xk выносится суждение о характере напряженного состояния вблизи особой точки. В рассматриваемом подходе, во-первых, не принимаются и не могут быть приняты во внимание ограничения, задаваемые непосредственно в особой точке. В полюсе тензорные характеристики (напряжения, деформации, перемещения) не определены, так как здесь отсутствует взаимнооднозначное соответствие между физической точкой тела и ее криволинейными координатами. Во-вторых, особая точка рассматривается как математическая (не имеющая линейных размеров), поскольку допускается, что параметр r может принимать сколь угодно малые значения. Такое представление о точке сплошной среды не соответствует ее по- стулатам, согласно которым точкой является представительный объем материала тела, имеющий конечный характерный размер. Данное несоответствие приводит к тому, что при построении решения асимптотическим методом в окрестности особой точки используется представление о напряжениях и деформациях в элементарных объемах с характерными размерами, меньшими характерных размеров макроскопических представительных объемов изучаемых тел. Фактически это означает переход на микро-уровень с сохранением физических уравнений макроуровня. Данное обстоятельство ограничивает достоверное применение асимптотических методов областью вне малой окрестности особой точки. Внутри такой окрестности возможность использования асимптотического решения требует дополнительного изучения.

Отождествление особой точки с представительным объемом тела дает возможность сформулировать в ней задаваемые ограничения (граничные условия, условия непрерывности параметров состояния на поверхностях соединения, кинематические ограничения и т.п.). При этом оказывается, что необычность особых точек проявляется в том, что количество независимых ограничений в них оказывается большим, чем количество ограничений в обычных точках границы тела, поэтому задачи для тел с особыми точками являются переопределенными. Ограничения на параметры состояния в особых точках представляют собой систему линейных неоднородных алгебраических равенств. Изучение этих равенств позволяет в зависимости от геометрических и материальных параметров элементов конструкции установить возможные варианты постановки задачи механики деформируемого твердого тела, содержащего особую точку, выявить критические сочетания конструктивных параметров и параметров нагрузки. Все это необходимо для построения решения, удовлетворяющего всем ограничениям в особой точке и согласующегося вне малой окрестности с решениями, получающимися классическими методами.

В настоящей работе развиваемый авторами подход [18–20] применяется для исследования напряженно-деформированного состояния (НДС) в вершине и ее окрестности составного клина с жестко защемленными образующими. Асимптотическое решение подобной задачи рассматривалось, например, в работах [7–9].

1.    Постановка задачи о формировании ограничений в вершине клина

Рассматривается часть конструкции, представляющая собой плоский клин, составленный из двух изотропных линейно-упругих элементов 1 , 2 , скрепленных между собой (рис. 1). Образующие клина защемлены. Орты n и m перпендикулярны образующим, а орты n ' , m 'перпендикулярны соответственно направлениям n , m . Углы а , р при вершинах, составляющих клин элементов, подчинены условиям

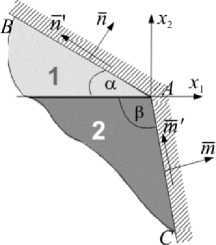
Рис. 1. Составной клин

Fig. 1. Compound wedge

0 <а< 2 п , 0 <в< 2 п , 0 <а + Р< 2 п . (1)

Вводится ортонормированная декартова система координат x ₁, x ₂с началом в точке А (вершине клина). Ось x ₁ направляется по касательной к линии соединения составляющих клин элементов во внешнюю, относительно клина, область. Приняты обозначения

°(k), г(/)— компоненты тензоров соответственно напряжений и деформаций в к-м (к = 1,2) составляющем элементе клина. Ек, Gk, vк, toк - модуль Юнга, модуль сдвига, коэффици- ент Пуассона, коэффициент температурной деформации в к-м элементе клина; г®, г^

–

относительные удлинения линейных элементов в точке А , направленных по образующим AB и AC ; ф 1 и ф ₂- изменения в процессе деформирования соответственно углов а , р ; A T - приращение температуры. Считается, что составной клин находится в условиях плоской деформации. Согласно принятой концепции в окрестности точки А рассматриваются две особые точки. Это представительный объем тела 1 , содержащий точку А , и представительный объем тела 2 , содержащий эту же точку. Указанные представительные объемы находятся в однородном НДС и взаимодействуют по линии соединения. Это взаимодействие характеризуется условиями:

непрерывности напряжений и деформаций на линии соединения

(1)       (2)        (1)       (2)       (1)(2)

° 22 ° 22 , °12 °12 ,   £11

отсутствия относительных удлинений в направлении образующих составного клина е^ = 0, г^ = 0;

отсутствия сдвига между направлениями AB и AC

Ф1 +ф2 = 0.(4)

С введением обозначений

(1)       (2)              (2)              (1)                          2

^г 11     ^г 11      ^£ 11 ; ^г 12 ^г 12 ; ^г 12     g ^O 12 ; g , Q

G ₁

^{(1 + v} 1^{) to} 1 g l ivjto - (1 - 2 V 1 ) (1 - 2 v 2 )

A T

равенства (2)-(4) для случая, когда sin а ^ 0 и sin р * 0 (случай sin а = 0 и sin р = 0 рассматривается в п. 2) приводятся к системе уравнений

8 11 cos² а + £ 22 sin² а - g г ₁₂ sin 2 а = 0,

8 11 cos² Р + г 22) sin² Р + г ₁₂ sin2 p = 0,

^£ 11^(ct g ^{а +} ctg P ) + S ₁₂(1 ^- g ) = 0,                               (6)

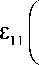
^v 1 _ ^{g v} 2 ) , (1) ¹ — ^V 1 _ (2) g O-^ ) Q I O')*)                    O^a

1 - 2 v 1 1 - 2 v ₂ J    ²² 1 - 2 v 1     ²² 1 - 2 v ₂

При построении равенств (5), (6) использовались физические уравнения линейной термоупругости и формула

Ф sin y = [ ^{2 0} rp - ⁽ n к ⁺ П 1 ) 3 rp ] ^кг¹р , ⁽⁷⁾ определяющая сдвиг ф в произвольной точке сплошной среды между линейными элементами с направлениями к , 1 и углом у между ними. Здесь п _к , п ₁ - относительные удлинения в точке сплошной среды в направлении ортов к , 1 соответственно; 8 rp - координаты единичного тензора.

Задача состоит в исследовании (в зависимости от материальных и геометрических параметров) существования решений системы уравнений (6) и ее аналогов в случаях sin а = 0, sin р = 0; определении в каждом решении независимых ограничений на параметры состояния в особой точке.

2.    Общее исследование системы уравнений (6) 2.1.    sin a ^ 0, sin в ^ 0.

Данное условие обеспечивает существование третьего из равенств системы уравнений (6). Эта система автономна относительно деформаций £ 11 , £^ , £ 22? , £ 12 . Ее определитель вычисляется по формуле

А = 2 g sin(a + в)

1 -vi —    • о , 1-V2 — о •

----— cos a sin в +--— cos в sin a 1 - 2 v 1              1 - 2 v ₂

2(1 - g )

1 g Uin'./on'n 1-V1 sin2 R + g(1 ^UrnA/ sin a sin вsin p+sin a v 1 - 2v1 1 - 2v2 )               1 - 2v1          1 - 2v2

Определитель (8) зависит от пяти безразмерных параметров a, в, g, v1, v2. Если сочетание этих параметров не обращает в нуль определитель (8), уравнения (6) имеют единственное решение р = А     = А2  Д2) — А3  ₽ — А4

^£ 11       . ,     ^£ 22        ■ ,     ^£ 22        . , ^£ 12 . ,

А       А       А А где Аi (i = 1, 2, 3, 4) - определители матриц, получающихся последовательной заменой столбцов матрицы системы уравнений (6) столбцом свободных членов:

А 1 = - 2(1 - g ) Q sin² a sin² в , А ₂ = 2Q cos a sin P (cos a sin в + g cos в sin a ),

А ₃ = - 2 Q sin a cos в (cos a sin в + g cos в sin a ), А 4 = Q sin a sin в sin( a + в ).     (10)

Определители (10) одновременно обращаются в нуль в случаях:

• 1)    Q = 0. Это возможно в случае отсутствия температурной нагрузки (А T = 0) или при условии зависимости между материальными характеристиками скрепляемых тел, обращающих в нуль коэффициент при А T (5):

® 1 (1 + v ₁) - g to ₂(1 + v ₂) = 0

1 - 2 v 1        1 - 2 v ₂

Если определитель (8) в данном случае не равен нулю, все деформации (9) в особых точках обращаются в нуль. С учетом зависимости (5) в особых точках формулируются шесть ограничений на деформации. Если определитель (8) обращается в нуль, уравнения (6) становятся линейно зависимыми. Количество независимых ограничений на компоненты деформации определяется рангом матрицы системы;

• 2)    g = 1, a + в = п . Система (6) приводится к трем линейным неоднородным уравнениям относительно четырех компонентов деформации

£ 11 cos² a + £ 2 ¹₂⁾ sin² a - g £ ₁₂ sin 2 a = 0, £ 11 cos² a + £ 22) sin² a - £ ₁₂ sin 2 a = 0,

^£ 11

^v 1

^v 2

1 - 2 v 1 1 - 2 v ₂

_{+ £} (1) ^{1 v} 1

²² 1 - 2 v 1

(2) C ¹ -^) _

^£22 . _n ^Q .

^{1 - 2 v} 2

Если коэффициенты Пуассона скрепляемых тел различны ( v 1 ^ v ₂), ранг системы

• (12)    равен трем, и компоненты деформации связаны независимыми соотношениями

  ^£ 11

  
  

  Q (1 - 2 v 1 )(1 - 2 v ₂) sin² a

  ^V 1 ^-V 2

  
  

  -£ ₁₂ sin 2 a ,

  
  

  (1)       (2)

  ^£ 22     ^ь 22

  
  

  _-

  
  

  Q (1 - 2v, )(1 - 2v, )cos² a       . .

  —-----1^----- 2- ------+ s ₁₂ sin 2 a .

  ^v 1 ^-v 2

  
  

  Когда коэффициенты Пуассона скрепляемых тел одинаковы ( v 1 = v 2 ), но Q * 0 вследствие различия коэффициентов линейного расширения ( ю 1 * ю ₂ ), ранг системы уравнений (12) равен двум, а ранг ее расширенной матрицы – трем. Уравнения несовместны. Это означает, что при стремлении v 1 к v ₂ деформации в вершине клина неограниченно возрастают;

  3) g = 1, a + в = 2 п . Система (6) принимает вид (12), поэтому справедливы результаты, приведенные в п.2).

  
  

  2.2. sin a = 0, sin в * 0, (a = п).

  Стороны угла a = п представляют собой прямую. При деформировании окрестности точки А прямые переходят в прямые, поэтому сдвиг между образующими развернутого угла равен нулю. Следовательно, условие (4) ( ф 1 + ф ₂ = 0) при a = п переходит в условие ф ₂ = 0. Уравнения (6) принимают вид

  
  

  ^£ 11    0,

  £ 11 cos² в + £ 22) sin² в + ^£ i₂ sin 2 в = 0,

  £_n ctg P + 2 £ 12 = 0,

  
  
  
  

  ^£ 11

  
  

  1 1 - 2 v 1

  
  

  1 - 2 v 2

  
  

  ^{+ £} 22

  
  

  ^{1 -v} 1   Д2) £ (1-^ 2) _

  ^£??

  1 - 2 v 1     ²² 1 - 2 v ₂

  
  

Определитель матрицы системы уравнений (13)

А = 2

^{1 -v} 1

1 - 2v

sin ² в

не обращается в нуль, поэтому ранг системы равен четырем, она имеет единственное решение

^£п = ^{0 £} 22) = .¹ J¹ Q ^{, £} 22) = ^{0 £} 12 = 0.

1 - 2 v 1

Компоненты деформаций в особых точках подчиняются шести условиям, НДС здесь полностью определено.

• 2.3.    sin a* 0, sin в = 0, (в = п).

• 2.4.    sinα=0, sinβ=0, (α=β=π).

Случай аналогичен предыдущему. Компоненты деформации находятся по формулам

^£ 11 = ^{0 £} 22 = ^{0 £} 22) = —7T^ ^v 2T Q ^{, £} 12 = 0.

g (1 -v 2 )

Из уравнений (6) следуют два ограничения на компоненты деформации в вершине клина

1 - ν ₁ (1)

-

g (1 -ν ₂) (2)

ε 22 = Q . (1 - 2 ν ₂)

ε 11 = , ε 22 (1 - 2 ν ₁)

Еще два ограничения вытекают из равенств (5). Суммарное количество ограничений равно четырем.

3.    Частные случаи соединения элементов

Рассматриваются наиболее интересные, по мнению авторов, варианты геометрических параметров вблизи вершины клина: α =β,α+β=π/2,α+β=π,α+β=2π.

• 3.1.    α=β, sinα≠0 (случай sin α = 0 рассмотрен в п. 2.2, 2.4)

Определитель (8) преобразуется к виду

Δ= 2sin 2 α ( V - W sin 2 α ),                            (14)

где

• V ₌ ( g + 1)(1 -ν ₁) ₊ g ( g + 1)(1 -ν ₂) W ₌ g (1 - 2 ν ₁) + 1 ₊ g [(1 - 2 ν ₂) + g ] 1 - 2 ν ₁1 - 2 ν ₂,1 - 2 ν ₁1 - 2 ν ₂

Если определитель (14) не обращается в нуль, уравнения (6) имеют единственное решение вида (9), в котором Δ определяется равенством (14), а определители Δ _i вычисляются по формулам

Δ 1 =- 2(1 - g ) Q sin 4 α , Δ 2 = 2(1 + g ) Q sin 2 α cos 2 α , Δ 3 =- 2(1 + g ) Q sin 2 α cos 2 α ,     Δ 4 = Q sin 2 α sin2 α .

Параметры состояния в вершине клина подчинены шести ограничениям, НДС здесь полностью определено.

При выполнении накладываемого на материальные и геометрические параметры условия sin2 α=V/ W.

определитель (14) обращается в нуль. Равенство (16) определяет угол скрепления элементов 1 , 2 , при котором ранг матрицы системы уравнений (6) оказывается меньше четырех. Область существования такого угла в пространстве параметров ( g , ν 1 , ν 2 ) с учетом положительности величин V и W определяется неравенством

( g - 1)[ ν 1 (1 - 2 ν 2 ) - g ν 2 (1 - 2 ν 1 )] ≤ 0.

Если g = 1 , неравенство (17) выполняется независимо от значений ν 1 , ν 2 . При этом α=β=π/2 . Возможные случаи поведения решений уравнений (6) в зависимости от ν 1 , ν 2 приведены в п. 2.1.2.

Когда g ≠ 1 , неравенство (17), определяющее область существования угла α , удовлетворяющего условию (16), распадается на две группы неравенств g<1,

ν2 ≤

ν 1

2 ν 1 + g (1 - 2 ν 1 )

g > 1,

ν2 ≥

ν 1

2 ν ₁ + g (1 - 2 ν ₁)

.

Для некоторых значений g области, ограниченные неравенствами (18), (19) в плоскости ν 1 , ν 2 , представлены на рис. 2.

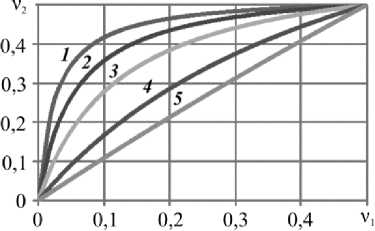
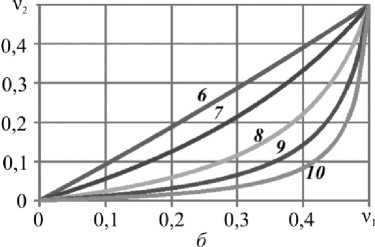
Рис. 2. Области существования решения уравнения (16) оказываются ниже кривой ( а ) в соответствии с (18) или выше кривой ( б ) в соответствии с (19) для значений параметра g :

1 – 0,05; 2 – 0,1; 3 – 0,2; 4 – 0,5; 5 – 0,9; 6 – 1,111; 7 – 2; 8 – 5; 9 – 10; 10 – 20

Fig. 2. Regions of existence for equation solution (16) are below the curve ( a ) in accordance with (18) or above the curve ( b ) in accordance with (19) for the value of parameter g:

1 – 0,05; 2 – 0,1; 3 – 0,2; 4 – 0,5; 5 – 0,9; 6 – 1,111; 7 – 2; 8 – 5; 9 – 10; 10 – 20

Для каждого сочетания материальных параметров, удовлетворяющего неравенствам (18) или (19), существует два угла α 1 и α 2 =π-α 1 , определяемые равенством (16). При α 1 и α 2 ранг системы уравнений (6) равен трем. Ее решение существует лишь при условии обращения в нуль всех определителей (15). Это возможно лишь при Q = 0 (см. п. 2.1). В этом случае из уравнений (6) следуют зависимости между деформациями

(1)      (2)      ε ₁₁ (1 + g ) ctg ² α _k

ε 22 = -ε 22 =-

=-^{ε 11 ctg α k} ,( k = 1, 2). 1 - g

Равенства (20) и (5) в сумме составляют пять независимых ограничений на компоненты деформаций в вершине клина. Когда выполняется условие Q ≠ 0 , ранг расширенной матрицы оказывается больше ранга матрицы системы. Уравнения (6) несовместны. В этом случае углы α 1 и α 2 следует считать критическими, так как при приближении сочетания материальных параметров к значению, удовлетворяющему (16), компоненты деформации в вершине клина неограниченно возрастают.

• 3.2.    α+β=π/2.

Определитель (8) преобразуется к виду

Δ=asin4α+bsin2α+c,

где

a = 2 ⁽ g - 1) ₁ .

1 - 2 v 1

-

)

1 — 2 v ₂

2(2 v . g ) ² g ⁽¹ - g ^v 2 ) 1 - 2 v 1          1 - 2v 2

_c = 2(1 -vj 1 - 2 v 1

Когда определитель (21) не обращается в нуль, решение уравнений (6) запишется равенствами (9), в которых А определяется равенством (21), а A i - формулами

А 1 = - 2(1 - g ) Q sin² a cos² а ,     А ₂ = 2 Q cos² a (cos² a + g sin² a ),

A 3 = - 2 Q sin² a (cos² a + g sin² a ),     A 4 = Q sin a cos a .

НДС в особых точках полностью определено. Коэффициент а в равенстве (21) обращается в нуль в двух случаях: когда g = 1 или когда безразмерные параметры задачи связаны соотношением g=

1 - 2 v ₂

1 - 2 v 1

При a = 0 определитель (21) обращается в нуль при условии b sin² a + c = 0 .

Если g = 1, а параметры v 1 , v ₂ удовлетворяют условию

v2 >--------,

² 3 - 2 v 1

существует решение a * уравнения (24). При a = a * ранг матрицы системы уравнений (6) равен трем. Определители (22) одновременно обращаются в нуль только при Q = 0, поэтому возможны случаи:

• 1)    Q * 0 . Ранг расширенной матрицы оказывается больше, чем ранг системы (6), эти уравнения несовместны. Угол a * является критическим углом скрепления элементов 1,2;

• 2)    Q = 0. Компоненты деформаций при a = a * в особых точках подчиняются ограничениям

£ 11 = 0,   е ⁽ ₂₂ = 2 £ ₁₂ctg a ,   £ 22) = - 2 £ ₁₂tg a .

Когда g * 1 и коэффициент а обращается в нуль вследствие зависимости (23), уравнение (24) решения относительно a не имеет.

Когда коэффициент а не обращается в нуль, исследование существования решений уравнения (21), подчиненных условию

0 <  sin² a <  1 ,

проводится в два этапа. Во-первых, в ортогональной системе координат v1, v2, g определяются непересекающиеся поверхности, удовлетворяющие условию b2 - 4ас = 0, g = gi(v1, v2), (i = 1,2,3,4),

определенные на множестве

0 1 <  0,5, 0 ₂ <  0,5.

Поверхности (26) упорядочиваются в соответствии с неравенством

⁰ <  g 1 <  g 2 <  g 3 <  g 4 .

Далее изучается существование решения уравнения А = 0 (согласованного с условием (25)) в точках поверхностей (26) и в точках ( v ₁, v ₂, g ), находящихся в пространственных областях между плоскостью g = 0 и поверхностью g = g ₁( v ₁, v ₂), между смежными поверхностями (26) и выше поверхности g = g ₄( v ₁, v ₂). В результате установлено, что в каждой точке множества (27) существует четыре корня: два корня в области между плоскостью g = 0 и поверхностью g = g ₁( v ₁, v ₂) и два корня выше поверхности g = g ₄( v ₁, v ₂). В точках поверхностей g = g ₁( v ₁, v ₂) и g = g ₄( v ₁, v ₂) корни совпадают между собой. Для примера все эти корни в случае v 1 = 0,4, v ₂ = 0,3 приведены на рис.3.

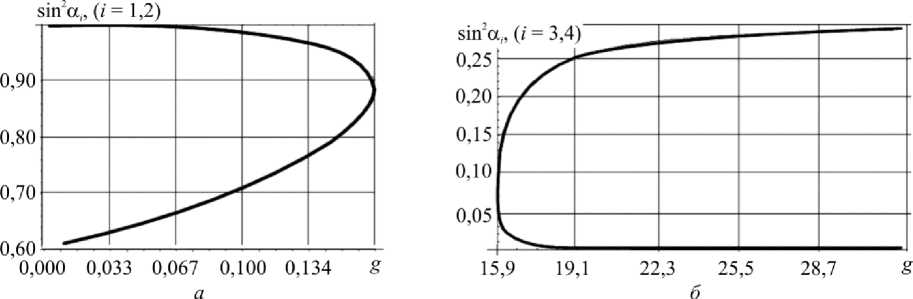
Рис. 3. Корни уравнения (21) в точке ( v ₁ = 0,4, v ₂ = 0,3) в зависимости от параметра g: а - в области 0 <  g <  g ₁( v ₁, v ₂); б - в области g >  g ₄( v ₁, v ₂)

Fig. 3. Roots of equation (21) at the point ( v ₁ = 0,4, v ₂ = 0,3) depending on parameter g: а - in the region of 0 <  g <  g ₁( v ₁, v ₂); b - in the region of g >  g ₄( v ₁, v ₂)

На поверхности g = g ₁( v ₁, v ₂) g (0,4; 0,3) = 0,167264 корни совпадают sin² а ₁ = = sin² a ₂ = 0,886721, на поверхности g = g ₄( v ₁, v ₂) g (0,4; 0,3) = 15,9428 корни совпадают sin² a ₃ = sin² a ₄ = 0,0758924. Данный пример показывает, что при фиксированных v ₁, v ₂ корни уравнения (21) существуют не при всех значениях параметра g . Если же сочетание материальных параметров v ₁, v ₂, g попадает в какую-либо из областей существования корней уравнения А = 0, то при Q * 0 имеется два угла скрепления элементов а ₁, а ₂ или а ₃, а ₄, которые следует считать критическими при температурной нагрузке, так как при таких углах система уравнений (6) оказывается несовместной. Если Q = 0 , ранг системы уравнений (6) равен трем, и между компонентами деформаций в особых точках оказываются справедливыми зависимости

£ ₁₁ = —^£ ₁₂ (1 — g ) sin 2 а , Е 2₂ = 2 £ ₁₂ctg а (cos² а + g sin² а ), £ 22) = - 2 £ ₁₂tg а (cos² а + g sin² а ).

• 3.3.    a + в = п, (0 < a < п).

Определитель (8) записывается равенством

А = - 2(1 - g ) sin² a(W 2 sin² a - V₂ ),

где

V = ^{1 -v} i - g ^{(1 -v} 2 )    W = g

² 1 - 2 v 1     1 - 2 v ₂ ’ ² 1 - 2 v 1 1 - 2v 2

Определитель (28) обращается в нуль при выполнении равенства g = 1 (случай рассмотрен в п. 2.2) или равенства sin2 a = Vr, (g * 1).                               (29)

W ₂

Если ни одно из этих равенств не выполняется, ранг матрицы системы уравнений (6) равен четырем. Она имеет единственное решение вида (9), в котором А определяется равенством (28), а определители А i вычисляются по формулам

А 1 =- 2(1 - g ) Q sin⁴ а , А ₂ = 2(1 - g ) Q cos² a sin² a , А ₃ = А ₂, А 4 = 0.        (30)

НДС в особой точке полностью определено.

Изучим существование решения системы уравнений (6) при выполнении равенства (29), которое накладывает ограничения на материальные характеристики

0 < V ₂/ W ₂ <  1.                                    (31)

Эти ограничения выполняются, если оказывается справедливой какая-либо из двух групп (32), (33) неравенств

v 2 <  g v 1 + 0,5(1 - g ),	v2<-----v------ , g + 2 v 1 (1 - g )
v 1 (1 - 2 g ) - (1 - g ) v<  , 2 2 v 1 (1 - g ) + g - 2 v 1 (1 - 2 g ) - (1 - g ) v >  , 2 2 v 1 (1 - g ) + g - 2	если g < / ? \),                   (32) 1 - 2 v 1 ) 2(1 -v, ) если g >-----—. 1 - 2 v 1 )
v 2 >  g v 1 + 0,5(1 - g ),	v 2 >v , g + 2 v 1 (1 - g )
^ х! ! - 2 ? ) -! 1 - ? ) v >  , 2 2 v 1 (1 - g ) + g - 2 v 1 (1 - 2 g ) - (1 - g ) v<  , 2 2 v 1 (1 - g ) + g - 2	если g <  .( 1 ),                       (33) 1 - 2 v 1 ) 2(1 -v, ) если g >----- —. 1 - 2 v 1 )

Для примера области существования значений углов a, удовлетворяющих уравнению (29), приведены на рис. 4 (серый цвет) в плоскости v1, v2 при некоторых фиксиро- ванных значениях параметра g.

В каждой точке области, определяемой неравенствами (32), (33), существуют два угла скрепления a 1 и a ₂ = п - a 1 , при которых ранг матрицы уравнений (6) равен трем.

Ранг расширенной матрицы зависит от значения Q. Если Q = 0, ранг расширенной матрицы совпадает с рангом матрицы системы. Между компонентами деформации оказываются справедливы зависимости s® = e22) = -2s11ctg2а, e12 = 0.

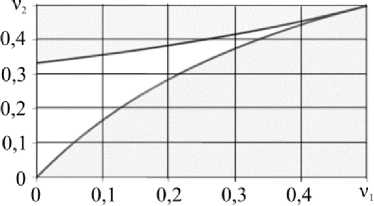
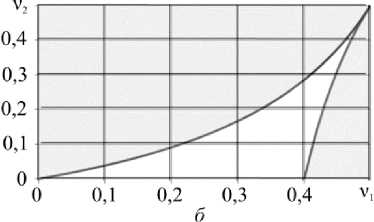
Рис. 4. Области существования решения уравнения (30) для различных значений g : а – g = 0,5; б – g = 3

Fig. 4. Regions of existence for equation solution (30) are for different values of g :

а – g = 0,5; б – g = 3

При Q ^ 0 ранг расширенной матрицы превосходит ранг матрицы системы, уравнения (6) несовместны. Углы а 1 и а ₂ являются критическими, так как особые точки в этом случае являются точками сингулярного поведения параметров состояния.

• 3.4.    а + в = 2п, (0 < а < 2п).

Определитель А в данном случае принимает вид (28), а A i ,( i = 1,2, 3,4) - вид (30). Определитель А (28) обращается в нуль при g = 1 (случай изучен в п. 2.2), при sin а = 0 (случай изучен в п. 2.4) и при выполнении условия (29). В последнем случае вследствие того, что а = п находится в области допустимых значений, вторые неравенства в группах (32), (33) не будут строгими. Вместо них получим соответственно

v 2 <

^v 1

g + 2vi(1 - g),

V2 ^

V1 g + 2V1(1 - g)

Кроме того, для каждого сочетания материальных параметров ( v 1 , v ₂, g ) из областей допустимых значений (исключая решение а = п , изученное в п. 2.4) существуют четыре угла а i ( i = 1,2,3,4), связанные равенствами

а1 = а*

а2 = п-а*

а3 =п + а*, а4 = 2п-а*,

а * = arcsin

,

при которых ранг матрицы системы уравнений (6) равен трем. Эти углы скрепления элементов 1 , 2 являются критическими, так как обусловливают сингулярность параметров состояния в особых точках при температурной нагрузке.

4.    Пример. Температурное нагружение составного клина с развернутым углом при вершине (а = р = п /2)

Случай описан в п. 3.3. В особой точке (точке А – вершине клина) (рис. 5) все компоненты деформации известны, они вычисляются по формулам (9) и (5). Количество заданных ограничений в особых точках избыточно, поэтому задача не является классической. Материальные параметры имеют значения: E 1 = 1,16 e 11 Па, V 1 = 0,3, © 1 = 0,11 e - 4град ^{- 1}, v ₂ = 0,35, w ₂ = 0,85 e - 5 град ^{- 1}. Модуль E ₂ варьируется, убывает, приближаясь к критическому значению E Кр = 0,7744 e11 Па . При E кр уравнение (29) имеет решения а * = п / 2 . Решение неклассической задачи при нагрузке A T = 100 °C строилось итерационным конечно-элементным методом, описанным в работе [20]. КЭ-сетка сгущалась к особой точке. Характерный размер 4угольного 8-узлового КЭ-элемента вблизи нее равнялся 2 мкм.

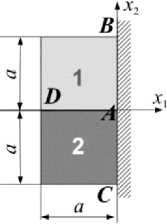
Рис. 5. Составной клин с развернутым углом при вершине, а = 1 см Fig. 5. Wedge with vertex angle, а = 1 cm

Решение в окрестности особых точек иллюстрируется на рис.6, где приведены напряже- ния c(2k) (к = 1,2) в окрестности особых точек при различных E2 на линии соединения элементов (рис. 6, а) и на линии заделки BC (рис. 6, б).

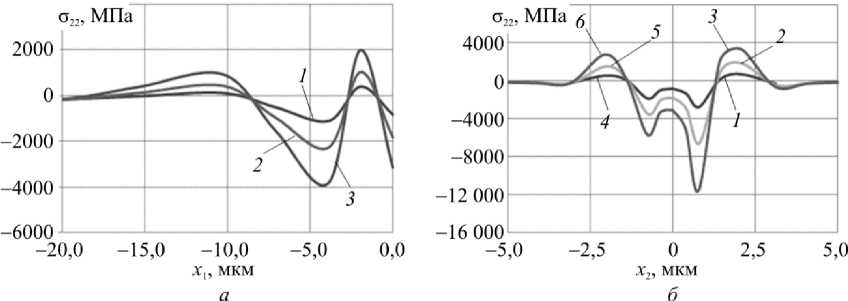
Рис. 6. Напряжения ст 2 к ) ( к = 1,2) в окрестности особых точек:

а - на линии соединения AD СТ 22) = ст 22) ; 1 - E ₂ = 80 ГПа; 2 - E ₂ = 82 ГПа; 3 - E ₂ = 88 ГПа;

б - по защемленному краю CB: 1 - ст^ ’ , E ₂ = 80 ГПа; 2 - ст 22’ , E ₂ = 82 ГПа;

(1)                                         (2)                                        (2)                                        (2)

3 - СТ 22 , E 2 = 88 ГПа; 4 - СТ 22 , E 2 = 80 ГПа; 5 - СТ 22 , E 2 = 82 ГПа; 6 - СТ 22 , E 2 = 88 ГПа

Fig. 6. Stresses ст 2 к ) ( к = 1,2) in the regions of singular points: а - at cross line AD ст 212) = ст 22)

1 - E ₂ = 80 ГПа; 2 - E ₂ = 82 ГПа; 3 - E ₂ = 88 ГПа; б - along fastened end CB:

1 - СТ 22) , E ₂ = 80 ГПа; 2 - ст 2¹₂⁾ , E ₂ = 82 ГПа; 3 - ст^ , E ₂ = 88 ГПа; 4 - ст 22) , E ₂ = 80 ГПа;

5 - ст 22) , E ₂ = 82 ГПа; 6 - ст ⁽₂²₂) , E ₂ = 88 ГПа

Выполняются все задаваемые для этих напряжений ограничения. Максимальными напряжения ст22 (к = 1,2) оказываются не в особой точке, а в малой ее окрестности. С приближением сочетания материальных параметров к критическому значению напря- жения неограниченно возрастают. Аналогичные результаты справедливы и для напряжений о([), о(2),(k = 1,2). На рис- 7 представлено решение рассматриваемой задачи для пе- ремещений.

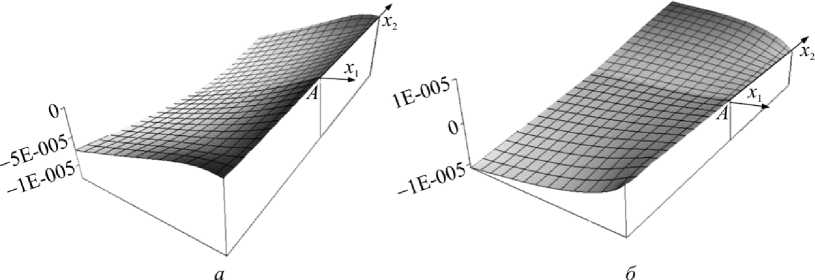
Рис. 7. Поверхности перемещений: а – u_{x 1} ; б – u_{x 2}

Fig. 7. Surfaces of dislocations: а – u ; b – u x ₁                x ₂

Видно, что они удовлетворяют граничным условиям (обращаются в нуль в заделке) и непрерывны на линии соединения составляющих пластинку элементов.

В таблице сравниваются с аналитическим решением напряжения в особых точках, вычисленные итерационным методом и методом конечных элементов (ANSYS).

Сравнение точного и численных решений в особых точках в элементах 1 , 2 конструкции ( E ₂ = 80 ГПа)

Comparing point and numerical solutions at singular points in elements of 1,2 construction (E2 = 80 ГПа )

Напряжения, ГПа	Точное решение		Итерационное		ANSYS-решение
	Номер элемента
	1	2	1	2	1	2
( k ) и 11	–5,58	–6,84	–5,62	–6,79	–0,0528	–0,0957
( k ) и 22	–3,11	–3,11	–3,13	–3,09	–0,138	–0,212
( k ) и 12	0,00	0,00	7,17-10 - 7	-5,92 -10 - 7	0,0990	0,146

Напряжения a ,2) ( k = 1,2), отвечающие итерационному методу, на семь порядков меньше максимальных напряжений в этих точках, поэтому естественно считать их равными нулю. Из таблицы видно, что итерационное решение задачи с достаточной точностью определяет напряженное состояние в особых точках. Значения всех напряжений непосредственно в особых точках, вычисленные в пакете ANSYS, в разы отличаются от точных значений (см. таблицу). Значительное отклонение ANSYS-решения от точного обусловлено тем, что классический подход не в состоянии построить решение, удовлетворяющее избыточно заданным ограничениям в особых точках. Вне окрестности особых точек радиусом 5–10 характерных размеров макроскопического представительного объема материала ANSYS-решение совпадает с итерационным.

Вычисления выполнялись на суперкомпьютере ТЕСЛА-ПГУ научно-образовательного центра параллельных и распределенных вычислений Пермского государственного национального исследовательского университета.

Заключение

В работе показано, что задачи МДТТ с особыми точками образуют новый класс задач, в которых количество заданных в этих точках условий переопределено и зависит от сочетания материальных и геометрических параметров, рассматриваемых элементов конструкций. Предлагаемый подход к изучению НДС в особых точках и их окрестностях позволяет построить задаваемые ограничения, изучить их, адекватно поставить задачу МДТТ; построить решение, согласованное со всеми задаваемыми ограничениями. Такое решение вне малой окрестности особой точки согласуется с решениями, получаемыми классическими методами. Это обстоятельство дает возможность оценить область вблизи особой точки, вне которой справедливо асимптотическое решение. Характерный размер такой области составляет пять-десять характерных размеров макроскопического представительного объема материала деформируемого тела. Проведенное исследование открывает перспективы для разработки методов исследования класса задач МДТТ с избыточно заданными ограничениями. Полученные результаты могут найти применение в механике композитов, механике разрушения и трещин.