Напряженное состояние диафрагмы трубчатого гидротехнического сооружения на просадочных грунтах

Введение. Напряженно-деформативное состояние элементов конструкций в большей степени зависит от распределения напряжений по контакту фундамента сооружения и его основания [2;3;4;5;6 и др.].

В практике проектирования контактные напряжения рассчитываются, исходя из представления о грунте как об изотропной упругой среде или, реже, из гипотез линейного распределения реактивных давлений грунта. Следует отметить, что расчеты, проведенные с применением различных гипотез, могут дать результаты, существенно отличающиеся друг от друга [1;7]

Распределение давлений в основаниях ГТС достаточно неравномерно и подвержено серьезным изменениям в процессе эксплуатации сооружений. Особенно ярко такая трансформация напряжений появляется при работе гидротехнических сооружений на неравномерно замачиваемых и сильно деформируемых просадочных грунтах [9;10;11;12].

Обзор научной литературы.

Значительное количество отказов и аварий типовых сетевых сооружений, имеющих причину отмеченные обстоятельством, указывает на необходимость дальнейшего совершенствования методов их проектирования этих сооружений, возводимых на лессовых грунтах [11;12;13]. Действующие в настоящее время нормативные документы [14;15 и др.] не учитывают влияние неравномерных просадок и увлажнения грунта на величину давлений по площади контакта сооружения с основанием.

Материалы и методы . В процессе исследований нами была подробно изучена работа трех трубчатых переездов, которые построены на просадочных лессовых грунтах на юге Узбекистана.

Ниже приводятся типичные эпюры реактивных усилий лессового грунта на давление диафрагмы трубчатого переезда – перепада, полученные в ходе экспериментальных исследований (рис.1 в, г, д, е). Наибольший интерес для дальнейшего анализа представляют эпюры, соответствующие периоду зависания диафрагмы на трубе, а также периоду частичного увлажнения основания диафрагмы. Именно в этих случаях экспериментальные эпюры реактивных усилий лессового грунта наиболее значительно отличаются от теоретических (рис. 1 а, б).

Теоретические эпюры

а ) Гипотеза линейного распределения реактивных давлений

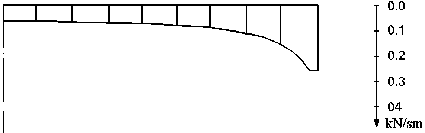
б ) Гипотеза опирания на упругое полупространство

Экспериментальные эпюры

в ) до начала замечания

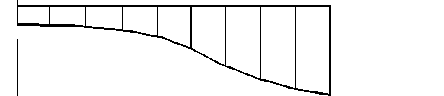
г ) 3 суток после начала замачивания

д ) 4 суток после начала замачивания

е ) 6 суток после начала замачивания

Рис. 1. Эпюры реактивных усилий грунта на давление от диафрагмы.

Будем считать, что диафрагма работает как монолитная конструкция. Это положение справедливо, если обеспечивается прочность швов, соединяющих отдельные плиты диафрагмы.

Наибольшие усилия в этих швах возникают в случае «зависания» диафрагмы на трубе. Усилие, воспринимаемое одним швом в этом случае будет равно:

N ш = Q 1 - P cp ·b·l (1)

где , Q 1 - вес крайней плиты диафрагмы, кН; Р ср - среднее контактное давление между крайней плитой и основанием; b -ширина плит диафрагмы, см; l 1 - длина продольной грани основания крайней плиты диафрагмы, см;

Для случая увлажнения грунта под всей диафрагмой оно может быть принято равным начальному просадочному Рср=Рнач, кН/см2;

Сила трения между плитами и грунтом как величина сравнительно малая и идущая в запас прочности в формуле (1) не учитывается.

Тогда требуемая площадь среза сварного шва, соединяющего плиты диафрагм будет равна:

N

F = ^ш , см² ш

Rs где, Rs- расчетное сопротивление н а с р е з м а т е р и ала шва, кН/см2.

Результаты и обсуждения. Если целостность швов, соединяющих плиты оголовка, обеспечена, то диафрагму можно приближенно рассчитывать как балку с больщим отношением h / b по схеме, представленной на рис. 2 и соответствующей периоду зависания диафрагмы (рис.1 д ).

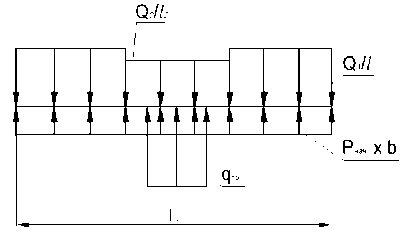
Рис. 2. Расчетная схема диафрагмы, соответствующая случая ее зависания на водопроводящей трубе.

С достаточной для практических целей степенью точности можно считать реакцию отпора грунта равномерно распределенной и равной Р нач . Исходя из выше изложенного, максимальный изгибающий момент в диафрагме для случая ее зависания на водопроводящей трубе будет иметь значение:

Q ( / 1 + I 2 ) ^{- Р} нач . в ( l i + ;2⁾²    QI -q (/2

M = ____________________2  + Q212  qTpdTp где,  l2-  длина продольной грани основания средней плиты диафрагмы, см; qтр- интенсивность реакции отпора трубы, кН/см2; Q2- вес средней плиты, кН; dт- диаметр трубы, см.

При l 1 = l 2 =l, что практически бывает часто, формулу (2) можно представить в следующем виде:

_M _ ^{1 2 (8} q 1 ⁺ q 2 - ^{9 Р} нач . в ^в - q Tp d Tp ) - q mp d t )² 1₈

где, q 1 =Q 1 /l 1 ; q 2 =Q 2 /l 2 .

В соответствии с положениями строительной механики, можно определить интенсивность реактивных усилий трубы:

2Qx + Q 2 - 3 Р нач Ь/

q mp =

dTp

Следует однако отметить, что приведенные формулы справедливы лишь в случае увлажнения грунта по всей площади контакта диафрагмы с основанием. На практике это соответствует действительности тогда, когда распространение воды по контакту диафрагмы с грунтом в сторону от оси сооружения отвечает требованию:

B + ( h + h_3Q4J1 ) tg e >  L ⁽³⁾

где, В - ширина замачиваемого участка, м; L - пролет оголовка – диафрагмы, м; β - угол растекания фильтрующей влаги и вертикали, для лессовых суглинков β =50⁰, для лессовых супесей, β =35⁰; Н - напор воды в канале, м; h загл – расстояние между нижней гранью диафрагмы и дном водоема.

Если это требование (3) не выполняется, то имеет место концентрация контактных напряжений под краями оголовка, опирающимися на неувлажненный грунт.

Расчетная схема, соответствующая такому режиму работы диафрагмы, приводится на рис. 3. Реактивные усилия неувлажненной части основания заменяем сосредоточенными реакциями А и В, что соответствует экстремальным условиям работы диафрагмы. Реакции А и В определяются обычным способом из уравнения равновесия системы.

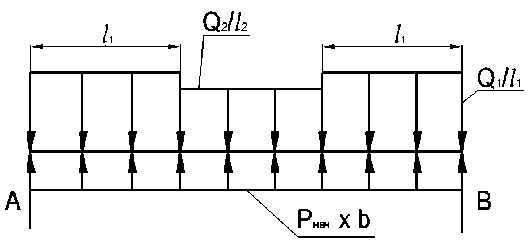
Рис. 3. Расчетная схема диафрагмы, соответствующая случая опирания ее краев на неувлажненный грунт.

Реактивным давлением трубы можно пренебречь, поскольку в этом случае оно пренебрежимо мало.

Максимальный изгибающий момент в середине пролета диафрагмы будет иметь следующее выражение:

M

(9 Р нач Ь1 + 4 Q 1 - 5 Q 2 ) l

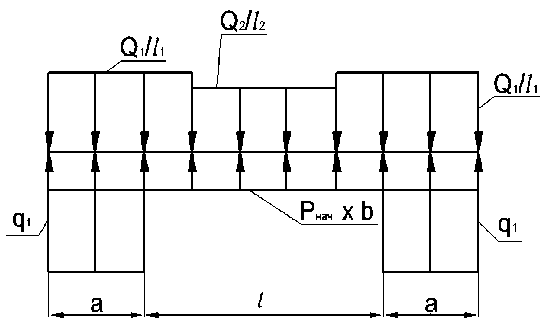
Рис. 4. Расчетная схема диафрагмы, соответствующая случая частичного увлажненный грунт.

Протяженность неувлажненного участка для массива грунта с установившемся контуром увлажнения может быть определена по формуле: a = L — B — ( H + * ™ * tg ^P             (5)

где, В- ширина зеркала воды в соответствующем     бьефе;     hзагл- расстояние между нижней гранью оголовка - диафрагмы и дном водоема.

Длина увлажненной части ℓ основания оголовка-диафрагмы будет ℓ = L – 2 а = 2 ℓ 1 + ℓ 2 - 2 а

В соответствии с расчетной

Приведенные формулы (2) и (4) соответствуют экстремальным режимам работы диафрагмы. Если же значительная часть основания диафрагмы не увлажнена, расчетная схема будет иметь вид, представленный на рис. 4.

схемой, представленной на рис.4.6, максимальный изгибающий момент в диафрагме равен:

M_; =

Q212 -PHQ4l2b , Q1( 11 +12)-qo(a +1)a где, q0 – интенсивность реакции неувлажненной части основания диафрагмы (н/см).

При ℓ1= ℓ2= ℓ, но при Q1 ≠ Q2 в диафрагме из трех плит момент м = Q^(2a - 5/) + 4Q1(a -l) + 3Рначв1 - 2a)

³                            8

Если разница в весе средней и крайний плит пренебрежимо мала, то формула принимает вид

M з = ^( V - Q )(3 l — 2 a )        (8)

Приняв в формуле (7) а = 0, вновь получаем выражение (8).

уменьшением а момент увеличивается, т.к. увеличивается разность ( 3ℓ-2а ).

Формулы (6), (7) и (8) и справедливы в том случае, когда нагрузка на неувлажненную часть основания не достигает величины, превышающей ее несущую способность. В противном случае произойдет скалывание неувлажненного грунта под краями оголовка (рис. 5).

Как видно из формулы (7), с

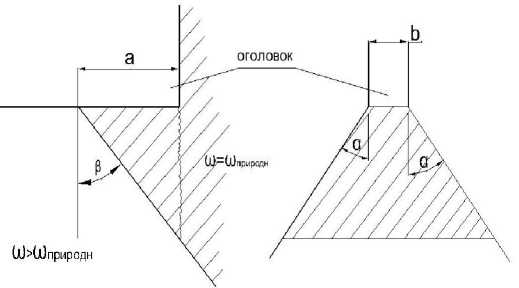
Рис. 5. Схема опирания оголовка-диафрагмы на неувлажненый клин грунта.

Площадка сдвига может быть представлена в виде равнобедренной трапеции с верхним основанием равным толщине диафрагмы . Высота трапеции, в соответствии с принятыми на рис. 5 обозначениями, равна h = α / tgβ.

Нижнее основание трапеции имеет размер:

b = b + 2 htga = b + 2atga tgP где, α - угол рассеивания давлений в грунте от действия дополнительной нагрузки.

Исходя из этого площадь трапеции будет равна:

b + b     ab  a ² tg a

F,-a = () h =+ cd ^v 2 ⁷     tg p    tg ² в

Принимаем    с    некоторым допущением,    что    вес    плит воспринимается        увлажненным лессовым грунтом по всей площади основания диафрагмы.

Разность между весом диафрагмы и суммарной реакцией отпора увлажненного грунта соответствует нагрузке на площадки сдвига под обоими краями диафрагмы. Его значение может быть определено по результатам лабораторных испытаний грунтов. Для лессового маловлажного грунта С = 0,005÷0,05 МПа.

2Q. + Q 2 - P_Ha4b (2 / 1 + / 2 ) = 2 F cd c

(9) где, С - удельное сцепление грунта природной влажности.

Внутренним трением грунта пренебрегаем как величиной сравнительно малой, что идет в запас прочности.

Выразив Fсд через параметр «а», найдем его граничное значение, при котором будет справедливо выражение (6).

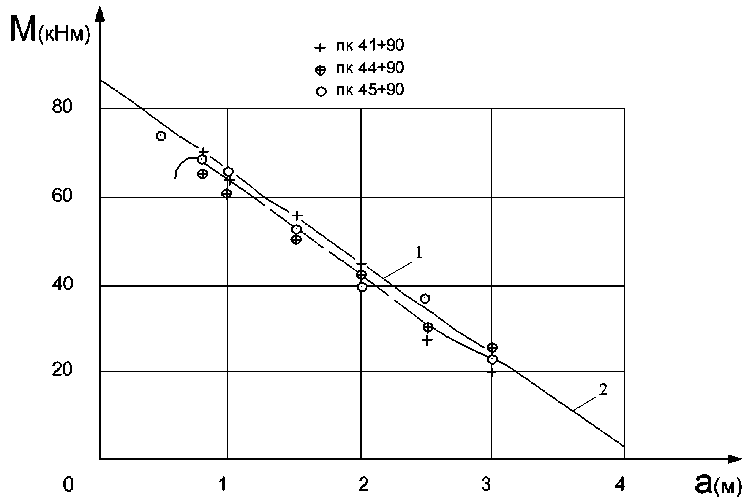
Рис. 6. Графики изменения максималного изгидающего момента в оголовке переезда-перепада в зависимости от параметра "а": 1- по формуле (8); 2- по экспериментальным данным.

Q 1 + 0,5 Q 2 — Vl — 0.5 PJ 2 = abC + ""^               (10)

tg p    tg в

Для этого решаем уравнение относительно «а» , подставляя в него исходные данные для трубчатого перепада ПК 45+90, работа которого исследовалась в процессе эксперимента:

в =0,25м; С =40 кН/м²; Ш пр = 11%; Q 1 =50 кН; Q 2 =40 кН; Р нач =25 кН/м²; L =9 м;

В результате получаем значение а = 0,68 м.

Для сравнения на рис. 6 приводятся графики зависимости максимального изгибающего момента в диафрагме одноочкового перепада, подсчитанного по формуле (7) и определенного на основе экспериментальных эпюр контактных напряжений, от величины параметра «а».

Из рис. 6 видно, что большинство экспериментальных точек расположены ниже теоретической зависимости: средняя разность равна - 2,4 кНм, что составляет всего 3% в области максимальных значений изгибающего момента.         Среднеквадратичное отклонение экспериментальных точек от прямой составляет 5=2,7 кНм.

Экспериментально установлено, что скалывание неувлажненного грунта под краями оголовка происходит при значениях «а»  =  0,4^0,7 м, что достаточно близко к теоретически определенному    значению    этого параметра. После скалывания клиньев неувлажненного грунта напряжения на контакте диафрагмы с основанием будет соответствовать эпюре рис.1. г) и схеме на рис.2.

На внутреннюю грань оголовка перепада сказывает давление насыпной уплотненный грунт. Величина этого давления на диафрагму составляет:

q = ф-p-h   (11)

где,   ф-   коэффициент бокового давления; ρ- удельный все насыпного грунта,   кН/м3;   h - глубина от поверхности насыпи, м.

Расчетная     схема     работы диафрагмы в этом случае может быть ширинs с заделкой на уровне бетонного крепления дна канала (рис. 7).

представлена как консоль единичной

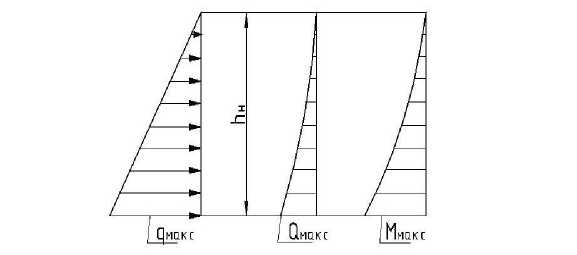
Рис. 7. Расчетная схема работы диафрагмы от навала грунта со стороны

водопроводящей трубы.

Надежность         закрепления обеспечивается значительной глубиной заделки и наличием жестко связанной с диафрагмой трубы.

Длина консоли соответствует высоте насыпи h н (рис. 7 и 8):

h н = h пл – h загл - h св                     (12)

где,   hсв–   высота части плиты диафрагмы,     находящейся     над поверхностью грунта. Примем hсв = 0, что идет в запас прочности.

Распределенная    по    закону треугольника нагрузка на консоль имеет максимальную интенсивность у заделки, которую можно определить для условной вырезанной полосы единичной ширины по формуле: q׳max= φρhн ,      кН/м              (13)

Максимальный изгибающий момент в диафрагме от действия навала насыпиого грунта возникает в сечении заделки q Л и ^ph 3Л m

M H (max) = ax H = ₆ ^H , кН/м ⁽¹⁴⁾

Выводы. Исходя из выше изложенного, следует заключить, что оголовки-диафрагмы трубчатых ирригационных сооружений, работающих на лессовых присадочных грунтах, могут находиться в различных условиях нагружения в зависимости от характера увлажнения основания и особенностей взаимодействия с водопроводящими элементами (рис. 89).

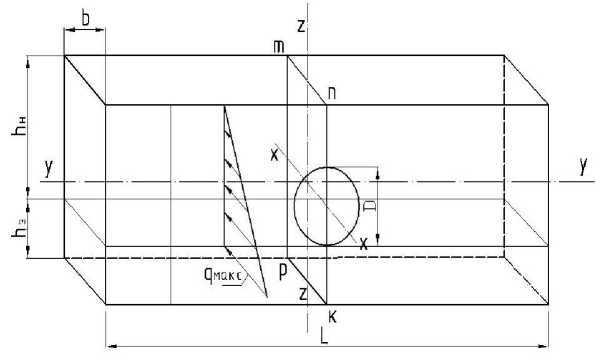
Рис. 8. Схема оголовка-диафрагмы трудчатого сооружения

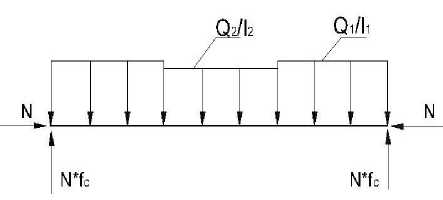
Рис. 9. Расчетная схема диафрагмы для случая навала грунта на ее боковые грани.

При этом, конкретное напряженное состояние оголовков зависит как от их массы и геометрических размеров, так и от физико-механических свойств и состояния грунтов оснований. Это указывает     на     необходимость определения на стадии проектирования наиболее опасного состояния диафрагмы в соответствии с предлагаемыми расчетными формулами и схемами.