Напряженное состояние двухслойной прямоугольной пластинки при сдвиге. Упрощенная двумерная модель

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2019PNRPU MECHANICS BULLETIN

Большинство математических моделей клеевых соединений внахлест, позволяющих описать напряженно-деформированное состояние соединения в аналитической форме, являются одномерными [1–5]. Другими словами, предполагают равномерное распределение напряжений по ширине соединения и априорно заданное распределение напряжений по толщине клеевого слоя и соединяемых слоев (как правило, равномерное или линейное). Данный подход успешно применяется для моделирования напряженного состояния двухсрезных клеевых соединений [6, 7]. Наличие симметричных накладок с двух сторон соединения позволяет уменьшить влияние изгибающих моментов в соединяемых слоях на напряженное состояние клеевого слоя.

Одним из направлений развития и уточнения математических моделей соединений является изучение распределения напряжений по толщине соединения, т.е. создание двумерных моделей соединения внахлест [8– 13]. При этом распределение напряжений по ширине соединения полагается равномерным. Однако при расчете напряженного состояния некоторых конструкций, например соединений силовых элементов или ремонтных накладок с обшивкой, необходимо учитывать неравномерность напряженно-деформированного состоя- ния склеиваемых пластин не только по длине, но и по ширине соединения. Как правило, для исследования двумерного напряженного состояния соединений используются различные численные методы, такие как метод конечных элементов или метод конечных разностей [14–20]. Аналитическое решение задачи о напряженном состоянии соединения в общей двумерной (в плоскости склейки) постановке пока не известно. В связи с этим для решения задач предложено две упрощенные модели, которые позволяют получить решение задачи в аналитической форме:

• 1)    для изучения влияния на напряженное состояние соединения поперечных деформаций, обусловленных коэффициентами Пуассона соединяемых пластин, касательные напряжения в них полагаются равными нулю [21–24]. Приложенная к соединению нагрузка в этом случае полагается равномерно распределенной вдоль боковых сторон пластинок, а соединяемые пластины полагаются абсолютно податливыми на сдвиг;

• 2)    для решения задачи о напряженном состоянии соединения при неравномерной нагрузке перемещения несущих слоев в плоскости соединения в поперечном направлении полагаются равными нулю, т.е. соединяемые пластины полагаются абсолютно жесткими в направлении, поперечном приложенной продольной нагрузке [25].

  Гипотеза об отсутствии поперечных перемещений ранее была использована при решении ряда задач для прямоугольных пластин и клеевых соединений (двумерная по толщине модель соединения) [9, 26]. В рамках этой модели также получено аналитическое решение задачи о напряженном состоянии клеевого соединения пластинок разной ширины [27]. В перечисленных выше работах [25, 27] упрощенная двумерная математическая модель клеевого соединения была использована для описания напряженного состояния соединения, вызванного продольной нормальной нагрузкой (растяжение-сжатие). Однако клееные конструкции также могут быть нагружены касательными напряжениями в плоскости соединения [28–31]. Примерами таких конструкций являются соединения полок балок со стенкой балки, соединения панелей обшивки фюзеляжа или крыла самолета и т.д.

  Целью данной работы является построение аналитического решения и исследование напряженного состояния клеевого соединения внахлест прямоугольных пластин, нагруженных касательной нагрузкой. Данная задача в двумерной постановке решается впервые.

  1. Постановка задачи

  Рассмотрим клеевое соединение двух прямоугольных пластин ( a х b ), показанное на рис. 1. К противоположным боковым сторонам у = 0 и у = b приложена сдвиговая

  нагрузка. Торцы x = 0 и x = а свободны от нагрузки. Обозначим толщины первого и второго несущих слоев б, и б₂ соответственно. Толщину соединительного слоя обозначим б₀. Считаем, что несущие слои деформируются только в плоскости соединения (плоскости x 0 y ), клеевой слой работает только на сдвиг, и напряжения равномерно распределены по толщине слоев.

  
  

  также будут равны нулю. Уравнения равновесия элементов несущих слоев в данном случае имеют вид [16, 25]

  
  

  д N  д q        д N₂   д q

  т +    - +   ¹ = 0, —т +   - +  - = 0,

  д x   д у         д x    д у

  
  
  
  

  где N , q – нормальные (в продольном направлении) и касательные усилия в несущем в слое k , k = 1, 2; τ – касательные напряжения в клеевом слое в продольном направлении.

  Соотношения Коши при условии равенства нулю поперечных перемещений имеют вид

  
  

  N k = б k E k ^U , q_k =б _kG_k ^ UE , k = 1,2,    (2)

  д x             д у

  
  

  где U – продольные перемещения слоя k .

  Напряжения в клеевой прослойке полагаем пропорциональными разности перемещений слоев:

  
  

  т =

  
  

  G ( U 2 — U 1 ) , ^б 0

  
  
  
  

  где G – модуль сдвига клеевого слоя.

  Подставив приведенные выше соотношения в уравнения (1), получим систему

  
  

  <

  
  

  а - '/   + Ц     1 — U - + U - = 0,

  ( д x       д у )

  Гд ² U   ₂ д ² U ) _{тт тт} „

  а      + ц      + U — U = 0,

  2      2      12

  ( д x        д у )

  
  
  
  

  Ek бД      G

  где ^а k = -^-;; ц k = J ; ^k = ^1,2.

  Краевые условия на торцах имеют вид

  4 k ( 0, у ) = 4 k ( а , у ) = 0, т.е. с учетом (2)

  
  
  

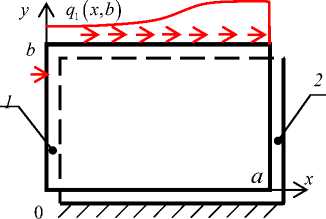
  Рис. 1. Схема клеевого соединения

  
  

  6 2    б ₀   б .

  
  

  д U_k

  ^{д x} x = 0

  
  

  = 0.

  x =

  
  
  
  

  /77

  
  

  Fig. 1. A scheme of the glued joint

  Полагаем, что а >  b , и изгибом пластин в плоскости соединения можно пренебречь. Поскольку поперечные (в направлении оси y ) перемещения несущих слоев считаем равными нулю, усилия в поперечном направлении и соответствующие касательные напряжения в клее

  
  

  На боковых сторонах заданы либо перемещения

  
  

  ^Uk\_y =0 = ^v t^{)( x} ) ^{;   U}k\_y = b = v k ^{2)( x} ) ,            ⁽⁶⁾

  
  

  либо касательные усилия

  
  

  -fi^ U qk |у =0    ^Gk ⁶ k ^

  
  

  q k\ _y = b    ^G k ⁶ k

  
  

  = Q k ( x ) ;

  x =0

  
  

  = Q k ²⁾( x ).

  
  
  
  

  2. Построение решения

  Из первого уравнения системы (3) следует, что

  
  

  U 2 = U 1

  
  
  
  

  f5 ² ц    ₂ 5 ² ц 1

  ^ttl  ----7  + Ц ---- 7    .

  ¹ 1 5 x ^{2      1}   5у ² J

  
  
  
  

  Подставив (8) во второе уравнение системы (4), найдем

  
  

  г ц     -   _-

  И Д 4   '" ■-•-’ ^+в 3 а 4

  5 x      5 x 5 у      5 у

  
  

  —

  
  

  Уравнение (11) решим методом разделения переменных. Частные решения уравнения будем искать в виде Ф ( x , у ) = X ( x ) Y ( у ) . После подстановки в уравнение (11) и удовлетворения граничных условий (14) получим

  с ,² X" _  с ²Y Y "- Y

  X "    Y ’

  
  

  5 ² Ц

  5 x

  
  

  —

  
  

  5 U л Y 2^" = 0, 5 у

  
  
  
  

  X '( 0 ) = 0; X '( a ) = 0.

  
  

  где в ₂ = a , a ₂,    в ₂ = a , a ₂ ( ц 2 + ц 2 ) ,   P 3 = a ₁ a ₂ ц 2 ц 2 ,

  Y 1 = a , + a ₂, y₂ = a^, + а₂ц₂ .

  Обозначим

  
  

  Поскольку обе части равенства зависят от разных переменных, то полученное равенство возможно только в случае, когда обе его части постоянны:

  
  

  с ,² X "

  X

  
  

  с ₂ ² Y "- Y

  Y

  
  

  -X ² .

  
  
  
  

  „   5² Ц    5² Ц

  ^Ф Y    + Y i^¹

  5 x      5 у

  
  
  
  

  и определим, при каких значениях коэффициентов c

  
  

  и c уравнение

  
  

  2 5Ф   2

  + с

  ¹ 5 x ^{2     2}

  
  

  5 2 Ф

  ■

  
  

  -Ф = 0

  
  
  
  

  эквивалентно уравнению (9). Подставим (10) в (11) и приравняем коэффициенты при производных в полученном уравнении коэффициентам уравнения (10), по- 22

  2     ^a,^a₂       2      аЛ/ т Ц , ^Ц 2

  лучим зависимости с , =-------, с ₂ =---₂------₂ , а

  a,+a₂       ац + а₂ц₂

  f G  G 1

  также ц = ц₂  — = — . Последнее условие, очевид-

  1    ² I E ,    E 2 J

  
  

  но, ограничивает область применения предлагаемого метода решения. Однако если соединяемые материалы одинаковы (что характерно для сэндвич-панелей и ремонтных накладок) или же обладают близкими коэффициентами Пуассона, то предложенный подход оправдан. Обозначим ц = ц₂ = ц . В таком случае получим с₂ = ц с ,. Выражение (10) можно представить в виде

  
  

  \ f 5 ² U    2 5 ² U _t 1

  ^Ф = (^а1 ^+a2)1 —г- + ц -у-т I .         ⁽¹²⁾

  V 5 x       д у J

  
  

  Перемещения второго слоя (8) соответственно представим в виде

  
  

  ц = ц —^a 1 ф . a, +a₂

  
  

  Учитывая краевые условия (5), из соотношения (12) следует

  
  

  5Ф

  5 x

  
  

  5Ф

  5 x

  
  

  = 0.

  
  
  
  

  В результате получим спектральную задачу

  
  

  X "  + УУ X = 0,

  c ₁

  X ' ( 0 ) = 0; X ' ( a ) = 0.

  
  
  
  

  Система собственных функций данной задачи будет иметь вид

  X„ x            п пс^

  X n ( x ) = cos ——, где X n =---^, ( п = 0,1,2,... ) .

  
  

  Из второй части равенства (15), учитывая, что

  
  

  X = X_n , получим уравнение Y n "-

  
  

  ( "+xУ

  
  

  Y n = 0, решени-

  
  

  ем которого является семейство функций

  
  

  ^Y n ( у ) = A n ^cosh

  
  
  
  
  

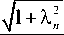
  с-)

  V ²

  
  

  ^у

  J

  
  

  f

  
  

  + B_n cosh

  
  

  с-i

  V ²

  
  

  ⁽ у ^- b )

  J

  
  

  Следовательно, общее решение уравнения (11) можно представить в виде

  
  

  №

  ^Ф ( x , у ) = E [ A n ^cosh ( ^ п у ) ⁺

  n = 0

  
  

  + B n cosh ( ^ n ( у - b ) ) ] cos ⁿ nx ,           ⁽¹⁷⁾

  
  

  ^/"+^XF

  где c, _n =-------; A_n , B_n - семейства произвольных

  c ₂

  
  

  коэффициентов.

  На следующем этапе построения решения необходимо найти общее решение уравнения (12). Решение будем искать в виде линейной суперпозиции решений V и W :

  
  

  ц = V + W ,                (18)

  
  

  где V является общим решением однородного уравнения (12) с однородными граничными условиями (5),

  
  

д² V 2 В¹ V _ --Г- + Ц -- у = 0.

В х ²       B y ²

Функция W представляет собой частное решение неоднородного уравнения (12), соответствующее заданной функции Ф ( х , у ) (17).

Решение уравнения (19) также будем искать методом разделения переменных. Искомую функцию представим в виде произведения V ( х ; у ) = X ( х ) Y ( у ) . Операция разделения переменных приводит к уравнениям

X " + Л ² X = 0, Y"--_т Y = 0 ,         (20)

Ц где -Л2 (Л > 0) - параметр разделения переменных.

Общее решение первого уравнения (20) при условии Л >  0 имеет вид

X ( х ) = С ₃ sin Л х + C ₄ cos Л х .

Функция X ( х ) удовлетворяет однородным граничным условиям (5) и не равна нулю тождественно только при Л_п = п па ^{- 1} ( п = 1, 2, 3,... ) . Таким образом, получим

X ( х ) = cos ( п а ^{- 1} пх ) .

Решение второго уравнения (18) при Л = Лп будет иметь вид

^Yn ( У ) = ^Сп cosh ( ^Л п Ц^{- 1} У ) ⁺ D n ^cosh ( ^Л п Ц^{- 1} ( У ^{- Ь} ) ) .

Если же параметр разделения переменных Л равен нулю, то общие решения уравнений (19) представляют собой линейные функции от координат x и y . Однородные краевые условия (5) в этом случае будут удовлетворены, если X ( х ) = const . Следовательно, решение уравнения (18), которое удовлетворяет краевым условиям (5), можно записать в виде

X

V = C 0 у ⁺ D 0 + £ ( C n cosh ( х п У ) ⁺ п =1

+Dncosh(хп (у - ь)))cos—, пп где хп = —;

ц а

C , D – семейства произвольных коэф- фициентов.

Функция Ф в уравнении (12) имеет вид (17), после некоторых преобразований частное решение (12) можно представить в виде

U k = C 0 у ⁺ D 0 ⁺ d k ( A 0 ^cosh ( § 0 у ) ⁺ B 0 ^cosh ( § 0 ( у ^{- Ь} ) ) ) ⁺

• ⁺    2 ^cos — [ C n ^cosh ( х п у ) ⁺ D n ^cosh ( х п ( у - ^Ь ) ) ⁺ п = 1        а

• ⁺    d k ( A n cosh ( § п у ) ⁺ B n cosh ( § п ( у ^{- Ь} ) ) ) ] ,     ⁽²¹⁾

где к = 1,2; d 1 = -c ¹— , d ₂ = c —^- .

а+а   а+а

Касательные усилия в несущих слоях (2) имеют вид 9 k = ⁵ k^Gk [ C 0 ⁺ d k § 0 ( A 0 ^sinh ( § 0 у ) ⁺ B 0 ^sinh ( § 0 ( у ^{- Ь} ) ) ) ] ^{+ + 5} k G k 2 ^cos ^ ^^ Гх n ( C n ^sinh ( х п у ) ⁺ D n ^sinh ( х n ( у - ^Ь ) ) ) ⁺ n = 1        a

• ⁺    d k § n ( A n ^sinh ( § п у ) ⁺ B n ^sinh ( § n ( у ^{- Ь} ) ) ) ].     ⁽²²⁾

Краевые условия (7) разложим в ряд Фурье по собственным функциям задачи (16) на интервале ( 0; а ) , получим

Q 1 ( ^х ,0 ) =0 , Q 1 ( ^х , ^ь ) = ^а 0-+ 2 ^а п cos ^{п пх},

2    п=1

U2 (х,0) = 0, Ql (х,Ь) = 0,(23)

aa где а0 =- [q^  х) dx, ап =- [q^  х) cos a   aa

Удовлетворив краевым условиям (7), получим системы линейных уравнений относительно коэффициентов A_n , B_n , C_n , D_n :

• ' C 0 - d 1 § 0 B 0 sinh ( § 0 Ь ) = 0,

C 0 ^{+ d} 1 § 0 A 0 ^sinh ( § 0 ^Ь ) =        ,

• <                              ^{2 5} 1 G 1

D 0 ^{+ d} 2 ( A 0 ⁺ B 0 ^cosh ( § 0 ^Ь ) ) = ⁰ ,

C _o + d ₂§₀ A sinh ( §₀ Ь ) = 0.

хnDn sinh (хпЬ) + d1§nBn sinh (§пЬ) = 0, хnCn sinh(хпЬ) + d 1§nAn sinh(§пЬ) = ^^7,

• <                                                 ⁵ 1 G 1

2. ^cos — а, + а_{2 п} = ₀      а

C n ⁺ D n ^cosh ( х п^Ь ) ^{+ d} 2 ( A n ⁺ B n ^cosh ( § п^Ь ) ) = ⁰ , х n C n ^sinh ( х п^Ь ) ^{+ d} 2 § n A n ^sinh ( § п^Ь ) = 0.

Решения систем (24) и (25) запишем в виде пп

W = —c-

^Х [ A n cosh ( § п у ) ^{+ B}n cosh ( § п ( у - ^Ь ) ) ] .

На основании (12) и (17) получим

1                 a ₀

2 ^ 0 5 1 G_i ( d ₂ - d 1 ) sinh ( Д b )’

в клеевом слое при равномерной касательной нагрузке. При этом слагаемые, стоящие под знаком суммы, опи-

1 d ₂                a ₀

0 “ 2 d_x ^ G ( d ₂ - d_x ) sinh ( Д b )’

сывают напряжения в клее, вызванные самоуравнове-

шенной нагрузкой,

поскольку

D

ad

C = -

0    2 5j G ( d ₂ - d_x )

a n nx cos--- dx = 0

0 ^a

при

n = i, 2,3,.... Можно показать, что в глубине области,

1 d₂   a о ( d 2 cosh ( ^ 0 b ) - d - )

2 d " ^Д G ( d ₂ — d ) sinh (Д b )'

An =

an

Cn = —

^ n ⁵ - G i ( d i - d 2 ) sinh ( ^ o b ) ; a n ^ n d 2

x n ⁵ - G i ( d i - d 2 ) sinh ( x n b ) ;

________________did2an (^n51 Gi (d- -d2))"_________________. d2Xn sinh(xnb)cosh(^nb)- dЛn sinh (^nb)cosh (xnb) ’ d2an sinh(xnb)(5iGi (di -d2)sinh(^nb)) i drn sinh(^nb)cosh(xnb)-d2xn sinh(xnb)cosh(^nb)

при удалении от краев у = 0 и у = b , слагаемые, стоящие под знаком суммы экспоненциально убывают, что совпадает с принципом Сен-Венана. То есть если соединяемые пластины будут достаточно велики, то на удалении от края напряженное состояние соединения будет мало зависеть от конкретного распределения нагрузки по краю и будет определяться лишь суммарной a величиной нагрузки a0 = — j Q^2 (x) dx.

a ₀

3. Численный пример

Из приведенных формул следует, что A , B , C , D :

^{H [ a} n ^]                 1

: ——¹—, где H I a_n I - некоторые линейные выра- n^R ( ^ n ; x n )

жения с постоянными коэффициентами, зависящие от an (22), a R (^n; xn ) = {sinh(^nb); sinh(xnb)}• Следова

Рассмотрим клеевое соединение двух алюминиевых пластинок, имеющих размеры a = 6 см, b = 2 см, 5 = 3 мм, 5₂ = 2 мм. Толщина клеевой прослойки 5₀ = 0, i мм. Упругие характеристики материалов соединения E_x = Е ₂ = 70 ГПа, G = C 2 = ²⁷ ГПа, G = 0,5 ГПа. Зададим следующие краевые условия на боковых сторонах склеенных пластин:

q i ( x , b ) = F ( x ) , q i ( x ,0 ) = q 2 ( x , b ) = 0 ; U 2 ( x ,0 ) = 0,

тельно A n , B n , C n , D n ~^7;;, где ⁵ - ² . Таким n s^R ( ^ n ; x n )

cosh (%„ у) образом, гиперболические функции             , sinh (xnb)

^cosh ( x n ( У ^{- h} ) )     ^cosh ( ^ п У )

,               и т.д. на интервале sinh (xnb)        sinh (^nb)

у е ( 0; h ) ограничены и экспоненциально стремятся к нулю с ростом n . Учитывая сказанное выше, можно сделать вывод, что внутри рассматриваемой области ряды Фурье (20) дважды дифференцируемы и удовлетворяют уравнениям (4). А ряды (21) и (22) на отрезке у е [ 0; h ] сходятся равномерно.

Касательные напряжения в клее (3) можно представить в виде где

F ( x )

<

F 0 ,

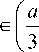
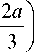
0, x е

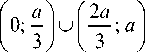
График касательных напряжений в клее приведен на рис. 2. Напряжения на рисунке показаны в безразмерном виде как отношение действующих напряжений τ к гипотетическим напряжениям τ0, которые возникли бы при равномерном распределении нагрузки по всей плоскости клеевого шва, т.е. как отношение τ к напря-a1   F жениям т„ = F---= — .

⁰⁰ 3 ab 3 b

T =--а'   G0 [Ao cosh (^0У ) + B0 cosh (^0 (У - b))] - а + а2 50

О-i G n       П nX

--i--0 > cos----X а, +а2 50 П=-     a

^X^ A n cosh ( ^ n y ) + B n cosh ( ^ n ( у ^- b ) ) ] .

Можно отметить, что в данной формуле слагаемые, стоящие вне знака суммы, представляют собой известное одномерное решение [30] и описывают напряжения

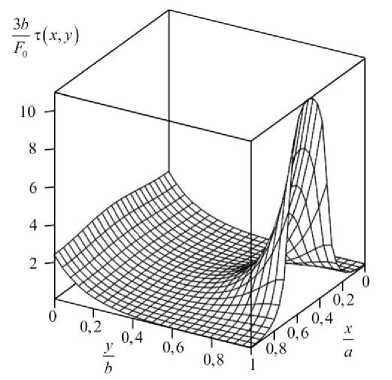
Рис. 2. Касательные напряжения в клеевом слое

Fig. 2. Shear stresses in the adhesive layer

Для верификации предложенной методики проведен расчет напряженного состояния соединения при помощи метода конечных элементов (МКЭ) в пакете COMSOL Multiphysics 5.3. Для расчета использована трехмерная модель, генерация сетки автоматическая, характерный размер элемента 0,03 мм.

На рис. 3 приведены графики касательных напряжений в середине толщины клеевого слоя вдоль оси симметрии соединения ( x = a /2), вычисленные при помощи предложенной методики ( а ), и МКЭ ( б ).

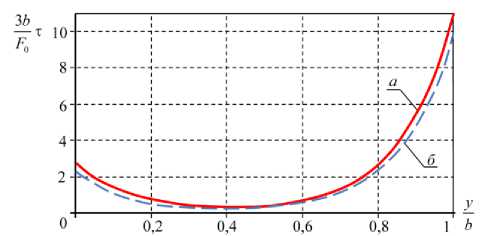
Рис. 3. Касательные напряжения в клее вдоль прямой x = L / 2 : а - расчет по предложенной методике; б - МКЭ

Fig. 3. Shear stresses in the adhesive layer along the line x = L /2 : а - calculation by the proposed method; b - FEM

0 '           O',2         0Д 0^6          0^8 I' a

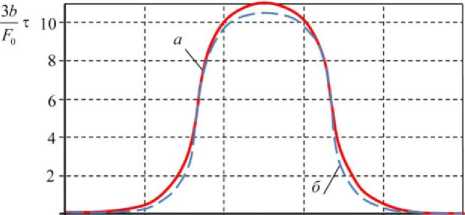
Рис. 4 . Касательные напряжения в клее вдоль прямой y = h : а – расчет по предложенной методике; б – МКЭ

Fig. 4. Shear stresses in the adhesive layer along the line y = h : а – calculation by the proposed method; b – FEM

На рис. 4 приведены графики касательных напряжений в серединной плоскости клеевого слоя вдоль края y = b , вычисленные при помощи предложенной методики ( а ), и МКЭ ( б ).

Из графиков видно, что касательные напряжения в клее, вычисленные по предложенной модели, несколько превосходят напряжения, вычисленные при помощи МКЭ. Расчет напряженного состояния данного соединения при помощи МКЭ также показал, что касательные напряжения в клее в поперечном направлении, которые обусловлены поперечными перемещениями слоев и которые в предложенной модели не учитываются, не превосходят 9 % от максимальных касательных напряжений в продольном направлении.

Заключение

Предложена упрощенная модель клеевого соединения, которая позволяет находить напряженное состояние соединения при произвольном нагружении соединяемых пластин касательными усилиями на боковых сторонах. Получено аналитическое решение задачи и обоснована его сходимость. Решена модельная задача.

Расчеты показали, что точность предложенной приближенной методики достаточна для решения многих инженерных задач. Данный подход может быть использован для построения аналитических решений задач о напряженном состоянии клеевых соединений деталей разной ширины; соединений силовых элементов конструкции с обшивкой; соединений, которые имеют дефекты в клеевом слое; соединений ремонтных накладок с обшивкой и других задач, где требуется знать двумерное напряженное состояние клеевого соединения.