Напряженное состояние и разрушение адгезива при соединении пластин внахлест

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2024PNRPU MECHANICS BULLETIN

Исследование прочности соединений в слоистых композитах связано с нахождением напряженно-деформированного состояния их адгезионных слоев (АС) [1–3]. В силу того, что толщины АС существенно уступают толщинам сопрягаемых ими материалов, вводится несколько моделей представления АС. Одна из моделей рассматривает АС в виде слоя нулевой толщины. Дефект слоя в этом случае представляется трещиной Гриффитса с сингулярным полем напряжений, формирующим критерии в виде J-интеграла или удельной упругой энергии [4–8]. Основным недостатком данной модели является формальное исключение реальных механических свойств адгезива из описания деформирования композита.

Вторым, более естественным подходом является рассмотрение адгезивов с реальными толщинами. В этом случае одним из основных методов решения является конечно-элементное моделирование деформирования композита [9–13]. При этом исследуются как напряжения по массиву адгезива, так и напряжения по границе соединения адгезива с несущим телом на основе когезионных элементов [14–16]. Наряду с численными методами используются и аналитические представления, полученные в рамках тех или иных допущений [17–20], основанные на теории балок и пластин [21–22].

Одним из широко исследуемых адгезионных соединений является соединение внахлест, или single-lap bonded joints (SLJ) [9–12; 16–20; 23], показанное на рис. 1.

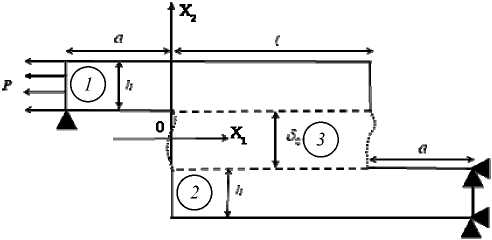
Рис. 1. Схема нагружения соединения внахлест

Fig. 1. Lap joint loading scheme

В этом случае два одинаковых тела 1 и 2 сопрягаются адгезивом 3 на участке длиной £ . В рамках упругого деформирования рассматриваемого композита наиболее известные аналитические результаты получены в работах [17; 18]. В работе [17] использовалась концепция «дифференциального сдвига», согласно которой тела 1 и 2 работают только на растяжение, благодаря которому в адгезионном слое 3 реализуются однородные по толщине сдвиговые деформации. Однако модель [17] не учитывает изгиб конструкции, благодаря которому в слое 3 наряду со сдвиговыми формируются и отрывные напряжения в направлении оси X2. Данный эффект был рассмотрен в работе [18]. Отметим, что коэффициент Пуассона в слое полагается нулевым. Влияние упругопластического деформирования адгезива в рамках его сдвиговых деформаций было рассмотрено в [24]. В работах [17; 18; 24] пренебрегалось напряжением в адгезиве вдоль оси действия внешней нагрузки. Его учет в постановочной части задачи был рассмотрен в [25], а влияние соответствующего напряжения на переход в пластическое состояние адгезива показано в статье [26].

Построение аналитических решений [17; 18; 26] связано с известным допущением относительно деформации ε 22 , которой пренебрегается, по сравнению с другими плоскими деформациями. В данной работе, как и в работе [27], предлагается учесть ее влияние в упрощенном аналитическом решении на формирование отрывных напряжений в адгезионном слое SLJ соединения на основе общей постановки задачи сопряжения двух тел посредством тонкого слоя [28]. Полученное решение сравнивается с решениями [17; 18] и конечно-элементным решением в рамках общей вариационной постановки задачи.

Отметим, что напряженное состояние в тонком слое, сопряженном на определенном участке с деформируемыми телами, в классических решениях [17; 18] определяется по полю его граничных перемещений. В этом случае граничные условия на торцевой свободной поверхности не ставятся, и напряжения на торце слоя определяются из найденного поля перемещений, что приводит к известным противоречиям, связанным с присутствием вектора напряжения на свободной торцевой поверхности слоя. В силу этих ограничений в данных решениях не прослеживается кромочный эффект [29] вблизи угловой точки свободной поверхности адгезионного слоя, связанный с тождественным выполнением условий свободной поверхности.

Постановка задачи

Следуя работе [28], запишем условия равновесия тел 1 и 2 в виде системы вариационных уравнений для тела 1 :

J о ■ ^£ ds + j 0 22 5 u + dx , + S             i

I        d 5 u + , _r

+ 0.55₀   o_n---- ¹—dx_l + I

I        s x ,

| g125 u+ dx1 + i

- 35 u + , ¹ г i „ ⁽¹⁾

o12-----dx1 = P ■ 5 u dl dx     J и тела 2:

J о ■ 5 ds - J 0 22 5 u 2 dx ₁ - J o ₁₂ 5 u ₁ dx ₁ +

S2                 i n s 1 г — 35 u,

^+0.55 0 I ^O 11 я

I , d x 1

i

-             ,(2)

35u2

o ₁₂— 2 dxx = P ■ 5 u dl ,

3x)

1 L ₂

где S k , k = 1,2 - площади тел 1 и 2 ; u - векторное поле перемещений в телах 1 и 2 ; σ , ε – тензоры напряжений и деформаций; σ , ε – тензоры средних напряжений и деформаций слоя с компонентами:

1 0,5δ 0

⁰ 11 ( ^x 1 ) = Г J ^o 11 ( ^x 1 , ^x 2 ) ^dx 2 ,

⁵ 0 - O,55 o

1 0,5δ 0

0 ₂₂ ( x ₁ ) = — J o ₂₂ ( x ₁ , x ₂ ) dx ₂ ,

⁵ 0 - O,55 o

1 0,5δ 0 o ₂₁ ( x ₁ ) = o ₁₂ ( x ₁ ) = — J o ₂₁ ( x ₁ , x ₂ ) dx ₂ , ⁵ 0 - O,55 o

^£ 22 ^{( x} 1 ) =

I u + ( x ₁ ) - u ₂ ( x ₁ ) I

I        $0

_f11 ( x _{1 )}= 0,5 I^ u ^+^2 x 1 1 ,

I dx1

^£ 21 ^{( x} 1 ) = ^£ 12 ^{( x} 1 ) =

= 0,5

u + ( x ₁ ) - u ₁ ( x ₁ )

δ 0

0 5 1 d u + ( x ₁ ) d u ₂ ( x ₁ )

, I 3x3

,

где u k - компоненты векторов перемещений верхней и нижней границ слоя соответственно; L _k – граница приложения внешней нагрузки для тела 1 и 2. Постулируется жесткое сцепление между границами области 3 и областями 1 , 2 .

Средние напряжения в слое связаны с его граничными напряжениями условиями равновесия, которые приводят к следующей взаимосвязи [28]:

_±                 do11 _'

• o12 = o12 + 0,550 - , o22 = o22 + 0,550 - , (5) dx1

±± где σ12 , σ22 – компоненты тензора напряжений на верхней и нижней границе слоя соответственно. Используется условие равенства компонент граничных напряжений слоя и напряжений на соприкасающихся к слою поверхностей тел 1 и 2. Достижение граничных компонент критических значений на отрыв и сдвиг может рассматриваться в качестве критерия отслоения адгезива от несущего тела.

Примем определяющие соотношения в форме закона Гука с нулевым коэффициентом Пуассона:

^oik = E ^k ,                      ⁽⁶⁾

где E - модуль упругости тел 1 и 2 ; i = 1,2.

Для материала слоя взаимодействия 3 определяющие соотношения считаем справедливыми для средних компонент тензоров напряжений и деформаций:

^o ik = ^E 3 ^£ik ,                         ⁽⁷⁾

где E ₃ – модуль упругости адгезива.

Для учета влияния деформаций консоли рассмотрим подход, аналогичный [30], однако в качестве неизвестных функций введем функции ψk , отвечающие за растяжение – сжатие консолей вдоль оси X2 [27], а не угол поворота материальных нормалей к срединной поверхности. Распределение перемещений в консолях при данном нагружении принимаем в следующем виде uk (X1,X2 ) = u±(X1),(8)

• ^u 2 ( ^X 1 , ^x 2 ) = ^u 2 ( ^X 1 ) + V k ^{( X} 1 ^{)( X} 2 + ⁵ 0/ 2 ) .

В этом случае деформацию консолей будут определять компоненты тензора деформаций:

dQ121

--+ 0,550

dx1

dM 1²2 dx ₁

21,       + 0,550       = -°22, dx1           dx1

- Q 222 = 0,

для участка x 1 е ( t ; t + а ] :

^Q = 0, ^Q = 0, ML - Q j₂ = 0,

22 dx ₁          dx ₁          dx ₁

с условиями сопряжения:

^11 (X1,X2 )   U1 , ^22 (X1,X2 )   Vk , ek2 (x1,x2) = 0,5 (u±' + vk' (x2 + 50/2

u +|

u +1 , u +        — u + , Vil A— Vil _ft,

¹ 1 x 1 —+ 0 ² 1 x 1 —- 0      ² 1 x 1 —+ 0 ^Y1 ^ —- 0 ^Y11 x 1 —+ 0’

При распределении деформаций в консолях в виде (7), (8) работа внутренних напряжений в теле 1 будет равна:

Q ₁1₂

1 x 1 — 0

Q 11|      =( Q 11 + 0,55 0 ° 11 )| ,

1 x 1 —-0     X                       /1 x 1 —+0

^{— ( Q} 12 ^{+ 0,55} 0 ° 12 )|      ^, M 12 I   ₀ ^{— M} 12 [ _₊₀

\                     /| x 1 —+ 0         ^1 —- 0           1 x 1 —+ 0

S 1

. , г' h + + ⁵0/²1 _ d ⁵ u + . _ X ' ^{5 £} ds =J J_S/2 °        ⁺ ° 22 ⁵ (V 1 ) ⁺

J - a •^,5o/² /       dx 1

+ ° ₁₂ 5 ( u 2 + + V 1 ' ( x ₂ - 5 ₀/ 2) ) ) dx 1 dx ₂ ,

u — u , u 9       — u 9

¹ 1 x 1 — 1 - 0       ¹ 1 x 1 — t + 0 ² 1 x 1 — 1 - 0       ² I.

^V 2 1 x 1 — 1 - 0 ^{— V} 2 1 x 1 — 1 + 0 ^,

I x 1 — 1 + 0

а в теле 2 :

f i     Г^{t +} a f^-5o/² I       d 5 U

I о ■ ■ o s ds =                 o..-----¹

S 2               ^{Jo    J}- ^h - ⁵ o/ 2 ^ ¹¹ dx 1

+ ° ₁₂ 5 ( u - + v₂ ' ( x ₂ + 5 ₀/ 2 ) ) ) dx 1 dx ₂ .

2- + G 22 ⁵ ( V 2 ) ⁺

¹                      (11)

( Q /1 + 0,55 0°_п )|       — Q 1²J

'                       ²1 x 1 — t - 0           1 x 1 — 1 + 0

^{( Q} 12 ^{+ 0,55} 0 ° 12 )|       = ^Q 12 I __h0 ^,

'                          'I x 1 — 1 - 0            ^lx 1 = t + 0

M 12 L- 1 0 ^— M 12l-(₊₀, 1 x 1 — t - 0              1 x 1 — t + 0

Введем в рассмотрение обобщенные силы и моменты:

1      p h + 5o/2                 1      p h + 5o/2

^Q 11 = J ₅0/ 2 °^{H dx} 2 , ^Q 22 = J ₅0/₂ ° 22 ^dx 2 ,

,       p h +5₀/2                     ,       p h +5q /2       /              . x

Qn = J _5o/2 ° 12 dx 2 , M 112 = J _5o/2 ° 12 ( x 2 - 5 o/ 2 ) dx 2 ,

естественными граничными условиями на левом и правом торце тела 1 :

Q ₁1₁

— Q 1 — Ph , Q d     — 0, M 12 1

I x 1 —- a                      I.

— 0,

2 Г-5o/2                    2      г—5o/2

^{Q 11} = J - h - 50/2 ° 11 ^{dx 2} , ^{Q 22} = J - h - 50/2 °^{22 dx 2} ,

- 5q /2                              - 5q /2

Qn = J - _h - _5o/2 ° 12 dx 2 , M 122 = J - _h - _5o/2 ° 12 ( x 2 + 5 o/ 2 ) dx 2 .

Проинтегрировав по частям ряд слагаемых, содержащих производную от вариации функций u f и v _k в (1), (2), (10), (11), и приравняв слагаемые при равных вариациях, приходим к системам дифференциальных уравнений для участка x 1 е [ - а ;0 ) :

( Q 11 + 0,55 0°_п )| _x 1 _{— t} — 0, ( Q 12 + 0,55 0 ° 12 )|

M 12 L (—^0, 1 x 1 — t

— 0,

^d Q = 0, dQ = 0, M- - Q / = 0,     (12)

22 dx ₁          dx ₁          dx ₁

и граничными условиями на торцах тела 2 :

(Q121 + 0,550°11 )|    — 0, (Q122 + 0,550°12 )| x                         71 x1 —0          x                          /|x1 —0

M 122 L -0— ^0, 1 x 1 — 0

— 0,

для участка x 1 е ( 0; t ] :

u -I — 0, u ₂'I       — 0, V2I , — 0.

¹ 1 x 1 — 1 + a              ² 1 x 1 — 1 + a            ^T2 ^1 ' • a

dQ 1¹1          d σ 11         dQ 1¹2          d σ 12

--+ 0,55_п----- = °-,,,--+ 0,55_п------ = °-, 9 , 021     0    22

dx ₁ dx ₁ dx ₁ dx ₁

dM 1¹2 dx ₁

- Q 22 = 0,

С учетом выражений (9) определяющие соотношения (6) получим в виде:

° k — Ed' , ° k₂ — E , ° k₂ — 0,5 e(u ₂ ^: '+ V ' ( x ₂ + 5₀/2 )) . (24)

¹¹        dx ₁

Запишем выражения обобщенных сил и моментов с учетом (23):

' u + — C ₁₀ e ^{1 1 X 1} + C_n e ^{в 1 1 X 1} + C ₁₂ e ^{1 3} x ¹ + C ₁₃ e

■ ¹3 ^X 1 I

+—C7X] +—Cc

du. ±                           I             1

Qk = !h     Q222 = Ehvk, Qk = 0,5EI u±h ± Vk hr I, dx1                           ^           2 J

(                 1

M ₂ = 0,5 E ± u ± — + v к — .

12               2 ₂ k ₃

Из (7), (3) и (4) получим связь средних напряжений в слое взаимодействия с его граничными перемещениями:

, +

в $ C.

⁸ 2 Eh ⁹

C — в C ₁₀ e ^{1 1 X 1} в C" e

+—C7Xi +—Cc

⁺       m2-  X 1

^u 2 ^10 a e λ ₁

λ₁ x ₁

в C ₁₂ e ^{1 3 X 1} в C ₁₃ e

^{δ 0} C ; 2 Eh ⁹

-C mE e-

C ₁₁ e λ ₁

— I

■ ¹3 ^X 1 I

■ ^1 ^x 1 + c ^m14 e ¹ 3 ^X 1 12 λ ₃

°n =

11 2

о ₁₂ = 0,5 E 3

dx ₁

+

I u

E'   .+

, ° 22    j ( u 2

δ ₀

в u

u 2 ) ,

δ 0

0,5 ( u ₂ ⁺ '

' Hl.

Таким образом, система дифференциальных уравнений (12)–(15) с учетом связей (25), (26) является замкнутой относительно шести неизвестных функций u 1 ⁺ ,

I u ₁ , u ₂ , u ₂ ,

, +

ψ ₁ , ψ ₂ . Каждая искомая функция входит

в систему со второй производной включительно. Четыре участка интегрирования системы приводит к двадцати четырем постоянным интегрирования. Удовлетворение двенадцати граничных условий (20)–(23) с учетом двенадцати условий сопряжения решений (16)–(19) даст решение поставленной задачи.

Решение задачи

Аналитическое решение для участка x 1 е [ в a ;0 ) с учетом граничных условий (20) запишем в виде:

u

Q ₁

Eh ^{1 +} C ^{1 ;}

К u

= C

² Eh ²

+

’ _в c ^h Г _e 2^6 ( ^x 1 ^{+ 2} a ) / h + _e

^{2 3} 2 L

; (27)

V — C 3 [ e ^{276 ( X 1 + 2 a} ) / ^h + e ^в:

Решение для участка X ' е ( / ; / + a ] с учетом граничных условий (23) имеет вид:

К

^u — ^— Ei: ^{[ X} 1 ^{1 1 + a} ) J ^C 4 ;

u В — Eh [ X 1 в ( / + a ) ] C 5 + C 6 2 [ e x" h v , — C 6 ^[ e 2^6^{X | /} h в e 2 ^{6 [} 2 a ' h I .

e -2^6 [ x , в 2 (П a ) ] / h ^ _;(28)

Решение для участка x 1 е ( 0; / ] :

-C m y. _е^в13 ^X 1 + —с X + ex

¹³ λ ₃           Eh ^{9 1}

e"^X 1         6^1 ^X 1         c ^{3 X} 1

⁺ 2^ 14 ⁺ ^15 e   ⁺ H6 e    ^{+ c}17 e   ^{+ c}18 e

в s~t          Ai Xi     s~t          в 1 Xi , s~t          1 Xi u 2 = C10 m15 e 1 1 в C11 m15 e  1 1 + C12 m16 e 3 1

^C 3 ^m16 ^e

■^{13 X 1} + — C„x. +

Eh ^{9 1}

2 C 14 в C 15-

-C _P ^вw ^X 1

C 16 e

—

μ₃ x ₁

;

μ 3 x 1

17 e 18 e

— I

μ₃ x ₁

;

m¹¹- ^1 ^x 1         ^{m     1} 1 ^x 1                   ^x 1

^V1   H0 A e H1 A e    ⁺ ^12 A e

λ ₁ λ ₁ λ ₃

в Cm e ^{в 1} з ^X 1 +

13 λ ₃

^{+ C} 15 ^m 17 e " ^{1 + C} 16 ^m 17 e "  ^{1 + C} 17 ^m18 e ^{И 3 1 +}

^{+ C} 18 m 18 e

— I

μ₃ x ₁

;

V 2 = C 10 m 19 e ^{1 1} x ^{1 в C} 11 m 19 e

^C 13 m 20 e

■ ¹3 ^X 1 I

+ C '₅ m '7 e ^Ц x ¹ + C '6 m '7 e

⁺ C 18 m 18 e

где m 1 =

E 3

■^{11 X 1} + C ₁₂ m ₂₀ e ^{1 3 X 1}

— I

■^Ц1 x ¹ + C ₁₇ m ₁₈ e³ x ¹ +

в

μ₃ x ₁

;

E 3

Eh ³ 2 Eh + 5 ₀ E 3

m - ⁽2E ₊ $0 E 3- mm +

³ I h

λ 2

1 1

г I ; ^m 2 = $ 0 J

δ₀ E ₃ h Eh ²

E ₃ h

4 ( 2 Eh + 5 ₀ E ₃ ) ;

8 ₀ E ₃ h Eh ² 1_;

6 + 12 J’ d — (m1 + m3 + m2m4 )2 в 4m1 m3; 11 —

m1 + m 3 + m 2 m 4 +-	d
2
\ m1 + m 3 + m 2 m 4 в a	d

;

m 7 =

^ 4 =

	2	; 3 V	2
m 1	+ m 3 + m 2 m 4	в d~d        24	m 6 — в	24 E 3
	2	; m 5 h 2 ;		δ 0 Eh 2
12	16 E 3	m — 501 3 Eh + E 3	( 4 Eh 1	1 4
	'm v                 ; 8 δ 0 Eh
h ;		9        2      50	[ E 3	δ 0 λ 1

;

;

| ;

' 1 J

δ 0 λ 3

5„1 3 Eh E, ( 4 Eh 1, m₁₀ = + ^{3 10} 2 $ 0 I E 3

в 4 ( m 5 m₈

Ц 2 = ^в•

;

\m. + m,, в DD Im. + m,, в DD " 3 ^— у —2 !— ; " ^{4 —} у —2 !— ;

δ 0 λ 12 m 9 m i 1 — 11      2 E 3    δ δ Eh 2 λ m„ =------ 12     24 E 3 δ 0 λ 3 m 10	1 0 Eh 2 λ 1 3 δ 0 E λ 1     4    2 h λ 1 ; 24 E 3       E 3     h 1 1 3 I 24      I      12 m9 1. m ,, +. l h 2 1 1    1 J 11 Eh 2 J 1
mi 7 13      2 E 3 δ 0 Eh 2 λ 3 m 14 = 24 E 3 4 Eh λ m is =-----1 — 15      E 3 m _ И2 — m 8 . m 17               . m 7 m — 1 2 m 20 =     - ' m 2 λ 3	δ 0 Eh 2 λ 3 3 δ 0 E λ 3 4   2 h λ 3 ; 24 E 3       E 3     h 1 3    3 1 24 3     12 mw 13 m 13 +. l h 2 1 3    3 J 13 Eh 2 J 4 m       4 Eh λ   4 m ---12 . m^ =-----14 δ 0 λ 1 λ 116       E 3 δ 0 λ 3 λ 3 22 цд — ms         m, — 1,    m, 38     11   11 m 18               . m 19         , + . . m 7              m 2 λ 1     λ 1 m 13 . λ 3

σ 22

Q 1 h c 2 Δ

L 32 K             3  k1X1

\ 1R 1--+ 1K cosh 1 cos 1 cosh---cos l 2 2

I 2 K               3     ^{1 X} . ¹ X

+ R. 1--+ 1K sinh 1 sin 1 sinh---sin--- l 12

где X = x ₁ — 0,5 / e [ — 0,5 / . 0,5 / ] .

2(/\

Eh δ ₀ ^;

, (33)

G 3 = 0,5 E 3 . c = 0,5 / .

cosh ( U₂c ) sinh ( Ua )

K =--------------- _     ----------- .

sinh ( U 1 a ) cosh ( U ₂ c ) + 2V2 cosh ( U 1 a ) sinh ( U ₂ c )

U = 2\I Q . U = U^ . K ‘ = KU . P = 2^⁽- .

¹ hEh ² 4            ¹        E δ ₀

I ⁶ E ^h I i Y c

Y = 3 . 1 = — . R = cosh 1 sin 1 + sinh 1 cos 1.

l E 8 ₀ )          h ¹

Для нахождения восемнадцати постоянных интегрирования в (27)–(29) используем двенадцать условий сопряжения (16)–(19) и шесть граничных условий (21), (22). После определения постоянных интегрирования в результате численного решения системы линейных уравнений находим напряженное состояние в слое:

o„ = 0,5 E 3 C 7;

^O12 = ^C 10 m 21 e ^Л‘ x + ^C 11 m 21 e ’^ x ¹ + ^C 12 m 22 e x ¹ + ^C 13 m 22 ex ¹ .

* O₂₂ = C ₁₀ m23 e^{1 1} x ¹ - C11 m23 e ^{— 1 1} x ¹ + C ₁₂ m24 e ^{1 3} x ¹ - C ₁₃ m24e ^{— l} 3 x ¹ +

+ C ₁₅ —³ e¹

15 δ0

2/?

+ C ₁₆ —³ e ^{- g1} x ¹

δ0

2/?            2/?

+ C ₁₇ —³ e ^g3 x ¹ + C ,_s —³ e

17 δ0

δ0

,- И 1 ^x 1 .

где

m 21 =

E 3 E 3 I 4 Eh 1 2 5;⁺т l “ E r

^^^B

δ

m 22

E 3 E 3 ( 4 Eh 1 2 4 'I --+               —      .

8 0    4 l E 3      5 o J

R ₂ = sinh 1 cos 1 — cosh 1 sin 1.

A = 0,5 ( sinh ( 21 ) + sin ( 21 ) ) .

Рассмотрим распределение поля напряжений в адгезионном слое при критической внешней нагрузке, полученной в экспериментальном образце согласно работе [16] со следующими геометрическими и механическими характеристиками: a = 83,75 мм, / = 12,5 мм, E = 70,1 ГПа, E 3 = 4,89 ГПа, 8 ₀ = 0,2 мм. В качестве материала консолей использовался алюминиевый сплав Al6082-T651, в качестве адгезива – смола Araldite AV138. Критическая нагрузка составила Q 1 = 0,24 МН/м.

На рис. 2 и 3 приведено сравнение решений (30)– (33). Здесь и далее напряжения отнесены к модулю напряжения сдвига (32) на торце слоя: о ik = о ik! |о₁₂ ( 0 )| , а координата x ₁ отнесена к длине адгезива / : x 1 = x 1 // . График 1 на рис. 2 соответствует решению (30), график 2 – решению (31), график 3 – решению (32).

m ₂₃

m 24

^E 3 I ² m 12

8 0 I 1 1

E 3 1 2 m ₁₄ 8 0 l 1 з

4 Eh λ ₁     4

E ⁺ 8Л

4 Eh λ ₃     4

“E T 8л

Наряду с полученным решением (30) приведем отличные от нуля компоненты напряжения в адгезионном слое решения [17]:

_     Q 1 w cosh ( wX // )

¹² / 2 sinh ( w /2 )

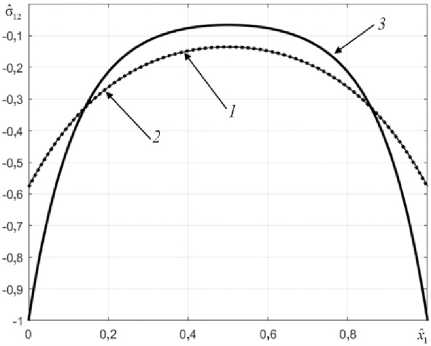
Рис. 2. Распределение напряжений сдвига по длине адгезива в рамках аналитических решений

и решения [18]:

^O 12

Q 1

8 c

& ( 1 + 3 K ) cose » h ⁴         sinh ( p c/h )

+ 3 ( 1 — K )

, (32)

Fig. 2. Distribution of shear stresses along the length of the adhesive within analytical solutions

Из рис. 2 видим совпадение решений (30), (31) и отличное от них практически в два раза на краях слоя решение (32).

На рис. 3 приведено распределение отрывных напряжений по длине слоя в рамках решения (30).

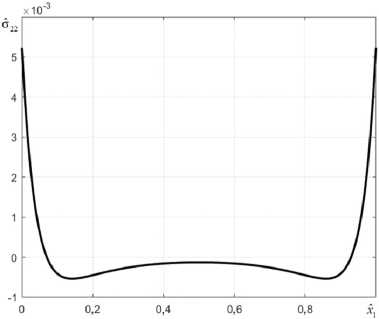
Рис. 3. Распределение напряжений отрыва по длине адгезива в решении (30)

• Fig. 3.    Separation stress distribution along the adhesive length in solution (30)

По представленному на рис. 3 распределению имеет место незначительное значение отрывных напряжений, порядка 0,5 %, от напряжений сдвига (32) на торцах слоя. Отметим, что для модели [17] отрывные напряжения тождественно равны нулю.

На рис. 4 и рис. 5 пунктирной линией показано распределение средних напряжений, полученных в рамках постановки задачи (1)–(7) методом конечных элементов (МКЭ) с квадратичным законом распределения поля перемещений на элементе. Непрерывной кривой показано решение в рамках модели [18] (32) и (33). График 1 и график 2 на рис. 4 соответствует напряжению σ ₂₂ , график 3 и график 4 – напряжению σ ₁₂ .

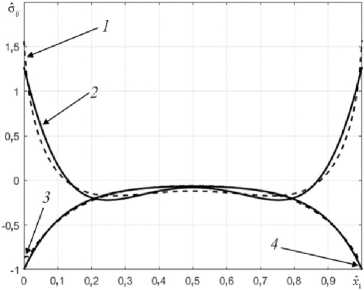
Рис. 4. Распределение напряжений отрыва и сдвига по длине адгезива

• Fig. 4.    Distribution of separation and shear stresses along the length of the adhesive

Из анализа распределений напряжений на рис. 4 видим, что средние напряжения отрыва на торцах слоя превосходят сдвиговые. Кроме того, решение МКЭ (1)–

• (7) дает большие по модулю значения напряжений отрыва и меньшее значение сдвиговых напряжений, по сравнению с решениями (32), (33), что подтверждается решениями МКЭ [19; 31] и связано с отсутствием учета деформации ε ₂₂ в несущих консолях модели [18]. Однако из сравнения решений рис. 2 – рис. 4 видим, что эффект от учета деформации ε ₂₂ незначителен, по сравнению с учетом изгиба консолей в модели [18], которая дает более близкие значения к решению 2D-задачи. Используя связи (5) для нахождения граничных напряже- ±

ний отрыва О 22 по изменению вдоль длины слоя средних касательных напряжений, получаем, что максимальные значения отрывных напряжений будут реализовываться на нижней поверхности адгезива при x 1 = 0 и верхней поверхности слоя на противоположном торце слоя.

Напряжения σ ₁₁ в моделях [17; 18] тождественно равны нулю. На рис. 5 приведено распределение средних напряжений вдоль оси Х 1 в рамках решения МКЭ (график 1 ) и решения (30) (график 2 ).

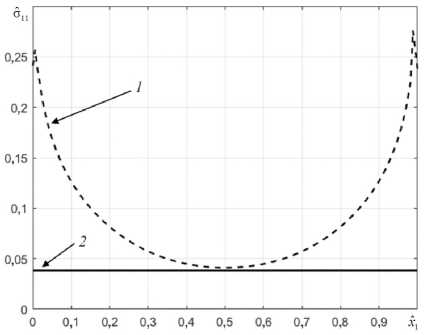
Рис. 5. Распределение напряжений σ ₁₁ вдоль оси Х 1 по длине адгезива

Fig. 5. Stress σ ₁₁ distribution along axis Х 1 along the length of the adhesive

Из анализа поведения решений на рис. 5 видно, что соответствующие напряжения в районе торцевых поверхностей адгезионного слоя в решении МКЭ практически в пять раз превышают напряжения решения (30).

Соотношение (5) при постоянном значении напряжений σ11 приводит к тому, что касательные напряжения по границам слоя о±2 равны средним. В этом случае при рассмотрении критерия отслоения адгезива по сдвиговым напряжениям верхние и нижние поверхности адгезива будут равноправны с позиции начала расслоения композита. Упрощенные решения (30)–(33) приводят к аналогичным результатам. Однако решение МКЭ при конечном значении толщины адгезива и существенной нелинейной зависимости напряжений в районе торцевых поверхностей слоя дает однозначный выбор поверхности отслоения адгезива. При этом если будет реализован сдвиговой крите- рий отслоения, то образование свободных поверхностей по (5) будет соответствовать отрывному критерию. Таким образом, если процесс разрушения адгезива определяется адгезионными связями с сопрягаемыми поверхностями, то процесс отслоения в рассматриваемом образце будет однозначно определяться одной и той же поверхностью вне зависимости от наступления сдвигового или отрывного критерия отслоения.

Заключение

На основе модели деформирования слоистого композита с тонким адгезионным слоем решена задача нагружения SLJ образца. Проведено сравнение извест- ных аналитических решений с конечно-элементным решением общей постановки 2D-задачи и с упрощенным решением, полученным на основе аппроксимации поля перемещений, учитывающей деформации растяжения – сжатия. Показано качественное соответствие найденного решения с решением в рамках теории пластин. Предложенная 2D-постановка задачи, в которой отсутствует сингулярность при конечной толщине адгезива, позволяет определить граничные по адгезионному слою напряжения взаимодействия с сопрягаемыми телами. Сопоставляя граничные напряжения с критическими напряжениями по отрыву и сдвигу, можно моделировать механизм отслоения адгезива от сопрягаемых им внахлест материалов.