Напряженное состояние нагруженного касательной нагрузкой неоднородного полупространства, не обладающего способностью воспринимать растягивающие напряжения



• 2)    две в шоры 5_ЭКС (при значениях к = оз/to = 1 и к = to to = И ) взаимно симметричны относительно эпюры со значением к, равным степени инверсии при соблюдении равенства

■^ЭКВ ^ ⁼ ^^ ⁼ 2 [^ЭКВ^ = 1) +

+-^экв^ = П)]; (22)

• 3)    оптимальной (и равномерной) следует считать эпюру при значении к = П, что равносильно соотношению

  

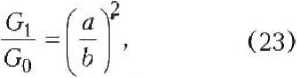
при котором 5'^х = 1,28р (в данном при мере). Очень важно, что равные напряжения (5ЭКВ = 1,2 р ) на наружной и внутренней поверхностях капилляра мало отличаются от величины 5™ВХ-

Таким образом, при всех других равных условиях наибольшей прочностью будет обладать такой капиллярно-пористый композит (с линейной неоднородностью), для которого соблюдается условие (23): к - П. Опасные точки, к тому же, располагаются внутри стенки капилляра (при р-0,75).

В заключение заметим, что приведенные выше рассуждения о прочности капиллярной ячейки справедливы и для неоднородной толстостенной трубы.

• 6 И Б Л И ОГРА Ф ИЧЕСКИЙ СПИ СО К

  • 1.    Андреев В. И. Некоторые задачи и методы механики неоднородных тел / В. И. Андреев. М. : АСВ, 2002. 288 с.

  • 2.    Светкина С. Н. Классификация деформаций ячейки капиллярно-пористого композита / С. Н. Светкина, А. С. Тюряхин // Актуальные вопросы строительства : материалы Всерос. науч.-техн, конф., посвящ. 40-летию строит, фак. Мордов. гос. ун-та. Саранск, 2002 Вып. 1. С. 342 — 346.

  • 3.    Светкина С. И. Упругие зависимости и эффективные модули жесткости капиллярно-пористых композитов / С. Н. Светкина, А. С. Тюряхин, В. Д. Черкасов // Проблемы строительного материаловедения : 1-е Соломатовские чтения : материалы Всерос. науч.-техн. конф. Саранск, 2002. С. 303 — 306.

  • 4.    Соломатов В. И. Макромеханика цилиндрической ячейки капиллярно-пористого композита / В. И. Солоиатов, В. Д. Черкасов, А. С. Тюряхин // Роль пауки и инноваций в развитии хозяйственного комплекса Республики Мордовия : материалы респ, науч.-пракг. конф. 27 — 28 марта 2001. Саранск, 2001. С. 283-291.

  • 5.    Черкасов В. Д. К определению пористости капиллярно-пористого композита / В. Д. Черкасов, А. С. Тюряхин, С. Н. Светкина // Современные технологии строительных материалов и конструкций : материалы Всерос. науч.-техн, конф., посвящ. 150-летию со дня рожд. акад. В. Г. Шухова. Саранск, 2003. С. 135-140

Поступила 05.04.05.

НАПРЯЖЕННОЕ СОСТОЯНИЕ НАГРУЖЕННОГО

КАСАТЕЛЬНОЙ НАГРУЗКОЙ

НЕОДНОРОДНОГО ПОЛУПРОСТРАНСТВА, НЕ ОБЛАДАЮЩЕГО СПОСОБНОСТЬЮ ВОСПРИНИМАТЬ РАСТЯГИВАЮЩИЕ НАПРЯЖЕНИЯ

Л. Е. ДУРАЕВ, кандидат технических наук

Касательная нагрузка q равномерно распределена вдоль прямой липин (рис. 1). В случае плоской задачи она дей- ствует па протяжении достаточной длины. Модуль упругости полупространства с глубиной z возрастает или уменьшается.

В общем случае закон изменения модуля упругости представим в следующем виде:

Е^ = Е„ + £_n eⁿz (_п< о), (1) где Е_ю — конечный модуль упругости на достаточной глубине, Е = Е_о - Е^, Е_о — модуль упругости на поверхности полупространства; в — основание натурального логарифма; п — показатель степени.

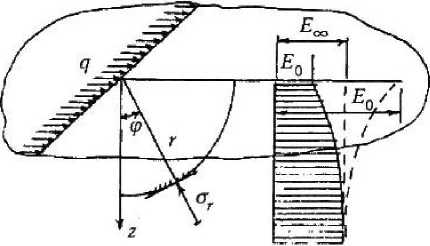
Р и с. 1

Природные (не скальные) грунты мало сопротивляются растягивающим напряжениям. В связи с этим грунтовый массив можно отнести к полупространству, рассматриваемому в настоящей работе. Тогда касательной нагрузкой можно считать, например, сдвигающие силы при работе грейдера или бульдозера.

На основании решения, представленного в [1], сжимающие радиальные напряжения а_г в цилиндрическом сечении на расстоянии г предлагаем определять по формуле

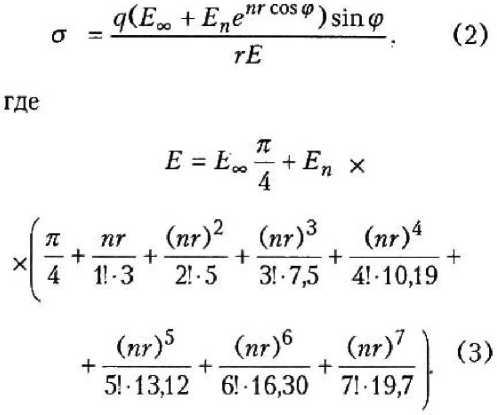
Значения параметров Е„, Ео, п мож но рассчитать по методике, предложенной в [2]. .

Пример 1. Модуль упругости на поверхности полупространства Е_о = = 30 МПа, на достаточной глубине Е^ = 50 МПа, п = -0,7. При этих параметрах имеем Е_п = Eq - Е„ = 30 - 50 = -20 МПа. Следовательно, модуль упругости возрастает с глубиной по закону

Е_(2> = 50 - 20 2,72 "<№ МПа.

Вычислим напряжения на расстоянии г = 1 м от места действия нагрузки q. Примем q = 1МН/м. По формуле (3) получаем;

Е = 50 —--20 х

<3,14 0,7 0,49 0,343

3    10    45

0,240 0,168   0,118    0,083 )

244,6 1 574 11 736 99 288 J

= 39,25-20(0,7854- 0,2333+0,0490 -

-0,0076 + 0,0001 -0,0001 +

+ 0,0000-0,0000) = 27,38.

Из выражения (2) имеем:

1(50 -20 -2,72’°’^7со^) sin <р

°т              27,38

При ф = 0 а_г - 0.

При ф = 0,45°

(50-20.2,72-°^). 0,707 = g

27,38

При ф = 90°

(50 -20 -гтГ^й А,0

а_г ----------------— = 1,096 МПа.

27,38

Эпюра напряжений представлена штрихпунктирной линией 1 на рис. 2. Для полупространства с постоянным модулем упругости (Е„ = 0)

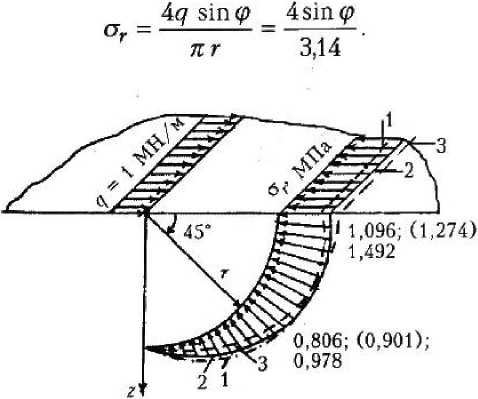
Р и с. 2

Эпюра напряжений для данного случая изображена сплошной линией 2 на рис. 2, числовые значения взяты в скобки.

Пример 2. После уплотнения верхних слоев полупространства (например, дорожного полотна) модуль упругости па поверхности Eq оказался равным 50 МПа, а ниже убывал в соответствии с выражением

E_U) = 20 + 30 -2,72"°'^7г МПа.

Вычислив по формуле (2) напряжения от действия нагрузки q = 1 МН/м, получаем эпюру напряжений <т_г, представленную штриховой линией 3 на рис. 2.

Как видно из рис. 2, напряженное состояние полупространства зависит от характера изменения модуля упругости. При возрастающем с глубиной модуле упругости величины напряжений в верхних слоях меньше напряжений в полупространстве с постоянным по глубине модулем упругости. В нижних слоях они имеют большую величину. При убывающем с глубиной модуле упругости в верхних слоях они больше, а в нижних — меньше.