Напряженное состояние в контактной прослойке опорной части с шаровым сегментом

Активно развивающейся областью механики деформируемого твердого тела является механика контактного взаимодействия [1]. Распределение контактных усилий между взаимодействующими деталями неизвестно и может быть найдено лишь в результате решения специфических задач, которые называются контактными задачами. В результате решения контактных задач могут быть сформулированы граничные условия на поверхности деформируемых тел, адекватные дей- ствительности. Представление о механике контактного взаимодействия дает ряд монографий [2], [3], [4] и [6].

Важными приложениями механики контактного взаимодействия являются задачи о напряженно-деформированном состоянии опорных частей пролетных строений мостов. С развитием технологий производства и появлением новых материалов с улучшенными физико-механическими свойствами произошла модификация конструкций опорных частей пролетных строений мостов. Представляет интерес изучение напряженно-деформированного состояния конструкций опорных частей и исследование поведения используемых в них современных материалов. Одним из основных и часто используемых типов опорных частей являются опорные части с шаровым сегментом.

В данной работе рассматривается задача контакта между ответственными деталями конструкции опорных частей пролетных строений мостов с шаровым сегментом. Опорные части с шаровым сегментом подразделяются на неподвижные, линейно-подвижные и всесторонне подвижные. Общими деталями опорных частей с шаровым сегментом (рис. 1) является верхняя плита с шаровым полированным сегментом – 1 , нижняя плита со сферическим вырезом – 2 и прослойка из антифрикционного материала (сферическая поверхность скольжения) – 3 .

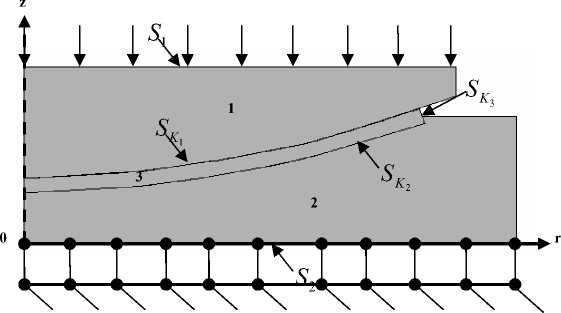
Рис. 1. Осесимметричная модель опорной части с шаровым сегментом

Исследуются две реальные конструкции опорных частей пролетных строений мостов с шаровым сегментом л-250 и л-350, отличающиеся радиусом шарового сегмента и соответственно радиусом сферического выреза (изготовлены ООО «АльфаТех» по проектам и с научно-техническим сопровождением ООО «Ко Люмьер Лтд», г. Москва).

1.    Математическая постановка

Общая математическая постановка упругого поведения материала включает в себя уравнения равновесия [7]

div с = 0, x eV;

геометрические соотношения s=2 (v и +(V и) T), x eV;

физические соотношения c = X11 (s)I + 2цё, xeV1 иV2,(3)

где X и ц - параметры Ламе; С - тензор напряжений; s - тензор деформаций; u ^r – вектор перемещений; x ^r – вектор узловых неизвестных; I 1 ( s ) - первый инвариант тензора деформаций; I - единичный тензор;

V = V 1 и V₂ и V 3 - область; V 1 - область плиты с шаровым сегментом; V₂ -область плиты со сферическим вырезом.

Для описания поведения материала прослойки выбрана деформационная теория пластичности, физические соотношения которой имеют вид [5]

с = 2Г ( s- 1 ¹ ( s )^ 3 KI ¹ ( s ) I, x e V s , (4) где с _и = ^3 1 ₂ ( C ) - интенсивность тензора напряжений ( 1 ₂ (< с ) - второй инвариант тензора напряжений); s _и = -^^ 1 ₂ ( s ) - интенсивность тензора деформаций ( 1 ₂ ( s ) - второй инвариант тензора деформаций); K - объемный модуль упругости, с _и = Ф( е _и ) - функциональная зависимость, определяемая кривой деформирования; V ₃ – область прослойки.

Математическая постановка включает также кинематические граничные условия на поверхности S ₂ :

и_у = 0 , x e S ₂

и статические граничные условия на поверхности S ₁

σ ˆ ⋅ n ^r = P ^r , x ^r ∈ S ₁ ,                            (6)

остальные наружные поверхности являются свободными:

σ ˆ ⋅ n ^r = 0.                                  (7)

Система уравнений (1)–(7) дополняется граничными условиями на поверхности контакта S_K = S_{K 1} ∪ S_{K 2} ∪ S_{K 3}. Рассматриваются следующие типы контактного взаимодействия:

– проскальзывание с трением: для трения покоя

σ _n < 0, σ _{n α}< q σ _n , u ^{r 1} = u ^{r 2} ,                      (8)

для трения скольжения

12r1r 2 n , nα q n, nn, τ τ , где q – коэффициент трения; un – нормальные к соответствующей контактной границе смещения; индекс α = 1,2 , 1 – 2 условные номера двух контактирующих поверхностей;

– отлипание u1n-un2≥0, σnα=σn=0, α=1,2,                (10)

– полное сцепление ur1-ur2=0, σnα =σn =0, α=1,2.                (11)

Контактная задача упругопластичности в данной работе решена в частном случае осесимметричного напряженно-деформированного состояния.

2.    Идентификация определяющих уравнений

Для изучения поведения материала антифрикционной прослойки проведен ряд натурных экспериментов на одноосное сжатие (эксперименты проведены в ИМСС УрО РАН д.ф.-м.н. А.А. Адамовым). Эксперименты проводились на цилиндрических образцах с диаметром 20 мм, высота равна диаметру (рис. 2).

Материал антифрикционной прослойки – модифицированный фторопласт (фторопласт-4 без наполнителя после облучения). На основе анализа результатов экспериментов в качестве модели поведения материала была выбрана деформационная теория упругопластичности [5]. Проведена серия численных экспериментов с использо-

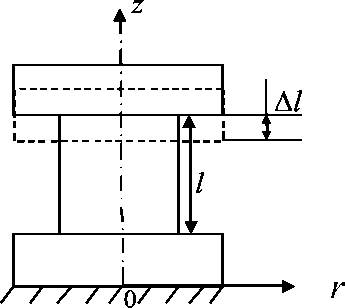
Рис. 2. Схема эксперимента

ванием программного комплекса

ANSYS, направленных на проверку работоспособности выбранной модели поведения материала. В рамках численного эксперимента происходит имитация условий натурного эксперимента с использованием деформационной теории упругопластичности, параметры которой определены из натурного эксперимента. Реализована контактная задача, включающая уравнения (1), (2) и (4), боковые грани свободны, на контактных поверхностях заданы условия контактного взаимодействия с учетом трения (6)–(9), коэффициент трения q=0,04 , нижняя плита пресса неподвижна, к верхней плите прикладывается возрастающее по величине вертикальное перемещение uz =∆l (рис. 2). По результатам численного решения задачи о деформи-

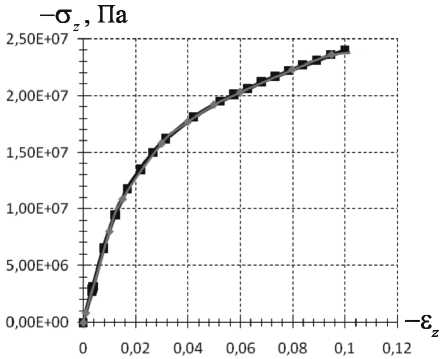
Рис. 3. Диаграммы сжатия σ _z - ε _z

ровании образца определялись поля средних по сечению образца z=l/2 напряжений σz и деформаций εz и строились диаграммы деформирования. На рис. 3 представлены диаграммы деформирования, полученные из натурного эксперимента и численно.

Установлено, что численный расчет с использованием выбранных определяющих соотношений дает хорошее количественное соответствие результатам эксперимента.

3.    Реализация решения и полученные результаты

Реализовано решение осесимметричной контактной задачи, описанной в п. 1. При помощи программного комплекса ANSYS построены конечно-элементные модели с использованием деформационной теории упругопластичности. Используется осесимметричный 8-й узловой элемент, обладающий аппроксимацией 2-го порядка и двумя неизвестными перемещениями в каждом узле. В прослойке произведено сгущение размера элемента, в нижней и верхней плитах размер элементов градиентно увеличивается. Исследовалась сходимость решения от количества элементов по толщине прослойки, рассмотрено четыре варианта: 2 и 4 элемента, 8 и 16 элементов. При уменьшении размера элемента по толщине прослойки уменьшается характерный размер элементов прослойки. На поверхностях соприкосновения верхней и нижней плит с прослойкой нанесена контактная конечно-элементная пара, позволяющая учесть трение.

Изучены особенности напряженно-деформированного состояния конструкции и поведения антифрикционного материала прослойки. На модель наложены статические и кинематические граничные условия, соответствующие реальной максимальной нагрузке при эксплуатации опорной части с шаровым сегментом в пролетных строениях мостов: к верхней плите прикладывается распределенная вертикальная нагрузка: для л-250 P = 54 МПа, для л-350 P = 56 МПа.

В результате решения задачи были найдены зоны контактного взаимодействия, контактные давления и контактные касательные напряжения. Наибольший интерес представляют данные величины на контактной поверхности прослойки, обладающей большей свободой S_{K 1} .

Зоны контактного взаимодействия при разном количестве элементов по толщине прослойки имеют одинаковый вид, но отличаются в конструкциях л-250 и л-350. Зоны контактного взаимодействия представлены на рис. 4.

Разъединение контактных поверхностей не происходит. Проскальзывание наблюдается у края прослойки.

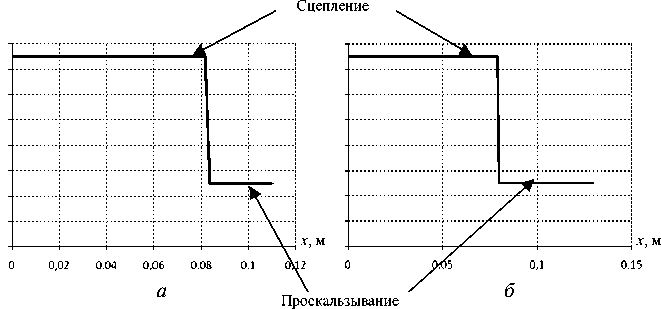
Рис. 4. Зоны контакта S_{K 1} : а – л-250; б – л-350

На поверхностях контакта действуют контактные давления и контактные касательные напряжения. Влияние количества элементов по толщине прослойки на относительное контактное давление P _{K 1} P (отнесено к прикладываемой нагрузке) представлено на рис. 5, отношение контактного костельного напряжения к прикладываемой нагрузке – на рис. 6.

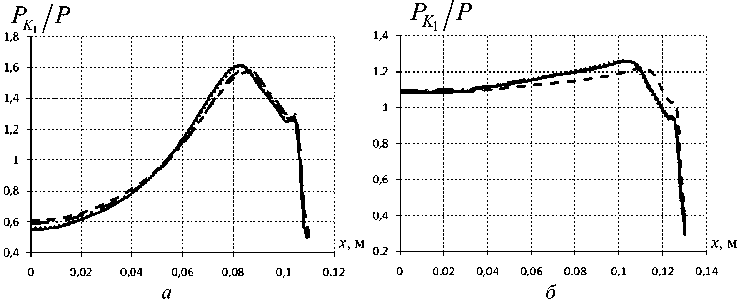
Рис. 5 Относительное контактное давление на S _{K 1} : а – л-250; б – л-350:

8 элементов 16 элементов

2 элемента 4 элемента

Кривые относительного контактного давления для разного количества элементов по толщине прослойки мало отличаются друг от друга и практически сливаются в одну линию. Для опорной части л-250 максимум наблюдается в зоне перехода контактных состояний, у л-350

данная тенденция слабо выражена. У обеих конструкций ближе к краю прослойки заметно снижение контактного давления.

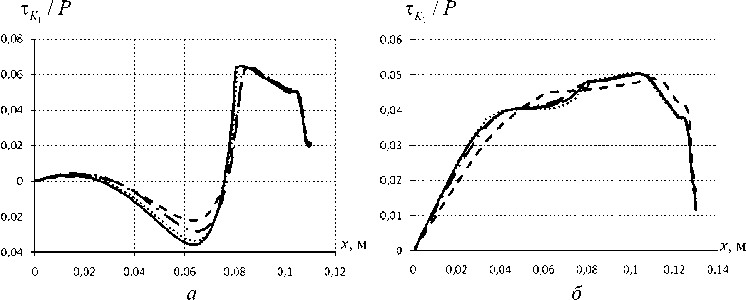
Рис. 6. Относительное контактное касательное напряжение на S_{K 1} : а – л-250; б – л-350;

2 элемента 4 элемента

8 элементов 16 элементов

Значения отношения τ _{K 1} P значительно меньше значений отношения P _{K 1} P . Количественные различия τ _{K 1} P для разных сеток более заметно, но сходимость данной величины менее существенна, так как касательное контактное напряжение дает меньший вклад в полное контактное напряжение. Для опорной части л-250 наблюдается резкое увеличение τ _{K 1} P вблизи зоны перехода контактных состояний, у л-350 данное увеличение τ _{K 1} P мало. Аналогично контактному давлению к краю прослойки заметно снижение контактных касательных напряжений.

Окружное напряжение σ_ϕ мало изменяется в различных сечениях по толщине прослойки, на краю прослойки заметно изменение значений напряжений (рис. 7). Рассмотрим два сечения: центр ( x = 0) и край прослойки ( x ∈ S _{K 3} ) (рис. 8).

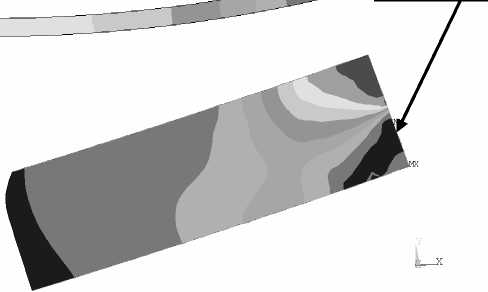
Рис. 7. Напряжение σ _ϕ в прослойке л-250

-6,00 Е+07

2,00 Е+07 -

σ _ϕ , Па

σ _ϕ , Па

-7,ОС Е+07 -г-

-2.7DE+O7

м

б

а

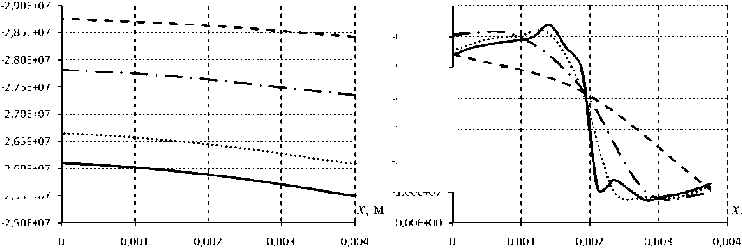
Рис. 8. Напряжение σ _ϕ в прослойке л-250 в сечениях: а – x = 0, б – x ∈ S_{K 3} ;

-5,00 Е+07 - -

-4,00 Е+07 - -

-3.00Е+07 --

-2,Б0Е+07

-2.55Е+07

-1.0СЕ+07 --

2 элемента,     4 элемента

8 элементов 16 элементов

Напряжение σ_ϕ мало меняется в сечении x = 0. У края прослойки заметна неравномерность напряжений (рис. 9). Со сгущением сетки происходит уточнение напряженно-деформированного состояния.

Аналогично конструкции л-250 на основной доле поверхности прослойки конструкции л-350 напряжения σ_ϕ постоянны по сечениям, у края прослойки заметна неравномерность напряжений. Рассмотрим два сечения центр ( x = 0 ) и край прослойки ( x ∈ S _{K 3} ) (рис. 10).

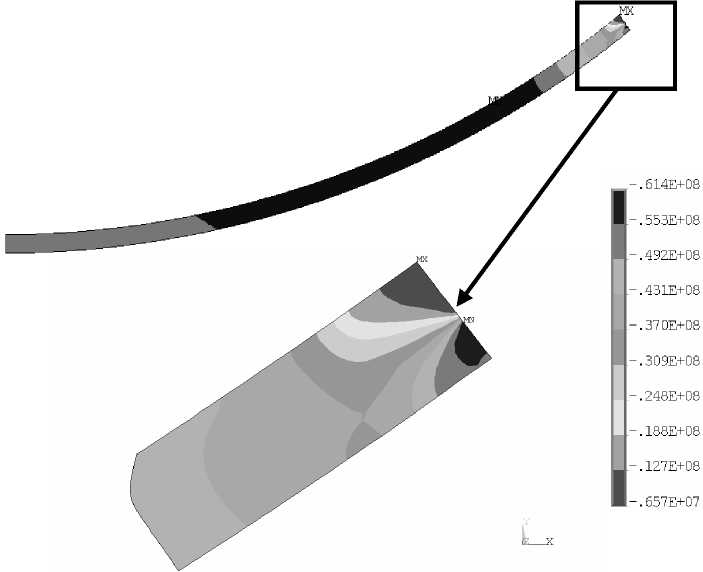
Рис. 9. Напряжение σ _ϕ в прослойке л-350

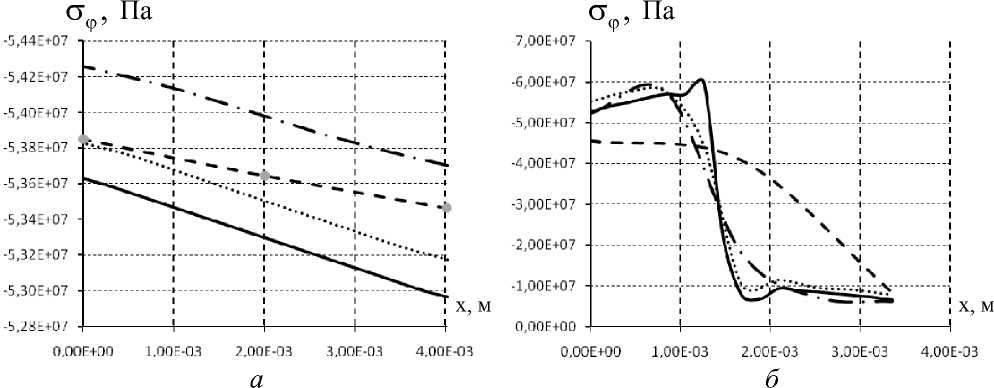
Рис. 10. Напряжение σ _ϕ в прослойке л-350 в сечениях: а – x = 0, б – x ∈ S_{K 3} ;

2 элемента 4 элемента

8 элементов 16 элементов

Таким образом, на основе численного решения осесимметричной контактной задачи упругопластичности изучены картины распределения зон разного типа контактного взаимодействия. Установлены величины и характер распределения контактного давления и контактного касательного напряжения на поверхности контакта, рассмотрено их изменение при увеличении количества элементов при разбиении. Рассмотрен характер распределения напряжений σϕ в прослойке, а также изучено влияние увеличения количества элементов при разбиении на данную величину. Отмечено, что PK1 P и τK1 P уточняются с увеличением количества элементов, PK1 P сходится быстрее, сходимость τK1 P менее существенна ввиду малости величины. На большей доле поверхности прослойки отмечено малое изменение величин напряжений σϕ . У края прослойки колебания напряжений σϕ существенны. С увеличением количества элементов разбиения в прослойке уточняется характер распределения напряжений.