Напряженное состояние в зоне контакта двух цилиндрических тел конечной длины

околоконтактной зоне с приемлемой точностью, обычно применяется теория Герца-Беляева [1, 2] в случае эллиптической площадки. Однако в случае прямоугольной площадки эта теория имеет смысл только для средней части цилиндра конечной длины, так как на краях появляется резкое увеличение контактных давлений обусловленной краевым эффектом. Этот эффект не учитывается в теории Герца-Беляева, где сделано очень серьезное допущение о бесконечности длины обоих кон-тактируемых тел не имеющих краев. Для учета краевых эффектов необходимо привлекать численные методы.

Цель работы: получение и исследование распределения давления и напряженного состояния вблизи краев контактирующих цилиндров с использованием программного модуля Ansys/multiphysics.

Адекватность результатов. Для проверки правильности решения данной задачи результаты, полученные с помощью препроцессора Ansys, сравниваются с результатами математической модели контактной задачи Герца по критериям максимального давления и ширины площадки контакта находящихся в центре длины цилиндра. Математическая модель контактной задачи соответствует частному случаю взаимодействия двух цилиндров.

Описание задачи. Контакт двух цилиндров происходит под воздействием силы F . Радиус кривизны первого цилиндра R 1 =3,75 мм, радиус скруглений по торцам цилиндра R ск =0,5 мм, контактная длина цилиндра l =6,5 мм. Радиус кривизны второго цилиндра R 2 =19,25 мм. Радиальная сила F , действующая на цилиндры, составляет 840,384 Н. Свойства материала цилиндров: модуль упругости E 1,2 =2,1x10¹¹ Па, коэффициент Пуассона v 1,2 =0,33.

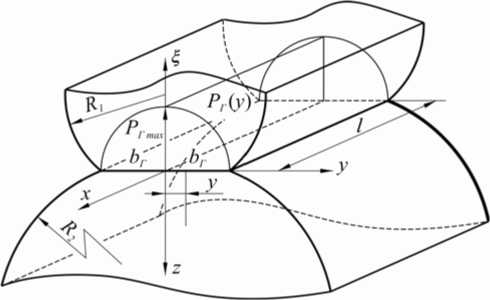
Описание математической модели задачи Герца. При контакте цилиндров под действием распределенной нагрузки по центральной линии в области касания образуется прямоугольная площадка контакта с полушириной b Г (рис. 1), по которой распределяется контактное давление, данная постановка является частным случаем решения задачи Герца. В данной постановке предполагается, что тела обладают бесконечной длиной вдоль оси х .

Максимальное давление в центре площадки контакта

р max =, - ^ q = 1.243Па

пп

Функция распределения давления по площадке контакта

Р_г ( у ) = P, Г         Г max

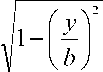
где y =[0, b ] – переменная координата ширины площадки контакта.

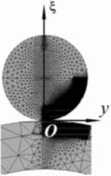
Описание построения моделей в программном пакете Ansys/Multiphysics. На рис. 2 представлены три конечно-элементные модели.

Рис. 1. Взаимодействие двух цилиндров и распределение давления между ними

Порядок расчета: Сначала определим кривизны поверхностей k Σ =1/ R 1 +1/ R 2 =318,615 1/м. Далее находим коэффициент упругих свойств материала η =1 ^ v 1 ²/ E 1 +1 ^ v 2 ²/ E 2 = 84,866x10^{^11} м²/Н. Вычисляем нагрузку, действующая на единицу длины цилиндра q = Q / l =129289,941 Н/м. Полуширина площадки контакта b _Г = д/ 4 n q (лк _х = 6,621 ^х 10 5 м.

а

б

в

Рис. 2. Исследуемые модели и их расположение систем координат: а – первая постановка, б – вторая постановка, в – третья постановка

Таблица 1. Граничные условия для первой, второй и третьей постановок

			Первая постановка (рис. 2, а)	Вторая постановка (рис. 2, б)	Третья постановка (рис. 2, в)
тип эле мента	Модель		PLANE182	SOLID45
	контактные по-верхно-сти	целевая (нижний цилиндр)	TARGET169	TARGET170
		контакт ная (верхний цилиндр)	CONTA172	CONTA174
ГУ	нагрузка	значение	q	Q /14	Q /16
		приложение	к центру верхнего цилиндра	к каждому узлу центральной линии верхнего цилиндра, 14 узлов	к каждому узлу центральной линии верхнего цилиндра, 16 узлов
		направление	в сторону целевой поверхности перпендикулярно касательной к этой поверхности
	закрепления		внутренняя поверхность нижнего цилиндра

Первые две постановки соответствуют решению классической задачи Герца в плоскости (рис. 2, а) и объеме (рис. 2, б). Во второй постановке предполагается, что тела имеют бесконечную длину вдоль оси х . Третья постановка (рис. 2, в) создавалась на основе двух вышеперечисленных, длина тел ограничена и края верхнего цилиндра имеют форму скруглений с радиусом R ск . На рис. 2, в плоскость z 1 Oy 1 совпадает с точкой касания края верхнего цилиндра с поверхностью нижнего, плоскость zOy делит модель по длине на две равные части, оси ξ и ξ 1 – вспомогательные. Использована не вся поверхность нижнего цилиндра, а только его часть, находящаяся непосредственно в месте расположения верхнего. В околоконтактной зоне уменьшена сетка конечных элементов. Типы элементов и граничные условия (ГУ) для каждой задачи отражены в таблице 1.

Адекватность построенных моделей в программном пакете Ansys/Multiphysics с математической моделью задачи Герца. Проверка проводилась по критерию контактного давления, создаваемого в контактной паре. На рис. 3 представлены графики распределения давления по площадке контакта в плоскости ξOy .

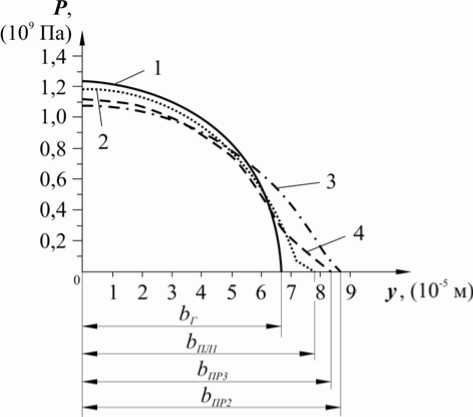
Рис. 3. Распределение давления в плоскости ξOy : линия 1 – по Герцу Р Г (y), линия 2 – в первой постановке задачи P ПЛ 1 ( y ), линия 3 – во второй постановке задачи P ПР 2 ( y ), линия 4 – в третьей постановке задачи P ПР 3 ( y )

Каждая линия графика соответствует распределению давления по площадке контакта для каждой из поставленных задач. Линия 1 соответствует аналитическому решению задачи Герца, в которой давление распределяется по закону (2), где значение максимального давления определено формулой (1). Линии 2, 3, 4 соответствуют распределению давления в первой (рис. 2, а), второй (рис. 2, б) и третьей (рис. 2, в) постановках, соответственно. Максимальные давления и полуширины площадок контакта для первой, второй и третьей постановок принимают значения: РПЛ1max=1,185x109 Па, bПЛ1=7,8х10^5 м, РПР2max=1,077x109 Па, bПР2=8,4х10^5 м; РПР3max=1,121x109 Па, bПР3=8,4х10^5 м, соответственно. Наблюдается излом линий 2, 3, 4 близ оси ординат в сторону возрастания полуширины площадки контакта. Это вызвано тем, что конечная точка графиков совпадает с узлом конечно-элементной модели. Поэтому можно сказать, что значение величины площадки контакта чуть больше значения y точки излома кривых. Для получения более точного решения можно разбить модель на еще большее число конечных элементов, но расхождения не велики, и конечный результат можно считать удовлетворительным. Сравнение величин максимальных давлений первой, второй и третьей постановок с величиной максимального давления в решении задачи Герца дало следующие результаты: PПЛ1max/PГmax = 0,953; PПР2max/PГmax = 0,866; PПР3max/PГmax = 0,902.

Влияние краевого эффекта. Распределение давлений. Очень серьезной и вместе с тем малоизученной особенностью линейного контакта является краевой эффект, которым принято называть повышение давления у концов двух соприкасающихся цилиндров. На рис. 4 представлена 1/4 часть площадки контакта, в третьей постановке задачи.

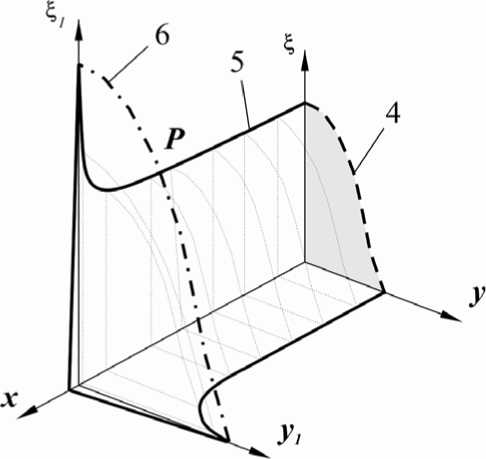
Рис. 4. Распределение давления по 1/4 части площадки контакта

Представим числовые значения на рис. 5. Рис. 5 является разверткой рис. 4. b L =3,3x10^{^5} м – полудлина площадки контакта, b K =1x10^{^4} м – полуширина площадки контакта на краю цилиндра, P K max – максимальное значение давления на краю цилиндра, P L max – максимальное значение давления по цилиндра. Расположение плоскостей ξOx , ξOy и ξ 1 Oy 1 можно увидеть на рис. 2 в.

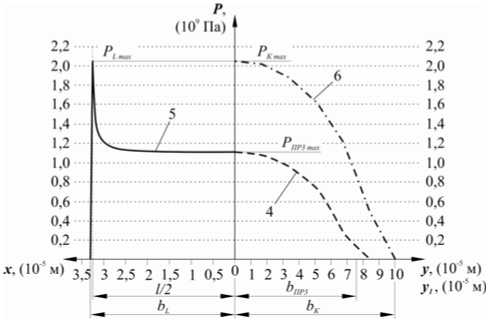
Рис. 5. Распределение давления на площадке контакта по осям x , y , y 1 . Линия 5 P L ( x ) находится в плоскости ξOx , где давление распределено по длине цилиндра; линия 4 представлена на рис. 3; линия 6 P_K ( y ₁) в плоскости ξ ₁ Oy ₁, давление распределенное по краю цилиндра

График (рис. 5, линия 5) имеет постоянное значение на большей части длины цилиндра, однако при приближении к краю имеет место резкий скачек давления: P K max = P L max = 2,054x10⁹ Па. Точка пика совпадает с точкой края цилиндра, значение ее на оси x соответствует l /2=3,25. Такое распределение выходит за рамки теории Герца, пик давления на краях примерно в 1,8 раза превышает распределение давления в плоскости, проходящей через центр цилиндра: P K max / P ПР 3max =1,832.

Постановки задач на рис. 2 а и рис. 2 б, как уже говорилось, соответствовали решению Герца. В первой постановке распределение давления находится в плоскости ξOx (рис. 6, а).

Во второй постановке сделано предположение о бесконечной длине контактируемых тел, и давление распределяется равномерно (рис. 6, б ). В третьей постановке (рис 2, в ) контактные давления достаточно точно рассчитываются по теории Герца вдоль большей части длины цилиндра, однако вблизи торцов (рис. 6, в ) наблюдается резкое увеличение давление, распределение которого принимает вид "собачьей кости" [7].

Рис. 6. Распределение давления на площадке контакта в разных постановках задачи: а – первая постановка, б – вторая постановка, в – третья постановка

Напряженное состояние . Рассмотрим распределение напряжений внутри цилиндра (рис. 7), выраженных в безразмерных координатах. σ ПР 3 Х , σ ПР 3 Y , σ ПР 3 Z , σ ПР 3 Э – компоненты напряжения x , y , z и эквивалентное напряжение, действующие вглубь от центра цилиндра. σ KX , σ KY , σ KZ , σ KЭ – компоненты напряжения x , y , z и эквивалентное напряжение действующие вглубь нижнего цилиндра от точки касания края верхнего цилиндра.

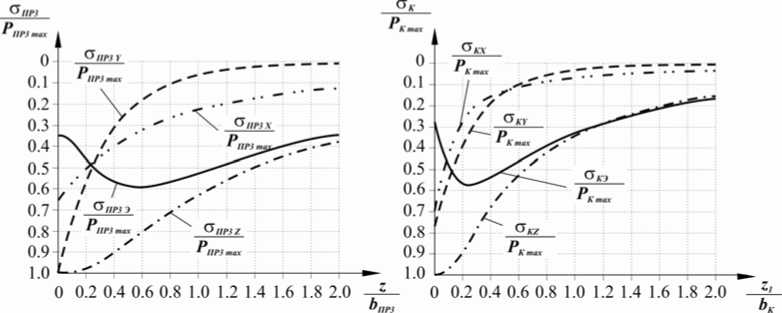
Рис. 7. Распределение напряжений внутри цилиндра в третьей постановке задачи: слева – по оси z, справа – по оси z 1

Графики распределения напряжений на рис. 7 (слева) подтверждают правильность решения задачи Герца-Беляева о распределении напряжений вдоль полосы контакта [2, 3, 7], однако наблюдается интересный эффект у края цилиндра (рис. 7, справа): напряжения σ KY / P K max и σ KX / P K max имеют практически одинаковые значения по всей глубине. Кривая эквивалентных напряжений σ KY / P K max имеет более крутой изгиб на крае нежели в центре σ ПР 3 Э / Р ПР 3max . Концентрация эквивалентных напряжений вдоль большей части длины находится на глубине 0,6, на краю это значение падает до 0,3. На рис. 8 представлены изолинии напряжений для третьей постановки задачи, где также можно заметить увеличение эквивалентных напряжений на краю цилиндра.

Рис. 8. Распределение эквивалентных напряжений в нижнем и верхнем цилиндрах в третьей постановке задачи

Выводы:

- Предложена методика расчета позволяющая анализировать задачи контакта цилиндр-цилиндр с разной геометрией краев тел с помощью конечно элементного алгоритма в программном пакете Ansys.

- Данное исследование позволило получить распределение давлений и характеристики напряженного состояния, когда края цилиндра имеют форму скруглений у торцов.

- Кривые напряженного состояния, не соответствующие классическому решению задачи, следует проанализировать на нескольких примерах с разными геометриями краев тел в программном комплексе Ansys для выявления закономерностей краевого эффекта.

- Методика расчета применима для решения задач контактирования зубьев зубчатых колес, ролика и кольца подшипника качения, колеса и рельса, подшипника скольжения и коленчатого вала двигателя внутреннего сгорания и других задач со схемой взаимодействия цилиндр-цилиндр.