Напряжённо-дефомированное состояние упругого слоя при локальном нагружении

Расчётное или экспериментальное определение напряжённо-деформированного состояния (НДС) является центральной частью любой задачи о прочности конструкций ракетно-космической техники. Значительная часть задач расчёта НДС приводит к решению краевой задачи с необходимостью аналитического или численного интегрирования системы сингулярных дифференциальных уравнений в частных производных в окрестности особой точки. Высокоградиентный характер изменения функций, полученных в качестве решения и описывающих напряжённое состояние с высоким показателем изменяемости, требует, как правило, не только определения величины напряжений, но и точного их позиционирования относительно зон конструкций, требующих повышенного внимания. Знание точных координат действующих напряжений необходимо, например, для зон сварного шва, термического разупрочнения, места расположения выявленного дефекта конструкции или структуры материала и т. п. Примеры специфического подхода к решению задач прочности для подобных зон оболочечных конструкций изложены в работах [1–3].

Развитие вычислительной техники, повышение её возможностей, разработка соответствующих программных продуктов привели к почти полному вытеснению аналитических методов численными, а из численных — практически стопроцентному использованию метода конечных элементов. Однако получение с их помощью корректного результата в окрестности особой точки связано с некоторыми сложностями. Значительное число работ, посвящённых исследованию локального нагружения, построено на теории пластин и оболочек.

Однако, как известно, теория, построенная на гипотезе неизменяемости нормального элемента (гипотезе Кирхгофа–Лява), вносит в результаты погрешность порядка h / R , за исключением особых случаев, характерным примером которых является НДС с высоким показателем изменяемости.

В данной статье рассмотрена задача о действии сосредоточенной силы на упругий слой. Причём отличительной особенностью подхода является то обстоятельство, что задача определения НДС в окрестности точки действия силы рассматривается в трёхмерной постановке. Полученное решение использовано как функция влияния (функция Грина) в задаче о произвольной нагрузке, распределённой по произвольной области.

однородные уравнения равновесия

При отсутствии поверхностных и массовых сил уравнения равновесия в перемещениях и граничные условия для упругого слоя, ограниченного плоскостями z = ± 2 , в цилиндрической системе координат записываются следую- щим образом [4]:

grad div ^→ u + (1 – 2ν) ∇ ^{2 →} u = 0

– ^h <  z <  ^h , 2

∂u∂

+= 0,

∂z∂

∂v1

+   .= 0,

∂ zr

h z = ± 2,

v div и - ( 1

∂ w

2 v)

∂z где u, v, w — проекции вектора пере-→ мещения u на координатные оси;

div → u	∂ u = —--+ д r	1 <    д у — 1 и + — r ^ дф	∂ w — + —— ’
∇ 2 =	д2     1 + д г2   г	∂1 .        +      . ∂ r    r 2	д2     д2 дф2 д г 2

Классическое решение А. Лява, соответствующее прогибу пластины (функция w — чётная, а u и v — нечётные):

u =

2 – ν

_{3 ν}

∂θ0

z ³     – z

∂ r

h ² ∂θ₀ ∂θ₁

.         +          ;

2ν ∂ r ∂ r

2 – ν   1  ∂θ       h2  1  ∂θ    1

z3    .     0 – z . .     0 +     .1

3ν    r  ∂r      2ν  r  ∂ϕ    r∂ϕ

w = z ²θ₀ + θ₁,

где θ₀ и θ₁ — гармоническая и бигармони-ческая функции переменных r и ϕ, соответственно, удовлетворяющие соотношению

∇ ²θ₁ =

2(1 – ν ) ν

θ 0 .

Вторая группа функций, являющихся решением краевой задачи (1), ищется в форме, предложенной И.М. Рапопортом [5]:

∂Φ u = (1 – 2ν)f(z)    ,

1 ∂Φ v = (1 – 2ν)f (z) .     , r ∂ϕ

;

w =

∂ q 2(1 – 2ν)    –

_{∂ z}

^{∂ f}

∂ z

Φ

λz λz    λz     λz λz    λz f = c1 h  cos h + c2 h  + c3 h sin h + c4 h ,

λ z    λ z               λ z

g = c ₁

h cos h – 2(1 – 2 ν )sin h

λ z

+ c ₂ sin h + c ₃

Граничные условия (6) дают систему однородных алгебраических уравнений

λλ     λ

c ₁

2 cos 2 – 2(1 – ν) sin 2

λλ λ c1 (1 – 2ν) cos 2 + 2 sin 2

λλ

λ

λ

+ c ₂sin ₂ = 0,

λ

– c ₂cos ₂ = 0,

λ

c sin + 2(1 – ν) cos    – c cos

3   _{2      2                  2}       4     ₂

= 0,

λλ λ c (1 – 2ν) sin   – cos

3                _{2    2      2}

λ

+ c ₄sin ₂ = 0.

1 ∂Ψ u = χ(z) .     , r ∂ϕ

∂Ψ ^, v = ^- x( z )^ ,

w = 0

где Φ и Ψ — функции r и ϕ, являющиеся решением уравнений

λ2

∇2Φ –   Φ = 0, h2

,

µ2

∇ ²Ψ –  Ψ = 0

h ²

Подставляя перемещения (2) в уравнение и граничные условия (1) и учитывая систему (4), получим для функций f ( z ) и g ( z ) систему дифференциальных уравнений

d ² f d ² g λ²

2ν d z ₂ – d z ₂ = h ₂ (1–2ν) f ,

^df –2(1– ν ) ^{d g} = ^λ (1–2ν) g dz ²             dz ² h ²

с граничными условиями

ν f – (1 – ν) g = 0,

h df          dg z = ±   .(6)

ν    – (1 – ν)    = 0

dzdz

Общее решение системы (5)

λ z    λ z               λ z

h sin h + 2(1 – 2 ν )cos h

λ z

+ c ₄ cos h

Ненулевые решения этой системы имеют место при равенстве нулю её определителя. Из чего следуют два трансцендентных уравнения для вычисления параметра λ:

λ + sinλ = 0;

(9) λ – sinλ = 0.

Для двух пар собственных функций f ( z ), g ( z ) и f ′( z ), g ′( z ), соответствующих собственным значениям λ и λ′, согласно системам (5), (6) будет иметь место равенство:

h /2

(X² - X‘²)(1 - 2v) J (ff‘ - gg ‘) dz =

-h /2

,2- df  d2gL L dg 1. L df  dgLdf d^ 1L h I | 2v dz2    dz2 )f  [ dz2   2(1 v) dz2 Jg  [2v dz*    dz* f  [ dz2   2(1 v) dz2 Jg I dz

-h /2

df

= h² z < 1 2v----- dz

^{d g} f ′ dz

dL - 2(1 - v) dg dz           dz

g' -

f2v ^L - dA f + к dz dz )

L - 2(1 - v) ^ dz           dz

z = h /2

= 0,

z = - h /2

из которого следует условие биортогональности собственных функций, соответствующих различным собственным значениям:

Вычисляя интегралы с учётом соотношений (9), получим значения постоянных:

c (1) =

h /2

при λ ≠ λ′ ∫ ( ff ′ – gg ′) dz = 0.      (10)

-h /2

Для определения постоянных из системы (8) условие ортогональности (10)

дополним условием нормирования:

1/2

J [ f⁽ k ⁾²(^) — g ( k ⁾² (^)l d^ = 1

- 1/2

( k = 1, 2; j = 1, 2, 3, …).            (11)

c (2) =

2(1 – 2 ν ) cos ^λ 2

2(1 – 2 ν ) sin ^λ 2

Таким образом, собственные функции краевой задачи (5), (6), соответствующие собственным значениям λ^{( k )}, удовлетворяющие условиям ортогональности (10) и нормирования (11), можно записать в следующем виде:

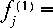
_λ (1)

2(1 – 2 ν ) cos 2 ^j

X <^z     X

(1)                     1

g_{j                          λ (1)}

2(1 – 2ν) cos 2^j

f_{j                            λ (2)}

2(1 – 2ν) sin 2^j

_gj(2)

_{λ (2)} 2(1 – 2ν) sin 2^j

_λ(1)z ^j

h

_λ(2)z j

h

_λ(2)z ^j

h

_λj(1)z sin + sin h

_λ(1)

²2 ^j– 2ν cos

_λj(2)z cos + sin _h

_λ(2) 2j

cos

_λ(2)z ^j

h

cos²

_λ(2) ^j

_λ(1)z ^j

h

+ 1 – 2ν sin

,

_λ(2)z ^j

h

_λ(2)z

2ν sin ^j h

,

.

Подставляя перемещения (3) в уравнение (1) и учитывая уравнение (4), получим для функции χ дифференциальное уравнение

с граничными условиями

^dχ= 0 dz

z =

h

± 2 '

d²χ dz²

+ h^µ2²χ = 0

hh

2 < z< 2

Для собственных функций χ имеет

место равенство

I z = h /2

d²X      d²X k )

X. Idz = h²z —jx,--x ^             dz²k^k    dz^{2 k}i z=-^h/²

h/2           h /V d2X.     d x n2(k2 - j2) I xx,dz = h2 [ I -—j-xk--ryk j k               dz2 k dz2

-h/2              -h/2

из которого следует условие ортого-

нальности:

h/2

при j ≠ k

∫ χ_jχ_kdz = 0. –h/2

^χj

z

2 cos π j h

z

2 sin π j _h

j = 2, 4, 6, ...

j = 1, 3, 5, ...

С учетом условия нормирования

1/2

∫ χ²_j dξ = 1,

j = 1, 2, 3,…

–1/2

собственные функции краевой задачи получат следующее выражение:

Таким образом, общее решение однородных уравнений равновесия с однородными граничными условиями (1) в виде линейной комбинации полученных выше функций запишется в следующем виде:

∂ϑ₁ u = ξ –

∂r

∂ϑ      h²∂θ ∂θ ∂θ 1 ∂ϑ 2 – ν ∂ϑ

² – z^{. 0} +     ¹ +     ² + z^{2 .    0} + z^{3         .    0}

∂r      2ν ∂r    ∂r     ∂r       2 ∂r       3ν   ∂r

∞ 2                 ∂Φ_j         1 ∂Ψ_j

+ Σ Σ (1 – 2ν) f^(k) (z)     + χ^(k)(z) ^.

j = 1 k = 1             ^j       ∂r       ^j r ∂ϕ

v = η– r

∂ϑ1

∂ϕ

r

∂ϑ 2 ∂ϕ

h2  1  ∂θ0    1   ∂θ11

. .        +    .+

2  r  ∂ϕ   r  ∂ϕ

∂θ      1 ∂ϑ

² + z^{2 .    0} +

∂ϕ      r ∂ϕ

∂ϕ

2 – ν

+ z  _3ν

1 ∂ϑ∞

. 0 + Σ r ∂ϕ j = 1

2                 1 ∂Φ

Σ (1 – 2ν) f^(k)(z) ^{. j} k = 1            ^j r ∂ϕ

1 ∂Ψ χ(j k ) (z) ₂ . _∂r ^j

w = ®i ⁺^₂

^  2

- zO_o+ S S 2(1 - v)

⁰j = 1 k = 1

dg(^k) dz

df^^k)" dz

^Φj^,

где ϑ2 и θ2 — гармонические функции, выделенные из бигармонических ϑ1 и θ1.

неоднородные уравнения

→

При действии системы массовых Q →→ и поверхностных сил q+ и q– уравнения равновесия с граничными условиями приобретают вид

G (1 2v grad div^ + V²m j + (Q = 0

P→ = Q→ + δ z – 2h q→+ + δ z + 2h q→–, получим неоднородное векторное уравнение с однородными граничными условиями, которые запишем в перемещениях

G f i _ 2_V graddivM + V²m j + P⁵= 0

h

–₂< z<

h

2;

h

h

–₂< z< ₂;

τ = q⁺, τ = q⁺, σ = q⁺ rz r     ϕz      ϕ z z

h z 2;

τ_rz = q_r, τ_ϕz = q_ϕ, σ_z = q_z

h z = –

∂u∂

+= 0,

∂z∂

∂v 1 ∂w

∂z⁺r^. ∂ϕ

z = ± ₂ .    (15)

.

Введя через δ-функцию эквивалентные массовые силы

∂w v div u + (1 – 2ν)    = 0

_∂z

2G(1 – ν) 1 – 2ν

1 – 2ν         h2                z2          2 – ν ∇2ϑ +          ϑ – z    ∇2θ – z∇2θ +   ∇2ϑ + z3     ∇2θ + 2                   3     2ν      0         2   2      0        3ν      0

∞2

_λ(k)

Введем трёхмерные функции нагрузки R(r, ϕ, z), Φ(r, ϕ, z), Z(r, ϕ, z), определив их с помощью следующих уравнений:

Подставляя перемещения (14) и учитывая, что

grad div^→u^→e_r

∂R	1	∂Φ
∂r	+ . r	∂ϕ
1	∂ R	∂Φ
. r	∂ϕ –	∂r
∂z
dz	= P. z

P =, ^ϕ

P r,=

= _∂^∂r (div^→u);

.

В проекциях на оси цилиндрической системы координат уравнение равновесия записывается следующим образом

1        →→→

G grad divu + ∇²u e + P = 0;

1 – 2ν

1        →→→

G grad divu + ∇²u e + P = 0;

1 – 2ν

1        →→→

G grad divu + ∇²u e + P = 0,

1 – 2ν

→→→ где er, eϕ, ez — единичные векторы осей координат.

grad div^→u^→e_ϕ

grad div^→u^→e

^{1. ∂}(div^→u); r ∂ϕ

∂→

=    (divu);

∂z

а также, что

∇²e = – e ;        ∇²e = – e ;

r r r                   ϕ        r2 ϕ

∂e→             ∂e→ r =→           ϕ =   →

∂ϕ     ^ϕ ∂ϕ ^{r ,}

из чего следует, что

∇2 →u→e =		1	2	∂v
	∇2u –	u –		.;
r		r 2	r2	∂ϕ
∇2 →u→e =		1	2	∂u
	∇2v –	v +		.
ϕ		r2	r 2	∂ϕ

∇^{2 →}u^→e = ∇²w, z

получим

+ Σ Σ (1 – 2ν) f^(k)(z) j = 1k = 1                   ^j

+ R = 0,

∇²Φ^(k) –   ^j   Φ^(k)

j h2 j

G

∞                  π²j²

ψ + Σ χ (z) ∇²Ψ – ψ²

¹j = 1 ^{j              j}       h^{2     j}

+ Φ = 0,

.       (17)

ν          1 – 2ν            h²             ν                ν

2G (1 – ν)        ∇ϑ +         ϑ – z           ∇²θ +        ∇²ϑ + z²         ∇²ϑ +

1 – ν 2   (1 – ν)2 3     4ν(1 – ν)    0 1 – ν 2      2(1 – ν) 0

1 + ν ∞ 2                             λ^(k)

+ z³       ∇²θ + Σ Σ (1 – 2ν) g^(k)∇²Φ^(k) – ^j Φ^(k)+ Z = 0

3ν ⁰j = 1k = 1                ^{j j} h^{2 j}

Из граничных условий получаем

₃ = ¹~^v

³    4 G

h

h

R, Ф,--

.’          2,

Z I r, ф, — I+z . 1’ 2 J

V²O_o=

3v Г ( hA "№ ^z Г’^ф- d

–Z

h

R, Ф,--

’          2,

3     h/2

—J P_z(^R’ ф, z)dz.

Gh^{3 z}

-h/2

С учётом ортогональности и нормирования собственных функций из первого и третьего уравнений системы (16) получим

^T ^v28- ^{+ л}- ⁺^у ®3 = а I К¹ - v)R - VZ] dz;

Х ’-h h2(89r3v) v2e0 + v2e2 = -G - [(1 - V)R - VZ]zdz;

2 Gv⁰²

-h2

^(1)2                                    1

V²Ф⁽¹- - j- Ф^{( 1}- + b⁽⁽¹⁾ V²0- = - —----—   (f⁽¹⁾R - g<‘Z)dz;

j     h2   11    0     2(1 - v)G J/2 11

^(2)2                                1

V²Ф⁽²⁾ j

-А— Ф²) + b(²⁾V²0_n =--[ (f⁽²⁾R - g⁽²⁾Z)dz,

где b(1) =------------------- f [(1 - v)f⁽¹⁾- vg⁽¹⁾] z²dz;

1     2(1 - v)(1 - 2v)            ,J 1J

₁              hf2

b<²> = 121^^(1^20 I {2(1 — v)[2(2 - v)z² - 3h²] f_j<²> - [4(1 - v²)z² - 3h²]g<²>}zdz.

Из второго уравнения системы (17) получим

1 H/2

y, - ^-gh J ^фdz;

-h/2

_П2 j 2                 h /2

• V²^ - -rjr ^  --f Фх dz-

• j h²j G^Jj

  -h/2

действие сосредоточенной силы

Будем считать, что в области r < ρ действуют эквивалентные массовые силы

P = P = –¹ δ(z – ^h). z     πρ2        ₂

Функции нагрузки, определяемые уравнениями (16), при r > ρ равны нулю, а при r < ρ

R = Φ = 0; Z = ∫ P_z(x)dx.

–h/2

Учитывая свойства δ-функции, а также формулу Дирихле для интегралов, зависящих от параметра, получим для r < ρ z

P dz = –    ,

–h/2 ^z         πρ²

h/2           h/2   z                          z

J Zdz = J J Pz(x)dxdz = [z J Pz(x)dx|^;//₂--h/2        -h/2 -h/2                   -h/2

h/2                     h/2               h/2

- J zPz (z) dz = у J P_z (z) dz - J zPz (z) dz

-h/2

-h/2             -h/2

По той же схеме получаем равенство нулю следующих выражений:

h/2                    h/2

J zZdz - 0; J j)Zdz = 0.

-h/2                 -h/2

В результате уравнения для определения функций в формулах (14) приобретают вид для r < ρ:

1 — v

$3 = ^- 4nGP2;     $0 = $3 ⁺ ®;

1 + ν

∇²ω = 0;            ∇²ϑ₁ =_ν ϑ₀;

H²

14- v4 ⁺ v²2 ⁺

1 - 2 v v(1 - v)

93 = 0;

d^    12

+   ^ = dr    rv

_λ(1)2

∇2Φ( 1 ) – j j        h2

фi) = — bjv>у290  (■ = 1,

V²^, = —

л ²i²

-j ^ = 0  (j = 2, 4, 6,...);

∇²θ0 = –

3ν

^;∇²θ = ^{2(1 ν)}θ;

Gh³πρ^{2        1} ν ⁰

∇²θ₂ = –

h 2(8 – 3 ν)_∇2_θ;

λ(2)2

∇²Φ^{( 2 )} – ^j Φ ^{( 2 )}=          b⁽²⁾ при r< ρ, (18)

^j h^{2 j}      Gh³πρ^{2 j}

_λ(2)2

у2ф(2) —      ф(2 > = 0 при r > p.(19)

Решение уравнения (18), имеющее конечное значение при r = 0, λ(2)

(2)                 j(2)

Φ_j     c_j I_{0 h} r     _{G h π ρ 2 λ j( 2 ) 2}b_j ,

У²Ф(²>-j

X(²)²

L ф(²) = _ b^у²O_o(j= 1, 2, 3,...);

решение уравнения (19), стремящееся к нулю на бесконечности,

V ^ = - hr ^ = 0  (j = 1, 3, 5,...);

для r > ρ

1 + v ∇²ϑ0 = 0;               ∇²ϑ1 = _ν ϑ0;

d^ 1     2          д (д'    1 A

+ v 2 =   ^o;              + ^т 21 = о д r    2 v 0      д r Vdr    2

_λ(1)2

∇²Φ^{( 1 )} – ^j   Φ ^{( 1 )} = 0 ;

j        h2      j

∇²Ψ = – ^{π j} Ψ = 0 j         _h2     j

2(1 – ν)

∇²θ₀ = 0;   ∇²θ₁ = _ν    θ₀;;   ∇²θ₂ = 0;

_λ(2)2

∇²Φ^{( 2 )} –   ^j   Φ ^{( 2 )}= 0 (j = 1, 2, 3, ...);

j        h2      j

∇²Ψ = – ^{π j} Ψ = 0 (j = 1, 3, 5, ...).

j         _h2     j

Решив уравнения, выполнив при r = ρ

сопряжения функций ξ, ϑ0, ϑ1, ϑ2, ∂

∂ϑ₀ ∂r^,

(ϑ + ϑ ) и переходя к пределу при ρ → 0,

_∂r     1     2

получим выражения для искомых функций:

3ν

θ₀= – _{G h 3 πρ 2}lnr + c₁;

θ1

3 ( 1 – ν)

_{4 π G h 3}

r² ( l n r

1 – ν

-

2ν

r²c₁;

θ2 =

3(8 – 3 ν ) 40πGh

lnr + c₂.

Для функций Φ_j и Ψ_j получаем

Φ⁽_j¹⁾ = 0; Ψ_j = 0 (j = 1, 2, 3, …);

Φ(2) = c′K j j 0

_λ(2) j_r

h

где I₀ и K₀ – модифицированные функции Бесселя первого и второго рода нулевого порядка.

Условия непрерывности функций Φ⁽_j²⁾ и их производных при r = ρ дают алгебраическую систему для определения произвольных постоянных

λ(2)             λ(2)               3ν j                           j                                         (2)

c_j K₀h ρ + c_j I₀h ρ      G h_{π ρ 2 λ j( 2 ) 2}b_j ,

_λj(2)                _λj(2)

-c'K.      p + c"I. -4— p I = 0.

j 1 h           j 1 h

Учитывая свойство определителя

Вронского для функций Бесселя

I_n(x)

d K _n(x) d x

– Kn(x)

^{d I n ( x )} dx

x ,

определяем значение постоянной

c^j    b^j Ghπρλ_j⁽²⁾I¹

Переходя к пределу

1 lim I ρ→ 0 ρ 1

_λj(2) _h^ρ

_λ(2) j

2h

получим c_j′ = –b_j⁽²⁾

3ν 2πGh^3.

_λ(2) j

h ρ

Формулу для вычисления коэффициентов b_j⁽²⁾ можно представить в следующем виде:

b(2) = ----------------------- x j 12(1 - v)(1 - 2v)

x {2(1 - v)[2(2 - v)Ji - 3h²J2] - 4(1 - v)Jз - 3H/4},

h/2

h/2

где J₁ = ∫ f⁽_j²⁾(z)z³dz;    J₂ = ∫ f⁽_j²⁾(z)zdz;

-h/2

h/2

J₃ = ∫ g⁽_j²⁾(z)z³dz;

-h/2

J₄

Подставляя в интегралы ций (12) и учитывая получим после ряда значения коэффициентов

-h/2

h/2

= ∫ g⁽_j²⁾(z)zdz.

-h/2

значения функ-уравнения (9), преобразований

b(2) = j

h⁴

6v ^2(1 - 2v)

_λj(2) sin²₂^j

и решение уравнений (18), (19)

Φ⁽²⁾ = – j

h

4 πG 2(1 – 2ν) sin^{2 λ}2^j(2)

в

Подстановкой формулы (14)

найденных получаются

для перемещений

_λ(2) j

j

K₀     r

h

.

функций выражения

3(1 – ν)

w = –          r²lnr +

4πGh³

1 – ν c r2 + c

2ν 1      2

zc –

3(8 – 3ν)

_{40 π}G h lnr + z²

3ν

3ν

∞

Σ

4πG 2(1 – 2ν) ^{j = 1}

2(1 – ν)

_dgi(2)    _dfi(2)

d z

d z

_{λ j(2)} sin²₂

c₁

λ j r,

0 _h

1 – 2ν 1    1 – ν 3(1 – ν)          1     9(6 – ν)

^.    + cr + z           r lnr +     +

8πGν  r 2 ν         2πGh³          2     40πGh

2 – ν 1

– z^{3          .} +

2πGh³r

1 – 2ν

∞

Σ

4πGh 2(1 – 2ν) ^{j = 1}_sin

_λj(2)

_λ(2) 2  ₂j

λ

K ^j r f⁽²⁾.

1 h i

lnr –

2πGh³       2πGh³

1    1 – ν

r

2ν

cr

Напряжения, соответствующие этим перемещениям, определённые по известным

формулам теории упругости:

σ r

² πh

1 – 2ν 1    1 + ν h +     πGhc + z

8ν      r² ν

2 – ν 1

3                .

+ z  _{2h2   r2} +

1∞

4h 2(1 – 2ν) ^{j = 1}

_λ(2) ^j

_λj(2) sin²  ₂

^{3 ( 1 + ν )} lnr + ^{3(3 + ν )}

9(6 – ν) 1

₄₀    . _{r 2}

1 + ν ν

πGhc₁ +

K₀^{λ j} r [νg_i⁽²⁾ – (1 – ν)f_i⁽²⁾] – h

h

_{λ (2) r} K₁ j

_λ(2)

j r h

(1 – 2ν)f_i⁽²⁾

2   1 – 2ν   1    1 + ν           3(1 + ν)        3(1 + 3ν) 9(6 – ν) 1

σ =            h + πGhc + z          lnr +          –          ^.

^ϕ   πh    8ν      r²      ν                 2h²              4h²          40      r²

1 + ν ν

πGhc₁

2 – ν 1             1         ∞ λ⁽²⁾

.    _{+                  Σ}j

²h r     4h 2(1 – 2ν) ^{j = 1      λ}j⁽²⁾

sin2

_λ(2)                         _{h         λ}(2)

K ^j r ν(g⁽²⁾ – f⁽²⁾) + K ^j r 0 h i i        _λj(2)r    1 h

(1 – 2ν)f_i⁽²⁾    ;

σ z

¹      _Σ^∞

2πh² 2(1 – 2ν) ^{j = 1}

_λ(2) ^j sin2^λ₂^j(2)

K₀   ^{λ j}  r [(1 – ν)g_i⁽²⁾ – νf_i⁽²⁾];

h

=   1    3

^rz 2πh 2r

_z2   _{6         1          ∞ λ}(2)         _λ(2)

.    +              Σ j K j h r 2(1 – 2ν) j = 1      λj(2)        h sin2

r d d z [(1 – ν) g_i⁽²⁾ – νf_i⁽²⁾]

Набор произвольных постоянных с, с₁, с₂ служит для удовлетворения граничным условиям на боковой цилиндрической поверхности. Эти граничные условия могут быть поставлены либо на линии боковой поверхности, либо интегрально.

Например, для круглой пластинки радиуса а, защемлённой по контуру, w = 0;       0 = 0; u = 0 при r = а, где w0 и u0 — перемещения точек срединной плоскости:

1 2v 1    1 v

^U0= 8vn G ' r 2v cr^:

w₀

3(1 – ν )

4πG h³

r² lnr +

1 – ν c r2

2ν 1

+ c₂

3(8 – 3ν) _{4 0 π G h}

lnr –

1               ∞       λ⁽²⁾           λ⁽²⁾                   dg⁽²⁾

Σ ^j K₀^j r 2(1 – ν) ⁱ

4πG 2(1 – 2ν) j = 1    2 λj(2)       hdz sin 2

df_i(2)

dw 3(1 – ν)         1     1 – ν 3(8 – 3ν)1

0 = –          r lnr +    + c r – dr       4πGh3         2 ν 1     40πGhr

+

4πG 2(1 – 2ν)

∞ Σ j = 1

_λ(2) ^j sin2^λ₂^j(2)

_λ(2)

K1 h^j r 2(1 – ν)

^{d g i(2)} dz

df_i(2)

d z

z = 0

Перемещения, удовлетворяющие условиям защемления:

3(1 – ν)      r    3(1 – ν)     r2            1 – 2ν r2 ln    +            a 2     –1 + z

4πGh3      a 8πGh3     a2        4(1 – ν)πGa

3(8 – 3ν)      r lnr

40πGh     a

3ν      r      3ν ln +

2πGh³    a    4πGh³

1 – 2ν 1

.        1

8νπG r

∞1

Σ j = 1 4πG 2(1 – 2ν)

r²

_a 2

+ z

3(1 – ν)

_{2 π G h} 3

rlnr

sin2^λ₂^j

^K0

_λ(2)

j r h

2(1 – ν)

_{d g i}(2) dz

^{3(8 – 3 ν )} . ^r + ^{9(6 – ν )} . ¹

40πGh^.a²     40πGh^.r

^{d f i(2)} ; dz

2 – ν 1             1 – 2ν      ∞     λ⁽²⁾        λ⁽²⁾

^.    +                        Σ ^j K ^j r f⁽²⁾

2πGh   r    4πGh 2(1 – 2ν) j = 1    2 λj(2)      h sin 2

Для свободно опёртой круглой пластинки граничные условия могут быть поставлены в следующем виде:

h/2

w₀ = 0;              ∫ σ_rdz = 0;

-h/2

h/2

∫ σ_rzdz = 0;        при r = a.

-h/2

Перемещения, удовлетворяющие условиям свободного опирания пластинки:

3( 1 V)Jr + 3(3 + v)(1 - v)a2p ) _-z1 - 2v . J_ _-3(8 3v)_r 4n Gh³      a     8(1+ v)n Gh³ U² ) id v)n G a²    40n Gh a

– z²

3ν r      3ν(1 – ν)

ln +

4πGh³    a 4(1 + ν)πGh³

u =

1 – 2 ν 8νπG

r

1 +

1 – ν

1 + ν

r²

_a 2

¹      ^  ¹   K f j

4nG^2d 2v>j = 12°h

"      2

+ z

3(1 – ν)     r

_{2 π G h} 3 ^{r ln}_a

r_ ^(1 — v)

dz

^{3(1 – ν )}r + ^{9(6 – ν )} . ¹

2πGh(1 + ν)     40πGh^.r

fl dz

^{2 – ν}. ¹ +          ^{1 – 2 ν}      Σ^{∞     λ j(2)}K   ^{λ j(2)}r f⁽²⁾

²πGh³r 4πGh 2(1 – 2ν) ^{j = 1} s_in₂^λj⁽²⁾      h

местное напряжённо-деформированное состояние

Полученные функции, описывающие напряженно-деформированное состояние упругого слоя при действии сосредоточенной силы, состоят из двух частей. Первая часть — классическое решение в форме А. Лява — характеризует напряжённо-деформированное состояние, распространяющееся по всей пластине. Произвольные постоянные в этом решении служат для удовлетворения граничным условиям на боковой поверхности. Следует отметить, что основная часть решения А. Лява совпадает с решением, которое дает классическая теория изгиба пластинок, построенная на гипотезе Кирхгофа, что позволяет в случае, если размеры пластины в плане велики по сравнению с толщиной (  << 1),

a описывать общее напряжённо-деформированное состояние с помощью решений классической теории пластинок.

Вторая часть функций представлена рядами по собственным функциям краевых задач. Зависимость членов ряда от координат в плоскости пластинки определяется модифицированными функциями Бесселя второго рода (в литературе встречаются и другие названия этих функций: функции Бесселя мнимого аргумента второго рода, функции

Макдональда) нулевого и первого порядков. Функции K0(х), K1(х) быстро убывают (по экспоненциальному закону) с ростом модуля аргумента x. В соответствии с этим напряжённо-деформированное состояние, характеризуемое рядами, имеет характер точечного краевого эффекта и быстро затухает по мере уда- ления от точки приложения нагрузки.

Дифференциальный оператор, описывающий краевую задачу, является несамосопряжённым [6]. Поэтому его собственные значения λj(k) — корни трансцендентных уравнений (9) — комплексные. Комплексными являются также собственные функции (7), включая их составную часть

функции

( X\k-' j

K_{0 h} r

,

_λ(k) ^j

K_{1 h} r

Однако, то обстоятельство, что собственные значения — попарно сопряжённые комплексные числа, следовательно, попарно сопряжёнными являются соответствующие значения собственных функций (7), функций Макдональда и их произведений, делает сумму ряда вещественной.

Первые пять значений корней уравнений (9) — λ_j⁽¹⁾ и λ_j⁽²⁾ — приведены в таблице.

Как видно из таблицы, модули собственных значений возрастают с ростом номера собственного значения, что обуславливает хорошую сходимость рядов и позволяет ограничиться суммой трёх-четырёх пар членов ряда.

j 1 2 3 4 5 λ(k) j k = 1 4,212±i2,251 10,713±i3,103 17,073±i3,551 23,398±i3,859 29,708±i4,090 k = 2 7,498±i2,769 13,900±i3,352 20,239±i3,717 26,555±i3,983 32,860±i4,193 местное напряжённо-деформированное состояние при действии произвольной нагрузки

Функции, описывающие точечный краевой эффект вблизи действия сосредоточенной силы, построенные в виде разложений по собственным функциям несопряжённого дифференциального оператора, описывающего краевую задачу (5), (6), в декартовой системе координат записываются следующим образом:

x 1 – 2ν    ∞      λj⁽²⁾         λj⁽²⁾

u⁽x, y, z⁾= 4πGh    2(x² + y²) j^Σ= 1     λ⁽²⁾K¹h    ⁽x⁺y⁾f^{i ;}

sin2 2j y 1 - 2v   -    \(2)     p7:2) ,--------V

v(x. У- z) - 4n_Gh    2(x2 + y2)^1     _x(2) K 1  h  A⁽x^{2 +}y² ) J f^;

sin2 2

w (x, y, z) = –

4πGh 2(1 – 2ν)

∞ Σ j = 1

_{1              λj}(2)

_λ( 2 ) ^K0  _h    ( x² + y²)

sin²₂^j

2(1 – ν)

_dgj(2) _{d z}

_dfj(2) _{d z}

Если в области х, y∈s действуют эквивалентные силы Р(х, у), то упругие перемещения могут быть найдены интегрированием соответствующих функций по области s:

x 2 2v                 ”      ^Xj-²⁾       f ^Xj-²⁾ I)

u = 4nGh J 2( x² + y²) 17P(x', y')Д     X(2) K¹ l~h"" ^⁽x^-x')^{+ (y -}y')²) ^{f(2) dx}'^dy';

j sin2 2

y        1 – 2ν                 ∞      ^λj^{(2)         λ}j⁽²⁾

v =_{4πGh    2(x2 + y2)}∫_s∫P(x′, y′) _jΣ_{= 1 λ (2)}K_{1   h}   ( x – x ′ )² +( y – y ′ )²  f_i⁽²⁾dx′dy′;

^s                 sin²₂^j

1∞ w =–                 ∫∫P(x′, y′) ς

4πGh 2(1 – 2ν) ^{s          j = 1}

_{sin2 λ j(2)}K₀

_λ(2) j

h

x ′ )² +( y – y ′ )^{2 2(1 – ν )}_{d z}^j

_dgj(2)    _df_j(2)

^–_{d z}   dx′dy′.

Компоненты тензоров деформаций и напряжений определяются по известным формулам теории упругости:

∂u       ∂v∂ x   ∂x ;    y   ∂y ;    z∂

ε

xy

• 1    dUu    ду ।              1 f dvdw)

+     ; e =         +;

• 2    (dy   дx J       ^yz 2 (dz   дy )

= 1 d6 w   д u\ e : "2 (ax + az"/

γ_ху = 2 ε_ху;      γ_уz = 2 ε_уz;    γ_zх = 2 ε_zх;

E

σ_x = _{1 –} ν2[ε_x + ν(ε_y + ε_z)];

σ =       [ε + ν(ε + ε )];

^y 1 – ν^{2 y z x}

E

σ_z = _{1 –} ν₂[ε_z + ν(ε_y + ε_x)];

τ_ху = G γ_ху; τ_уz = G γ_уz;   τ_zх = G γ_zх.

заключение

На основе трёхмерных уравнений теории упругости получено явное решение краевой задачи о действии сосредоточенной силы на упругий слой, описывающее точечный краевой эффект. Решение построено как разложение по собственным биортогональным функциям вспомогательной несамосопряжённой краевой задачи в виде быстросходя-щихся рядов. Функции, формирующие ряд, дополняют классическое решение краевым эффектом, быстро затухающим по мере удаления от точки приложения силы, что обеспечивается экспоненциальным законом убывания функций Макдональда.

Решение для сосредоточенной силы в качестве функции влияния использовано в задаче о произвольном локальном нагружении упругого слоя. Компоненты вектора перемещений получены в виде определённых интегралов по области действия нагрузки. Компоненты тензоров деформаций и напряжений получаются в соответствии с известными формулами теории упругости дифференцированием функций перемещений.