ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN

На сегодняшний день в задачах обработки металлов давлением одной из важнейших является определение напряженно-деформированного состояния тонкостенных труб обжимом, что позволяет выявить силовые характеристики процесса, технологические возможности и рассчитать изменение толщины заготовки. Примем, что тонкостенными трубами будут являться те, у которых толщина стенки не превышает 0,1 радиуса срединной поверхности трубы. Достаточно часто данные задачи решаются для простейшей формы оснастки, когда форма матрицы или пуансона является конической или образующая их рабочий контур имеет постоянный радиус кривизны [1–5]. Причём рассматривается идеально жесткопластический материал или материал с линейным упрочнением, а так же, как правило, пренебрегают изменением толщины заготовки в процессе деформирования. Достаточно много вопросов посвящено оценке технологических возможностей реализации процесса обжима [6; 7].

Теоретическое и экспериментальное исследования процесса обжима в зависимости от параметров оснастки исследовались в работе [8]. Особенности технологий обжима заготовок с учетом формуемого материала исследовались в труде [9]. Вопросы ограничений при обжиме толстостенных заготовок изучались в работе [10]. Исследования, посвященные экспериментальным работам по совмещению операций обжима и раздачи, отражены в работе [11]. Также проведено много экспериментальных исследований, посвященных оценке влияния коэффициента трения на значения деформаций при обжиме и раздаче. Влияние анизотропии механических свойств на деформированное состояние трубных заготовок, а также оценка потери устойчивости заготовки в процессе формоизменения рассмотрено в работе [12]. Кроме того, вопросы проблемы потери устойчивости при обжиме рассматривались в работе [13; 14]. Помимо потери устойчивости, в процессе обжима одной из проблем являются недопустимые утонения заготовки, что рассматривается в работе [15].

В последнее время значительное количество работ посвящено исследованию ротационного обжима, в работах [16; 17] предложены различные машины и технологии для реализации данного процесса с оценкой изменения толщины заготовки и степени деформации. В исследовании [18] проведена оценка шероховатости, твердости поверхности заготовки при ротационной вытяжке. Автоматизация процесса ротационного обжима заготовки рассмотрена в работе [19].

В связи с развитием численных методов широкое распространение для оценки напряженно-деформированного состояния получили метод конечных элементов. Конечно-элементное моделирование некоторых осесимметричных задач обжима рассмотрено в 2D-постановке

[20]. Методом конечных элементов рассмотрены различные силовые режимы традиционного обжима и обжима с противодавлением [21]. Одним из наиболее эффективных методов решения задач нелинейной пластичности является метод переменных параметров упругости, особенности применения которого отражены в трудах [22; 23].

Следует отметить, что вопросы анализа напряженно-деформированного состояния деталей в задачах обработки давлением достаточно подробно рассмотрены в трудах [24; 25]. Модели неупругого деформирования материалов, физические теории пластичности, которые особенно актуальны в задачах пластического формоизменения, рассмотрены в работах [26; 27]. В исследовании [28] предложена система уравнений для описания деформирования тонкостенных заготовок в процессе обжима и раздачи. Исследование схоже с проблематикой данной статьи, однако в ней рассматривается жесткопластическая модель материала при условии несжимаемости. Предлагаемый в данной статье подход при принятых допущениях позволяет учесть сжимаемость материала при упругопластическом деформировании.

Методика исследования

Таким образом, рассмотрим криволинейную матрицу, у которой образующая её рабочий контур задаётся произвольной функцией. Решение аналогичной задачи было представлено в работе [7], где моделирование процесса обжима трубы выполняется численным интегрированием уравнений равновесия методом Рунге – Кутта второго порядка. В основе расчётно-аналитической модели определения напряжённо-деформированного состояния данного исследования лежит метод переменных параметров упругости [3; 29], который позволяет учитывать изменение толщины в процессе деформирования, нелинейный закон упрочнения, анизотропию и сжимаемость материала.

Применение численного метода переменных параметров упругости требует задания аналитической зависимости между интенсивностью напряжений и интенсивностью логарифмических деформаций в соответствие с гипотезой единой кривой. Согласно существующим методам аппроксимации диаграмм деформирования, предлагаемым Н.Н. Малининым [3] и др. исследователями [30; 31], можно отметить, что обычно диаграмма деформирования для алюминиевых и титановых сплавов хорошо аппроксимируется линейно-степенной зависимостью:

[ 3 Ge i при e i <  e iT , ° i = i

[Ke" при ei > eiT, где G – модуль упругости второго рода; eiT – интенсивность логарифмических деформаций, соответствующая переходу упругого деформирования в пластическое; K и n – параметры кривой упрочнения.

Схема деформирования тонкостенных труб с использованием оснастки сложной формы при обжиме изображена на рис. 1. В общем случае при обжиме кривая, образующая рабочий контур матрицы и пуансона, может иметь знакопеременный радиус кривизны.

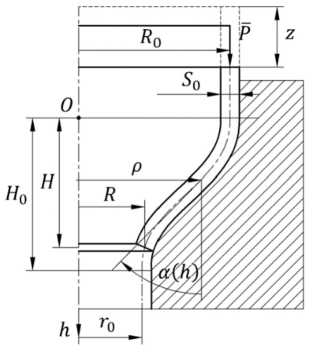
Рис. 1. Схемы обжима трубных заготовок с использованием криволинейной осесимметричной оснастки

Fig. 1. Schemes of crimping pipe blanks using curved axisymmetric tooling

Если использовать безмоментную теорию оболочек, уравнения равновесия при обжиме тонкостенной трубной заготовки в осесимметричной матрице с учётом удельной силы трения и удельного давления, действующих со стороны оснастки, в проекции на касательную и нормаль к поверхности рассматриваемого элемента можно представить в следующем виде [3; 27]:

d                q mp P _n

(°mp5) °5 + dp               sin a   an m । 6

R m   R." 5 ’

где ° _m - меридиональное главное нормальное напряжение; °₆ - окружное главное нормальное напряжение; q -контактное давление, действующее со стороны матрицы по нормали к рассматриваемому элементу оболочки; R_m – меридиональный радиус кривизны срединной поверхности оболочки; R g - окружной радиус кривизны срединной поверхности оболочки; q_mp _ f_mpq - удельная сила трения, действующая со стороны оснастки на рассматриваемый элемент оболочки; f_тр – коэффициент трения; S - переменная толщина оболочки; a - угол между касательной к элементу оболочки и её осью симметрии, отсчитываемый по часовой стрелки; р - радиус окружности срединной поверхности оболочки в сечении перпендикулярном оси оболочки.

Окружной радиус кривизны срединной поверхности оболочки определяется по формуле

R ₀ = р / cos a .                     (2)

Для определения меридионального радиуса R_m выразим кривизну оболочки в меридиональном направлении к _m через a и р :

Интенсивность напряжений a i и интенсивность логарифмических деформаций e_i определяются выражениями:

• I    m m mm 0     0 ^;

  к

  
  

  m

  
  

  R m

  
  

  d a . .

  --sin a .

  d р

  
  
  
  

  2 222 e i = "Г e m ^- e 0) ⁺ ( e 0 - e z ) ⁺ ( e n ^- e m ) .

  
  

Знак (–) минус в уравнении (3) учитывает тот факт, d ^a^n что для выпуклой оболочки всегда-- < 0 .

d р

Используя уравнения (2) и (3) и определяя удельное давление q , действующее со стороны матрицы, как функцию a и р , можно представить систему (1) в виде выражения:

d ( a )       ⁺ ctg ^{a ) -a} m ^{+  р} ^ J S  ₍₄₎

d р                   р

Проинтегрируем уравнение (4), используя уравнения связи напряжений и деформаций для плоского напряженного состояния в виде:

где e_n – логарифмическая деформация по толщине заготовки.

Деформация по произвольному направлению V согласно тензору деформаций Генки определяется уравнением:

eV = em^m + e0^0 + en^2 , где Xm, Х0, Xn - направляющие косинусы вектора V .

С учетом плоского напряженного состояния, уравнений метода переменных параметров упругости логарифмическая деформация по толщине (нормальная составляющая) примет вид:

en

*

Т    ТТ⁽ e m ^{+ e} 0 ) ,

^{( 1 -}ц )

E ^*

^{a m} =Fv2)

E ^*

^G0 = ( 1 -ц * ² )

( e m ^{+ Ц} e 0 ) ;

( e 0 ^{+ Ц} e m ) ,

,

и, учитывая, что деформируемый край трубы свободен, получим интегральное уравнение равновесия в деформациях для обжима:

*

e m = -U e 0

( 1 -ц" ² )

E *^S р exp ( f _T ^a )

J'

R

E*^S ( 1 ^{+ f} _Tctg ^a ) exP ( ^f _T ^a )

( e 0 ⁺P ‘ e m ) ^d р

где e_m – меридиональная логарифмическая деформация;

e ₀ - окружная логарифмическая деформация; E * и ц * -переменные параметры упругости; R – радиус деформируемого наружного края трубы (см. рис. 1).

Переменные параметры упругости определяются выражениями [3; 29]:

1 - 1 — 2 Ц E

E‘ =_____ E _____; и * = ^{2    3 E} "

1 + 1 ^{2 ц} E         1 + 1 2^ц E

_{3 E}   сек               _{3 E} сек

где E - модуль упругости первого рода; ц - коэффициент Пуассона; E сек = a / e i - секущий модуль.

тогда деформация по направлению V будет определяться уравнением:

n   m_mm_m   ^0^,v0

*

ц

^{( 1 -ц} * )

⁽ e m ⁺ e 0^{) X} n ■

Условие перехода рассматриваемой точки тела из упругого состояния в пластическое определяется условием пластичности Губера – Мизеса ai = Vam2 -ama0+a02 = aT ■

Процесс обжима будем рассматривать в общем случае, когда кривая, образующая рабочий контур матрицы, задаётся произвольной функцией, определяющей положение деформируемого элемента по радиусу в зависимости от его положения по длине деформируемой части трубы р = р ( h ) (см. рис 1), где h - координата, которая отсчитывается от точки на оси симметрии, соответствующей краю криволинейного участка матрицы и направлена в сторону направления нагрузки.

Тогда переменный угол между касательной к элементу оболочки и её осью симметрии, зависящий от h , можно определить следующим образом

a = a ( h ) = arctg

d р dh

Поскольку при увеличении h радиус при обжиме уменьшается, следовательно: d р = - tg [a ( h ) ] dh . Согласно вышесказанному, а также учитывая, что при

обжиме окружные деформации можно считать известными и зависящими только от положения рассматриваемой точки в очаге деформации

1 fp(h)1 eg = lnl I, кую функцию, которая охватывает полупериод синусоиды, обеспечивая плавный вход цилиндрической трубы в зону деформирования и плавный выход с образованием цилиндра другого радиуса. Для обжима данную функцию можно записать в виде уравнение (5) можно записать согласно [32] в виде

R -     f   I

P ( h ) = ⁽ 0g ⁰ ) [cosl- h -К I-1] + R o,        (11)

• 2       l H 0 )

  ^h

  H

  
  

  * P ( )

  e m = -P ln l I -

  
  

  ( 1 -И- )

  E' S p ( h ) exp ( f ,n ( h ) )

  
  

  E * S ( tg [a ( h ) ] + f „) exp ( f .a( h ) ) f fp ( h ) A    *

  ln        +u e,

  ( 1 -o '² )              ll R J

  
  

  dh

  
  

  , (7)

  
  

  где H – положение края деформируемого участка трубы (см. рис. 1).

  Поскольку в расчетах матрицы на прочность или выборе необходимого вида смазки требуется знать величину контактного давления, тогда значение давления будем определять, используя второе уравнение равновесия системы (1):

  
  

  где (см. рис. 1) R ₀ – радиус срединной поверхности трубы на входе в матрицу; r ₀ – радиус срединной поверхности трубы на выходе из матрицы; H ₀ – полная длина криволинейного участка матрицы, равная длине полупериода синусоидальной функции (11).

  Поскольку уравнения (11) определяют геометрию срединной поверхности трубы при деформировании, то с достаточной степенью точности можно считать, что геометрию матрицы при обжиме можно получить, прибавляя поправку на половину толщины стенки трубы:

  
  

  P М ( ^h ) =

  
  

  ^{( R} 0 ^r o )

  
  

  I ^h     I                 ^S 0

  ^[cos | Тт^-^ I ^{- 1] +} R 0 ⁺ "V’

  l H 0 )           ²

  
  
  

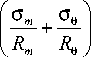
  S = q m ⁺ q e ’

  
  
  
  

где S ₀ – исходная толщина стенки трубы.

Угол между касательной к элементу оболочки и её осью симметрии (см. рис.1), будем определять согласно (6)

где q m - составляющая контактного давления от действия меридионального напряжения; q _e - составляющая контактного давления от действия окружного напряжения.

Если уравнение профиля матрицы задано в виде дифференцируемой функции р = р ( h ) , то радиусы кривизны будут определяться согласно формулам:

2V

L f d P I    I dP I „ _

J 1 +1 — I    l I  ’ Re =/—7 •

\ l dh ) l dh )        cos a ( h )

В этом случае выражения, определяющие составляющие контактного давления, можно представить в следующем виде:

_ d P qm = О m —7 dh т I-3

cos a ( h

------S ( h ) .               (10)

P

В работе [32] предложен подробный порядок решения задачи об определении напряжённо-деформированного состояния методом переменных параметров упругости с использованием интегральных уравнений равновесия для осесимметричных оболочек.

Рассмотрим решение интегрального уравнения (5) на примере конкретной задачи. Для получения знакопеременного радиуса кривизны, образующей рабочий контур матрицы, возьмём синусоидальную тригонометричес-

( ^R 0 ^- r 0

2 H 0

a ( h ) = arctg

) ^л ■ f h I

— sin —n l H0 )

Кривые, определяющие геометрию матрицы и зоны деформирования трубной заготовки по срединной поверхности при обжиме, построенные по уравнениям (7) и (8), представлены на рис. 2.

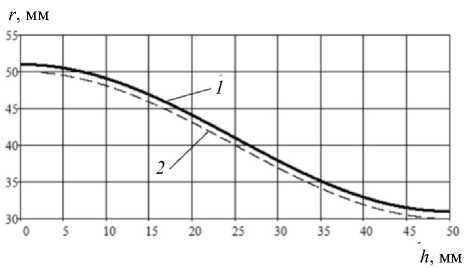
Рис. 2. Геометрия матрицы и зоны деформирования трубной заготовки по срединной поверхности при обжиме: 1 – геометрия матрицы; 2 – геометрия срединной поверхности

( R ₀ = 50 мм; r ₀ = 30 мм; S ₀ = 2 мм; H ₀ = 50 мм)

Fig. 2. Geometry of the matrix and the strain zone of the pipe billet along the median surface during crimping: 1 – geometry of the matrix; 2 – geometry of the median surface

( R ₀ = 50 мм; r ₀ = 30 мм; S ₀ = 2 мм; H ₀ = 50 мм)

Радиус срединной поверхности трубной заготовки R0 принимался равным 50 мм, толщина S0 – 2 мм. Для материала Д16 механические свойства были заданы в соответствии со стандартом ГОСТ 18482-2018 [33] и справочными данными алюминиевых сплавов: предел прочности Ов = 390 МПа ; условный предел текучести О0 2 = 255 МПа ; относительное удлинение 5 = 12 %; модуль упругости E = 72000 МПа ; коэффициент Пуассона Ц = 0,33. Диаграмма деформирования в соответствии с принятой линейно-степенной аппроксимацией, была построена по методике, изложенной в работах [34; 35].

Результаты исследования и их обсуждение

Распределения напряжений и деформаций трубы при обжиме в криволинейной осесимметричной матрице (см. рис. 2) представлены на рис. 3, 4. Следует отметить, что аналогичные результаты исследования, но для процесса раздачи заготовки, представлены в работе [36]. На рис. 5 показано изменение толщины заготовки, определяемое выражением S = S ₀ exp ( e n ) . На рис. 6 приведены результаты расчета изменения составляющих и полного контактного давления со стороны матрицы, определяемые по формулам (8)–(10).

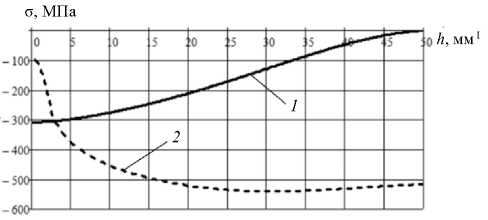
Рис. 3. Напряжённое состояние трубы при обжиме в криволинейной осесимметричной матрице: 1 – меридиональные напряжения О m ; 2 - окружные напряжения О₀

Fig. 3. The stress state of the pipe during crimping in a curved axisymmetric matrix: 1 - meridional stresses Оm ; 2 - circumferential stresses O0

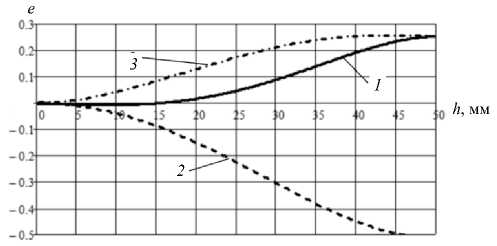
Рис. 4. Деформированное состояние трубы при обжиме в криволинейной осесимметричной матрице: 1 – меридиональная логарифмическая деформация e_m ; 2 – окружная логарифмическая деформация e ₀ ; 3 - логарифмическая деформация по толщине e_z

Fig. 4. Strain state of the pipe during crimping in a curved axisymmetric matrix: 1 – meridional logarithmic strain em ; 2 – circumferential logarithmic strain e0; 3 - logarithmic strain in thickness ez

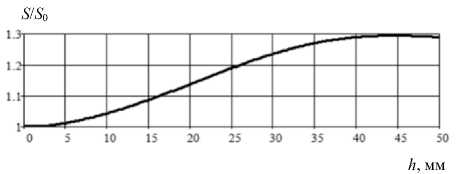
Рис. 5. Изменение относительной толщины стенки трубы при обжиме в криволинейной осесимметричной матрице

Fig. 5. Change in the relative thickness of the pipe wall during crimping in a curved axisymmetric matrix

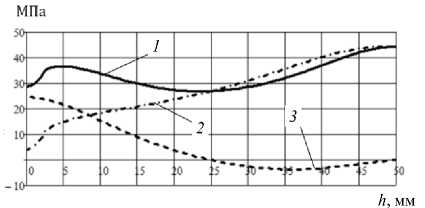
Рис. 6. Изменение контактного давления при обжиме в криволинейной осесимметричной матрице: 1 – полное контактное давление q ; 2 – составляющая контактного давления от действия окружного напряжения q ₀ ; 3 - составляющая контактного давления от действия меридионального напряжения q_m

• Fig. 6.    The change in contact pressure during crimping in a curved axisymmetric matrix: 1 – the total contact pressure q ; 2 – the component of contact pressure from the action of the circumferential stress q ₀ ; 3 - the component of contact pressure from the action of the meridional stress q_m

Для оценки точности решения методом переменных параметров упругости проводилось сравнение положения значений интенсивностей напряжений и деформаций, определяющих напряженно-деформированное состояние, на диаграмме деформирования. Согласно рис. 7 все точки, характеризующие напряженно-деформированное состояние при обжиме, лежат на диаграмме деформирования. Соответственно, процесс последовательных приближений сходится, и получено решение с заданной точностью.

На рис. 3–7 представлены характеристики напряжённо-деформированного состояния трубы при обжиме для случая, когда труба проходит всю зону деформирования, и область интегрирования определяется от H ₀ до 0. Если рассматривать процесс деформирования поэтапно, изменяя положение деформируемого края трубы H в сторону увеличения до H ₀ , то можно определить изменение технологических параметров, таких как усилие деформирования на протяжении прохождения всего процесса. Перемещение точки Z приложения усилия деформирования к трубной заготовке относительно матрицы связано с положением деформируемого края трубы H условием равенства смещенных объёмов

z ( h )=_1   H p( h > s। h। dh.

R 0 5 0 о cos a ( h )

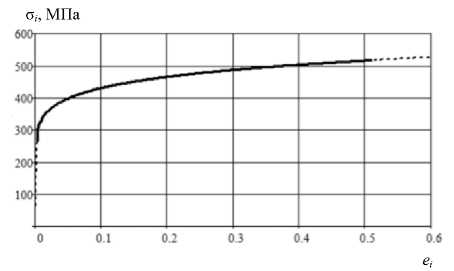
Рис. 7. Положение значений интенсивностей напряжений и деформаций, определяющих напряженно-деформированное состояние трубы при обжиме, на диаграмме деформирования

• Fig. 7.    The position of the stress and strain intensities that determines the stress-strain state of the pipe during crimping on the deformation diagram

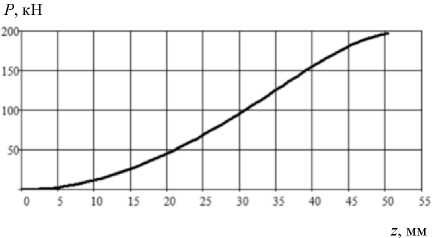
Рис. 8. Изменение усилия деформирования при обжиме трубы в криволинейной осесимметричной матрице от перемещения точки приложения усилия

• Fig. 8.    Change in the strain force when crimping a pipe in a curved axisymmetric matrix from the displacement of the point of application of the force

Усилие обжима P ( Z ) определяется величиной максимального меридионального напряжения о mh = ₀ ( Z ) в точке 0 в зависимости от перемещения Z

P ( Z ) = 2 n R о 5 о |о mh = 0 ( Z )| .

На рис. 8 представлен график изменение усилия деформирования при обжиме трубы в криволинейной осесимметричной матрице от перемещения точки приложения усилия.

Заключение

Таким образом, в рамках данного исследования предложена модель процесса обжима тонкостенной трубы в криволинейной осесимметричной матрице, которая позволяет рассчитать напряжения и деформации при деформировании трубы, оценить изменение толщины, величину контактного трения с учётом нелинейного закона пластичности материала, определить изменения усилия обжима в зависимости от перемещения точки приложения усилия. Предложенная методика и полученные соотношения могут быть эффективно использованы для расчетов процесса обжима в осесимметричных матрицах различной формы, например S -образный профиль, образованный дугами окружностей разного радиуса на вогнутом и выпуклом участке, имеющих общую касательную в точке перегиба, или конический профиль с выпуклым участком на входе в матрицу и вогнутым на выходе. Результаты исследования могут найти применение в области обработки металлов давлением при изготовлении оболочечных элементов авиационного назначения. Также следует отметить, что рассматриваемая методика может быть использована при исследовании напряженно-деформированного состояния заготовок при раздаче, однако в этом случае будут различаться определяющие соотношения.