Настройка импульсных погодных регуляторов отопления зданий

Очевидно, что, когда фактическая мощность системы отопления W_СО является избыточной для данных погодных условий, в здании устанавливается некоторая максимальная температура t_В ^MAX , которая, естественно, будет превышать свое заданное значение t ^З _В . Понятно, что такая ситуация имеет место как в период «срезки» графика централизованного регулирования [1, 2], так и в любой другой период, так как «…построение графика ориентировано на обезличенное здание … при расчетной температуре внутреннего воздуха 18 °С» [2, с. 458], и в связи с этим погодный график для данного конкретного здания может быть «плохим» [3, 4]. Кроме того, к этой же ситуации также следует отнести и случай плохо настроенного нерегулируемого узла смешения как насосного, так и элеваторного.

В таком случае с целью обеспечения приемлемой температуры внутреннего воздуха зданий и экономии расхода теплоты целесообразно применение импульсного режима отопления, при котором в течение некоторого периода длительностью T система отопления включается на полную мощность WСО только на время γ T , а в течение времени (1 - γ)T находится в отключенном состоянии. При этом возникает вопрос: как следует выбирать скважность управляющих импуль- сов γ и длительность периода T , чтобы температура внутри здания поддерживалась в заданных пределах?

Требуемое значение скважности управляющих импульсов γ можно определить, исходя из следующих соображений. Согласно закону сохранения энергии в стационарном режиме мощность системы отопления W_СО должна равняться тепловым потерям здания при той температуре, которая установилась внутри него, и при той температуре, которая наблюдается снаружи. Когда мощность системы отопления W_СО избыточна и при этом система отопления работает в режиме постоянного включения, то в здании устанавливается некоторая максимальная температура t_В ^MAX , если в этом случае для оценки потерь теплоты использовать формулу Н.С. Ермолаева, то получим, что

W_СО = q_V(t_В ^MAX - t_Н)V , (1)

где tН – температура наружного воздуха, qV – удельная тепловая характеристика здания, а V– его объем. В случае же, когда скважность импульсов подобрана должным образом, получим, что

γ W_СО = q_V(t ^З _B - t_Н)V . (2)

Здесь у W_co - средняя за период T мощность системы отопления в импульсном режиме. Разделив уравнение (2) на уравнение (1), получим, что скважность импульсов необходимо определять по следующему соотношению:

^Y = (t B - t H ) / (t MAX - t H ) .                     (3)

Максимальную температуру внутреннего воздуха t_В ^MAX можно определить по математической модели теплового режима здания (ТРЗ), которая, конечно, предварительно должна быть настроена на реальный процесс, т. е. должна быть решена задача параметрической идентификации модели по экспериментальным данным [5]. Это можно сделать, в частности, и по математической модели стационарного режима, которая представляется уравнением (1). Для этого только нужно иметь в виду, что мощность системы отопления, как это нетрудно показать, можно определить по следующей формуле:

W CO = ^(kF) CO ^(t CO - t H ) /

/[1 + (kF) co / (q v V) + (kF) co / (2cG^)],    (4)

где c– теплоемкость единицы массы теплоносителя, tСО – температура воды на входе системы отопления, (kF)СО – произведение коэффициента теплопередачи на площадь поверхности теплообмена для всей системы отопления, это тот параметр, который подлежит определению при идентификации модели системы отопления, GСО – массовый расход теплоносителя через систему отопления.

Подставляя данное выражение в (1), найдем из него формулу для вычисления t_В ^MAX :

t MAX = t H + (kF)_C0(t_C0 - t H )/

/[(q v V) + (kF) co + (kF) co / (2cG co ) ■ (q v V)], (5)

а затем, подставляя соотношение (5) в уравнение (3), и требуемую скважность управляющих импульсов у :

Y = ⁽t^B - t H ) x

^(t co - t H )

x [1 + (q v V)/(kF) co + (q v V) / (2cG co )].    (6)

Из формулы (6) видно, что скважность управляющих импульсов y является функцией t B , t_H, t_co и G_co . Кроме того, скважность y также зависит и от теплозащитных свойств и размеров здания – параметра (q_VV) , а также и от характеристики системы отопления – параметра (kF)_СО .

На рис. 1 для трех значений температуры на входе системы отопления tСО указаны графики зависимости скважности управляющих импульсов Y от температуры наружного воздуха tH : кривая 1 для tco = 70 °c, кривая 2 для tco = 50 °Cи кривая 3 для tco = 30 °c. При этом вычисления производились по формуле (6) при qV = 0,168 Вт / (м3 ■ °c),      (kF)co =1680 Вт / °c, tB = 18 °c, V=1700 м3, Gco =1,57кг/с.

Дифференцируя формулу (6) по температуре наружного воздуха tН , получим, что dY = (tB -tco) d tH (tco - tH)2

x [1 + (q V V)/(kF) co + (q V V)/(2cG co )] < 0 . (7)

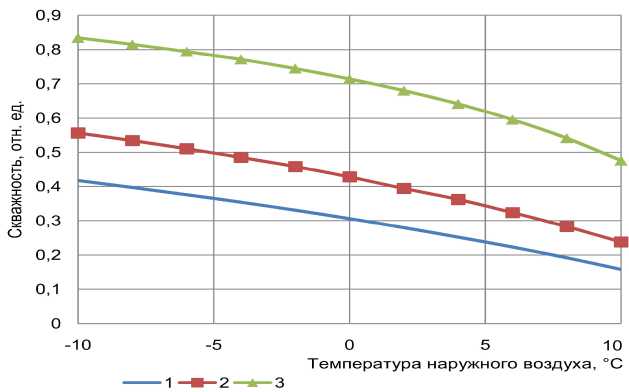
Рис. 1. Кривые зависимости скважности управляющих импульсов Y от температуры наружного воздуха t_Н

Из формулы (7), а также и из рис. 1 следует, что с увеличением температуры наружного воздуха t_H скважность управляющих импульсов у уменьшается, что согласуется и с простыми физическими соображениями: чем теплее на улице, тем меньше теплопотери здания, тем меньшее количество теплоты требуется для отопления здания.

Кроме того, непосредственный анализ формулы (6) показывает, что скважность управляющих импульсов у растет в следующих случаях:

• 1)    с ухудшением теплотехнической характеристики системы отопления – с уменьшением параметра (kF)_СО и, вследствие этого, мощности (теплового потока) системы отопления;

• 2)    с увеличением параметра (q_VV) , т. е. с ухудшением теплозащитных свойств здания и увеличения, вследствие этого, его тепловых потерь;

• 3)    с уменьшением температуры воды на входе системы отопления;

• 4)    с уменьшением расхода воды G_СО через систему отопления.

Из формулы (6) видно, что для вычисления скважности управляющих импульсов у требуется измерять температуру наружного воздуха t_Н , температуру воды на входе системы отопления (после элеваторов или каких-либо других нерегулируемых узлов смешения) t_СО , а также и расход воды через систему отопления G_СО [6, 7]. Схема системы управления, реализующей данный алгоритм импульсного управления, приведена на рис. 2.

Если же по каким-то причинам удобнее изме- рять температуру tC и расход GC сетевой воды в подающей магистрали, то в этом случае мощность системы отопления WСО следует выразить через температуру tC , как это сделано в [3, 4].

Данное соотношение имеет вид

W СО

_cG          ^(t c - t H )

^C x + 0,5 + cG C + cG_C ’ 1 + X + (kF) co + q V V

где x - коэффициент смешения. Схема импульсной системы управления для случая измерения таких величин приведена на рис. 3.

Для определения длительности периода следования импульсов T можно использовать способ, предложенный в работе [8]. Способ обеспечивает указанную погрешность А ³ поддержания заданной температуры внутреннего воздуха t ^З _В после окончания переходного процесса, т. е. в установившемся режиме. В данной работе для решения этой же задачи предлагается использовать несколько иной подход, как нам представляется, более «прозрачный» и простой.

Как известно [9, 10], динамические свойства ТРЗ можно описать следующим дифференциальным уравнением:

T B di ^ ^ ^ ) + 1 в ( - ) = t M ^AX . (9) d т

Здесь TВ – постоянная времени. Предположим, что в установившемся режиме температура внутреннего воздуха изменяется в соответствии с (9) в зоне tB = tB ±А З. (10)

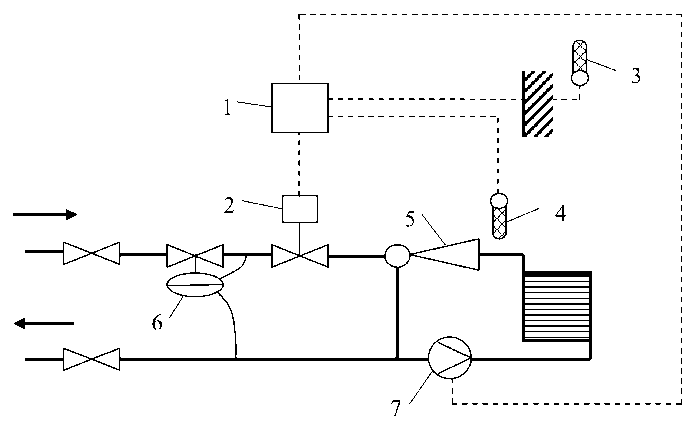
Рис. 2. Схема 1-го варианта импульсной системы управления с измерением температуры воды на входе системы отопления: 1 – контроллер, 2 – двухходовой клапан с электроприводом, 3 – датчик температуры наружного воздуха, 4 – датчик температуры прямой воды, 5 – элеватор, 6 – регулятор перепада давления, 7 – расходомер

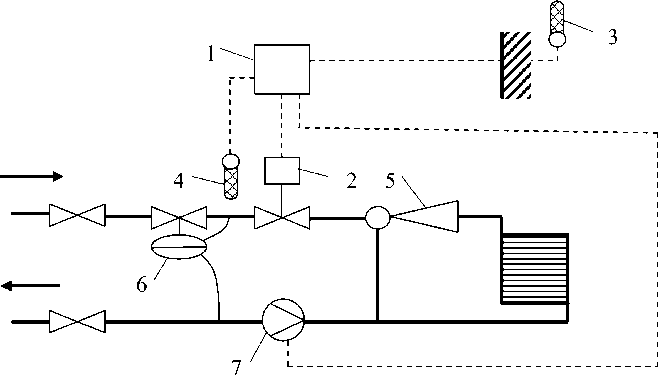
Рис. 3. Схема 2-го варианта импульсной системы управления с измерением температуры сетевой воды

Если свойства объекта управления описываются уравнением (9), то, как это хорошо известно [11, 12], система отопления включится в работу (на нагрев) тогда, когда будет t_B = t B -А ³ , выключится же она тогда, когда будет t_B = t B +А ³ . Решая уравнение (9), для этих условий найдем, что продолжительность времени включения системы отопления т _ВКЛ будет удовлетворять следующему уравнению:

2 А ^З = (t М^АХ - t B +А ^З ) х [1 - exp(- Т вкл /Т в )] • (11)

Из (11) следует, что tВMAX продолжительность времени включения системы отопления тВКЛ будет уменьшаться, что согласуется с простыми физическими соображениями. Кроме того, напрямую из формулы (12) видно, что с увеличением инерционности объекта управления TВ продолжительность времени включения системы отопления тВКЛ, наоборот, будет расти, что тоже хорошо согласуется с простыми физическими соображениями.

Из формулы (12) также следует, что д тВКЛ _ гр       2(tMAX tB)

дА3    В (t^ -tB)2 -(А3)2

^т В ^К Л     ^Т В ^х ln⁽¹    мах з з )

tB   - tB +А

МАХ   З З

_В_____ t B ^А

В    \МАХ fЗ дЗ ) .

t B    ^- t B ^+А

Вспоминая, что скважность управляющих импульсов равна

У = тВКЛ /ТСЛЕД , найдем, что

ТСЛЕД = ТВКЛ / У .

Здесь T_СЛЕД – период следования управляющих импульсов, обеспечивающих удержание температуры внутреннего воздуха в зоне t_B = t B ± А ³ .

Из формулы (12) следует, что

^дт ВКЛ

д t

МАХ В

- Tb х

_______ 2 А ³

(tMAX -tB)2 -(А3)2

Понятно, что для реальных значений аргумен-

тов

^дт ВКЛ

д t ^MAX

< 0, это означает, что с увеличением

Для реальных значений аргументов будет

дт

—^ВКЛ > 0, т. е. с увеличением допустимой по дА ³

грешности поддержания заданной температуры внутреннего воздуха - А ³ как продолжительность времени включения системы отопления т _ВКЛ , так и период следования импульсов будут расти, что также сообразуется со здравым смыслом.

Для вышеприведенных условий определим параметры импульсного управления ТРЗ. Так, если t_co = 50 ° С, а t_H = 4 ° С , то будет t MAX = 42,35 ° С; если же t_co = 40 ° С, а t_H = 4 ° С , то будет t MAX = 34,01 ° С ; если же t_co = 30 ° С , а t_H = 4 ° С , то будет t MAX = 25,67 ° С. Кроме того, будем считать, что t B = 20 ° С , а А ³ = 1 ° С . В этом случае соответственно будет т _ВКЛ = 0,08954 х Т_В ; т _ВКЛ = 0,14299 х Т_В ; т _ВКЛ = 0,35646 х Т_В . Период следования импульсов при этом должен быть со-

ответственно таким: T_СЛЕ д = 0,216 х Т В ; Т след = 0,2699 х Т в ; Т след = 0,4861 ^х T b , ^пР^и этом скважность импульсов соответственно равна Y = 0,4145; y = 0,5296; y = 0,7333.

Далее, необходимо отметить, что под TВ сле- дует понимать постоянную времени нагрева или охлаждения собственно самого воздуха, которая, как это известно [9, 10, 13], значительно меньше, чем постоянная времени, так называемой второй стадии, когда скорость изменения температуры воздуха становится равной скорости изменения средней температуры внутренних ограждений и предметов в помещениях. В соответствии с данными работ [9, 10, 13] эта постоянная времени TВ составляет порядка нескольких часов. Поэтому период следования импульсов будет составлять от долей часа до нескольких часов, что вполне приемлемо с точки зрения режима работы коммутационного оборудования и гидравлического режима системы отопления.

Кроме того, как это известно [13–15], колебания температуры воздуха около своего оптимального значения с амплитудой в 2 ^ 3 °С в жилых и обще- ственных зданиях оказываюет благоприятное воздействие на самочувствие людей, что тоже указывает на целесообразность предлагаемого решения.

Также можно отметить, что полученное соотношение для определения периода следования им- пульсов, как это нетрудно видеть, качественно и количественно близко к результатам работы [8]. Покажем, что это действительно так. В принятых обозначениях конечная формула работы [8] имеет вид

^Т СЛЕД =

2 А З

Y (1 -Y ) ■ dt_B(0)/d T .

При этом в работе [8] полагается, что при т = 0 tB = tH, поэтому из уравнения (9) следует, что d^0) = (tMAX - 1и)/Тв,              (18)

d т если дополнительно учесть, что

1 -Y = 1 — (t B — t H )/(t MAX — t H ) =

= (t MAX - t B )/(t MAX - t H ),           (19)

то формула (17) (формула работы [8]) – перепи- шется в следующем виде:

T = T

СЛЕД В

2 А З

X-------------

,zf МАХ

Y ^(t B ^- t B )

Вместе с тем если в формуле (12) логарифм разложить в ряд и взять только первый член ряда, то полученная в данной работе формула (14) приближенно запишется так:

2 А З

T = T

СЛЕД В

x-----------------

МАХ ,З ,_лЗч Y ^(t B ^- 1 b +^A )

Как видно из (20) и (21), формулы достаточно близки, можно считать, что они практически совпадают. К месту заметим также, что в процессе вывода формулы работы [8] использовались некоторые приближенные соотношения, а при выводе формулы (12), как это следует из вышеизложенного, нет, поэтому предпочтительно для настройки импульсного погодного компенсатора использовать результаты данной работы.

Выводы

Разработан способ настройки алгоритма импульсного управления температурным режимом здания с избыточной мощностью системы отопления. Приводятся формулы для вычисления скважности и периода управляющих импульсов. Результаты работы могут быть использованы при создании систем автоматизации отоплением зданий.