Natural Image Super Resolution through Modified Adaptive Bilinear Interpolation Combined with Contra Harmonic Mean and Adaptive Median Filter

Published Online February 2016 in MECS

The super resolution (SR) is a promising digital image processing technique to enhance the resolution of an input image. The single low resolution (SLR) and multiple low resolution (MLR) techniques have been proposed to enhance resolution of input image. The high resolution (HR) image is reconstructed either from SLR [4-6][8-10][12-14][16-21][23-30] or MLR [7][10][26] of same scene with exposed from different angles. These techniques are explored in both spatial [2-4][9] and frequency [8] domain.

The remaining sections of this paper is as follows: section 2 includes the related works on enhancing resolution and restoration of an image. The section 3 explains proposed architecture with protocol phases (Interpolation and Restoration) and algorithm. The results have been discussed in the section 4 with root mean squared error (RMSE), mean squared error (MSE) and peak signal to noise ratio (PSNR) computation result statistics and finally we have summarized and concluded the paper in the section 5.

• II.    Related Work

Major research work on SR is primarily focused on building dictionary/ knowledgebase in learning and training based SR. The [2] used learning based SR which uses adaptable k neighbours for MMSE image interpolation, where in [8] used a SLR input image and a constructed knowledgebase of LR to HR pieces using discrete wavelet transform(DWT) with inhomogeneous gaussian markov random field prior. In image hallucination [16] primal sketch priors were constructed for enhancing quality of image, a contour smoothness and reconstructive constraint is applied for construction of HR image. In patch based SR, the input LR image is divided into 3X3 patches [18] then interpolated by bicubic interpolation algorithm and matched with dictionary of patches, which hold HR image patch details for interpolated LR patch. In kernel based regression [19], the pairs of input LR to output HR example pair of input and output image were trained, training piece pair are arbitrarily selected for regression from a set of LR and corresponding desired HR image.

The sparse representation [20] for SR is based on piece wise construction, where each piece of LR input is constructed and the coefficients are used to produce HR image output by together training two databases one for LR image and other for HR image pieces. In nonnegative neighbour embedding [21] a dictionary of LR and HR trained piece group are used to understand the unknown HR details where LR feature vector in the input image is weighted group of k nearest neighbours in knowledgebase and respective HR feature vector is reconstructed. In the stastical learning [23] of SR problem with support vector machine given N X N piece from LR work is to predict 4 pixels of HR image corresponding to one center pixel. Edge focused patch based hallucination [27] is an energy function framework for finding the pieces for training set/ dictionary. When a part of input is HR in LR image [28] then SR can be constructed based on gerchberg papoulis with dynamic properties.

Most of the research of SR is on building training database, some algorithms explore on reconstruction methods for construction of HR image. In developing HR image in spatial and wavelet domain [4] the input image is interpolated using bicubic then subjected to gaussian and back projection. The back projection is one of the most striking approach for generating HR image. The adaptive gradient magnitude self-interpolation [9] uses HR gradient calculation followed by reconstruction to generate HR image. As the iterative back projection produces jaggy effects [17], bilateral filtering with mean shift segmentation with complex shock filtering is used for generating HR image.

The recent SR technology uses wavelet transformations. The several wavelet transformation techniques has been applied to image processing to address interpolation for better edge enhancement to avoid blocking and jazzy artifacts. The interpolation based direction adaptive discrete wavelet transform (DWT) technology is used in image compression to reduce bit and scanning redundancy [31] for texture image which reduce computation cost for shrinking and reducing blocking artifacts with better effect along the edges. One of the major variation in DWT technology is the complex wavelet transform(CWT). The CWT technology uses two filter banks namely real and imaginary filter bank, so it is termed as dual tree complex wavelet transform. The CWT provides better directional selectivity compared to DWT as it decompose input image into eight sub bands out of which two are low frequency bands and six are high frequency bands. CWT with bicubic interpolation is used in image resolution enhancement of satellite images [32] and quick bird image data [33]. Other major variation in DWT technology is the stationary wavelet transform(SWT). The DWT mechanism will decompose the inputted image into four subcomponents with their size half of the input image causing loosing details along edges. The SWT will address this issue by having subcomponents with the same size as input image. The [34] is a combination of DWT and SWT technology as SWT components are fused with DWT components for edge enhancement. The [35] is a hybrid algorithm based on DWT technology and spatial domain gaussian filtering and back propagation for image resolution enhancement.

In HR image building the input LR image is to be interpolated and for that most familiar are the variations of bicubic interpolation mechanism, which uses 16 nearby pixels for generating new values for interpolated pixel. When we use bicubic the value of interpolated pixel is dependent on 16 surrounding pixel so it introduce error between actual original image and the interpolated image along edges. To reduce error we are proposing a new approach of interpolation termed MABI which uses only seven surrounding pixels. By applying MABI error between actual original image and the interpolated image are reduced and the interpolated image is then subjected to restoration for HR image reconstruction.

• III.    Proposed Architecture

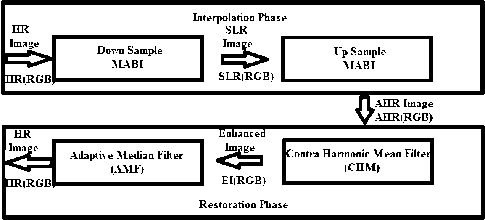
Fig.1. Proposed SR Architecture

The proposed SR architecture as shown in figure 1 accepts HR Image as input, which is also used as a reference for comparing the quality of approximated HR (AHR) image. SLR image is generated by down sampling HR image using proposed MABI interpolation function shown in figure 3 as per architecture shown in figure 4.

• A.    Notation

Table 1 briefs the notations used in this article for proposed SR architecture.

Table 1.Notations used in proposed architecture

Notation	Explanation
SLR(RGB)	Single low resolution colour (Red, Green, Blue) image.
IP(RGB)	Input colour image.
OP(RGB)	Output colour image.
AHR(RGB)	Approximated high resolution colour image.
EI(RGB)	Enhanced high resolution colour image.
HR(RGB)	High resolution colour image.

• B.    Interpolation Phase

Figure 2 depicts the protocol used in interpolation phase for the proposed architecture shown in figure 1.

The interpolation phase starts from accepting SLR(RGB) image from the user. The SLR(RGB) is interpolated by a factor of ∂ using proposed MABI function and AHR(RGB) is generated. The result of interpolation phase is subjected to restoration phase shown in figure 5.

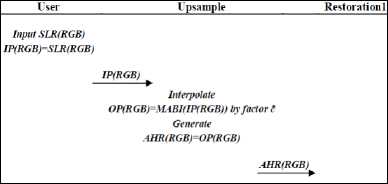
Fig.2. Protocol used in Interpolation phase

Function МАВЩРMx^RGBPOPgMxgNfRGB))

// IPmxn(RGB) input image of size product (M.N.3)

// OPsmxsn(RGB) interpolated image of size

// product (6M, dN,3) with an interpolation factor 8. begin for i = 1 to 8*M step 1

forj = 1 to 8*N step 1

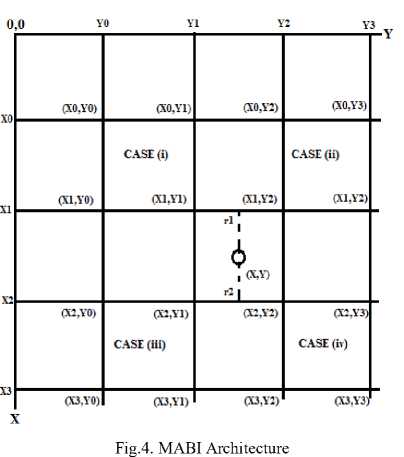
//Map interpolated pixel with (if) co ordinates to input // image (x, y) co ordinates

//Apply bilinear interpolation on input image pixel

//values, Г] represent interpolation along X] axis and //r2 represent interpolation along x2 axis of figure 4 //and final result in stored in Result! x>y(RGB)

>1 = IPx^RGB) + f * (IP_Xvy2(RGB) - 1P_{X y} (RGB)) ¹¹      ЧУ2-У1У ^{12        11}

! (y "" У1) \

(x - Xj) ' (x2 -xt)

Resultl_xy(RGB) = r,

//Alter any one of the surrounding pixel values based on

x0=xrl; Уо=У1-1; x3=x2+l;   y3=y,+l:

if(x=X] andy^fi

Lp^q^.ilPx^RGB) ipXvy2(RGB) =        9 4     ----- if(x=x2 andy=y,)

Sp=2,3 Sq=O,l P(y (.RGB) lPX2yfRGB) =  ----9 4    ----- if(x=x2 andy=y2)

5р=2,з5д=2,3 lPx_.y„(RGB) lP_X2,y₂(RGB) =        ⁹₄     ------

//Apply bilinear interpolation on altered surrounding //pixel values and store result in Result2xy(RGB)

/ (y - yi) \ ri = IPX1,yfRGB) + I-------- * UPxvyfRGB) - lPXiiyfRGB)) ЧУ2 -

Ч = !Px„yfRGB) +          * (1PX1№(RGB) - lPXl.,fRGB))

Result2_xy(RGB) = r₂ +              (r₂ - г_х)

//Fuse the results with max filter and store at //interpolated pixel (if) co ordinates of output image OPij^RGB) = maxQResultlxy^RGByResuLt^x yt^RGB')') end for end for end

Fig.3. Function MABI

The image interpolation function ranging from nearest neighbor to bicubic suffers from blurring edges and loosing image details, So in order to improve interpolation mechanism MABI is proposed. The figure 3 shows the implementation details for MABI architecture shown in figure 4, which not only interpolates the input image but also increases smoothness using smoothing kernel.

• C.    Restoration Phase

Figure 5 shows the protocol used in restoration phase for the proposed architecture shown in figure 1. The restoration phase is done in two levels restoration 1 and restoration 2. Restoration 1 accepts AHR(RGB) generated from interpolation phase shown in figure 2 and uses CHM filter, which reduces jaggy effect in generated AHR(RGB) using a smoothing kernel of order Q. The result of restoration1 is EI(RGB) is feed into restoration 2 level. The restoration 2 uses AMF to generate HR(RGB). AMF is a local filter works based on non linear median filtering, which produces better results [1] than other linear filtering mechanisms. The generated HR(RGB) is visually pleasant HR image generated from SLR image using SR mechanism.

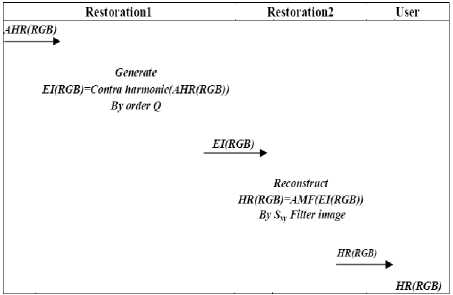
Fig.5. Protocol used in restoration phase

The AHR(RGB) image of MABI is subjected to CHM kernel [1][4] as shown in equation (1), which is used as smoothing kernel in spatial domain.

_ Lu₀₆$„AHR(RGBHst^

( "^7оё7^анй(нсв57Т^ (1)

Where

AHR(RGB)-> MABI interpolated RGB image.

Q -> Order of the filter.

EI(RGB)->Enhanced RGB image obtained after contra harmonic mean filtering.

The EI(RGB) image is subjected to AMF [1] algorithm shown in figure 6. AMF is a non linear filter to significantly reduce irregularities in generated image and sharpen the EI(RGB) image which is termed as SR image.

Algorithm AMF(EI∂MX∂N(RGB),OP∂MX∂N(RGB)) // EI∂MX∂N(RGB) input image of size product(∂M, ∂N,3)

// SR∂MX∂N(RGB) SR image of size product(∂M, ∂N,3).

begin

Stage A:

Value1= EI(RGB) med - EI(RGB) min

Value2= EI(RGB) med - EI(RGB) max

If(Value1 > 0 ) and (Value2 < 0 ) go to stage B Else increase the window size

If window size ≤ S max repeat Stage A

Else output SR(RGB)=EI(RGB) med

Stage B:

Value3 = EI(RGB) xy - EI(RGB) min

Value4 = EI(RGB) xy - EI(RGB) max

If (Value3 > 0 ) and (Value4 < 0 ), output SR(RGB)=EI(RGB)xy

Else output SR(RGB)=EI(RGB) med end

Where

EI(RGB) min : Minimum intensity value of S xy EI(RGB)_max: Maximum intensity value of S_xy EI(RGB)_med: Median intensity value S_xy EI(RGB)_xy :Intensity values at coordinates (x,y) S_xy: Filter image

S max : Maximum allowed size of S xy

Fig.6. Algorithm for adaptive median filter

• IV.    Results and Discussion

The first part of our SR algorithm involves interpolation. The set of input images shown in figure 7 are considered for experimentation on proposed MABI, nearest neighbor, bilinear and bicubic interpolation in MATLAB. The input images are referred from standard MATLAB data set.

(i) Lena Size:256X256X3

The obtained results for figure 7 case (i) input image are shown in figure 8 and are compared with original image using RMSE, MSE and PSNR and tabulated in table 2. There is drastic decrease in RMSE, MSE and significant increase in PSNR. Which shows that our method of interpolation MABI calculate near to original image better than other techniques and competent to result of learning/training based SR algorithms.

(ii): Lena Size: 512X512X3

(a) Nearest neighbor

(b)Bilinear

Size: 486X732X3

(c)Bicubic

Fig.7. Set of input images

(d) MABI

Fig.8. Interpolation of input image(i) from figure 7.

Table 2. RMSE, MSE and PSNR Computation statistics

Image	RMSE Tabulation
	Nearest Neighbor	Bilinear	Bicubic	MABI
Lena 256X256X3	5.2128	4.8560	4.4997	3.5684
Lena 512X512X3	4.9409	4.3062	4.1357	3.3934
onion.png 135X198X3	4.9053	4.5358	4.2778	3.2784
pears.png 486X732X3	3.7416	2.9790	2.8964	2.2744
west.png 394X369X3	6.4076	6.0621	5.4526	4.4604
Image	MSE Tabulation
	Nearest Neighbor	Bilinear	Bicubic	MABI
Lena 256X256X3	27.1740	23.5810	20.2475	12.7337
Lena 512X512X3	24.4127	18.5439	17.1043	11.5153
onion.png 135X198X3	24.0626	20.5733	18.2995	10.7482
pears.png 486X732X3	13.9997	8.8744	8.3893	5.1730
west.png 394X369X3	41.0571	36.7493	29.7307	19.8952
Image	PSNR Tabulation
	Nearest Neighbor	Bilinear	Bicubic	MABI
Lena 256X256X3	33.7893	34.4052	35.0671	37.0813
Lena 512X512X3	34.2546	35.4488	35.7997	37.5180
onion.png 135X198X3	34.3174	34.9978	35.5064	37.8174
pears.png 486X732X3	36.6696	38.6494	38.8935	40.9934
west.png 394X369X3	31.9969	32.4783	33.3988	35.1433

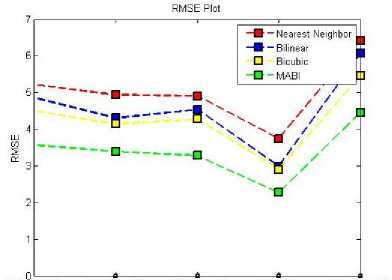
Fig 7 case(i) Fig 7 case(ii) Fig 7 case(iii) Fig 7 case(iv) Fig7case(v) Figure

Fig.9. RMSE Performance of different interpolation methods for SR evaluated as per table 2 RMSE tabulation cost

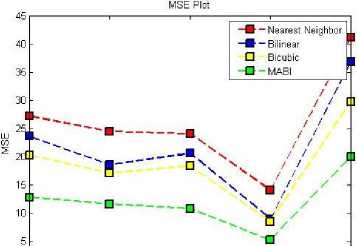
Fig 7 case(i) Fig 7 case(ii) Fig 7 case(iii) Fig 7 case(iv) Fig 7 case(v) Figure

Fig.10. MSE Performance of different interpolation methods for SR evaluated as per table 2 MSE tabulation cost

The RMSE performance of figure 9 and MSE performance of figure 10 reveals designed MABI function approximates SLR to approximated HR, which very closely resembles original HR. The error rate between state of art algorithm is very less.

PSNR Plot

О — Nearest Neighbor

—- Bilinear

□ Bicubic

□ MABI

Fig 7 case(i) Fig 7 case(ii) Fig 7 case(iii) Fig7case(iv) Fig7case(v) Figure

Fig.11. PSNR Performance of different interpolation methods for SR evaluated as per table 2 MSE tabulation cost measured in dB

The analysis of figure 11 PSNR performance shows approximated signal rate is high than noise compared to other interpolation algorithms. The study of figure 9, 10 and 11 shows MABI interpolates more accurately than other interpolation techniques for super resolution in SLR interpolation domain.

The CHM kernel is applied on proposed MABI resultant image obtained in figure 8 (d) for increasing psycho visual effect. The result of CHM is sharpened using AMF to remove blurriness and introduce smoothness at edge transitions as shown in figure 12.

Fig.12. Reconstruction from the interpolated image

• V.    Conclusion

In this paper, we have designed and implemented MABI algorithm and tested on several color images. The obtained results are compared with the current interpolation algorithms in spatial domain for single color image SR. The proposed algorithm is useful for creating HR colour image. The study of this algorithm put conclusion that interpolation algorithms in spatial domain will not exactly approximate along edges. Restoration mechanisms are needed for increasing accuracy on edges, which is done using CHM and AMF mechanisms. Competitive result statistics shows the potential of our MABI algorithm.