Наведение и гиросиловое управление ориентацией спутника землеобзора при сканирующей стереоскопической съемке

Современные спутники землеобзора обладают возможностью стереоскопической съемки высокого разрешения на местности в плане и по высоте с одного витка орбиты путем отклонения оси визирования одного объектива относительно надира либо используя два объектива, закрепленные в корпусе космического аппарата (КА) под фиксированными углами. Такой тип стереосъемки называют конвергентным, он характеризуется углом конвергенции двух изображений местности – стереопары, полученной в результате выполнения сканирующей съемки местности с двух ракурсов.

Рассматривается КА землеобзора, оснащенный телескопом с матрицами оптико-электронных преобразователей (ОЭП) в его фокальной плоскости (ФП). При съемке участков поверхности Земли совокупностью маршрутов их сканирования телескопом матрицы ОЭП работают в режиме временной задержки и накопления (ВЗН). На поверхности Земли маршрут съемки отображается следом проекций ОЭП, составляя полосу захвата. При известном орбитальном движении центра масс (ЦМ) спутника маршрут съемки определяется законом углового наве-

фундаментальных исследований № 13).

дения КА, при котором происходит требуемое движение оптического изображения по фотоприемной поверхности ОЭП.

С применением известных приемов космической геодезии [1-6] авторами разработаны аналитические методы синтеза законов наведения КА при произвольном виде сканирующей съемки, которые основанные на методах анализа векторного поля скоростей движения изображения (СДИ) наземных объектов на матрицах ОЭП с ВЗН. Созданные методы конкретизированы для трассовых, протяженных криволинейных маршрутов с выравниванием продольной СДИ, объектовой съемки – короткого маршрута с оптимальным начальным геодезическим азимутом [7-11], для площадного землеобзора [12] с последовательностью ортодромических маршрутов, а также для получения стереоизображений выбранных участков на поверхности Земли.

На последовательности чередования маршрутов сканирующей стереосъемки и быстрых поворотных маневров (ПМ) спутника с краевыми условиями общего вида управление ориентацией КА выполняется силовым гироскопическим кластером (СГК) на основе четырех гиродинов (ГД) по сигналам бесплатформенной инерциальной навигационной системы (БИНС) с астрономической коррекцией. При формировании стереопары имеется ряд требований к динамическим характеристикам системы управления ориентацией (СУО) в процессе ПМ спутника между двумя маршрутами съемки заданной местности с двух ракурсов. Эти требова- ния связаны с ограниченными ресурсами СГК по допустимой области вариации вектора его кинетического момента (КМ), а также по допустимым скоростям и ускорениям угловых перемещений ГД.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Используются стандартные системы координат (СК) - инерциальная (ИСК O _e X e Y eI Z ; , базис I _ф ) с началом в центре Земли O _ф ; связанная с вращающейся Землей геодезическая Гринвичская (ГСК O _ф X^eY^eZ^e , базис E ); гори-зонтная (ГорСК CX^hY_c^hZ^h , базис H _c ) с эллипсоидальными геодезическими координатами L_c,B _c, H _c , началом в точке C с высотой H _c по орту внешней нормали n ^e к поверхности общеземного эллипсоида (рис. 1); орбитальная (ОСК O x ⁰ y ^o z ⁰ , базис O с ортами радиали r ⁰ , трансверсали т ⁰ и бинормали n ⁰ ) и связанная с КА (ССК O xyz , базис B ) системы координат с началом в его центре масс O (рис. 2). Вводятся телескопная СК (ТСК, базис S с ортами s i , i = 1,2,3 = 1 ^ 3 ) с началом в центре оптического проектирования S (см. рис. 2), СК поля изображения O x i y iz^l с началом в центре O i ФП телескопа (рис. 3) и визирная система координат (ВСК O_v x ^v y ^v z ^v , базис V с ортами v i ), связанная с матрицей ОЭП, см. рис. 3. Орт s 1 телескопного (оптического) базиса S = { s i } ориентирован вдоль оптической оси телескопа S X^s , а орты S ₂ и S 3 направлены по осям S y ^s и S z^s соответственно, см. рис. 2. Далее применяются стандартные обозначения для векторов ^col0 = ^{} , lineQ = [ • ] , (,), матриц [ • ] i , ( - ) ‘ , [ a x ] и кватернионов о ,~ .

Угловое положение ГСК относительно ИСК определяется углом ^р e ^{( 1} ) = ^{р 0} + ^_е ⁽ t ^- t ₀) ,

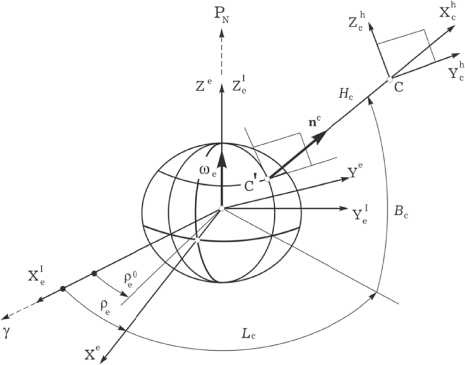
Рис. 1. Базисы Iф, E и H см рис. 1, где р0 = pe(10) - угловое положение Гринвичского меридиана при 1 = 10 относительно направления на точку Весны Y, а Юе = | Фе | = | Юф | - угловая скорость вращения Земли. Поверхность Земли описывается в виде сжатого в направлении ее полюсов эллипсоида вращения с полуосями ae, ce и коэффициентом полярного сжатия a p = 1 - (ce I ae). Преобразование эллипсоидальных геодезических координат Bc, Lc, Hc в декартовые геодезические координаты Xc,Yce, Zc выполняется по соотношениям

xc = (Nc+Hc) Cb.Cl .;

Y = ( N. + Hc) C.SlJ z; = (1 - e 2) N. + H,) S,c, где использованы обозначения Sa = sin a , C = cos a и Nc = ae /(1 - eS )1/2 - радиус кри-αc визны первого вертикала, ep = J1 -(1 -ap)2 -

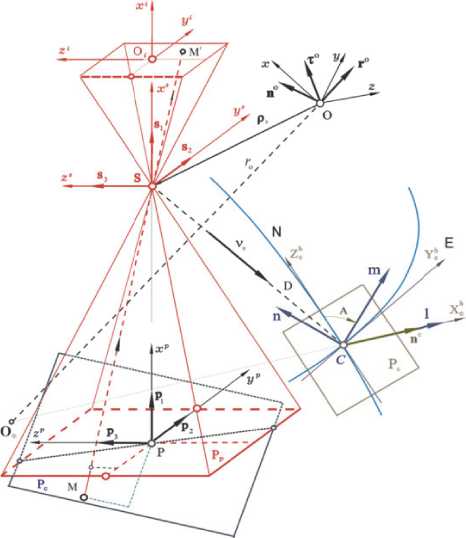
Рис. 2. Геометрия сканирующей съемки

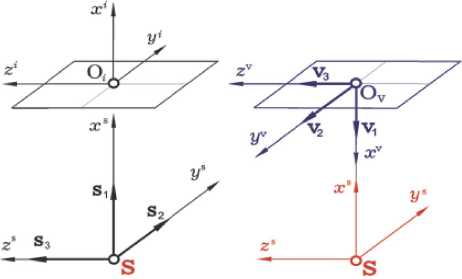
Рис. 3. СК поля изображения и базис V

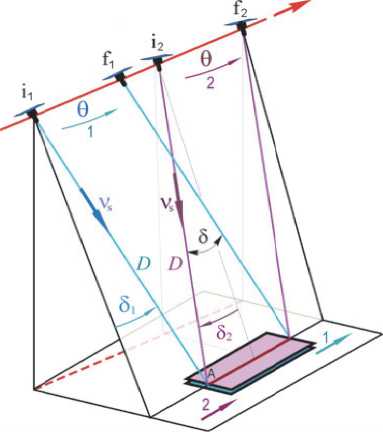
Рис. 4. Схема выполнения стереосъемки

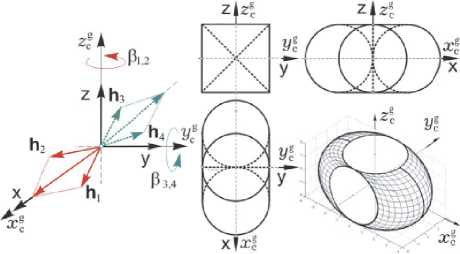
Рис. 5. Схема СГК и область вариации его КМ

эллипсоидальными координатами B _c , L _c , H _c наиболее просто определяется в ГорСК H _c . При известном угловом положении связанного базиса B относительно ИСК, определяемом матрицей C _I ^b или соответствующим кватернионом, ради-

эксцентриситет меридианного эллипса земного эллипсоида. Обратное преобразование выполняется по формулам

Bc = arctg[(Zc + aeeppS3c /(1 -ap))/(r/ -aecpC3c)];

Lc = arctg(Y:/XC); Hc = (Xc/(CBc Cl c)) - Nc;

= Yec /( Cbc Slc) - Nc = (Zc / Sbc) - (1 - e pp)/ Nc

при обозначениях tg 0 _c = Z _c^e(l -a _p ) ^l/ r_c^p и Г = j (X^ + (Y c' )^p .

При столбцах M ‘ = {X m ,Y m ,Z m } и C ^e = {X C ,Y_c^e,Z C } , составленных из координат произвольных точек M и C в базисе E соответственно, столбец M ^h = {X ^^ Y ^^^ } , составленный из координат точки M в ба-

зисе H _c , вычисляется по соотношению М ^h = T _e^h( B _c, L _c)( M ^e - C ^e) , где матрица T eh с определителем det( T _e^h) = 1 ортогонального преобразования координат при переходе от ба-

зиса E (нижний индекс «e») к базису H _c (верхний индекс «h») имеет вид

C B c C L c

C B c S L c

h e

S

L _c

C

L _c

S B c

0

^^^^^^^s

S B c C L c

^^^^^^^s

S B c C L c

C B c

Имеются также явные аналитические соотношения для вычисления горизонтных геодезических координат X^h_m ,Y_m^h , Z^h_m точки M , как функций только эллипсоидальных координат B _m, L _m, H _m и B _c, L _c, H _c точек M и C соответственно.

Орт v s целеуказания из фиксированной в ССК точки S на произвольно заданный объект C в окрестности точки С ’ на поверхности эталонного земного эллипсоида с геодезическими

ус-вектор rs (t) точки S c ортом rs (t) в инерциальном базисе становится также известным. При обозначении столбца SI = {XS,YsI,ZS} координат точки S в ИСК столбец se = {Xe, Yse, Ze} прямоугольных геодезических координат этой же точки в базисе E получается простейшим ортогональным преобразованием координат: Se = [Pe(t)]3 S1. Точка C является началом базиса Hc, в этом базисе орт целеуказания vs представляется вектором-столбцом V^ = {v^} и вычисляется по явной формуле vh = sh / sh , h   hhh где s =-{Xs, Ys ,Zs}. Гарантирующее условие «прямой видимости» произвольной точки C, расположенной в окрестности точки С’ на поверхности Земли, из произвольной точки S на борту КА, ЦМ O которого находится в произвольной точке его известной орбиты, состоит в проверке лишь одного неравенства Xh > 0.

Высота полета КА над земным эллипсоидом, мгновенное положение на нем подспутниковой точки с геодезическими координатами и трасса спутника, как след положений точки О ’ на поверхности Земли, получаются расчетом эллипсоидальных геодезических координат B _o , L _o , H _o по известным компонентам столбца r oe = {X 0 ,Y o ^e,Z 0 } в базисе E . Далее для компактности представления метода синтеза законов наведения КА точка S совмещается с точкой O, что достигается при p b = 0 и приводит к тождеству r _s ^e = r _o ^e , хотя на рис. 2 точки O и S намеренно разнесены.

Наряду с матрицей C _I ^b ориентация ССК в ИСК определяется кватернионом Л b = Л = ( X 0 , Х ) , Х = { X i } . Применяются векторы угловой скорости ю и углового ускорения е , а углы ориентации ССК относительно ОСК по крену ф 1 = у , рысканию ф ₂ = V и тан-

гажу ф ₃ — 0 используются в последовательности 312 для формирования матрицы С ^ . Далее применяется вектор модифицированных параметров Родрига (МПР) о = { о i } = е tg( O /4) с традиционными обозначениями орта оси Эйлера e и угла Ф собственного поворота. Вектор О взаимно-однозначно связан с кватернионом Л прямыми о = X / (1 + Х ₀) и обратными Х _о = (1 — о ²)/(1 + о ²) , Х = 2 о /(1 + о ²) соотношениями.

Кинематическое уравнение для кватерниона Л ориентации ССК относительно ИСК имеет вид

Л = Л о ®/2,               (1)

для вектора МПР О прямые и обратные кинематические соотношения представляются как о = 1(1 — о ²) ® + 1 о х ® + 1 о(о , ® ;

® = 4[(1 — о 2)о — 2(охо)             (2)

+ 2о^о, о )]/(1 + о2)2, его вторая производная

о = у [—о, о)® + 1(1 — о2)8 + о х®+ о X 8 + о(о, ®) + о^о, ®) + о^о, 8)].

Кватернион Л ^ ориентации телескопа в ГСК, столбцы ® ^ и v e проекций векторов угловой и поступательной скоростей ТСК на оси базиса S — { s i } в базисе E определяются соотношениями

л:=л^ о ль о ль; л:=л: о ®s/2;

®s = К(® — СЬ®ф); vs =Л^ о V: о Лs,

где вектор угловой скорости to = to b , матрица T bs учитывает угловую фиксацию телескопа в корпусе КА и столбец v 0 представляет вектор скорости поступательного орбитального движения ЦМ спутника в ГСК. Представленные соотношения полностью определяют пространственное положение, вектор скорости поступательного движения центра S проектирования (совмещенного с точкой O) и вектор скорости углового движения телескопа относительно геодезического гринвичского базисе E в проекциях на оси оптического базиса S .

На рис. 4 приведена упрощенная схема стереосъемки, которая содержит два маршрута сканирования заданного участка земной поверхности, где для иллюстрации идеи эта поверхность считается неподвижной плоскостью. Здесь красной прямой линией отмечена орбита спутника с начальными (initial) i j и конечными (final) f j точками первого (j — 1, голубой цвет) и второго (j — 2, бордовый цвет) маршрутов, красная пунктирная прямая линия представляет след орбиты. Если для наглядности описания стереосъемки с углом конвергенции 6 использовать стандартные понятия для направлений векторов в ОСК, то каждый маршрут сканирования начинается в фиксированной точке A ГСК, заданной с назначенным превышением относительно поверхности общеземного эллипсоида. При этом в момент времени ti1 начала первого маршрута с дальностью D наблюдения точки A орт целеуказания v s получается отклонением от надира сначала по крену и затем по тангажу на угол 61 — 6/2. Первый маршрут должен выполняться с условиями D — const , 61— const Vt g [t;(1), tf1) ] за счет углового наведения КА в ОСК по углу тангажа 0, см. рис. 4, голубой цвет. Далее следует поворотный маневр КА на интервале времени t g [tf1), ti(2)]. В момент времени ti начала второго маршрута с той же дальностью D наблюдения указанной точки A ГСК орт целеуказания vs формируется отклонением от надира, достигнутого при t — t;(2), по крену и тангажу на угол 62 — -6/2, этот маршрут должен выполняться с условиями D — const,62 — const Vt g [ti(2),tf2)] также за счет углового наведения КА в ОСК по углу тангажа 0, см. рис. 4, бордовый цвет.

Первая задача состоит в синтезе закона наведения КА для получения стереопары изображений участка на поверхности Земли при выполнении двух маршрутов его сканирования с требуемыми условиями D — const, 6j — const, j — 1,2, и соответствующими продольной и поперечной СДИ в центре матрицы ОЭП, а также для выполнения быстрого поворотного маневра спутника между этими маршрутами с рассчитанными краевыми условиями.

Если считать, что упругие панели солнечных батарей (СБ) жестко фиксированы на корпусе спутника с тензором инерции J , то модель динамики углового движения КА имеет вид

D t A q q ^q J I— •

F ^to

.

F ^q

Здесь столбцы F ^m—- to x ( D _q q + G °) + M ^g + M ^d и F ^q —- A ^q ( V _q q + W_q q ) ; вектор G ^o — J to + H , где столбец H — { H i } представляет вектор КМ СГК; D _q – матрица взаимовлияния вращательного движения КА с упругими перемещениями панелей СБ; A⁴ , V и W _q - диагональные матрицы нормированных масс, демпфирования и жесткости конструкции КА; M ^g - вектор управляющего момента СГК и вектор M ^d представляет внешние возмущающие моменты.

Для управления ориентацией КА применяется СГК на основе четырех ГД. На рис. 5 представлена каноническая схема 2-SPE (система 2 ножничных пар – 2 Scissored Pair Ensemble), состоящая из двух пар ГД с ортами КМ hp (вp), p = 1 ^ 4, область S вариации нормированного вектора КМ такого кластера h(P) = Lhp (вp) , где столбец р = {Рp} , и ее проекции на плоскости симметрии гироскопической СК Oxgygzg . Вектор КМ СГК имеет вид H = hgh(P), где hg – одинаковое для всех ГД постоянное значение модуля собственного КМ. Вектор управляющего момента СГК Mg формируется в виде Mg = -H* =-hgAh(P) ug, P = ug = {up}, где (•) - символ локальной производной по времени и матрица Ah (р) = dh(P)d P. При цифровом управлении uk(t) = {upk (t)} с периодом Tu и столбцом дискретных команд uk = {upk} формируются   кусочно-постоянные   функ ции upf (t) = upf Vt E[tk , tk+1) , tk+1 = tk + Tu , k E N0 = [0,1,2,...) управления ГД и в результате СГК создает вектор управляющего гироскопического момента ■

M k ( t ) = - h g A h ( P ( t ) u k ( t ) ; P ( t ) = u g ( t ) . (6)

Измерение углового положения и угловой скорости КА в ИСК (кватерниона Л и вектора го ) выполняется БИНС [13] в моменты времени t_l , l E N₀ , с периодом T q , кратном периоду управления T_u . Пусть известен закон наведения спутника землеобзора Л ^p ( t ), Ю ^p ( t ),( b ^p ( t ) = £ ^p ( t ) в ИСК для выполнения маршрутов сканирующей стереосъемки и поворотных маневров КА между ними. Вторая задача состоит в синтезе закона цифрового управления СГК, обеспечивающего прецизионную стабилизацию углового движения КА при реализации рассчитанных законов наведения при сканирующей стереосъемке.

ЗАКОНЫ УГЛОВОГО НАВЕДЕНИЯ

Наряду с СК поля изображений (O i x¹ , y i , z¹ ) и ТСК (S X^s y^s z ) на рис. 2 вводятся

• •    ортогональная СК пространства предметов наблюдения CX ^ Y _c ^h Z ^ с началом в точке C - «предметный» базис P c = { p c } с ортами Р 1 , ^p 2 и ^p 3 по осям X h , Y_c^h и Z h соответственно, c основной «предметной» плоскостью

Р_с = (Y c ^hCZ h );

• •    ортогональная СК поля видимых предме-

• тов (Pxpypzp) с началом в точке P и основ

ной плоскостью Pp = (ypPzp ) - «картинный» базис Pp = {pi}, причем соответствующие орты базисов S и Pp взаимно параллельны и точка P принадлежит основной «предметной» плоскости P„

• c _.

Пусть в плоскости Pc задан орт m с произвольным геодезическим азимутом A E [-п, п] , который классически отсчитывается от северного направления касательной к местному меридиану по часовой стрелке. Определим орт l = nc, ортогональный «предметной» плоскости Pc базиса Pc, и орт n = l х m, принадлежащий плоскости Pc, см. рис. 2. Для удобства будем считать A E [0, 2п] и введем угол BA = п /2 - A, дополняющий азимут A до п /2 , причем отсчет угла BA выполняется от восточного направления касательной к местной параллели стандартно – против часовой стрелки при взгляде с конца орта l . Маршрутный базис P™ определяется в горизонтном геодезическом базисе Hc тремя ортами l, m, n на основе соотношения P™ = {l, m, n} = [BA ]1 Pc , поэтому представления ортов m и n в базисе Hc получаются в виде m = CB p2 + SB p 3 и n = -SBA p 2 + CBA pc.    Общеизвестные тождества    CB^ = cos(K /2 - A) = -SA    и

SB^ = sin( п / 2 - A ) = C_A позволяют представить полученные соотношения в явной зависимости от геодезического азимута A . Векторы-столбцы l e , m С и n С из проекций ортов l , m , n в геодезическом базисе E вычисляются по соотношению x e = T _h^e( B _c, L _c) x h , x = l , m , n , где матрица T _h ^e = ( T _e ^h ) t . В итоге орт целеуказания v _s , = D / D , где вектор наклонной дальности D = r _p - r _o точки P по линии визирования из точки O , вычисляется по аналитическим соотношениям как в гринвичском базисе E , так и в горизонтном базисе H _c .

Введем текущий «картинный» базис P p = { p 2 } и текущую «картинную» плоскость P ^ , проходящую через точку P (которая совпадает с точкой C ) и ортогональную орту S 1 = p { = - v _s . Последнее условие выражается соотношением ^p { , a ₂ ^ = 0 , где a ₂ - произвольный вектор, принадлежащий плоскости P p . Задача назначения ортов p 2 и p 3 в плоскости P ^vv из условия совпадения направлений орта p 2 и проекции m 2 орта m на плоскость P p с определением требуемого положения всех трех ортов s _i базиса S имеет аналитическое решение

_       __V - . . _       __V __V . ___ V .

• ^s 1 = p 1 = ^-v s ; ^s 2 = p 2 = p з ^х p 1 ;

S 3 = p ² = ( p v х m )/| p v х m| .

Пусть «картинный» базис Pp имеет требуе-Pv p , т.е. выполнено тождество Pp = Pp. Для ортов маршрутного базиса Рст справедливы соотношения Pcm = [BA ]1 PС и pcm = qpp , где ортогональная матрица Q =|| q.. || имеет компоненты q1 j = ^l,pj^; q2 j = ^m,pv^", q3j = (n,pj^, j = 1 ^3, причем q23 = 0. Поэтому связь ортов «картинного» базиса Pp = Pp и горизонтного базиса H c = Pc = {p С} в точке C выражается как Pp = Pj = CPc, где матрица перспективы наблюдения C = Q t[BA ]1. Для определения связи координат точки M, представленной в геодезическом базисе H c = PС столбцом Mh = {X^Y^Zm}, с отображением этой же точки M в «картинном» базисе Pp в виде столбца Mp = {xp, yp, zp} необходимо учитывать совмещенность точек C и P , а также взаимное угловое положение этих базисов. В итоге получаются соотношения в виде Мp = СМh; Мh = СМp , где матрица С =|| су ||= Ch представляет перспективу наблюдения – ориентацию текущего «картинного» базиса Pp относительно базиса PС = H c.

Если не учитывать кривизну земной поверхности в малой окрестности точки C , то точке M соответствует столбец координат M ^h = ^Y^Z ^ } . Отображение точки M в точку M ' ( y¹ , z i ) основной плоскости СК поля изображений удобно выполнять непосредственно в базисе S при использовании столбца M ⁵ = { x^s , y^s , z s } координат точки M в этом базисе и столбца M ' = { y i , z i } координат точки M ' в плоскости y i O i z i , см. рис. 2. Применение соотношений центральной проекции теории оптических систем и дифференцирование их по времени с учетом подвижности базиса S

относительно ГСК при столбцах to ss = { to p i } и v C = {v C / } (6) приводит к явному соотношению

i — 5

— i

i ^y

i

z

y i ~i z

1

0

0

1

q ve1 — У

is q ve2

-

' 5 . — i , ^ 5

toe3 + z toe2

5       -—' i , 5

toe3 - z toe1

i — 5 . q v el +

„ 5 , — i , , 5

toe2 + y toe1

для вычисления вектора V1 = {Vy, Vz } нормированной СДИ с компонентами V1 (—1,—i) = —1 y и Vz1 (—1, —1) = —1 . Здесь —1 = y I fe и у1 = z1 / fe являются нормированными фокальными координатами точки M , где fe - эквивалентное фокусное расстояние телескопа, скалярная функ-

в ГСК, нормированные к дальности D , вычисляются по соотношению v P , = v ^ / 1 D , i = 1 ^ 3.

Ориентация орта m маршрутного базиса P _c ^m определяет требуемое расположение отображения столбцов матрицы ОЭП на «предметную» плоскость P _С , а ориентация ортогонального ему орта n – требуемое расположение отображения строк матрицы ОЭП на эту же плоскость. Положение точки C в ГСК с заданным превышением h над земным эллипсоидом при известном орте целеуказания V ® = { v ^C _si } определяется из уравнений r _c ^e = r _o ^e + d V 5 и е 2 е 2 е 2    2                  2

^(Х с ⁾ + ^(YJ + ⁽Z_C) / р _р = ⁽ a e + ^h) . Здесь скаляр d участвует в параметрическом представлении луча, направленного по орту целеуказания V 5 из точки S в сторону Земли, а параметр 0 ² = 1 - e ² = (1 -а )² характеризует сжатие земного эллипсоида. Совместное решение этих двух уравнений сводится к анализу уравнения ad ² + 2 bd + c = 0 относительно параметра d с коэффициентами a , b и c , которые вычисляются по явным соотношениям. В анализируемых условиях всегда коэффициент b <  0 , поэтому наименьшее значение параметра d = d * вычисляется явно. Это дает возможность получения искомых координат точки C в геодезическом базисе E и значения дальности D = d * этой точки относительно центра проектирования S, совмещенного с центром масс О спутника, по явным формулам X C = X p + Dv^e^, Y C = Y₀^C + Dv ^2 и Z C = Z P + Dv^ 3 .

Если выполняется сканирование с ВЗН и выравниванием постоянной продольной СДИ в произвольной точке (— * ,^— / ) ФП телескопа, то должны выполняться два условия: (i) компоненты вектора СДИ V_z * (—,^{— 1} ) = 0 , V y (— * ,^{— 1} ) = W y, = const ; (ii) перемещение изображения выровнено по столбцов матрицы ОЭП, д Vy (— * ,^{— 1} )/ d z¹ = 0 . Применение этих условий в универсальной формуле расчета поля скоростей (7) приводит к явному соотношению для вычисления всех трех компонентов вектора угловой скорости to C оптического базиса S относительно геодезического базиса E . Так, для маршрута сканирования с выравниванием продольной СДИ в центре (— * ,^— , ) = (0,0) матрицы ОЭП компоненты этого вектора определяются по элементарным соотношениям

X ~ X ~ ,~ X ® с1 =   ^v c2 c 31 ^/ c 11 ;    ® с2 =

toXe3 =— W + vy с               у         C Z,

~ X

—vc3;

ция q = 1 — ( c ₂₁ y + c ₃₁ z )/ c₁₁ и компоненты вектора скорости поступательного движения КА

Несмотря на небольшой недостаток (монотонное искривление маршрута на земной по-

верхности), при такой съемке получается космическая видеоинформация самого высокого качества.

При простейшей трассовой съемке с постоянной продольной СДИ в центре матрицы ОЭП, которая выполняется с фиксированным положением линии визирования телескопа в ОСК, когда ее след на земной поверхности отражается линией, эквидистантной трассе спутника. При ортодромической съемке, которая обычно применяется для площадного землеобзора также с постоянной продольной СДИ в центре матрицы ОЭП, осевые линии маршрутов соответствуют геодезическим линиям заданной высоты над земным эллипсоидом. В процессе выполнения сканирующей съемки этих видов компоненты V_y (0,0) и V (0,0) вектора СДИ в точке O . (0,0) определяются из условий

V y (0,0) = 0 ; V z (0,0) = W y , (9) вектор СДИ в этой точке перпендикулярен оси O iz¹ СК поля изображения и след оси визирования должен располагаться соответствующим образом на земном эллипсоиде.

При синтезе закона наведения КА для получения стереопары изображений заданного участка на земной поверхности в процессе выполнения маршрутов его сканирования с двумя ракурсами следует учитывать, что невозможно обеспечить строгое постоянство продольной СДИ в центре матрицы ОЭП при соблюдении основного условия D = const стереосъемки, здесь приходится изменять текущие значения азимута маршрута и продольной СДИ в центре матрицы ОЭП.

Начало A первого маршрута съемки (МС1) определяется из условия достижения значения угла 51 = 5/2 между траверсом точки A на орбитальное положение КА и ортом целеуказания V s на эту точку при заданном угле конвергенции 5. Это условие определяет также момент времени ti1 начала МС1 и дальность Di(1) наблюдения точки A . Выполняется расчет закона углового наведения КА, движущегося по известной орбите, на первом шаге малой длительности Ts по соотношениям (8) при итерационной вариации значений азимута A маршрута и продольной СДИ так, чтобы в результате выполнения такого шага дальность D наблюдения достигнутой точки на земном эллипсоиде была равна D;(1) = D. Далее описанная процедура повторяется с периодом Ts в очередной достигнутой точке МС1 и процесс численного построения закона углового наведения КА на первом маршруте съемки завершается по превышению заданной длины скана L^ МС1 на земном эл липсоиде. Момент времени ti® начала второго маршрута съемки (МС2) определяется из условия достижения дальности D наблюдения точки A при значении угла 52 = -5/2 между траверсом этой точки на спутник и ортом целеуказания v s на точку A. Для совпадения МС1 и МС2 на земном эллипсоиде шаги численного построения закона углового наведения КА на втором маршруте выполняются также с периодом Ts , но с обеспечением постоянства дальности наблюдения D при начальном азимуте A(t^) за счет итерационной вариации значения продольной СДИ Wyi , когда компоненты вектора СДИ в точке Oi (0,0) определяются из условий (9), ортогональности в этой точке вектора СДИ и оси O1z1 СК поля изображения, а также совпадения следа оси визирования телескопа на земном эллипсоиде с центральной линией МС1. Процесс такого построения закона углового наведения на втором маршруте завершается по превышению длины Li? = L(S1) МС2.

Аналитическое представление законов углового наведения спутника в ИСК при известных численных данных для двух маршрутов сканирующей стереосъемки основывается на интерполяции этих данных векторной функцией МПР G как векторного сплайна седьмого порядка с 8 трехмерными столбцами коэффициентов, которые вычисляются на основе (2) и (3) с помощью аналитических соотношений [14]. Краевые условия для поворотного маневра КА между этими маршрутами стереосъемки рассчитываются также на основе явных аналитических соотношений.

Синтез закона углового наведения спутника при выполнении ПМ на интервале времени t Е [ t i p , t p ] с известными краевыми условиями Л ( t? ) = Л _ ; о ( t p ) = о _ ; £ ( t? ) = £ , ;

Л (tp) = Л f; о (tp) = о f; £ (tp) = £ f; е (t р) = е f выполняется при ограничениях на модули векторов его угловой скорости to (t), углового ускорения £ (t) и производной £ (t) по времени. При балансе СУО по вектору КМ Go с условием Go = 0 модель динамики его углового движения принимает вид to = £ с вектором углового ускорения £ = J-1M8, а модель углового движения – кинематическое представление

Л = Л о о /2; О = £; £ = £* = v . (11)

Разработанный закон углового наведения КА при поворотном маневре основывается на необходимом и достаточном условии разрешимости классической задачи Дарбу. Здесь решение представляется как результат сложения трех од- новременно происходящих элементарных поворотов «вложенных» базисов Ek вокруг ортов ek , k = 1 ^ 3 осей Эйлера, положение которых определяется по краевым условиям (10) модели (11). При этом кватернион Л(t) определяется произведением Л (t) = Л i ° Л1( t) ° Л 2( t) ° Л 3( t) , где Лk (t) = (cos(фk (t)/2), ek sin(фk (t)/2)), функция фk (t) определяет угол k -го поворота, k = 1 ^ 3. Векторы ю(t), e(t), g*(t) = g(t) представляются в аналитическом виде при задании сплайнов ф k(t) различных порядков с использованием в общем случае трех участков заданного интервала ПМ [14]: 1) участок разгона с оптимизацией по быстродействию при ограничениях, где КА из заданных краевых условий на левом конце траектории переводится на движение с постоянным вектором угловой скорости по орту е3 ; 2) участок движения с вектором угловой скорости по орту е3; 3) завершающий участок движения КА с гарантированным выполнением заданных краевых условий на правом конце траектории ПМ при использовании векторных сплайнов шестого порядка. При этом все параметры сплайнов ф k(t) вычисляются по явным соотношениям.

ЗАКОНЫ УПРАВЛЕНИЯ СГК

Отсчет углов гиродинов р в схеме 2-SPE представлен на рис. 6. Все внутр ^p енние сингулярные состояния этой схемы СГК являются проходимыми, применяемый явный закон настройки СГК позволяет исключить избыточность данного кластера с вектором КМ H = h g h ( P ) . При проекциях ортов КМ гиродинов X 1 = COS Р 1 ; X ₂ = COS Р ₂ ; У 1 = sin Р 1 ; у 2 = sin Р ₂ ; x ₃ = sin Р ₃ ; x ₄ = sin Р ₄ ; z ₃ = cos Р ₃ ; z ₄ = cos Р ₄ (см. рис. 6) и введении обозначений

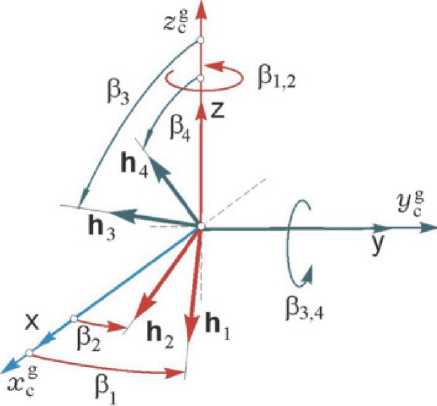
Рис. 6. Отсчет углов ГД схемы 2-SPE

~ x 12 = x 1 ⁺ x 2 ; y 12 = y 1 ⁺ y 2 ; x 12

x 12 ^/ V⁴   y 12 ;

~ x34   x3 + x4 ; z34   z3 + z4 ; x34

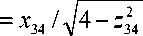
функция распределения вектора нормированного КМ СГК h ( P ) между парами ГД с фиксированным параметром р принимается в виде

fр (Р) = ^12 — ^34 + Rev34 — 1) = 0 , где 0 < р < 1. При этом внутри области S остаются сингулярными два одномерных множества

Sу = {(х /(2р))2 + (z/2)2 = 1, х < 0; у = 0,

• I У 1 1 = I у 2 1 = ^1};

Sz = {(х/(2р))2 + (у/2)2 = 1, х > 0; z = 0,

I ^ al=|2 4 | = 1}, где х = x12 + x34, у = y12, z = z34 и учтены направления запрещенного перераспределения вектора КМ СГК между парами ГД при условии h(P( t))e S yz = S у и S z. Явный закон настройки СГК по схеме 2-SPE принимается в фор- ме D+f р (Р) = Фр (f р (P),h(p)). Здесь функция

Ф р ( • ) ^

;- Sat^ , u f р (Р))   h(p) e S \ Q yz;

_ фр Relh(as, lр, rs) h(e) g Q s, s = у, z,

D+ - символ правой производной по времени, фр, цр и /р - положительные параметры и используются нелинейные функции

Relh( a , l _р , x )

- 1

^x > ^{- 1} р , ^x <  ^l р ;

Relh(as,lр,rs(p(to) = as g {-1;1} ;

ry = Mn(p, -p2 -n), rz = Mn(p3 -p4 -n) ;

a

p

M n ( a ) -

I a | < n;

a - 2n Sign(a) | a | > n.

Для однозначного определения столбца u g = {u gp } к основному соотношению M ^g =- h g A _h ( P ) u ^g добавляется закон настройки СГК в форме

(ар, ■•) = Фр (/р (P), h(P)), (12)

где столбец ар(Р) = df 3 (Р)/ др . При заданном векторе Mg получается система линейных уравнений {Ah (P),(ар)t}u8 = {-Mg / hg, Фр (•)} относительно компонентов ugp столбца ug = {up}, которая разрешается по явным аналитическим соотношениям. При цифровом управлении ug (t) = {ug;t (t)} с периодом Tu и столбце дискретных команд ug формируют ся кусочно-постоянные функции ug^ (t) = upt

∀ t ∈ [ t_k , t_{k + 1}) , t_{k + 1} = t_k + T_u , k ∈ N₀ , управления гиродинами и СГК создает вектор управляющего гироскопического момента (6) с законом настойки (12) в дискретной форме.

ЗАКОНЫ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ СПУТНИКА

При законе наведения КА Л p ( t ), Ю p ( t ), £ p ( t ) в ИСК кватерниону Е = ( e ₀, е ) = Л p ° Л с вектором e = { e_i } соответствует вектор параметров Эйлера E = { e ₀, e } и матрица угловой погрешности C ^e( E ) = I ₃ - 2[ e × ] Q _e ^t , где Q _e = I ₃ e ₀ + [ e × ] . После дискретной фильтрации измеренных с периодом T_q значений векторов углового рассогласования ε _l = - 2 e _{0 l} e _l и угловой скорости ω _l , l ∈ N₀ , формируются значения векторов ε ^f k и ω ^f _k , k ∈ N₀ , которые применяются в цифровом законе управления СГК с периодом T_u : g к + 1 = ^Bg k ⁺ С е k ;    m k = Kg k + P e k ;

,                                 ,(13)

Mf =®f x G: + J(С:ep + [С:ropx]to^ + mJ, k        k       k           k ^         k ^       kk где Go = Jωf +H и матрица Ce = Ce(E ) .

k   kk        kk

КОМПЬЮТЕРНАЯ ИМИТАЦИЯ

Компьютерная имитация была выполнена для спутника землеобзора на солнечно-синхронной орбите (ССО) высотой 720 км. Тензор инерции КА J = diag{812; 587; 910} кгм², в его модели (1), (5) значения парциальных частот первого тона Ω ¹ _j и декремента δ упругих колебаний каждой панели СБ таковы: Ω ¹ _j ≈ 0.6 р/c (частота ≈ 0.1 Гц) и δ = 0.01 . Учитывался шум БИНС с СКО c ^a = 1 угл. сек и о^ю = 0.33 - 10 ^{- 4} град/с при измерении соответственно углового положения и угловой скорости КА с периодом T q = 1/8 с, дискретная фильтрация измерений выполнялась с этим же периодом, а цифровое управление СГК при модуле КМ ГД h_g = 100 Нмс формировалось с периодом T _u = 1 / 4 с. Учитывались ограничения | ω ( t ) | ≤ 1.5 град/с и | ε ( t ) | ≤ 0.2 град/с² на модули векторов угловой скорости и углового ускорения корпуса КА, обусловленные ограниченными ресурсами СГК по допустимой области вариации вектора его КМ и допустимым скоростям угловых перемещений ГД.

Маршруты съемки, в том числе стереосъемки с углом конвергенции δ = 30 град, представлены на рис. 7. Здесь при отчете времени от момента прохождения КА восходящего узла орбиты отмечены

• _•    трассовая сканирующая съемка, маршрут Триполи , t ∈ [539.25, 549.25] с;

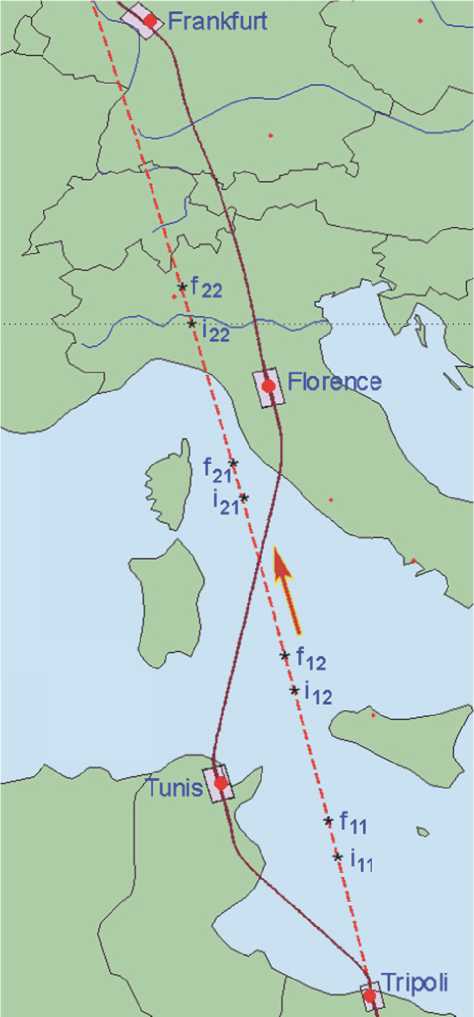
Рис. 7. Маршруты съемки на карте

• •    ПМ маршрут Триполи ⇒ стерео МС1 Тунис , t ∈ [549.25, 580.75] с;

• •    стерео МС1 Тунис с азимутом A = - 13.42 град, точки i ₁₁и f ₁₁, t ∈ [580.75, 591.25] с;

• •    ПМ стерео МС1 Тунис ⇒ стерео МС2 Тунис , t ∈ [591.25,647.25] с;

• •    стерео МС2 Тунис с азимутом A = - 13.42 град, точки i ₁₂и f ₁₂, t ∈ [647.25, 658] с;

• •    ПМ стерео МС2 Тунис ⇒ стерео МС1 Флоренция , t ∈ [658, 690.75] с;

• •    стерео МС1 Флоренция с азимутом A = - 14.18 град, точки i ₂₁ и f ₂₁, t ∈ [690.75,701.5] с;

• •    ПМ стерео МС1 Флоренция ⇒ стерео МС2 Флоренция, t ∈ [701.5, 756] с;

• •    стерео МС2 Флоренция с азимутом

  

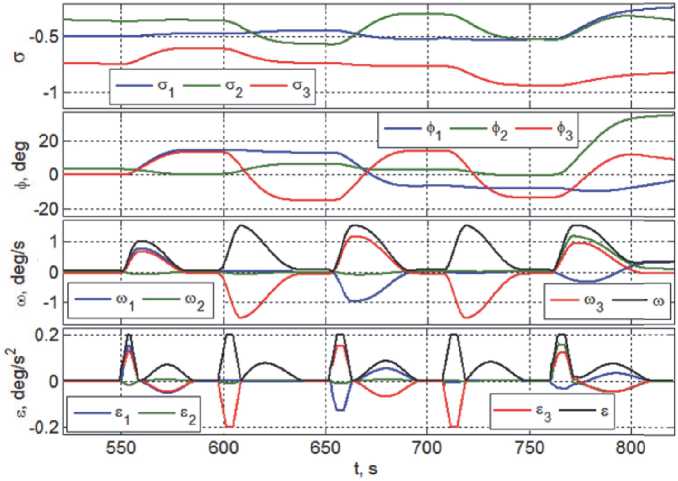
  Рис. 8. Закон углового наведения КА для выполнения заданных маршрутов съемки

  
  
  

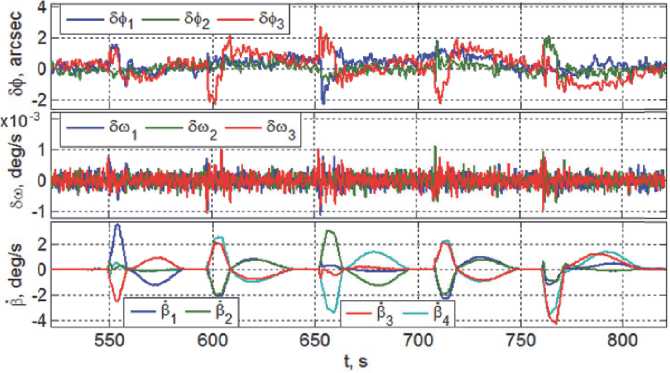
  Рис. 9. Погрешности реализации закона наведения и угловые скорости гиродинов

  
  

A = - 14.18 град, точки i ₂₂ и f ₂₂, t ∈ [756, 766.75] с;

• •    ПМ стерео МС2 Флоренция ⇒ маршрут Франкфурт , t ∈ [766.75, 810.75] с;

• _•    съемка с выравниванием, маршрут Франкфурт с азимутом A = –45 град, t ∈ [810.75,820.75] с.

На рис. 8 приведен синтезированный закон наведения спутника для выполнения маршрутов сканирующей съемки указанных видов и поворотных маневров между ними. Здесь первые два графика представляют ориентацию ССК относительно ИСК (вектор МПР σ = { σ _i } ) и ОСК (углы крена φ ₁ = γ , синий цвет; рыскания φ ₂ = ψ , зеленый цвет и тангажа φ ₃ = θ , красный цвет). На следующих двух графиках представлены изменения компонентов векторов угловой скорости и углового ускорения, помеченные такими же цветами, и дополнительно приведены вариации модулей этих векторов, отмеченные черным цветом.

Графические результаты на рис. 9 характеризуют эффективность работы гиро-силовой СУО с синтезированными алгоритмами цифрового управления СГК при реализации рассчитанного закона наведения, см. рис. 8. Здесь приведены компоненты векторов погрешностей Зф = { Зф i } = 2 e _о е и 3 ® = { 3® i } = to — С ^е ( E ) to p (t ) по углам и угловым скоростям, помеченные указанными выше цветами, а также угловые скорости гиродинов. Выполненный анализ движения изображения в ФП телескопа [15] для всех рассмотренных маршрутов сканирующей съемки показал, что реализованная СУО точность наведения и стабилизации углового движения спутника зем-леобзора гарантирует отсутствие «смаза» получаемого электронного изображения для всего набора матриц оптико-электронных преобразователей.

ЗАКЛЮЧЕНИЕ

Разработаны методы синтеза законов наведения и цифрового гиросилового управления ориентацией спутника землеобзора при сканирующей стереоскопической съемке. Законы углового наведения основаны на аналитических соотношениях, связывающих движение изображения в ФП телескопа с кинематическими параметрами пространственного перемещения спутника относительно земной поверхности при обеспечении постоянных значений дальности наблюдения и угла конвергенции в процессе сканировании с двух ракурсов. Разработанные методы цифрового управления ориентацией КА с помощью минимально-избыточного кластера гиродинов обеспечивают формирование такого управления по явным аналитическим соотношениям. Представлены результаты компьютерной имитации стереосъемки двух участков земной поверхности, выполняемых спутником землеобзора на ССО. Показано, что точность гиросиловой СУО спутника позволяет получать электронные изображения высокого качества при стереоскопической съемке.