Наведение и управление космическим роботом при перелетах в низкоорбитальной группировке мини-спутников землеобзора

Современные тенденции развития космических систем дистанционного зондирования Земли состоят в переходе от полноразмерных космических аппаратов (КА) к группировкам оптико-электронных (SkySat) и радиолокационных (Capella-36) мини-спутников с потребной периодичностью землеобзора с низких орбит [1] – [4].

При сроке службы до 5 лет такие спутники имеют массу до 500 кг и крупногабаритные панели солнечных батарей для энергоснабжения бортовой аппаратуры, включая систему управления движением (СУД) с электрореактивными двигательными установками (ЭДУ) и силовым гироскопическим кластером (СГК) на основе ги-родинов (ГД). Измерение координат движения КА выполняется бесплатформенной инерциальной навигационной системой (БИНС) с коррекцией сигналами от навигационных спутников

ГЛОНАСС/GPS и кластера астрономических датчиков (КАД).

Полётная дозаправка ЭДУ топливом экономически невыгодна для «дешевых» микро-спутников массой до 100 кг, но для мини-спутников, оснащенных «дорогой» бортовой аппаратурой (телескоп, БИНС, КАД, СГК, ЭДУ и др.), необходимо изучить аспекты продления срока их службы до 20 лет за счет дозаправки ЭДУ топливом с помощью космических роботов-манипуляторов (КРМ). Для орбитальной группировки миниспутников землеобзора на низких солнечно-синхронных орбитах (CCO), по три КА в окрестности каждой базовой орбитальной плоскости [4], актуальны задачи управления КРМ при его сближении с мини-спутниками. В статье исследуется задача выполнения таких маневров КРМ в окрестности одной базовой орбитальной плоскости.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Применяются стандартные системы координат (СК): инерциальная (ИСК O _ffi X i Y i Z¹ , базис I _@ с ортами i i , i = 1,2,3 = 1 ^ 3 ), орбитальная (ОСК О x ° у ° z ° , базис О с ортами радиали r ° , трансверсали т ° и бинормали n ° ) и связанная с КРМ (ССК О xyz , базис B ) системы координат с началом в его центре масс Ο . Предполагается, что вектор тяги Р ^е плазменной ЭДУ направлен вдоль оси Ο y ССК. Ориентация ССК в ИСК определяется кватернионом Л и вектором о = { о i } модифицированных параметров Родрига (МПР), а ориентация ССК в ОСК - углами рыскания ф 1 , крена ф ₂ и тангажа ф ₃ в последовательности 132. Используются векторы угловой скорости го и ускорения £ , а также обозначения { • } = col( - ) ,

[ • ] = line ( • ) и ( • ) * , [ -x ] для векторов и матриц.

Корпус КРМ считается твёрдым телом с массой m и тензором инерции J , при векторах по- ложения r и скорости v модель его движения в

ИСК имеет вид

r‘ + tox г = v; m (v‘ + to x v) = Pе + Fd;

Л = Л oto/2; Jto + toxG = Mg + Md.

Здесь вектор G = J ω + H , где H – вектор кинетического момента (КМ) СГК и M ^g = — H ‘ представляет вектор его управляющего момента, F ^d и M ^d - векторы внешних возмущающих сил и моментов, а ( • ) ‘ - символ локальной производной по времени.

При законе углового наведения Л ^р( t ), to ^р( t ), е ^р( t ) погрешность ориентации КРМ определяется кватернионом E = ( e ₀, е ) = Л ^Р о Л , где вектор е = { e i } , матрицей ошибки ориентации С ^е = 1 ₃ — 2[ e x ] Q ‘ , где Q _е = 1 ₃ е ₀ + [e x ] , вектором МПР О ^е = е ^е 1ап(Ф ^е /4) с ортом Эйлера е ^е и углом Ф ^е собственного поворота, а также вектором угловой погрешности 5 ф ={5 ф _/ }={4о ® } . Вектор ошибки по угловой скорости КРМ определяется соотношением 5 to = to — C ^е to ^р ( t ) .

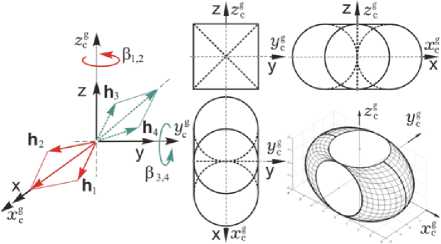
Рис. 1. Схема СГК и область вариации его КМ

В системе управления движением робота применяется СГК с четырьмя ГД, рис. 1. Вектор КМ p -го ГД h p ( в p ) = h g h p ( в p ) имеет орт h _p и кинетический момент h_g, одинаковый для всех гиродинов. При таких обозначениях вектор h ( P ) нормированного КМ кластера ГД представляется в виде h ( P ) = Е h p ( в p ) , где столбец в = { в }, p = 1 ^ 4 , а вектор управляющего момента СГК формируется по соотношениям M ^g =— H ‘ = — h_g A _h( P ) u ^g, P = u ^g с матрицей Якоби A _h ( в ) = d h ( P )/ d p .

При дискретной фильтрации вектора углового рассогласования e ^a =— 5 ф значения вектора £ k ^f при t = t_k с периодом T u , k e N₀ = [0,1,2,..) применяются в цифровом законе управления СГК g k + i = В g k + C e k ^f ; m _k = К ( g _k + P e a ^f );       (2)

Mk =to k x Gk + J(Ck ek + [(Cktop )x]to k + mk).

Далее вектор M ^g аналитически преобразуется в вектор u^g_k цифрового управления скоростями ГД.

В столбце оскулирующих координат q _r = {^ .t. to _n ,p,e,u } вектора r расположения КА на орбите выделяются (i) три элемента её ориентации - долгота восходящего узла (ВУ) Q, наклонение i и аргумент перигея ω_π орбиты и (ii) три элемента, определяющих размеры, форму орбиты и положение КА на орбите – фокальный параметр p , эксцентриситет e и аргумент широты орбиты u ( t ) - иногда называемой «орбитальной широтой», отсчитываемой от линии узлов в экваториальной плоскости и связанной с истинной аномалия v ( t ) соотношением и ( t ) = to n + v ( t ).

При сближении КРМ с тремя мини-спутниками (целями) в окрестности базовой плоскости для пополнения топливом их ЭДУ манёвры КРМ состоят в двух перелётах между орбитами этих КА в группировке. Каждый перелёт содержит 3 этапа: (i) поворот плоскости орбиты КРМ до совмещения её с плоскостью орбиты очередной цели, (ii) фазировка положения КРМ с такой целью на компланарных орбитах и (iii) завершающее сближение КРМ с целью.

Задача состоит в разработке законов наведения и управления КРМ с оценкой времени и затрат рабочего тела ЭДУ на каждом этапе перелета между мини-спутниками. Для её решения используются известные методы механики управляемого космического полета [5] –[9], включая модель движения и встречи двух КА в гравитационном поле (уравнения Клохес-си-Уилтшира [10]) и дальнейшее развитие этой модели с учётом второй гармоники гравитационного потенциала Земли – уравнения Швай-гарта-Седвика [11].

НАВЕДЕНИЕ И УПРАВЛЕНИЕ ПРИ ИЗМЕНЕНИИ ПЛОСКОСТИ ОРБИТЫ

В теории мгновенных импульсов скорости поступательного движения КА решение задачи поворота плоскости орбиты [9] основано на изменении направления трансверсальной компоненты вектора скорости v 1 КРМ в плоскости первой орбиты (рис. 2. a , синий цвет) на угол AQ для получения вектора скорости v ₂ в плоскости второй орбиты, см. рис. 2 a , зелёный цвет.

Когда КРМ находится на линии пересечения этих орбит в одной из двух точек апекса – наиболее удалённых от земного экватора точках a _n в северном либо a _s в южном полушариях небесной сферы (см. рис. 2 a ), модуль требуемого импульса скорости Av = |А v | = | v ₂ — v ₁ | вычисляется по соотношению Av = 2v ₁ sin( AQ /2) , где v 1 = | v 1 | . При малой тяге ЭДУ требуемый

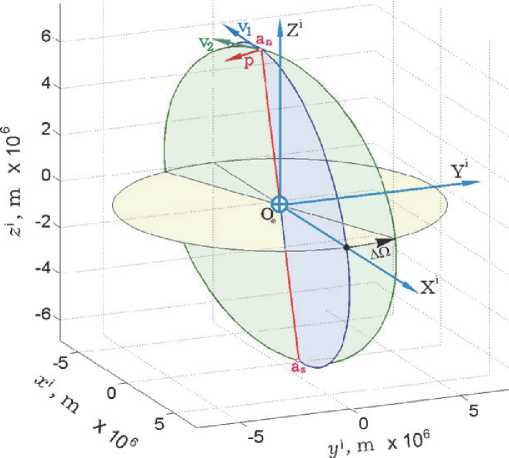
Рис. 2 a . Схема изменения долготы ВУ орбиты

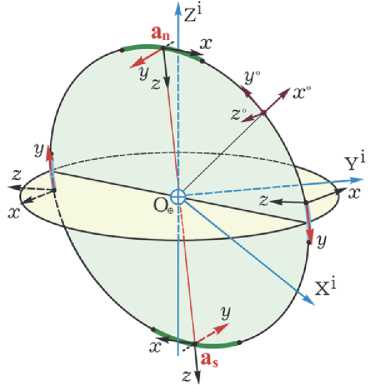
Рис. 2 b. Схема управления пространственным движением КРМ при орбитальном перелете импульс скорости не может быть реализован на малом интервале времени, при котором ориентацию КА можно считать постоянной. Поэтому возникает важная задача определения переменного направления вектора тяги ЭДУ, при котором реализуется требуемый маневр перехода КРМ в заданную плоскость орбиты. Вектор импульса скорости A v принадлежит плоскости, касательной к обеим орбитам и, следовательно, перпендикулярен линии пересечения плоскостей этих орбит. При AQ ^ 0 это условие сохраняется, а положение линии пересечения плоскостей стремится к вектору r положения КРМ с ортом r° = {r1°, r2°, r3°} в точке соответствующего апекса.

Изменение долготы ВУ орбиты КРМ представляется в ИСК её поворотом вокруг оси вращения Земли c ортом i ₃ = {0,0,1}. Все точки апексов орбит КРМ располагаются на окружностях в плоскостях, параллельных плоскости экватора, а орт p управляющего ускорения вдоль оси О у ССК робота всегда направлен от оси O _$ Z i ИСК (рис. 2 b ) и принадлежит плоскости Q ( r ^o, i 3 ) . Следовательно, орт p вектора тяги ЭДУ робота в ИСК должен формироваться по соотношению p = b /b , где вектор b = ( i ₃ х r o ) х r ^o и b = | b | . В результате получается закон углового наведения вектора тяги плазменной ЭДУ P ^e = P m p sign r ₃ o , где параметр P m представляет номинальное значение тяги.

При таком законе наведения тяги ЭДУ эффективность перемещения долготы ВУ уменьшается при отдалении КРМ от соответствующей точки апекса. Поэтому применять этот закон рационально только вблизи апексов, времен- ные интервалы прохождения которых определяются прогнозом орбитального перемещения КРМ. Прогноз выполняется на каждом витке орбиты робота на основе аналитических соотношений при использовании измерений его положения и скорости. Здесь определяются моменты времени tn и ts прохождения северного (индекс n ) и южного (индекс s ) апексов, а также интервалы времени включения ЭДУ Vt E [tj — Td,tj + Td ], j = n,s с половинным значением Td в полной длительности Sd = 2Td включения ЭДУ. Такие интервалы отображаются участками орбиты КРМ, выделенными зелёным цветом на рис. 2 b.

Угловое наведение КРМ в ИСК определяется ортогональной матрицей ориентации A ^b = { a t } при столбцах a 1 = r ° х p , a ₂ = p и a ₃ = a 1 х p , кватернионом Л и вектором о МПР. На каждом витке орбиты в окрестности её восходящего и нисходящего узлов выполняется два разворота КРМ на угол ® 180 град (см. рис. 2 b, где такие участки орбиты выделены голубым цветом) с аналитическим назначением краевых условий для корректного перехода КРМ через точки апексов при работающей ЭДУ.

НАВЕДЕНИЕ И УПРАВЛЕНИЕ КРМПРИ ФАЗИРОВКЕ И СБЛИЖЕНИИ

Фазировка выполняется при сближении двух КА, движущихся на близких компланарных орбитах, за счет изменения средней угловой орбитальной скорости одного из них, в данном случае скорости космического робота. В теории мгновенных импульсов скорости фазировка до-

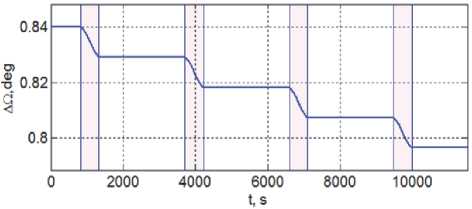
Рис. 3. Изменение разности долготы ВУ орбиты КРМ на первых двух витках сближения

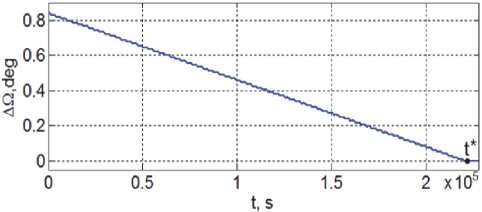
Рис. 4. Изменение разности долготы ВУ орбит КА#1 и космического робота-манипулятора

стигается за счет формирования импульса вектора скорости А v в перигее орбиты КРМ для изменения его средней орбитальной скорости и, через один виток фазирующей орбиты, формирования обратного импульса — А v для возврата КРМ на исходную орбиту [9], причём такие импульсы формируются в соответствующих направлениях орта трансверсали т ° орбиты. Малая тяга ЭДУ учитывается в расчетах параметров фазирующей траектории c центрированием моментов времени включения / выключения ЭДУ относительно момента времени t _π прохождения перигея π орбиты КРМ.

Решение задачи сближения КРМ с точкой «прицеливания» на заданном расстоянии от обслуживаемого мини-спутника начинается с синтеза закона наведения КРМ в поступательном движении. Здесь основными являются параметры разгонного и тормозного мгновенных импульсов скорости КРМ, а также длительность такого манёвра робота при наличии ограничений. Далее применяются известные переходные матрицы уравнений Клохесси-Уилтшира и их модификации с учётом особенностей распределения требуемых импульсов скорости, формируемой плазменной ЭДУ малой тяги, и бортового прогноза влияния возмущений по доступным измерениям [12].

КОМПЬЮТЕРНАЯ ИМИТАЦИЯ

Компьютерная имитация выполнена для перелётов КРМ между смежными орбитами мини-спутников в группировке трёх КА на солнечно-синхронных орбитах, разнесенных по долготе ВУ на угол AQ = 0,84 град. Параметры этой группировки соответствуют площадной съёмке акватории Мраморного моря и окрестностей Стамбула, детали представлены в [4]. Здесь использованы модели (1) и (2) движения КРМ c массой 1500 кг и тензором инерции J = diag(1600,1200,1800) кгм² с учётом гравитационных возмущений от Луны, Солнца и второй гармоники геопотенциала, ЭДУ с тягой

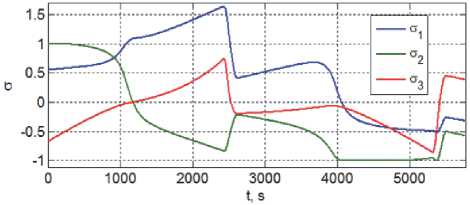
Рис. 5. Вектор МПР при программных разворотах робота на первом витке орбиты

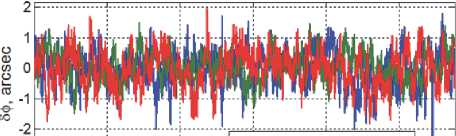
8ф1 ----8ф2----8ф3

0       1000     2000     3000     4000     5000

1,5

Рис. 7. Вектор угловой ошибки при разворотах космического робота на первом витке

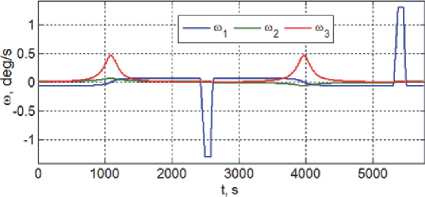
Рис. 6. Вектор наведения по угловой скорости при разворотах космического робота на первом витке

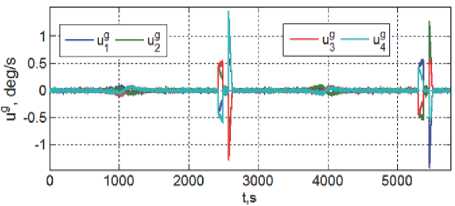
Рис. 8. Вектор управления гиродинами в составе СГК на первом витке орбиты

Pm = 6 Н при скорости истечения рабочего тела 17363,7 м/с. Имитация поворотных манёвров КРМ выполнена при использовании СГК с собственным кинетическим моментом каждого гиродина hg = 30 Нмс и цифровом управлении с периодом 1„ = 0,25 с.

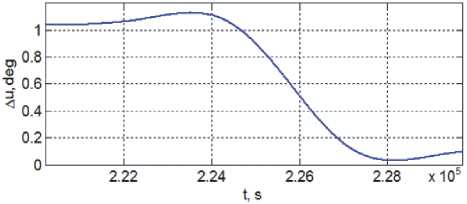
Рис. 9. Разность орбитальной широты КА#1 и КРМ

Рисунок 3 представляет изменения разности долготы ВУ орбиты КРМ AQ на первых двух витках орбиты при включениях ЭДУ в окрестности каждого апекса, которые выделены розовым цветом. Изменение разности долготы ВУ орбиты КРМ AQ( t ) демонстрируется на рис. 4, где перелёт между орбитами КА#1 и КА#2 завершается в момент времени t * = 220200 с (длительность T m = 2, 5 сут) при расходе рабочего тела 13,26 кг. На рисунках 5 и 6 представлены

Возмущения, ошибки прогноза и погрешности ориентации КРМ при отработке заданного импульса скорости с его «распределением» на интервал времени, пропорциональном тяге ЭДУ, не позволяют выполнить фазировку с высокой точностью, необходимы дополнительные этапы сближения с целью, детально представленные на рис. 10 – 13, где модули отмечены черным цветом.

На рисунке 14 приведена общая картина изменения модулей векторов дальности и разности скоростей КРМ и цели на указанных завершающих этапах маневрирования КРМ. Здесь три синие пунктирные вертикальные линии разделяют: (i) поворот плоскости орбиты и фа-зировку (левая линия), (ii) фазировку и первый этап сближения (средняя линия) и, наконец, (iii) самая правая линия разделяет последовательно выполняемые первый и второй дополнительные этапы сближения.

ЗАКЛЮЧЕНИЕ

Кратко описаны разработанные алгоритмы наведения и управления движением космического робота при его сближении с мини-спутниками на низких солнечно-синхронных орбитах в группировке землеобзора и представлены результаты

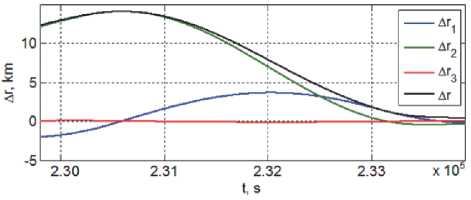
Рис. 10. Вектор дальности КРМ от цели

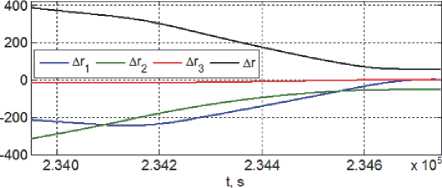
Рис. 12. Вектор дальности КРМ от цели на втором этапе сближения

на первом этапе сближения

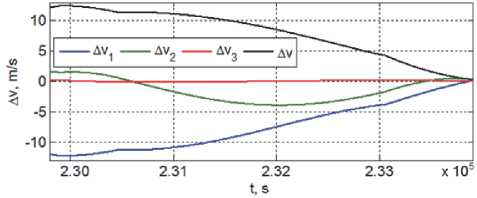
Рис. 11. Вектор разности скоростей КРМ и цели на первом этапе сближения

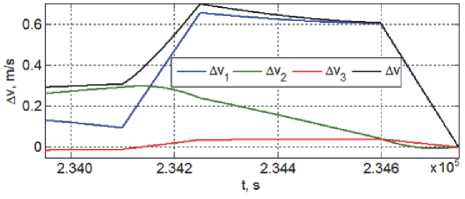
Рис. 13. Вектор разности скоростей КРМ

программные изменения векторов МПР а и угловой скорости to при двух разворотах КРМ на первом витке орбиты. Векторы угловой погрешности стабилизации этого движения КРМ и цифровых командных скоростей ГД при таких разворотах приведены на рис. 7 и 8. Результаты имитации фазировки КРМ при его сближении с КА#1 в плоскости орбиты представлены изменением разности орбитальной широты на рис. 9.

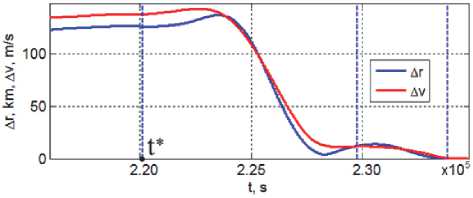
Рис. 14. Дальность и разность скоростей

компьютерной имитации. Получены оценки продолжительности перелётов робота и расхода топлива электрореактивной двигательной установки.

Наиболее важными новыми результатами являются цифровые алгоритмы наведения и управления космическим роботом при изменении долготы восходящего узла его орбитальной плоскости.