Necessary conditions for the propagation of two modes, Lp01 and Lp11, in a step-index optical fiber with a Kerr nonlinearity

In one of the first works [1] devoted to analyzing the effect on the mode parameters of changes in the refractive index profile of a step-index optical fiber due to Kerr nonlinearity, a model of the refractive index profile of such a fiber was presented, a numerical solution was found for the fundamental mode and calculation data were given for the dependencies of the parameters of this mode on the normalized frequency of the stepped optical fiber and optical power. At the same time, a dependency analysis was performed for relatively small values of optical power of up to 0.4 MW. However, the intensive development of a technique for forming ultrashort high-power optical pulses with fiber lasers [2–4] and a wide range of technologies for their use [5–7] means that it is important to take nonlinearity into account when determining the parameters of the modes propagating in optical fibers. From the point of view of analyzing processes and modelling the propagation of pulses in an optical fiber, analytical solutions are of particular interest in this regard.

An analytical solution for the fundamental mode was obtained [8,9] for the above problem by considering it on the basis of the Gauss approximation method [10–13], and the dispersion characteristics of an optical fiber were considered for relatively large optical powers. The Gauss approximation method is based on an approximation of the distribution of the mode field using Laguerre–Gauss functions and a search for the parameter of this approximation (the equivalent radius of the mode spot) providing the best approximation. When using this method, it is assumed that the distribution of the mode field is known. This allows us to take into account changes in the profile of the refractive index due to the action of non-linear factors, which in turn allows this method to be used to obtain analytical expressions for optical fiber mode parameters with a given refractive index profile, taking nonlinearity into account.

In previous papers [8, 9, 14], the Gauss approximation method was used to obtain analytical solutions for the LP01 and LP11 modes of a stepped optical fiber with Kerr nonlinearity, given that only one of these modes was distributed in it. The work investigated the necessary conditions for the excitation of a higher-order mode in a singlemode stepped optical fiber with Kerr nonlinearity, using the Gauss approximation method. At the same time, for a multimode optical fiber, a more characteristic feature is the excitation and propagation of several modes simultaneously. In the present article, the necessary conditions are considered for the propagation of two linearly polarized modes, LP01 and LP11, in a stepped optical fiber with Kerr nonlinearity, assuming that only these two directed modes propagate in the fiber. First, using an approximate analytical solution, we find estimates for the parameters of the modes, the conditions for the joint propagation of these modes in the optical fiber, and the distributions of the mode fields. These estimates are calculated by solving a system of nonlinear equations obtained for the linearly polarized modes LP01 and LP11 of a step-index optical fiber with Kerr nonlinearity, provided that only these two modes propagate. Then, using the obtained approximations for the distributions of the mode fields, the profile of the refractive index changed by the Kerr nonlinearity is determined, for which the required necessary conditions are specified using the method of mixed finite elements. This approach is shown to be effective in refining the es- timates of the parameters of guided modes of light guides. A well-known variant of the mixed finite element method and the algorithm for its implementation, described in detail in the papers [15], is applied here.

1. Fundamentals of the Gauss approximation method

The Gauss approximation is based on a representation of the field of a fiber light guide by linearly polarized modes, the radial distribution of which is described by Laguerre-Gauss functions [12]

2. The model of a refractive index profile of optical fiber with a Kerr nonlinearity

The refraction index profile of a step-index optical fiber, without taking into account the nonlinearity factor, is described as follows [12].

n s ( r ) =

n _c , n c , l ,

r < a r > a

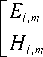
| sin l ф|

= Fi,m ( x ) 5    , f exp[ - j ( ю t -P I , mz )],

I cos l ф

F l , m ( x ) = x ^l 2 L m - 1 ( x ) exp( - x /2), X = R 2/ R l 2 m ,

where F l , m ( r ) – is the radial distribution function of the mode field of radial ordermand azimuthal order l ; p _l , _m - is the propagation constant of the mode, of radial order m and azimuthal order l ; a – is the radius of the core of the optical fiber; r l , m – is the equivalent radius of the spot of the mode; R l , m = r l , m / a – is the normalized equivalent radius of the mode spot; R = r / a – is the normalized value of the radial coordinate; L ⁽ _m ^{l )}( y ) – is the Laguerre polynomial of order m and l , and argument y ; r – is the radial coordinate; ф - is the azimuthal coordinate; and z - is the longitudinal coordinate directed along the fiber axis.

This representation is valid for weakly guided optical fibers for which the propagation constant of a linearly polarized mode of radial order m and azimuthal order l can be determined from the expression [12, 13].

j j k2n2 (x)■ Fi2m (x)■ cos2 (lФ)dxdф в2 m = —---2------------------------+ l,m              го 2n j j F 2m (x)■ cos2 (lф)dxdф              (2)

+ 2 Cl,m a2 ■ Rl2 m ’

where n ( r ) – is the profile of the refractive index of the optical fiber; and k – is the propagation constant in free space.

The constant C l , m , which depends only on the order of the mode, is calculated by the formula [13].

(m + 1 - 1)!

C,_m = m ⁽)- + ( m + 1 - 1) ^l ’ m       2( m - 1)!

+ ₁ 2 g ( i + 1 - 1)!

i = 0 i ^!

(m +1 - 2)!

2( m - 2)! ⁺

.

For a given profile of the refractive index, an analytical expression can be obtained for the mode propagation constant from (2), after integration. Using the condition dp _lm / d R , _m = 0 after differentiation, a characteristic equation is then found with respect to the equivalent spot radius of the mode [12].

The refractive index profile taking into account the Kerr nonlinearity is described by the formula [16].

n ( r ) = n s ( r ) + n 2 1 ( r ),

where n 2 is the Kerr nonlinearity parameter, and I ( r ) is the intensity distribution of optical radiation along the fiber’s radius.

In the case of propagation in the light guide of the two modes LP 01 and LP 11 , we can assume that

I ( r ) =

P m

4 n a ²

F 0,1 ( x ) q 0,1

R 0 1

F ,1 ( x L,     1 ²

—"—Cos Ф , (4) Rm

where P m is the power of the optical radiation introduced into the light guide; and q 0,1 , q 1,1 are coefficients that take into account the distribution of the input power of optical radiation between the corresponding modes.

The equivalent radius of the mode spot is two times smaller than the radius of the spot of the corresponding mode [17]. Given this, we introduce the notation

I m

n 2 P m

4 n a ²

After substituting (3), (5) into (4), we obtain the following formula for the profile of the refractive index

, x , т Гq0,1 ■ Fo21(x), ~ I----------F0,1(x) n (r) = ns(r) + Im -----2-----+ 2Vq0,1 ■ q1,1 —

_     R 0,1

F1,1 (x)            q1,1 ■ F1,1 (x)

^X —--Cos ф +------- Cos ф .

R1,1

3. The system of nonlinear characteristic equations for the equivalent spot radii of the LP01 and LP11 modes

In general, the system of nonlinear characteristic equations for determining the equivalent spot radii of the LP 01 and LP 11 modes of a step-index optical fiber with a Kerr nonlinearity, provided that only these two modes propagate in the light guide, can be written as [18]

Y 0 ( x 0,1 , x 1,1 ) = 0, ^ 1 ( x 0,1 , x 1,1 ) = 0,

where ^( x 0,1 , x 1,1 ) and T 1 ( x 0,1 , x 1,1 ) = 0 are defined according to Table 1 (see Appendix). Here, x ₀ ,1 = 1/ R 02,1 and x 1,1 = 1/ R 121 . Using the formula for the normalized frequency

V2=a2k2NA2, we denote

U ² = V ² INA ².

Expressions in Table 1 of the Appendix completely describe a system of characteristic nonlinear equations for the equivalent spot radii of the LP 01 and LP 11 modes of a step-index optical fiber with a Kerr nonlinearity, provided that only these two modes propagate in the light guide.

To solve the system of nonlinear equations in (7), we use the Newton method [19]. This method has an advantage for this system of equations, since analytical expressions can be obtained for the partial derivatives ∂Ψ 0 / ∂ x 0,1 , ∂Ψ 0 / ∂ x 1,1 and ∂Ψ 1 / ∂ x 0,1 , ∂Ψ 1 / ∂ x 1,1 . These derivatives are defined according to Tables 2 and 3 (see Appendix). The solution of the system of nonlinear equations is found numerically using an iterative process.

• 4.    Necessary conditions for LP 01 and LP 11 mode propagation in step-index optical fiber with Kerr nonlinearity

Here, as an example, we considered a standard optical fiber SMF-28 made of fused silica glass with a step index profile with a core diameter of 8.2 μm and a difference in the refractive indices of the core and cladding of 0.36% [20]. For this optical fiber, according to [21,22], the nonlinear refractive index was taken equal to 2.5∙10^–20 m²/W. The spectral dependences of the refractive indices of the core and cladding were calculated by the Sellmeier formula according to the algorithm given in [23]. For each given power value, by solving the system of nonlinear equations (7), we found estimates of the limits of the range of normalized frequencies for which this solution exists and has physical meaning. The Newton method is used to solve these systems of equations, and estimates are obtained depending on the optical power introduced into the fiber and its distribution between the modes. By using the found parameters x _0,1 = 1/ R ₀²_,1 and x _1,1 = 1/ R ₁²_,1 , the field distributions of the modes under study were calculated according to (1) and (2). Using them and Equation (6), the profile of the refractive index of the fiber was determined, modified by the Kerr nonlinearity. For this profile, the estimates of the boundaries of the range of normalized frequencies were refined using the mixed finite elements method mentioned earlier, in which the necessary conditions for joint propagation of two considered modes in the fiber are fulfilled. Fig. 1 shows an example of the dependences of the parameters x 0,1 , x 1,1 on the normalized frequency of the fiber, for a range of values for the optical power introduced into the fiber and the power evenly distributed between the two studied modes.

It can be seen from Fig. 1 that the lower limit on the normalized frequency range in which there are solutions to the system of equations in (7) is practically independent of the optical power, and is determined by the cutoff condition of the highest order mode. With an error of no more than 5 % as a result of calculations in all cases Vmin = 2.405. With increasing power, the upper limit of this range shifts to lower normalized frequencies. It is natural to assume that the upper limit is due to the selffocusing effect. It is known that for free space, the critical power of self-focusing is approximately determined from the relation:

P f

ε

λ ² 2 π n 0 n 2

where ε is a parameter determined by the shape of the beam. It is shown here that this relationship can also be used for the fundamental mode of a light guide. From (8), we can write for a step-index fiber:

V

max f a⋅NA

≈ const .

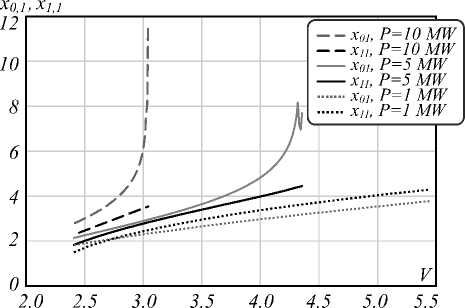
Fig. 1. The dependences of the parameters x 0,1 , x 1,1 on the normalized frequency of the fiber, for a range of values for the optical power introduced into the fiber and the power evenly distributed between the two studied modes

This is confirmed by estimates obtained from solving the system of equations (7) with the subsequent procedure for clarifying them. Fig. 2 shows the curve for the dependencies on the distribution of power between the modes of the normalized estimate of the upper limit of the studied range of normalized frequencies, obtained from the solution of the system of nonlinear equations (7), can be represented as

V p ⁼ V max   q 1 P f 7 a .

Here, it is assumed that q 2 = 1 – q 1 .

Fig. 2 shows that if the fraction of the power of the fundamental mode exceeds approximately 20% of the total power input to the fiber, then the normalized parameter under study is practically independent of the distribution of power between the modes. In this case, it can be assumed that the upper limit of the range is completely determined by the conditions of self-focusing of the fundamental mode of the fiber. Fig. 3 shows the dependence on the power of the fundamental mode of the parameter of the normalized frequency range, in which the necessary conditions are fulfilled, where the parameter

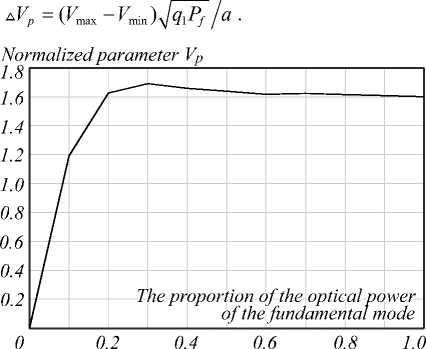
Fig. 2. The curve for the dependencies on the distribution of power between the modes of the normalized estimate of the upper limit of the studied range of normalized frequencies

As shown in Fig. 3, the dependence is almost linear.

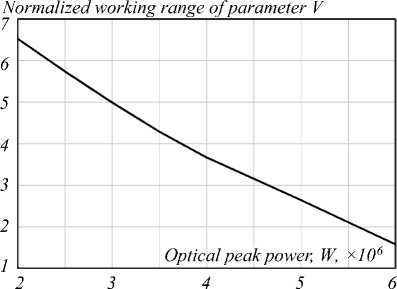
Fig. 3. The dependence of the parameter of the normalized frequency range on the power of the fundamental mode

If we assume that the estimated upper limit on the range of normalized frequencies for which the necessary conditions hold for the joint propagation of the two modes ( LP 01 and LP 11 ) is determined by the conditions of self-focusing of the fundamental mode, then from the definition of the normalized frequency of the step-index optical fiber and Equation from Table 1 (see Appendix), we have the following approximate relationship:

V f «

a ■ NA q1Pmn0n2

q 1 >  0.2.

Fig. 4 shows the dependence of the estimated upper bound of the range of normalized frequencies for which the necessary conditions hold for joint propagation of the two modes LP01 and LP11 in the optical fiber (the threshold values of the normalized frequency). These are calculated from (10), depending on the peak power of the fundamental mode of the optical fiber, and are obtained by solving a system of nonlinear equations (7) and applying the subsequent procedure for their refinement. It can be seen that the curves are almost the same. This allows us to recommend relation (10) to estimate the necessary conditions for propagation for the LP01 and LP11 modes in a step-index optical fiber with a Kerr nonlinearity during the transmission of high-energy optical pulses.

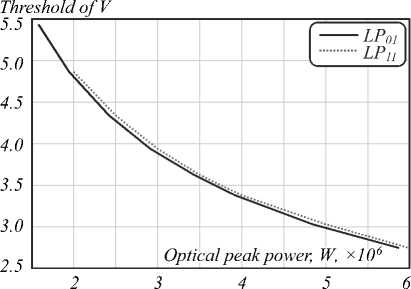
Fig. 4. The dependence of the estimated upper bound of the range of normalized frequencies

Conclusions

This paper presents the results of an analysis of the necessary conditions for propagation in a step-index optical fiber with a Kerr nonlinearity of two modes, LP 01 and LP 11 , during the transmission of high-power optical pulses. All results were obtained by solving a system of two nonlinear equations for these modes, obtained by the Gauss approximation method, and the subsequent use of a procedure for refining these estimates using the method of mixed finite elements. As a result of this analysis, it was shown that the lower limit of the range of normalized frequencies for which there are joint solutions for the two modes under study is determined by the cutoff of a higher order mode, and that its value is 2.405. It is shown that if the fraction of the power of the fundamental mode exceeds 20% of the total optical power introduced into the fiber, the upper limit of the normalized frequency range for which there are joint solutions for these two modes is determined by the condition of self-focusing of the fundamental mode. In this case, the range of normalized frequencies for which the necessary conditions are fulfilled decreases almost directly proportionally to the power of the fundamental mode. An approximate relationship is proposed for estimating the upper limit of the range of normalized frequencies for which the necessary conditions are met for the propagation of two LP 01 and LP 11 modes in a stepped optical fiber with Kerr nonlinearity when transmitting high-power optical pulses.