Нечеткая модель прогноза времени локализации аварийных ситуаций при железнодорожных перевозках

В основу предлагаемой нечеткой модели положены известные понятия теории нечетких множеств, как: любой элемент может принадлежать более, чем одному множеству, а функции принадлежности для разных множеств могут перекрываться. Основное преимущество нечеткой логики для решения нашей задачи состоит в способности схватить нелинейные отношения между входными и выходными переменными без чрезмерных упрощений. База данных, содержит усредненные данные, за пятиминутные периоды по масштабу и продолжительности с момента возникновения по четырем авариям с отопительной системой вагона, и одновременно временную информацию по выходу из аварий. Эта информация получена с использованием сигнально-контрольной аппаратуры и экспертов.

Для того, чтобы отразить нелинейную связь между масштабами опасных ситуаций и временем их локализации, рассеянные точки группируются в семь частично перекрывающихся областей как показано на рис. 1.

Каждая область представляет собой каждое нечеткое правило. Нечеткими правилами являются:

Правило 1. Если масштаб аварии есть очень малый (ОМ), тогда время ее локализации есть очень малое (ОМ).

Правило 2. Если масштаб есть малый (М), тогда время локализации есть малое (М).

Правило 3. Если масштаб есть ниже среднего (НС), тогда время локализации есть ниже среднего (НС).

Правило 4. Если масштаб есть средний (С), тогда время локализации есть среднее (С).

Правило 5. Если масштаб есть выше среднего (ВС), тогда время локализации есть выше среднего (ВС).

Правило 6. Если масштаб есть большой (Б), тогда время локализации есть большое (Б).

Правило 7. Если масштаб есть очень большой (ОБ), тогда время локализации есть очень большое (ОБ).

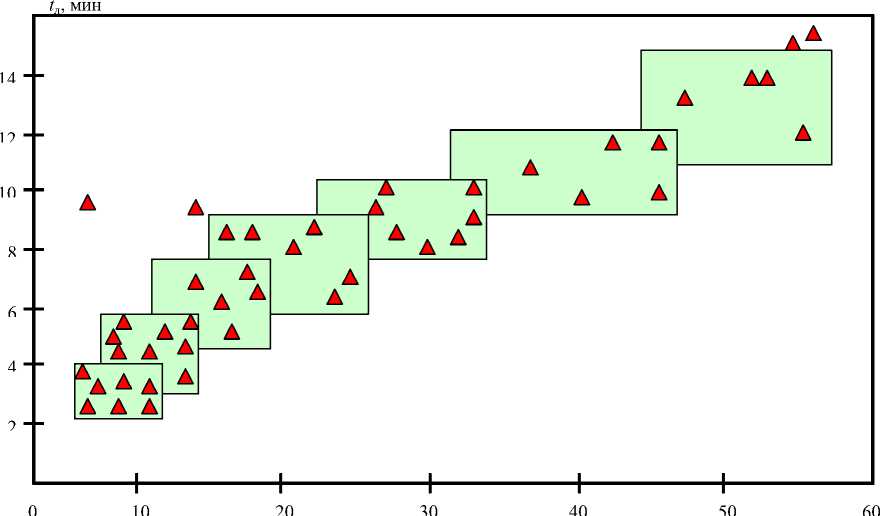
Масштаб аварии,

Рис. 1. Нечеткие множества, используемые для моделирования времени локализации (t л ) аварий по их масштабу.

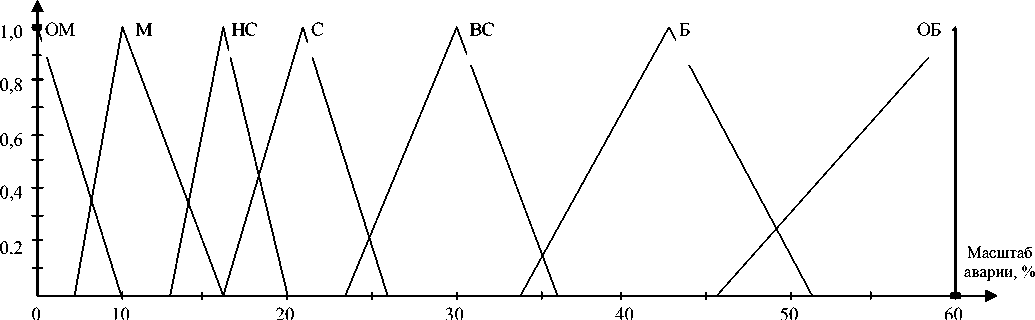
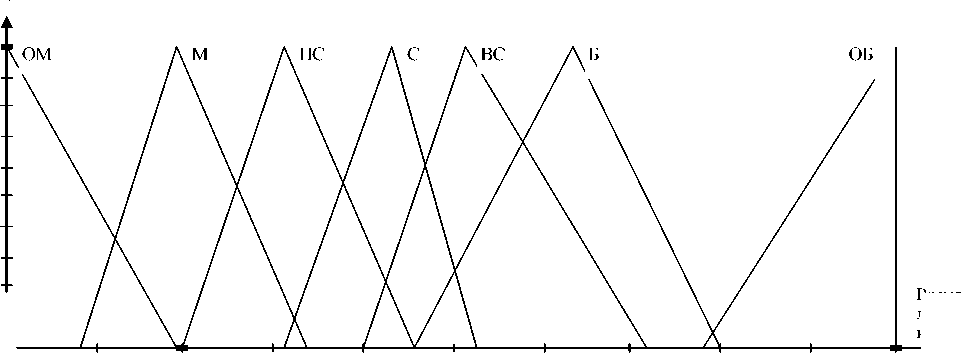
Переменный масштаб аварии является выходной нечеткой переменной величиной, а время локализации - выходной нечеткой переменной. Имена: очень малый (ОМ), малый (М), ниже среднего (НС), средний (С), выше среднего (ВС), большой (Б), очень большой (ОБ) - есть нечеткие множества. Функции принадлежности назначают каждой переменной степень принадлежности, изменяющуюся между 0 и 1. Функции принадлежности для нечетких множеств ОМ, М, С, ВС, Б, ОБ для масштаба аварий и времени их локализации приведены на рис. 2.

Нечеткая система работает в трех мерах: нечеткость, вывод и снятие нечеткости. Конкретная величина масштаба аварии может принадлежать всем нечетким множествам в некоторой степени. В зависимости от степеней принадлежности этим нечетким множествам инициируются все правила 1,2,...,7 частично или параллельно. Результатом являются нечеткое среднее взвешенное время локализации аварии, которое вычисляется как центроид пересекающихся областей треугольников, чьи веса изменяются в соответствии со степенями принадлежности каждому из нечетких множеств.

3,4

5,4

7,4

9,4

Рис. 2. Геометрическая интерпретация нечетких множеств ОМ, М, НС, С, ВС, Б, ОБ.

Время локализаци и аварии, р,

Нелинейное соотношение между временем локализации аварии и продолжительностью с момента ее возникновения с отопительной системой вагона может быть схвачено группированием рассеянных точек в частично перекрывающиеся области. Каждая область изображается нечетким правилом. Нечеткими правилами в этом случае являются следующие:

Правило 8. Если продолжительность времени с момента возникновения аварии меньше 15 минут (Ml5), тогда время локализации много меньше (ММ) резерва времени в аварийной ситуации.

Правило 9. Если продолжительность времени с момента возникновения аварии больше 15 минут (Б 15), тогда время ее локализации не близко (НБЛК) к резерву времени в аварийной ситуации.

Правило 10. Если продолжительность времени с момента возникновения аварии меньше 30 минут (МЗО), тогда время ее локализации в пределах (ВП) резерва времени в аварийной ситуации.

Правило 11. Если продолжительность времени с момента возникновения аварии близко к 30 минутам (БЛКЗО), тогда время ее локализации не выше (НВ) резерва времени в аварийной ситуации.

Правило 12. Если продолжительность времени с момента возникновения аварии больше 30 минут (БЗО), тогда время ее локализации не менее (НМ) резерва времени в аварийной ситуации.

Нечеткие правила были сформированы и для характеризации взаимосвязи между продолжительностью с момента возникновения аварий с отопительной системой и возможностью ее ликвидации без останова подвижного состава. Они имеют вид:

Правило 13. Если продолжительность с момента начала аварии меньше 15 минут (Ml5), тогда возможность ее ликвидации не ниже 0,95.

Правило 14. Если продолжительность с момента начала аварии больше 15 минут (Б15), тогда возможность ее ликвидации не выше 0,85.

Правило 15. Если продолжительность с момента начала аварии меньше 30 минут (МЗО), тогда возможность ее ликвидации выше (В) 0,75.

Правило 16. Если продолжительность с момента начала аварии близко к 30 минутам (БЛКЗО), тогда возможность ее ликвидации в пределах 0,7.

Правило 17. Если продолжительность с момента начала аварии больше минут (БЗО), тогда возможность ее ликвидации неизвестна.

Функции принадлежности для нечетких множеств, выделенных в скобках (см. правила 8 - 17), не могут быть сформированы как прежде. В этих правилах используются нечеткие отношения сравнения, такие как "много меньше...", "не близко к...", "в пределах...", "близко к...", "не выше (не более)...", "не ниже (не менее)...". Эти отношения сравнения можно выразить с помощью функций принадлежностей, имеющих аналитические описания в области приближенных рассуждений.

Обозначим через X = {х} множество базовых переменных с функцией принадлежности ц(х): X — > [0;1], ставящей в соответствие каждому элементу х0 g X число Цхо) из интервала [0;1]. Размытым множеством ~ полагаем совокупность пар вида (х, ц(х)), причем Х ={(х,ц(x))/хGХ}; ~~

ц (х):=Х ^ [0;1]. Учитывая, что объединение нечетких множеств ^{Х 1   Х 2} в Х

Ц ~ ~(х) = тахЦ ~(х), Ц ~(х)к х е Х имеют функцию принадлежности вида [ ]:  Х>иХ2       I Х1

~~ а пересечение нечетких множеств Х1 Х2 имеет функцию Ц ~ ~(х) = min Ц ~(х), Ц ~(х)кх е Х принадлежности вида [ ]:  Х 1иХ2       I Х1

Отношения сравнения выразим с помощью нечетких отношений, соответствующих вышеуказанным лингвистическим переменным: ' 1,0 < х < 0,02

Ц много меньше

log ₂ ( 2 - х ), 0.02 <  х <  1;

^ 0, х >  1

Ц ,   =1

много бол ьше

0,0 <  х <  1

2(1 - 2^{1 - х} ),1 <  х <  2;

1, х >  2

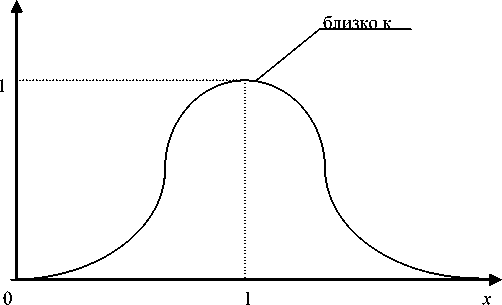
Ц бл изко к

' 1,0,98 <  х <  1,02

- 12( х - 1)² в противном случае e

Интервалы значений фактической продолжительности аварий "х" взяты как отношение их значений к 30 минутам для лингвистической переменной "близко к...".

Функцию принадлежности, соответствующую лингвистической переменной "не близко к...", определяем так:

И не близко к = max \ И много меньше , ^И много больше г

Интервалы значений фактического времени локализации аварий приняты соответствующими отношению их значений к определенному значению времени резерва при аварии для значений лингвистических переменных "много больше", "много меньше", "не близко к...". Тогда

получим:

1,0 <  х <  0,02    или   х >  2, И не близко к = 1 log2(2 - х ),0,02 <  x <  1;              (2) 2(1 - 21 - х ),1 <  х <  2.

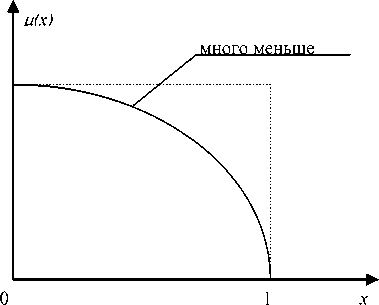
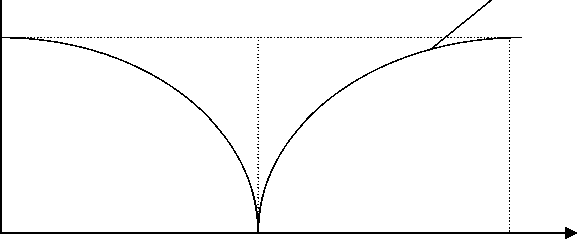
Графическое изображение функций принадлежностей приведено на рис.3., а их значения - в табл. 1.

1 L

не близко к

Их)

0                                  1                                2       х

Рис. 3. Функции принадлежности для переменных «много меньше», «близко к», «не близко к».

,                                                                      107

Таблица 1.

Табличное представление функций принадлежностей, соответствующих лингвистическим переменным "не близко к...", "близко к..."

Лингвистическая переменная
не близко к		близко к
х	ц^х)	х	Цк^х)
0,05	1,00	0,50	0,10
0,20	0,88	0,65	0,22
0,30	0,80	0,70	0,33
0,40	0,72	0,73	0,42
0,50	0,63	0,76	0,50
0,60	0,53	0,80	0,62
0,70	0,40	0,83	0,70
0,80	0,30	0,86	0,80
0,90	0,20	0,90	0,90
1,00	0	1,00	1,00
1,20	0,20	1,05	0,97
1,30	0,34	1,10	0,90
1,40	0,45	1,14	0,80
1,50	0,54	1,17	0,70
1,60	0,65	1,20	0,60
1,70	0,74	1,24	0,50
1,80	0,82	1,27	0,40
1,90	0,90	1,32	0,30
1,95	0,96	1,36	0,20
2,00	1,00	1,45	0,10

При сравнении времени локализации аварии и имеющегося резерва времени, одно из которых определено на интервале [а, в], возникают затруднения, поскольку сложно ответить на вопрос: на сколько больше одна из этих величин по сравнению с другой. В этом случае допустим, что функция принадлежности в крайних точках интервала [а, в] принимает наименьшее значение, а в середине интервала - наибольшее значение.

min ц ( x ) = £ , max ц ( x ) = 1

Пусть х          x        причем £ > 0 и ^ ^ 0. Графически такая функция имеет вид, представленный на рис. 4.4, из которого следует, что:

Ц( a) = Ц( b) = ^,

Ц

v

( a + b ^

2 )

= 1.

Такую функцию аналитически можно выразить в виде:

ц ( х ) = exp *

c I x

^“

a + b

>

где параметр "с" нужно подобрать так, чтобы выполнялось условие:

Ц ^(а) = Ц ^(Ь) = ^ .

Подставляя в (3) вместо х число "а ”, найдем значение параметра "с" : с = - 4 ln % / (a - b)²

Тогда функция ц (х) примет вид:

^ ( х ) в пределах = ехр

j4ln f ) ( a - b )²

x

—

a + b

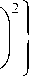
Значение функции ц(х) для случая "в пределах" в некоторых точках интервала [а, в] приведены в таблице 2. Использовать функцию вида (5) для лингвистических переменных "не выше", ине более", "не ниже", "не менее" нецелесообразно, так как в этих случаях должны выполняться условия:

для случая "не ниже", "не менее"

ц (а) = inf ^ (х); ^ (b) = 1, x e [a,b];

для случая "не выше", "не более"

ц (а) = 1; ^ (b) = inf ц (х), x e [a,b].

Таблица 2.

Значения функций принадлежностей для сравнения времени локализации аварии с отопительной системой и временем резерва, одно из которых определено в интервале [а, в], при ^ = 0,1

Значение х b - a (h =  12  )	Функция принадлежности
	в пределах	не выше, не более	не ниже, не менее
а	0,10	1,00	0,10
a+h	0,20	0,98	0,14
a+2h	0,36	0,94	0,20
a+3h=(a + b)/4	0,56	0,87	0,27
a+4h	0,80	0,80	0,36
a+5h	0,94	0,70	0,46
a+6h =(a + b)/2	1,00	0,56	0,50
a+7h	0,94	0,45	0,70
a+8h	0,80	0,36	0,80
a+9h	0,60	0,30	0,90
a+10h	0,40	0,20	0,94
a+11h	0,20	0,14	0,98
a+12h^b	0,10	0,10	1,00

По аналогии со случаем ив пределах" можно получить аналитические выражения функций принадлежностей для переменных "не выше", "не более", "не ниже", "не менее":

^ (х ) не выше, не более = ехр «

ln §

( b — a )²

■ ( x — a )² >

^ ( х ) не выше, не более = ехр<

ln §

( b — a )²

■ ( x — b )² >

• (6)

• (7)

Графические представления функций Ц_м выше, не более , Ц не ниже, не менее приведены на рис. 4, а их значения, в определенных точках интервала [а, в] (при § = 0,1) даны в таблице 2. В таблице 3 сведены значения функций принадлежностей для лингвистических переменных "меньше 15 минут", "больше 15 минут", "меньше 30 минут", "больше 30 минут".

Сравнения между результатами, полученными для двух типов данных, указывают, что масштаб аварий предпочтительнее, чем продолжительность с момента их возникновения. Среднеквадратические отклонения, рассчитанные по нечетким моделям данных от действительных соответственно составляют 8 - 10% и 13 - 16% при коэффициентах корреляции 0,94 и 0,87.

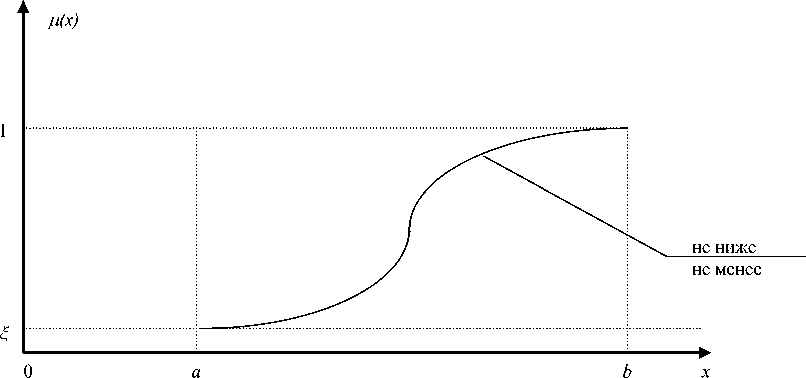
Ц (:х)

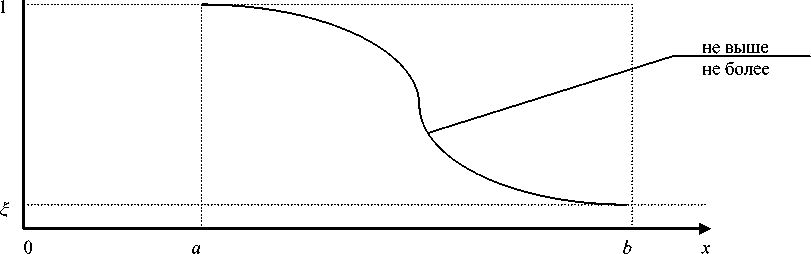
Рис. 4. Функции принадлежности для переменных «не ниже, не менее» и «не выше, не более».

Таблица 3.

Функции принадлежностей, соответствующие лингвистическим переменным "меньше 15 минут", "больше 15 минут", "меньше 30 минут", "больше 30 минут

Лингвистическая переменная				Значение функции принадлежности
меньше 15'	больше 15'	меньше 30'	больше 30'
минуты	минуты	минуты	минуты
1-3	15-26	1-15	60-65	1,0
1-4	15-25	16-30	55-65	0,9
1-5	15-24	20-30	50-60	0,8
1-6	15-23	21-30	30-55	0,7
1-7	15-22	22-30	30-53	0,6
1-8	15-21	23-30	30-50	0,5
1-9	15-20	24-30	30-45	0,4
1-10	15-19	25-30	30-43	0,3
1-12	15-18	26-30	30-40	0,2
1-13	15-17	27-30	30-35	0,1
1-14	15-16	28-30	30-33	0

Максимальные отклонения от фактических данных соответственно равны 20 и 25%. Это свидетельствует о достаточно высоких прогнозирующих способностях моделей. При этом с надежностью 0,90 гарантируется, что вероятность отклонения более, чем на 10% прогнозируемого значения от действительного по масштабной модели, не превысит значения 0,05. Таким образом масштаб аварий - лучший предсказатель времени их локализации.

Поэтому, учитывая общность закономерностей, присущих техногенным явлениям в предметных областях с неустойчивым гомеостазисом, на основании концепций знаний можно рекомендовать использование данных по масштабу аварий для оценки вероятности. Анализ также показал, что нечеткая модель дает улучшенные оценки времени локализации аварий по сравнению с моделями линейного регрессионного анализа (соответственно в среднем 10 и 35%) без существенного увеличения сложности модели. Графическая иллюстрация прямолинейной регрессионной модели, линейно-ломаной регрессионной модели и нечеткой модели представлена на рис. 5.

t _л, мин

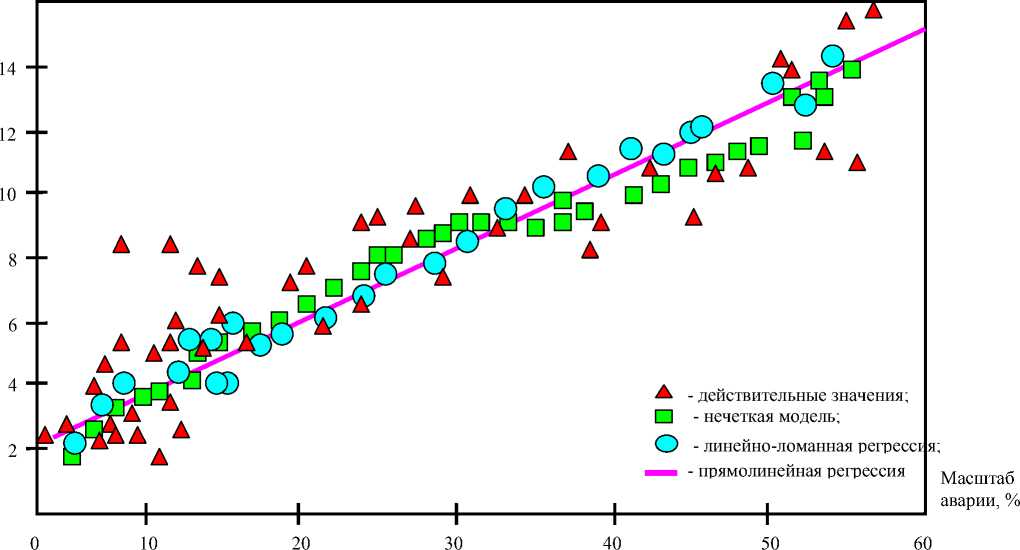
Рис. 5. Графическая иллюстрация различных

The indistinct forecasting model of time of localization of emergencies is considered and investigated at transportations. The recommended model provides quite satisfactory estimations of time of localization of emergencies. The analysis of results on duration from the moment of occurrence of failures and on their scale specifies in possibility of its application since the indistinct model well seizes a nonlinear parity between entrance and target variables.