Нечеткая нейросетевая кластеризация информационных ресурсов проектного репозитария

В настоящее время, в связи с геометрическим ростом информации, решение задач хранения, представления и информационного поиска электронных информационных ресурсов (ЭИР) является актуальной задачей, имеющей существенную научную и практическую ценность. Данная работа посвящена исследованию и разработки методов решения проблемы хранения и представления ЭИР. На данный момент хранение ЭИР различных архивов (в том числе и проектного репозитария) осуществляется ведением архива экспертом с использованием системы класса Enterprise Content Management systems (ECM) – системы управления информационными ресурсами предприятия. В российской практике ближе всего к понятию ECM находятся системы электронного документооборота.

При поддержке архива экспертом возникает ряд проблем: экспоненциальный рост количества ЭИР, субъективное разбиение ЭИР на категории, динамичность и дублирование информации. Использование систем ECM позволяет решить данные задачи, предлагая различную функциональность и технологичность для упрощения процесса и повышения качества хранения ЭИР. Данный вид систем позволяет значительно расширить возможности работ по управлению проектами и предлагает интеллектуальные средства для работы с ЭИР (анализу, хранению, поиску и представлению).

При исследовании рынка программного обеспечения, выявлено, что большинство систем (см. табл. 1) направлено на решение определенных задач: систематизация данных, классификация электронных ресурсов, управление электронными документами, управление потоками работ, поиск веб-ресурсов и т.п. При этом отсутствуют универсальные автоматизированные классификаторы, позволяющие систематизировать ЭИР по любому основанию.

Проблемная область проектного репозитария (архив документов ФНПЦ ОАО “НПО “МАРС”) представляет собой огромный массив документации, содержащий неструктурированные ЭИР, такие как положения, стандарты, инструкции, руководства, спецификации проектов и т.п. Поставлена задача расширить функционал программного средства автоматизации деятельности архивной службы ЭИР с целью интеллектуализации части процессов по управлению информацией. В частности, разработать и реализовать основу среды хранения ЭИР в виде нечеткого нейросетевого кластеризатора.

Здесь формальная постановка задачи кластеризации заключается в следующем.

Пусть X — множество объектов, Z — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами с(x, x'). Имеется конечная обучающая выборка объектов Xl = {x1, . . . , xl} ⊂ X . Требуется разбить выборку на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике с , а объекты разных кластеров существенно отличались. При этом каждому объекту xi ∈ Xl приписывается метка (номер) кластера zi .

Алгоритм кластеризации – это функция a: X>Z , которая любому объекту x ∈ X ставит в соответствие метку кластера z ∈ Z .

Решение задачи кластеризации ЭИР проектного репозитария выдвигает ряд требований к алгоритму кластеризации:

отсутствие обучающей выборки;

применимость сильносгруппированных данных;

автоматическое определение оптимального числа кластеров;

не более чем логолинейный рост времени работы кластеризатора с увеличением количества текстов;

минимальная (в лучшем случае отсутствующая) настройка со стороны пользователя.

Таблица 1. Программные продукты, реализующие задачи систем ECM

Задача кластеризации текстов с трудом поддается формализации. Оценка адекватности разбиения ЭИР на кластеры, как правило, основывается на мнении эксперта и трудно выразима в виде какой-то одной численной характеристики. Возникает требование интерпретируемости результата, т.е. кластерам должны быть присвоены некоторые метки, отражающие их семантику. Следовательно, процедура кластеризации должна еще обладать свойством:

интерпретируемость найденных кластеров в терминах смысла содержания относящихся к ним документов.

На практике зачастую оказывается, что задаче кластеризации данных свойственна нечеткость, значительно затрудняющая или вообще делающая невозможным получение решения. Очень сложно установить точное числовое значение порога принадлежности ЭИР к какому-либо кластеру, легче установить меру близости рассматриваемого ЭИР к кластеру. Из данного условия следует, если можно установить меру близости ЭИР к одному кластеру, то можно установить и к другим. Возникает еще два требования к методу кластеризации:

разбиение информационных ресурсов на кластеры с нечеткими границами;

возможности отнесения документа более чем к одному кластеру.

Рассмотрим более подробно распространенные алгоритмы кластеризации, где кластерный анализ занимает одно из центральных мест среди методов анализа данных и представляет собой совокупность методов, подходов и процедур, разработанных для решения проблемы формирования однородных классов (кластеров) в произвольной проблемной области.

В самом общем виде методы кластеризации могут быть разбиты на две группы: представляющие тексты в виде векторов в многомерном пространстве признаков (и использующие метрику близости между векторами) и методы, использующие другие представления анализируемых текстов.

Первая представлена алгоритмами иерархической кластеризации (Single/Complete/Average Link), неиерархическими алгоритмами (методы ближайшего соседа – модификация k-means, FCM, нейронные сети SOM, ART и т.д.) а также большим числом других базирующихся на них методов.

Примерами алгоритмов второй группы является алгоритм Suffix Trie Clustering (STC – древовидные структуры). Недостатки метода STC – обязательное наличие первоначального дерева, значительное время работы при больших размерах первоначального дерева.

Неиерархические методы выявляют более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых переменных в набор, участвующий в кластеризации. Но при этом в большинстве алгоритмах необходимо заранее определить количество кластеров, количество итераций или правило остановки, а также некоторые другие параметры кластеризации.

Иерархические методы строят полное дерево вложенных кластеров. Сложности данных методов кластеризации: ограничение объема набора данных; выбор меры близости; негибкость полученных классификаций.

В ходе анализа приведенных выше алгоритмов кластеризации выявлено, что максимально соответствует требованиям к алгоритму кластеризации ЭИР метод нейронных сетей SOM (самоорганизующиеся карты Кохонена):

Таблица 2. Применимость методов к кластеризации ЭИР

Название	Метод	U5 Н 8 - g g & 5 а ч я S S Ри	- о S я я -Q Щ s ° " Л Я н я и я О д я Я Я s 3 с Я Я	св & Щ О в 2 у Ю О S у S	Я 3 Св О С Щ  Св  CQ 6 н ° н 8 « св у Ч $ § Я О и 2	S щ св и Д-S S Ю щ		hQ м Он
Условия		+	+	-	-	+	+	-
Метод ближайшего соседа (К-ближайших) [1],[5]	Неиерархический метод, стабилизация центроида	+/-	-/+	-	+	-	-	-
Байбесовские сети доверия[1]	Направленный ациклический граф	+	+/-	-	-	-	+	+
FCM-метод [4]	Неиерархический метод, нечеткое разбиение	+	+	-	+	-/+	+	+
Сети Кохонена [2]	Нейронная сеть	+	+	-	-	-/+	-/+	-
Нейронная сеть Хопфилда [6]	Нейронная сеть	+	+/-	+	-	-	-	+
Single Link, Complete Link, Group Average [1]	Агломеративный иерархический метод	+	-	-	-	-	-	-
Suffix Tree Clustering (STC) [1]	Суффиксное дерево	+	+	+	-	-	-	-

определяет автоматически количество получаемых кластеров (является самоорганизующейся системой);

не требует наличия обучаемой выборки (используется метод обучения без учителя);

применима к сильно сгруппированным данным (позволяет настраивать параметры сети для более “тонкого” разбиения);

дает возможность настроить параметры сети по умолчанию (все характеристики, влияющие на результат работы нейронной сети параметризованы и установлены по умолчанию для стандартного решения);

увеличение количества текстов не влечет за собой экспоненциальный рост времени обработки (время обработки зависит от размерности словаря словоформ);

интерпретация найденных кластеров осуществляется осмысленно в ключевых словах (входы представляют собой вектор частот встречаемости слов ЭИР, на выходе классы, описываемые ключевыми словами);

возможно реализовать нечеткую интерпретацию результата путем добавления слоя, реализующего нечеткую систему вывода.

Для построения среды хранения на основе нейронной сети Кохонена необходимо модифицировать выбранную нейронную сеть в соответ- ствии с применимостью к кластеризации ЭИР проектного репозитария, надстроить слой нейронной сети в виде системы нечеткого вывода.

Задача индексирования ЭИР заключается в том, что входным вектором X системы кластерного анализа ЭИР является результат индексирования – частотный портрет документа. В процессе индексирования ЭИР автоматически извлекается индекс в виде вектора основных понятий и их связи с весовыми характеристиками [3]. В качестве смыслового портрета текста рассматривается сеть понятий — множество ключевых слов или словосочетаний. Каждое понятие имеет некоторый вес, отражающий значимость этого понятия в тексте.

Для первоначальной оценки важности дескриптора используется алгоритмы:

• 1.    Частота дескриптора основывается на простом приравнивании веса термина к его частоте появления в тексте (TF – term frequency):

• 2.    Мера TFIDF является произведением двух сомножителей: TF и IDF.

tf_i = freq ( x_i ).

Данный показатель малозначителен в общем случае. Поэтому в случае, когда доступна статистика использования термов во всем информационном массиве, более эффективно вычисление TFIDF.

TF = tf /tf_max , где tf — частота слова в документе; tf_max — максимальная частота слова в документе;

IDF (inverse document frequency — обратная частота документа) — инверсия частоты, с которой некоторое слово встречается в документах коллекции. Учёт IDF уменьшает вес широко употребительных слов.

IDF = log -D-, di c ti где D — количество документов в выборке, di c ti - количество документов, в которых встречается дескриптор ti.

Большой вес в TF-IDF получат слова с высокой частотой в пределах конкретного документа и с низкой частотой употреблений в других документах.

Для отслеживания динамика зависимости результатов работы метода кластеризации от полноты, точности представления дескриптором значений документов ЭИР в ходе экспериментов используются оба способа расчета дескриптора ЭИР.

Нейронная сеть Кохонена, использующая метод обучения без учителя (unsupervised learning) – это самоорганизующиеся карты Ко-хонена (Self-Organizing Map – SOM).

Сеть SOM позволяют осуществить отображение входного n-мерного пространства в выходное m -мерное, то есть [ F : R" ^ R m ] . Процесс обучения характеризуется самообучением, выполняемым без учителя на основе образов, поступающих на нейроны сети. В качестве метода обучения используется конкурентное обучение. Сеть SOM (см. рис. 1) состоит из двух слоев.

Первый слой состоит из N обрабатывающих элементов (число которых соответствует размерности векторов признаков), каждый из которых получает n входных сигналов x 1 , x ₂ ,..., x_n . Входу x_i и связи ( i,j ) приписывается вес w_ij . Данный слой выполняет распределительные функции. Каждый нейрон первого слоя имеет соединение со всеми нейронными элементами второго (или выходного) слоя.

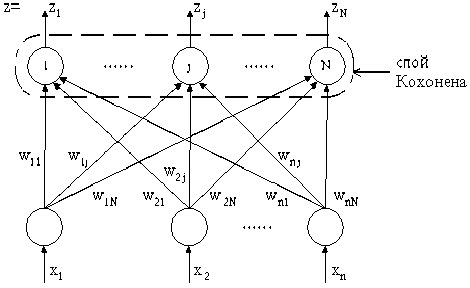
Рис. 1. Структура сети SOM

Второй слой (называемый также слоем Ко-хонена) осуществляет конкуренцию между нейронными элементами, в результате которого определяется нейрон-победитель. Выходные элементы называются кластерными. Весовые значения кластерного элемента интерпретируются как значения координат, описывающих позицию кластера в пространстве входных данных.

Каждый обрабатывающий элемент слоя Ко-хонена подсчитывает свою входную интенсивность I_j в соответствии с формулой:

Ij= D (Wj, X), где Wj = (w1 j,..., wj)T и X = (x 1,...,xn) ; D (Wj, X) - некоторая мера (метрика) расстояния между Wj и Х.

В качестве меры сходства векторов чаще всего используют:

• 1)    Эвклидово расстояние: d(W,X) = || W — X |.

• 2)    Сферическое дуговое расстояние:

A(W, X) = 1 — W Т X = 1 — cos0, где W Т X – скалярное произведение.

Угол между векторам v и w высчитывается следующим образом:

cos

v • w

и м м j

Нормы или модули векторов вычисляются по формулам:

llvll = _Л/v, ² + + v ^{2 2} + + w ²

• 1    ... , 1 ... ” .

При разработке модифицированной нейронной сети Кохонена для кластеризации ЭИР решено использовать эвклидово расстояние d (W, X ) .

Обучающие данные для слоя Кохонена предположительно состоят из последовательности входных векторов {Х}, которые извлекаются случайно с фиксированной плотностью распределения вероятностей. Как только очередной из векторов Х вводится в сеть, обрабатывающие элементы Кохонена начинают соревноваться между собой, чтобы найти победителя, для которого достигается min d (X, W.). Тогда для победив-jj

*

шего нейрона j выход устанавливается z_j , а для всех остальных Z j , j Ф j . В этот момент происходит изменение весов в соответствии с законом обучения Кохонена.

Представим работу алгоритма SOM пошагово: Шаг 1. Вектор Х подается на вход сети.

Шаг 2. Определяются расстояния D(W j , X ) между Х и весовыми векторами W j каждого нейрона по формуле:

Di = E(x- - w^j, где хi – компонента i входного вектора X, wij – вес входа i нейрона j.

Шаг 3. Нейрон, который имеет весовой вектор, самый близкий к X , объявляется победителем. Этот весовой вектор, называемый Wc, становится основным в группе весовых векторов, которые лежат в пределах расстояния D от Wc , так называемой области активации нейрона-победителя.

Шаг 4. Определение весов нейронов внутри области активации по формуле:

W j (t + 1) = W j ( t ) + a [ X - W j ( t )] , где a – норма обучения, 0 – номер итерации.

Шаг 5. Повторяются шаги с 1 по 4 для каждого входного вектора.

Очевидно, что при таком обучении весовой вектор W _j движется к входному вектору Х . В течение первых 1000 итераций, норма обучения должна быть около единицы a - 1 . Затем по мере обучения уменьшается до величины a=0,1 . Характер уменьшения нормы обучения не имеет особого значения, может быть линейным, экспоненциальным или обратно-пропорциональным числу итераций.

В результате прошедшая обучение сеть может использоваться для классификации неизвестных объектов на основе их сходства с объектами, предъявленными сети в процессе обучения. Классификация выполняется посредством подачи на вход сети испытуемого вектора, вычисления возбуждения для каждого нейрона с последующим выбором нейрона с наивысшим возбуждением как индикатора правильной классификации. Если рассматривать классификацию пошагово, то алгоритм кластеризации остается без изменений, только опускается шаг 4.

Таким образом, сеть SOM имеет набор входных элементов (частотные портреты ЭИР), и набор выходных элементов (множество кластеров). Обучение нейронной сети происходит на каждом документе. Интерпретация полученных кластеров осуществляется осмысленно в ключевых словах, поскольку нейронная сеть Кохоне-на представляет весовые значения кластерного элемента как значения координат, описывающих позицию кластера в пространстве входных данных. Следовательно, на полученное пространство кластеров и объектов можно описать в виде нечетких отношений (меры близости).

Система нечеткого логического вывода, основой которой является проведение операции нечеткого логического вывода или это база пра- вил, содержащая нечеткие высказывания в форме ‘Если-то’ и функции принадлежности для соответствующих лингвистических термов.

Пусть в базе правил имеется m правил вида:

R 1 : ЕСЛИ x 1 это A 11 ...И... x n это A 1 n , ТО у это B 1

R i : ЕСЛИ x 1 это A 1 ...И... x n это A 1 n , ТО у это B_i

R :ЕСЛИ это A …И…x это A ,ТО y m                  1            -1            n mn , это Bm , где xk , k=1..n – входные переменные; y – выходная переменная; Aik – заданные нечеткие множества с функциями принадлежности.

Результатом нечеткого вывода является четкое значение переменной y* на основе заданных четких значений x_k , k=1..n.

В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (см. рис. 2).

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.

Полученная в результате работы сети SOM система мер близости кластеров и объектов ЭИР позволяет использовать нечеткий логический вывод по алгоритму Сугено (иногда говорят алгоритм Такаги-Сугено).

Нечеткий вывод Сугено выполняется по нечеткой базе знаний:

\ (                  ^

U11x = a,jpc весом wjp I ^ y=bj,o+ •••+bj,n • xn, j=1 V i=1                                 / где bj,i - некоторые числа.

Рассмотрим алгоритм нечеткого логического вывода по Сугено пошагово:

Шаг 1. Фазификация. Определяются степени истинности, то есть значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как A ik ( x_k ) , i=1..m,k=1..n . Ц j _P ( x k ) - функция принадлежности входа x i нечеткому терму a i , j _p , то есть:

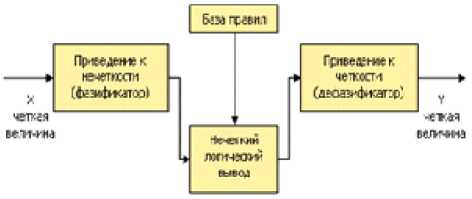
Рис. 2. Структура нечеткого логического вывода xi ai, jp = J ^jp(xi)/ xi , x i e x, xi ].

xi

Шаг 2. Нечеткий вывод. Заключения правил d j задаются не нечеткими термами, а линейной функцией от входов: dj = bj. 0 + E bj i • xi .

i = 1 n

Правила в базе знаний Сугено являются своего рода переключателями с одного линейного закона “входы - выход” на другой, тоже линейный. Границы подобластей размытые, следовательно, одновременно могут выполняться несколько линейных законов, но с различными степенями. Степени принадлежности входного вектора X к значениям d _j рассчитывается следующим образом:

^{p d (} X ) =        w •. " I ^p - ⁽ x i ¹ 1 _;

p=1, kj       i =1 n              j = 1 , m ’ где v (л) - операция из s-нормы (t-нормы), т.е. из множества реализаций логической операций ИЛИ (И). В нечетком логическом выводе Суге-но наиболее часто используются следующие реализации треугольных норм: вероятностное ИЛИ как s-норма и произведение как t-норма.

Шаг 3. Композиция. В результате получаем такое нечеткое множество у , соответствующее входному вектору X :

у P d i ( X ) p d ₂( X ) p d m ( X ) ...

d l d 2 d m .

Приведенное выше нечеткое множество является обычным нечетким множеством первого порядка. Оно задано на множестве четких чисел.

Шаг 4. Дефазификация. Результирующее значение выхода y определяется как суперпозиция линейных зависимостей, выполняемых в данной точке X*n мерного факторного пространства. Для этого дефазифицируют нечеткое множество у , находя взвешенное среднее:

У =

^ Pdj( X) • dj j=1, m___________________

E P d j ( X )

j = 1 m

Для разрабатываемой модели было определено несколько объектных переменных и для них найдены функции принадлежности.

Функция принадлежности p ( bff ) определяет объектную переменную “тип класса”, где базовое значение b=[0;1] и нечеткие значения F = {плотный, средний, разреженный}.

Переменная b представляет собой коэффициент плотности класса p и рассчитывается следующим образом:

P =

У max min /

n

где rmax, rmin – расстояния, максимально и минимально удаленного от центра класса объекта (ЭИР); n – количество объектов рассматриваемого класса.

Функция принадлежности p ( bfj ) представлена 3 функциями, каждая из которых описывает одно нечеткое значение:

Z – функция для значения “плотный”;

PI – функция для “средний”;

S – функция для “разреженный”.

Другая функция принадлежности p ( b ff ) определяет расстояние объекта до класса, где b=[0;1] и F = {центр, близко, граница, недалеко, далеко}.

База правил состоит из набора 15 правил. Приведем несколько из них:

Если x 1 = “плотный” и x ₂ =“центр”, то у = “в классе”

Если x 1 = “плотный” и x ₂ = “близко”, то у = “граница класса”

Если x 1 = “средний” и x ₂ = “центр”, то у = “в центре класса”

Если x ₁ = “средний” и x ₂ = “близко”, то у = “в классе”

Если x ₁ = “разреженный” и x ₂ = “близко”, то y = “в центре классе”.

Таким образом, система нечеткого логического вывода определяет меру близости объектов ЭИР и полученных классов как нечеткое значение, которое позволяет оперировать лингвистическими переменными естественного языка.

Модуль нечеткой кластеризации представляет собой отдельный модуль программного обеспечения “Интеллектуальный сетевой архив ЭИР” архивной службы, предназначенный для разбивки массива ЭИР на классы на основе частотных портретов, полученных в процессе работы модуля “Индексатор”. Программное обеспечение реализовано средствами JDK 6 (Java SE Development Kit) в свободнораспространяемой среде разработки NetBeans 6.1.

В программном продукте “Кластеризатор G_SOM 2.0” реализован модифицированный алгоритм нейронной сети Кохонена и система нечеткого логического вывода Сугено. Кластери-затор позволяет пользователю выполнить следующие действия:

интерактивно настроить параметры подключения и подключиться к базе данных;

• интерактивно изменить параметры нейронной сети;

  

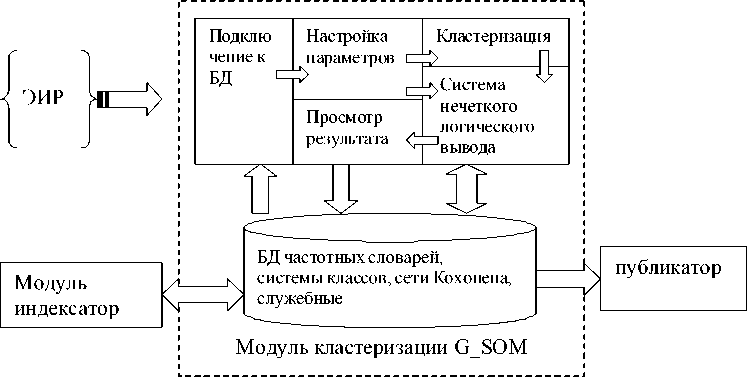
  Рис. 3. Работа программного обеспечения “Интеллектуального сетевого архива ЭИР”

  
  

запустить процесс кластеризации (четкой или нечеткой);

получить матрицу результатов (столбцы кластеры, поля документы, на пересечении проставляется мера близости в виде четких и нечетких значений);

сохранить полученный результат в базе данных или в файле.

Таким образом, нечеткий нейросетевой кла-стеризатор на основе SOM прост в реализации, удобен в обучении, требует минимального участия эксперта, а так же позволяет выбирать оптимальное соотношение точность/полнота результата разбиения ЭИР на классы за счет настройки параметров нейронной сети и системы нечеткого логического вывода. При этом результаты работы сети SOM могут быть выражены не только числовыми значениями, но и нечеткими, то есть на естественном языке.