Нечеткие кластеры с объемными прототипами в тематической обработке данных дистанционного зондирования Земли

алистичную визуализацию трехмерных сцен участков леса. Кроме того, достаточно точное моделирование растительности по данным лазерного сканирования позволяет рассчитывать статистические характеристики биомассы и морфометрические показатели.

Существует несколько алгоритмов моделирования растительности. Наиболее часто применяемые на практике – это использование грамматик L- систем и алгоритма Space Colonization [16-20].

Материалы и методы

Моделирование растительности в трехмерном пространстве (3D) включает в себя как процесс создания трехмерной модели отдельно стоящего дерева, так и моделирование лесной сцены, в которой необходимо учитывать взаимовлияние объектов - деревьев друг на друга. Дерево является основным объектом изучения в силу присущей ему сложной структуры ветвления (моноподиальный, симподиальный и тернарный) у различных пород деревьев. Кустарники рассматриваются как частный случай дерева с тернарным типом ветвления без выраженного ствола.

При рассмотрении существующих подходов к моделированию отдельно стоящих деревьев можно выделить три основные из них:

• -    полигональное моделирование ( polygon-based modelling );

• -    моделирование на основе изображений объекта (image-based modelling );

  – моделирование на основе шаблона/эскиза модели ( sketch-based modeling ) [9, 19, 21].

В последнее время все большую популярность начинают приобретать методы построения трехмерных объектов с помощью вокселей. По сути, воксель является полным аналогом пикселя в 3D. Пиксель (pixel - англ. picture element ) - элемент изображения, воксель ( voxel - англ. volume element ) - элемент объёма. Практически все характеристики пикселя переносятся на воксель, учитывая размерность. Воксель – это элемент объёмного изображения, содержащего значение элемента в трёхмерном пространстве. Как и в случае с пикселами, сами по себе вокселы не содержат информации о координатах в пространстве. Координаты вычисляются из их позиции в трёхмерной матрице - структуре, моделирующей объёмный объект или поле значений параметра в трёхмерном пространстве.

Воксельные модели имеют определённое разрешение. Для хранения воксельной модели применяют массив размерами X х Y х Z . Несжатые воксельные модели (по сравнению с векторными) требуют гораздо больший объем машинной памяти при обработке, поэтому распространение получили сжатые воксельные модели, принцип которых основан на использовании разреженного воксельного октодерева. Сравнение полигонального и воксельного представления моделей показано в таблице 1.

Каждый элемент разряженного воксельного октодерева имеет либо 8 потомков, либо не имеет потомков вовсе. Узел дерева – куб, полностью содержащий в себе объект. При этом 8 потомков каждого куба (октанты) - это кубы, полученные делением его пополам в каждой плоскости, таким образом, каждый новый слой всё более «уточняет» предыдущий (рис. 1).

В качестве значения вокселя в общем случае может выступать любой параметр, включая цвет. В нашем случае, в качестве значения вокселя выступает плотность точек лазерного сканирования. Что касается формы вокселя, то в общем случае воксели могут быть в виде куба

Таблица 1. Сравнительная характеристика полигональной и воксельной графики

Table 1. Comparative characteristics of polygonal and voxel graphics

Описание	Полигональная графика	Воксельная графика
	Метод представления объектов в виде набора многоугольников	Метод представления в виде набора трехмерных объектов – вокселей
Достоинства	Программно и аппаратно развитая технология. Использование ресурсов видеокарты. Относительно малые затраты памяти. Варьирование уровня детализации	Представление внутренней структуры. Для реалистичного отображения не требуется вспомогательных средств. Большие возможности изменения объектов
Недостатки	Необходимость использовать шейдеры для реалистичного отображения мелких деталей. Отсутствует внутренняя структура. Сложности с преломлением света и подобными эффектами. Статичность моделей	Значительные требования к памяти. Более низкое качество изображения. Привязка точек к узлам матрицы. Одинаковый уровень детализации. Отсутствие развитых аппаратных средств

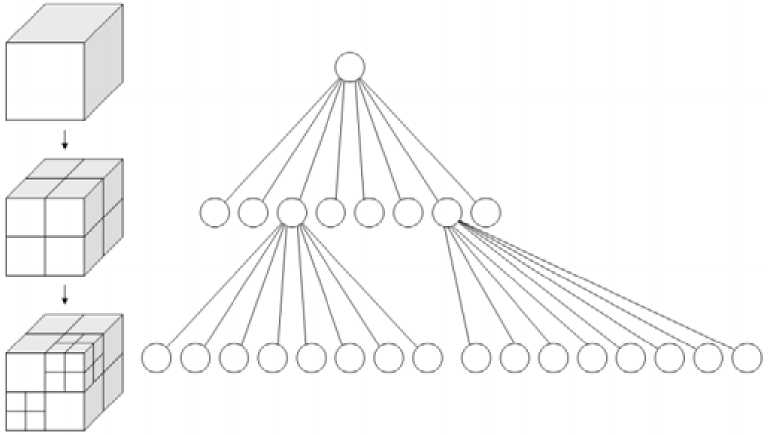
Рис. 1. Соответствие разделения куба на октанты со структурой октодерева

Fig 1. The compliance division of a cube into octants with the structure of oktotree или шара, чаще всего встречается кубическое представление, как частный случай параллелепипеда.

В работе представлены воксели в виде кубов для упрощения и удобства работы, где P min – координата нижнего левого угла вокселя, P_max – координата верхнего правого угла вокселя (рис. 2).

Координат воксели не хранят, они вычисляются из относительного расположения вокселя. Таким образом, воксели используются для представления трёхмерных объектов.

Широкое применение воксели нашли в медицине, в частности в компьютерной томографии. Изображения большого количества рентгеновских или ультразвуковых снимков под

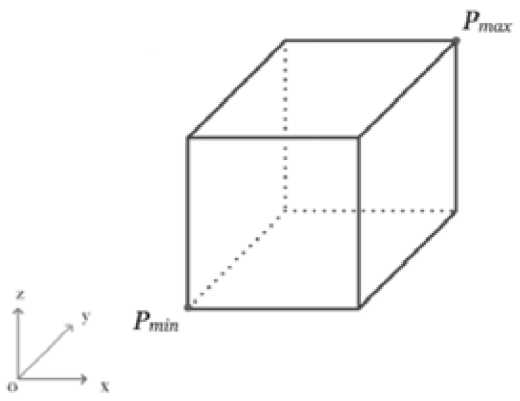
Рис. 2. Представление воксела в трехмерном пространстве

Fig. 2. Representation of the voxel in three-dimensional space

абвг

Рис. 3. Общая схема моделирования трехмерной сцены с помощью вокселей: а – исходное облако точек данных лазерного сканирования; б - составление трехмерных карт высот по исходным данным; в – отображение полученных результатов; г – сохранение модели

Fig. 3. General modeling scheme of the three-dimensional scene using voxels: а – the original point cloud data laser scanning; б – preparation of three-dimensional height maps for the source data; в – display of received results; г – save the model разными углами (порядка 100–200 снимков) обрабатываются, и создается трехмерный массив плотностей различных участков тканей исследуемого органа. Этот массив представляет собой «объемную картину», элементом которой является воксель. Второе, более наглядное, применение вокселей - компьютерные игры. Схема предложенного метода восстановления ландшафтных сцен в общем виде состоит из четырех этапов:

• –    получение исходного облака точек, включая стандартную предобработку данных;

• –    построение трехмерной карты высот по исходным данным;

• –    отображение полученных результатов;

• –    визуализация и сохранение конечной модели ландшафта (рис. 3).

• 1    этап. Получение исходного облака точек, включая стандартную предобработку данных – фильтрацию от шумов и совмещение данных в единую систему координат – данные задачи решаются аппаратной частью большинства лазерных систем.

• 2    этап. Построение трехмерной карты высот по исходным данным. Существует несколько наиболее распространенных способов цифрового представления рельефа в виде:

• -    векторных линий (горизонталей или иных изолиний с равным или неравным шагом);

• -    регулярной матрицы (регулярная или матричная модель) высот земной поверхности (представление на регулярной сетке квадратов, прямоугольников или треугольников, когда в ее узлах заданы значения высоты); далее по тексту для этого вида используются наименования «регулярная матрица высот» или «регулярная модель» (GRID).

По способу вычисления значения уровней поля между узлами сетки различают решеточные и ячеистые сетки. В первой из них такие значения интерполируются по значениям высот в соседних точках, вторая модель рассматривает точки как центры ячеек с постоянным значением отметки высоты. В программной реализации карта высот чаще всего представляется в виде двумерного массива переменных с плавающей точкой – набора значений высот для каждого значения в определенном интервале x, z на плоскости, лежащей горизонтально.

• 3    этап. Отображение полученных результатов. Для воксельных моделей существует множество способов визуализации: Splatting, Marching cubes, Ray tracing, Maximum intensity projection . Один из быстрейших способов называется «бросанием снежков» (англ. splatting ). Вокселы «бросаются» на поверхность просмотра в порядке удалённости от неё, от дальних к близким. Получившиеся «следы от снежков» отображаются как диски, цвет и прозрачность которых изменяются в зависимости от диаметра, в соответствии с нормальным (гауссовым) распределением. В различных реализациях могут использоваться другие элементы или же другие распределения.

Для улучшения качества изображения используются более сложные алгоритмы построения геометрии сцены: алгоритм Marching cubes и другие. Алгоритм Marching Cubes (бегущие кубики) строит изоповерхность, опираясь на данные вокселов. Обычная реализация алгоритма использует значения 8 соседних вокселов, чтобы отрисовать полигон внутри куба, образованного их координатами. Так как существует всего 256 возможных комбинаций, можно заранее их подготовить и использовать типовые «кирпичики» (уже в экранных координатах) для от-рисовки больших объёмов данных в хорошем качестве визуализации.

Ray tracing - технология построения изображения, при которой отслеживается обратная траектория распространения луча (от экрана к источнику). Вероятность попадания луча в какой-нибудь сегмент сцены - пропорциональна площади этого сегмента. Чем больше примитивов содержится в участке сцены – тем больше пересечений нужно будет просчитывать при попадании луча в этот сегмент.

Существуют и другие алгоритмы, например, проекция максимальной интенсивности, которая хорошо отображает положение в трёхмерном пространстве наиболее ярких участков трёхмерного объекта. В целом аналогично Ray tracing луч проходит сквозь объект и выбирается воксель с максимальным значением.

Результаты и их обсуждение

Результатом воздушного лазерного сканирования является трехмерное облако точек в единой системе координат. Все регистрируемые лазером точки переводятся в новую воксель-ную систему координат по следующим формулам:

r = Int ( x — x min ) + 1,

Ai c Int(y Лmin^+1

Z — Z • l = Int (i) + 1, A Ik где i, j, k - координаты воксела; функция Int - функция округления до ближайшего целого числа; ∆i, ∆j, ∆k – размерность воксела. Т. к. используется кубическое представление вокселов, то Ai = Aj = Ak = р. Матрица перехода M от координат (x, y, z) к воксельному пространству (r, c, l):

Г1  0 0 - * 1 pp M = 1 0 - Рр 0 ^° _ 0   0   1   6 где x0, y0 - координаты верхнего левого угла пространства точек лазерного сканирования (рис. 4).

Построение карты высот выполняется с наложением сетки G на исходное облако точек. Существует два вид сеток: регулярная сетка (триангулярная, квадратная и др. сетки) и адаптивная сетка. В случае адаптации необходимо учитывать, что применение высоких уровней адаптации приводит к ухудшению масштабируемости задачи. При подборе размера ячеек следует принимать во внимание, что на характерные размеры в задаче (диаметр ствола и диаметр кроны дерева) должно приходиться минимум 4 ячейки, а лучше 8–10.

Решение реализуется на регулярной разностной сетке, т. е. расчетная область разбивается на ячейки с шагом hr вдоль оси r на K частей, с шагом hl вдоль оси l на M частей и с шагом hc вдоль оси c на N частей. Ячейки сетки имеют вид прямоугольных параллелепипедов, и определяются тремя индексами (k, m, n). В каждой ячейке вычисляется центр масс (kc, mc, nc), координаты которого записываются в отдельный массив данных, который визуализируется, остальные точки ячейки отбрасываются при построении исходного облака точек.

Для визуализации ландшафта используется алгоритм Ray tracing, по которому выполняет- ся перемещение по лучу с некоторым шагом и находится пересечение с вокселем, при этом, на каждом шаге проводится трехлинейная интерполяция, где 8 вершин представляют середины

Рис. 4. Переход к воксельной системе координат

Fig. 4. The transition to the voxel coordinate system соседних вокселей. На CPU используется окто-дерево в качестве оптимальной структуры для быстрого пропуска прозрачных вокселей. На GPU для 3D-текстуры трехлинейная интерполяция выполняется автоматически средствами видеокарты. На GPU не используется окто-дерево для пропуска прозрачных пикселей, поскольку в случае 3D-текстуры иногда оказывается, что быстрее учитывать все воксели, чем тратить время на поиск и пропуск прозрачных. В качестве модели освещения используется затенение по Фонгу (рис. 5).

Основные показатели, характеризующие количественно процесс моделирования – требуемый объем памяти и скорость визуализации, представлены в таблице 2.

Данный алгоритм предоставляет возможность изменения яркости и цвета поверхностных вокселей, позволяет визуализировать различные природные эффекты – туман, дождь, снег, путем изменения цвета и яркости поверхностных вокселей, полученных при отражении луча. Значение расстояния от камеры до точки пересечения луча с объектом сцены используется для моделирования тумана: чем дальше объект находится от камеры, тем меньше интенсивность его цвета (для расчетов используется экспоненциальная функция убывания интенсивности) (рис. 6).

Дальнейшим шагом при создании реалистичной лесной сцены является наполнение этой сцены моделями растительности – деревьями и кустарниками.

Для индивидуального моделирования каждого из объектов массива растительности следует выделить подмножество точек отдельного объекта дерева из исходного облака точек. Наиболее сложной задачей является отделение соседних объектов при их близком расположении друг с другом (перекрытии крон соседних деревьев). Решается данный вопрос путем определения слоя (значение по оси с является постоянной величиной и принадлежит некоторому интер-

Рис. 5. Модель поверхности ландшафта размерности 8096 × 8096 × 256 вокселей

Fig 5. The surface model of the landscape dimension 8096 × 8096 × 256 voxels

Таблица 2. Показатели визуализации ландшафта по алгоритму Ray tracing

Table 2. Indicators of landscape rendering in Ray tracing algorithm

Вид 1	Размер, Мб	Миллион лучей, сек
	90.265	104.252
Вид 2	71.806	164.275
Вид 3	64.539	117.941

б

Рис. 6. Визуализация природных эффектов: а – исходная сцена; б – наложение снежного покрова; в – наложение тумана

Fig. 6. Rendering of natural effects: а – initial stage; б – overlay of snow cover; в – the imposition of fog

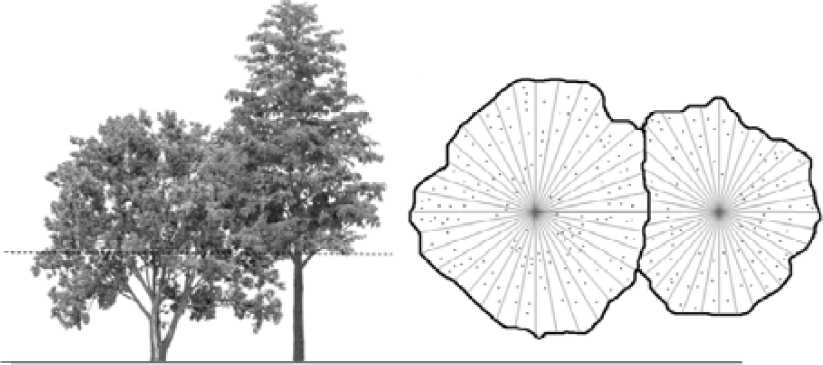
Рис. 7. Вычисление центра масс дерева для слоя с максимальным количеством точек лазерного сканирования

Fig. 7. The calculation of the center of mass of the tree for the layer with the maximum number of points of laser scanning валу равному 5–6 размерам высоты воксела, принятого в сцене) с максимальным количеством точек (рис. 7).

Для каждой области вычисляется центр масс, проекция которого на поверхность смоделированного ранее ландшафта является корнем дерева.

В последующем, имея облако точек, относящееся к одному объекту, выполняется моделирование структуры ветвления на основе алгоритма Space Colonization . Данный алгоритм изначально был предложен А. Рунионом с соавторами [16] для предсказания движения человека в толпе, и позже стал использоваться для визуализации различных ветвящихся структур.

Основная идея заключается в итеративном добавлении новых элементов (ветвей) к существующей геометрической структуре объекта (дерева), сформированного на предыдущих шагах. Данный алгоритм является адаптивным, т. е. процесс роста зависит от следующих параметров: близлежащее присутствие объектов окружающего мира, соседство с другими деревьями.

Допустим имеется некоторая «корневая» точка v, из этой точки может выходить несколько ветвей, т. е. в окрестности данной точки имеется множество точек S (г), находящихся на рас-– 735 – стоянии меньшем, чем di – параметр, задаваемый пользователем (параметр управления). Если множество S (v) не пустое, то новая точка v’ присоединяется к общей структуре дерева путем построения сегмента (v, v’). Причем новая точка v’ находится на расстоянии D от исходной точки v в направлении средненормированного вектора по отношению ко всем источникам SeS (v).

Данный алгоритм использовался для детальной прорисовки кроны дерева. На рисунке 8 а показана визуализация исходного облака точек (фрагмент), на рисунке 8 б отображено разбиение пространства облака точек на вокселы, на рисунке 8 в для каждого воксела определен центр масс. Полученное облако точек является исходным облаком для работы алгоритма Space Colonization , а на рисунке 8 г представлена работа правил ветвления на основе L -систем (около трех итераций).

Конечные позиции работы правил ветвления L -систем являются стартовыми точками работы алгоритма Space Colonization . Каждая последующая ветвь вычисляется следующим образом:

v' = v + DU, где D – расстояние между точками v и v’, v (x, y, z) – точка начала новой ветви, v’ (x’, y’, z) - конечная точка новой ветви, тг - средненормированный вектор направления роста ветви:

„ т ^т = Цп|| £ s e₅(v)^ .

Данный процесс завершается при прохождении всех точек кроны дерева или при выполнении заданного пользователем количества итераций. Некоторые узловые точки удаляются. Это называется «прореживанием», иными словами при построении нового сегмента происходит проверка: все точки, находящиеся на расстоянии dk ( dk – kill distance , входной параметр) от точки v ’, удаляются.

Рис. 8. Алгоритм процесса роста дерева: а – исходное облако точек лазерного сканирования; б – разбиение на множество вокселов; в – определение центра масс в каждом вокселе; г – работа алгоритма Space Colonization

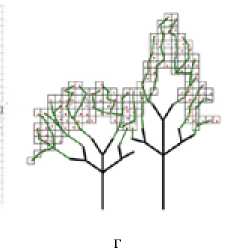
Fig 8. The algorithm of the tree growth process: а – the original point cloud laser scanning; б – tiling set of voxels; в – definition of center of mass in each voxel; г –the work of the Space Colonization algorithm

а

б

в

Рис. 9. Моделирования кроны дерева в трехмерном пространстве: а – выделение объема из исходного облака точек; б – моделирование ветвей; в – моделирование лиственной массы

• Fig. 9.    Modeling crown of the tree in three-dimensional space: а – allocations of original point cloud; б – the modeling of branches; в – the modeling of foliage mass

а

б

в

Рис. 10. Результаты трехмерного моделирования лесной ландшафтной сцены: а – исходное облако лазерных точек; б – локализация крон деревьев; в – интегрированная трехмерная модель лесной ландшафтной сцены

• Fig. 10.    Results of the three-dimensional modeling of forest landscape scenes: a – the original cloud of laser points; б – location of tree crowns; в – integrated three-dimensional model of forest landscape scene

Процесс моделирования кроны дерева представлен на рис. 9.

Основным результатом является трехмерная модель участка леса, представленная на рисунке 10. На рисунке 10 а представлена визуализация данных лазерного сканирования в виде исходного облака точек трехмерных данных, на рисунке 10 б отображены результаты процесса локализации и диаметра крон деревьев, на рисунке 10 в представлена трехмерная модель лесной ландшафтной сцены с использованием графических примитивов в качестве представления крон деревьев.

Заключение

Использование воксельного трехмерного представления дает возможность моделировать лесные ландшафтные сцены по точкам лазерного сканирования с необходимой точностью для – 737 – каждого типа возникающих задач. Одним из достоинств воксельного представления графики является снятие ограничений на геометрическую сложность сцены – единственным и универсальным фактором, влияющим на сложность моделируемых объектов, является воксельное разрешение.

Использование алгоритма Ray Tracing позволяет получать реалистичные модели лесных ландшафтных сцен. Вместе с тем, следует отметить недостаток данного алгоритма – необходимость в просчете пересечения луча со всеми примитивами в сцене, что является довольно ресурсоемкой процедурой. Преимуществом данного подхода является возможность добавления различных природных эффектов в сцену путем изменения яркости и цвета «поверхностных» вокселей без дополнительных перерасчетов в сцене. Для построения залесенного участка земной поверхности размерностью 8096 × 8096 × 256 вокселей требуется не более 10 Мб машинной памяти. При этом, для прорисовки геометрии крон и стовлов отдельных деревьев рекомендуется использовать алгоритм Space Colonization .