Нечеткий контроллер для модернизации тормозной системы самолета Ил-76

Тормозная система воздушного судна – сложная высокотехнологическая структура, которая совместно с другими взлетно-посадочными механизмами и системами обеспечивает торможение воздушного судна. Тормозная система работает с огромными скоростями и нагрузками при максимально возможном весе и размерах воздушного судна, поэтому к ней предъявляется достаточно серьезные требования. При рассмотрении тормозной системы, применяемой в военнотранспортной авиации, в частности, в самолете Ил-76, можно сказать, что используется достаточно надежная классическая схема, состоящая из гидравлической и механической части.

На самолете Ил-76 управление тормозами колес главных ног шасси осуществляется тормозными подножками педалей руля направления с места правого или левого летчиков. Правая подножка затормаживает все колеса правых ног, а левая подножка – левых ног, тормозной момент пропорционален ходу тормозных подножек. Установленные в системе антиюзовой автоматики двухинтегральные автоматы торможения сбрасывают давление из тормозных цилиндров при возникновении углового замедления колес, превышающего допустимую величину (в момент, предшествующий юзу), а также при падении числа оборотов ниже допустимых пределов. Давление сбрасывается одновременно из тормозных цилиндров двух колес, расположенных симметрично относительно оси ноги.

Применение в тормозной системе Ил-76 антиюзовой автоматики позволяет сократить тормозное расстояние, пройденное воздушным судном по взлетно-посадочной полосе в зависимости от сцепной способности опорной поверхности, тем не менее, необходима дальнейшая модернизация антиблокировочной системы с целью повышения эффективности торможения и уменьшения износа авиационной шины.

Постановка задачи

Одним из вариантов модернизации антиюзовой автоматики в рамках тормозной системы является применение электронной вычислительной техники, которая, в свою очередь, осуществляет управление тормозными моментами на колесах на основе большего количества внешних параметров и факторов.

Существуют проблемы, связанные с построением автоматических систем управления тормозным моментом и его распределением на колесах на базе цифровой техники с учетом особенностей рабочих процессов систем и агрегатов воздушного судна. Выбор рациональной структуры, параметров и построение алгоритмов функционирования таких систем, включающих множество элементов, работа которых основана на различных физических принципах, связаны со значительными трудностями. При модернизации антиюзовой системы необходим учет особенностей функционирования каждого элемента в отдельности и процессов их взаимодействия и взаимовлияния при движении воздушного судна по взлетно-посадочной полосе.

Для модернизации антиюзовой системы необходимы теоретические исследования комплекса «автоматическая система управления – самолет – внешняя среда» с использованием математического моделирования рабочих процессов на электронно-вычислительной машине. Вышеприведенные обстоятельства требуют проведения углубленных исследований процессов, происходящих в тормозной системе. В связи с этим задача определения и исследования закономерностей приложения тормозного момента к колесу, его распределения между колесами и разработка на их основе алгоритма управления, влияющего на повышение эффективности торможения, является весьма актуальной.

Вариант решения

Для разработки алгоритма работы антиюзовой системы по растормаживанию колес (приложению тормозного момента) предлагается применить нечеткую систему управления в связи с тем, что до соприкосновения колеса с взлетно-посадочной полосой часть параметров будет неизвестна. При решении задачи необходимо описать лингвистические переменные, которые будут поступать в цифровом сигнале с датчиков на аналого-цифровой преобразователь (АЦП); функции их принадлежности; стратегию управления посредством нечетких правил, которые можно объединить в единую базу правил или знаний о системе. Создание алгоритма необходимо проводить на основе CASE-технологии, которая позволяет все действия выполнять только посредством общения с экраном электронно-вычислительной машины, не заглядывая в программный код.

На стадии offline-оптимизации проверяется работоспособность созданной системы, чтобы в дальнейшем на этапе online-оптимизации разработать систему управления, в которой все ее элементы, в частности, исполнительные механизмы и элементы регистрирующего комплекса соединены физической линией связи. Такой вид отладки позволяет наблюдать поведение системы в реальных условиях и при необходимости вносить изменения в систему управления.

На этапе реализации получаем окончательный вариант кода для конкретного микроконтроллера и, если нужно, связываем его с основной программой. Основу программного кода составляет ядро, аппаратно-ориентированное на конкретный тип процессора. В результате после посту-пенчатой проработки всей методики разработки алгоритма получим нечеткий алгоритм распределения тормозных моментов.

Особенностями нечеткого управления являются возможность представления техники и знаний о посадке, которыми обладает летчик, с помощью лингвистических правил управления (ЛПУ), что позволяет обойтись без количественной модели объекта управления. Поэтому в качестве устройства управления с функциями адаптации к изменениям параметров, характеризующих взаимодействие колеса с опорной поверхностью взлетно-посадочной полосы, разработан нечеткий контроллер (НК), который построен на основе качественных соотношений между частотой вращения колеса и его подтормаживанием, т. е. правил и знаний управления. В НК выполняются нечеткие выводы, следуя правилам управления, и вычисляются задающая величина, причем в качестве входной информации для НК используются отклонение частоты вращения.

Для повышения робастности системы управления ограничением тормозного момента спроектирован НК с функцией обучения. Это означает, что параметры НК настраиваются в реальном времени или итеративно по результатам оценки реакций на управляющие воздействия. Инфор-

Системы навигации и управления… мация о замеряемых параметрах воздушного судна в виде напряжения с датчиков поступает в АЦП, который преобразует их в цифровые данные, понятные программному обеспечению электронно-вычислительной машины. Затем на основе нечетких ЛПУ с использованием нечеткого вывода вычисляем задающую величину, которая через цифроаналоговый преобразователь (ЦАП) поступает на исполнительный механизм.

Следуя [1], будем использовать в НК следующие лингвистические правила управления (ЛПУ):

ЛПУ 1: если е_к есть Р₁, то Ди_к есть Р_м1;

ЛПУ 2: если е_к есть N₁, то Ди_к есть N_M1;

ЛПУ 3: если Дек есть Р2,то Дик есть Рм2;                                              (1)

ЛПУ 4: если Де к есть N₂, то Ди к есть N _m2 ;

ЛПУ 5: если Д²е_к есть Р₃, то Ди_к есть Р_м3;

ЛПУ 6: если Д²е_к есть N₃, то Ди_к есть N_M3.

Здесь для момента времени k : е_k = r – у_k ; Δ е_k = е_k – е_{k –1} (разность отклонений 1-го порядка); Δ ²е k = Δ е k – Δ е k –1 , (разность отклонений 2-го порядка); Δ u k = u k – Δ u k –1 (приращение задающей величины); r , у k – заданная и текущая скорости самолета соответственно; P , N – положительное и отрицательное значения.

При нечетком управлении, благодаря нечеткому выводу, задающая величина определяется путем установления компромисса между правилами, приводящими к таким противоположным действиям.

Если сравнить эти правила с ПИДК (ПИД-контроллер), то можно заметить, что ЛПУ 1 и ЛПУ 2 соответствуют интегральному, ЛПУ 3 и ЛПУ 4 – пропорциональному, ЛПУ 5 и ЛПУ 6 – дифференциальному воздействиям. Однако обработка правил выполняется с помощью нечетких выводов, и в результате будет построен нелинейный ПИДК.

Величины Р i , P ui , N i , N ui ( i = 1, 2, 3), входящие в правила, представляют собой нечеткие множества, которые имеют функции принадлежности для каждой переменной (рис. 1).

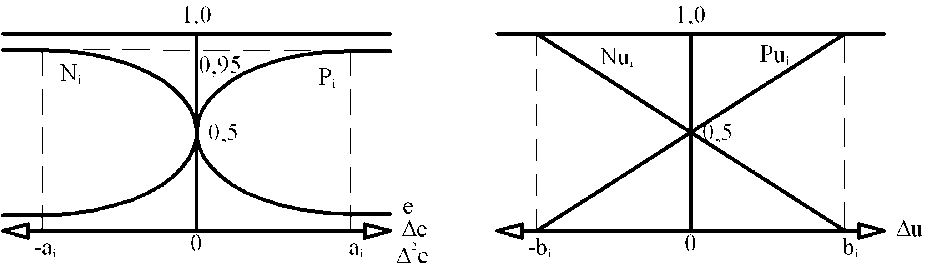
а)                                                              б)

Рис. 1. Функции принадлежности: а – предпосылка; б – заключение

Функции принадлежности предпосылок имеют вид арктангенсов, а функции принадлежности заключений – прямых линий. Представление предпосылки в виде кривой с насыщением необходимо для того, чтобы усиление контроллера при почти нулевом отклонении от заданной величины было большим, а если отклонение будет возрастать, то происходило бы насыщение усиления. Благодаря этому задающую величину ограничиваем даже при вводе в контроллер очень больших ошибочных данных. Важным аспектом, связанным со структурой НК, является определение параметров а i , b i ( i = 1, 2, 3) функций принадлежностей.

Для нечеткого вывода используем формулы на основе сложных правил косвенного метода, предложенного Цукамото [2]. Нечеткий вывод представляем следующей формулой:

Предпосылка 1: если е_к есть Р-^то Ди_к есть Р_М1 (ЛПУ1)

Предпосылка 2: е к есть Р‘                                                        (2)

Заключение Ди к есть С₁

Здесь Р' и С1 – нечеткие (лингвистические) переменные. Смысл этой формулы заключается в том, что при задании нечеткого словного предложения предпосылки 1 и Р' в качестве нечеткого входного значения определяется заключение (нечеткое выходное значение) С1.

Нечеткий вывод может быть прямым, когда значение принадлежности нечеткого множества трактуется как значение истинности, а вывод осуществляется с использованием этого значения, или косвенным, когда вывод осуществляется с использованием нечеткого (лингвистического) значения истинности, полученного в результате нечеткого представления значения истинности.

Для определения обратного значения истинности используем нечеткое правило «модус по-ненс».

По нечеткому тезису « е_k это Р ₁» предпосылки 1 и нечеткому тезису « е_k это Р' » предпосылки 2 в формуле (2) определяется нечеткое множество степени истинности « е k это Р 1 », т. е. нечеткое значение истинности т _Р . Иначе говоря, определяется т Р такое, что « е_к есть Р 1 » есть т _Р ^ « е_к есть Р' » (это называют определением обратного значения истинности). Нечеткое множество определяем следующей формулой:

Н т _{Р 1} (^и) = Н р '( м Р (^и) ) , ое [ ^0,1 ] .                                                                       ⁽³⁾

Нечеткий «модус поненс» предназначен для вывода степени истинности заключения «А и_к есть Р_{и 1}» или нечеткого значения истинности т_Р по заданным степени истинности т_Р ,_Р

Р и 1                                                        P 1 ^ P u 1

(нечеткого значения истинности) нечеткого условного предложения (записывается как Р 1 ^ Р_и 1 задается в виде

Р1 ^ Ри 1 = 1 ^ - Р1 + Ри 1 ), Р1, Ри 1 G[0,1] , где p1, pu1 – числовые значения истинности.

С помощью этой формулы представляем нечеткое значение истинности т р ^ р нечеткого условного предложения Р₁ ^ Р_{и 1} следующим образом:

тР1^Ри 1 = 1 Л (1 - тР1 + тРи 1) , где «+» и «–» – это нечеткие операции, определенные по принципу расширения.

Используя множество α-уровней для нечеткого значения истинности в формуле (5), получаем та .Р = 1 л(1 -та +та к

Р1^ Ри 1                Р1 Ри 1 , где та={t| цт(t)>а}, ае[0,1].

Отсюда следует, что при заданных т р ^ _Р (обычно предполагается истинным) и т _Р значение т _Р определяем, решив уравнение (6). Если величина т _Р нормализована (высота равна 1) и выпукла, а т р ^ _Р очень мала в диапазоне [0, 1], записываем т Р = [ а₁ ( а ) , а 2 ( а ) ] , т _Р ^ _Р = [ r ( а ) ,1 ] , поэтому величину т Р _; определяем из следующей формулы:

^т Р_{и 1} = [ { a 1 ( ^а ) ^{+ r} ( ^а ) ^{- 1} } ^v 0,¹ ] .                                                                         (7)

По полученному с помощью «модус поненс» нечеткому значению истинности т _Р ] заключения «Δ u_k есть Р_{u 1}» и нечеткому множеству заключений Р_{u 1} определяем нечеткое множество С ₁ заключений «А и_к если C ₁» с помощью «А и_к есть Р_{и 1}» есть т_Р ^ «А и_к есть C ₁» (это называют оп-

Р u 1 ределением значения истинности).

Нечеткое множество C ₁ определяем следующим выражением:

Н с₁ ( А ^и _к ) = Р^т р_{и 1} ( р р ₁ ( А ^и _к ) ) .                                                                            ⁽8)

Используя вышенаписанные определения, определим нечеткое множество C 1 задающих величин Δ u k для случая, когда относительно отклонения е k от заданного значения имеется нечеткая информация. Аналогично определяем ц с. ( i = 2 ^ 6 ) для ЛПУ 2-ЛПУ 6. Функция принадлежности С величины Δ u k при объединении правил находится с помощью формулы

Ц с ( ^{А и}к ) = min Н с ( ^{А и}к ) .                                                                   ⁽⁹⁾

i

Системы навигации и управления…

Однако, поскольку на выходе контроллера необходимо получить четкое значение, в качестве задающей величины определяем значение, удовлетворяющее следующему выражению:

Н С ( a u k ) = Sup ц C i ( A u k ) , A U k e U

где U – полное множество задающих величин.

На практике при проектировании НК системы управления тормозными моментами к колесу в качестве входной информации используем четкие значения. Задающую величину A u k для этого случая находим следующим образом:

Н pA ei) = ¹ arctg ( d i • ed + 0,^5,

‘           П1                       i = 1,2,3.(11)

Н N ( e i ) = - arctg (^- d i • e i ) + 0,5,

I i n

Пусть е1 = е, е2 = Δе, е3 = Δ2е. Функция принадлежности предпосылки (см. рис. 1) для е имеет вид, где di = tg(0,45π)/ai, i = 1, 2, 3.(12)

Функция принадлежности заключения имеет вид:

ц Pu 1(AU ) = 2b AU + 0,5, <                1            i = 1,2,3.(13)

НN (Au) = -—Au + 0,5, 12

С помощью процедур 1–3 нечеткого вывода определяем нечеткое множество С задающих величин (рис. 2) [3]. Таким образом, если точки пересечения Δu1, Δu2, Δu3 всех функций принад- лежности выразить в виде

^A u = ¹ { arctg ( d 1 e k ) + arctg ( d 2 ^A e k ) } / ( 5 1 + g 2 ) , n

A u 2 = n { arctg ( d 2 A e k ) + arctg ( d 3 A ² e k ) } / ( g 2 + g 3 ) , i = 1,2,3.

Au 3 = n{arctg (d3A 2 ek) + arctg (d1 ek)} / (53 + 51), где gi = 1/(2bi), i = 1, 2, 3, то

A u_k = medium { A u 1 , A u ₂, A u 3 } , где medium означает среднее значение.

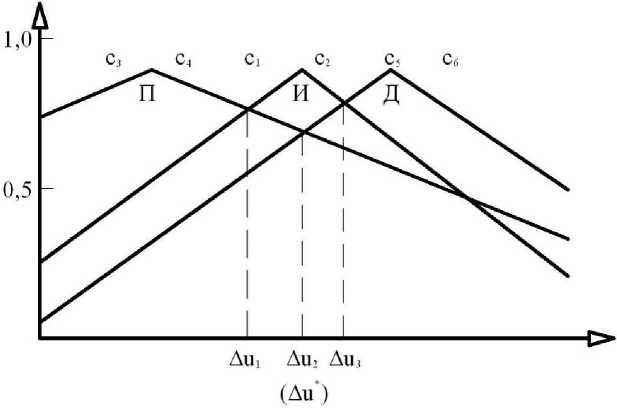
Рис. 2. Функция принадлежности задающей величины

Задающая величина А и * , полученная из формул (14) и (15), выражена двумя линейными связями относительно arctg ( d 1 e k ) , arctg ( d 2 А e_k ) и arctg ( d 3 А 2 e_k ) , а относительно e_k , A e_k и A² e_k - нелинейной связью. Поэтому считаем, что НК – это нелинейный ПИД-контроллер [4].

Выводы

Разработана методика формирования алгоритма управления тормозным моментом на основе принципов нечеткой логики, включающая этапы описания системы; оffline-оптимизации; оnline-оптимизации и реализации. Обоснованы лингвистические переменные для реализации нечеткого контроллера, описываемые арктангенциальными и S-функциями принадлежности. Разработанная методика рекомендуется при проектировании тормозной (антиюзовой) системы в военнотранспортной авиации.