Нечеткий логический вывод в системе управления беспилотного летательного аппарата

Широкое применение беспилотных летательных аппаратов (БПЛА) в дистанционном зондировании земной поверхности, в том числе в экологическом мониторинге, повышает требования к навигационному обеспечению полета, точности определения географических координат объектов и системам автономного управления БПЛА. Применение БПЛА наряду с зондированием земной поверхности с помощью космических аппаратов позволяет проводить более детальное и оперативное исследование биологического разнообразия особо охраняемых территорий. Системы автономного управления являются ядром обеспечения качества получаемой с борта БПЛА информации для формирования информационного обеспечения задач экологического мониторинга особо охраняемых территорий [1].

Самым распространенным методом анализа и синтеза алгоритмов управления объектами является «обычная» линеаризация, основанная на разложении нелинейной функции в окрестностях точки, определяющей заданный режим, в ряд Тейлора и отбрасывании нелинейных членов. Такая линеаризация заменяет исходную нелинейную модель приближенной линейной моделью и обладает рядом недостатков [2].

Если нелинейность сложного объекта управления существенна, то для решения задач синтеза алгоритмов управления используют методы нелинейной теории управления. Одним из эффективных подходов для компенсации влияния нелинейностей в системе управления объектом является метод линеаризации обратной связью (ЛОС). Данный метод позволяет перейти от нелинейной системы к линейной путем преобразования, включающего преобразование обратной связью, в результате чего получается система, эквивалентная исходной. Однако применение метода ЛОС зависит от точной априорной информации о динамике объекта управления. Для устранения этого недостатка предполагается использовать ЛОС совместно с нечеткими системами логического вывода.

Системы нечеткого логического вывода обладают хорошими аппроксимирующими свойствами и служат универсальными аппроксиматорами любой нелинейной функции. Данные свойства нечетких систем позволяют применять их для решения задач в области автономного адаптивного управления. В частности, предполагается использовать нечеткие системы при проектировании систем автоматического управления беспилотных летательных аппаратов (БПЛА).

Для решения задачи адаптивного управления свойство адаптации достигается, чаще всего, посредством формирования в явном или неявном виде математической модели объекта или воздействия на него. При широких изменениях параметров объекта управления стационарная эталонная модель системы становится неприемлемой для решения задачи управления БПЛА для различных режимов полета. Для решения данной проблемы предполагается построение адаптивной эталонной модели с идентификацией, которая оценивает неизвестные параметры БПЛА. Применение нечеткой логики и адаптивных принципов построения систем управления позволяет существенно снизить влияние неопределенности на качество систем управления, компенсируя недостаток априорной информации на этапе проектирования систем.

Нечеткий аппроксиматор

Рассмотрим нечеткую систему, у которой есть пять основных частей: фаззификатор, нечеткая база знаний, функции принадлежности, ядро нечеткого логического вывода, дефаззи-фикатор.

Нечеткие правила, известные так же, как база знаний, содержат качественную и эвристическую информацию в виде ( Если - То ) правил. Данные правила имеют следующую форму:

R j : ЕсЛи^ есть A*, x 2 есть A²,..., x n есть A " ^Toz есть B ,           (1)

где j = 1,2,... N — номер ^{нечеткого} правила; [ x i, x ₂,..., x n ] ^T = X e U c R N ; z e V c R — переменные входа и выхода соответственно; Aⁱ_j и B_j - нечеткие функции принадлежности.

В данной статье будем использовать гауссову функцию принадлежности, которая имеет следующую формулу:

д (х)=exp

x

x

a

где σ - параметр крутизны функции; x указывает положение функции.

Ядро нечеткого логического вывода на основе правил базы знаний определяет значение выходной переменной в виде нечеткого множества B с функцией принадлежности

H B ( z ) = ц_А _ R ( X,z ), соответствующего нечеткому значению входной переменной множества A’ с функцией принадлежности H a ( x ), где знак «◦» - максминная композиция.

В конце при дефаззификации нечеткого множества B с функцией принадлежности д . ( z )

^B получаем четкое значение переменной z е V с R , которая является выходной переменной нечеткой системы. Для получения числового значения выходной переменной на заключительном этапе нечеткого логического вывода используются следующие методы: «центр тяжести», «взвешенного среднего», «центр площади», «максимум», «средний центр». Чаще всего используют метод центра тяжести.

Так, для нечеткого логического вывода по синглтонной базе знаний выход нечеткой модели с использованием метода центра тяжести будет описываться следующим уравнением:

Nn

X ® j ⁽ t )⁽П_!=А - ^{( х} - ))

F ( * - * j-_fn.    ₍ \     W ( t ) G ( ' ),                (²)

^ХП - = 1 ^ A j ⁽ x i ) = 1

где ю ( , ) - весовые функции, определяющие п о ложение     ., ) на оси, W = _to( t Х « ,< t       ⁽ t )],

П n мДx i )

5 n > ._; « )

Рассмотрим теперь наиболее важное свойство нечеткой системы. Как показано в [3, 4], у нечеткой системы логического вывода есть много общего с нейронными сетями. Как нейронная сеть, которая имеет хорошие способности к обучению и аппроксимирующие свойства, нечеткая система логического вывода с гауссовыми функциями принадлежности способна к сколь угодно точной аппроксимации нелинейной функции на множестве U. Следующая теорема теоретически подтверждает это.

Теорема 1 [3]. Для каждой вещественной непрерывной функции f, заданной на компакте U е R , и для произвольного £ >0 существует нечеткая система, формирующая выходную функцию F *(X) = W*TG(X) такую, что supllf (X) - F (X)||< е .                                    (3)

Будем использовать нечеткий аппроксиматор, чтобы определить функцию f ( x ), далее f_x . Согласно теореме 1, обозначим f x = W' G f как оптимальный аппроксиматор неизвестной функции f_x , где G_f – определяемая функция.

При этом известна небольшая положительная величина s f такая, что ошибка аппроксимации

* εf = fx fx удовлетворят соотношению

= . 1^ = ;

Обозначим так же пока неизвестный оптимальный вектор W* в нечетком аппроксиматоре, f как его оценку, тогда получим:

nput vmat* "X*"

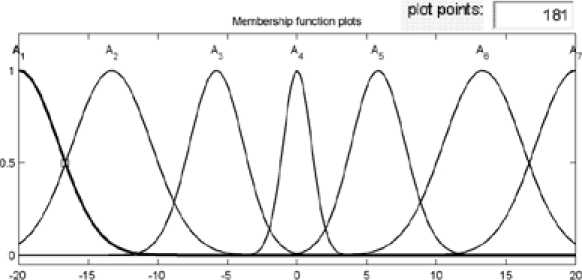
Рис. 1. Функции принадлежности

f X = W f T G_f -

Чтобы аппроксимировать функцию f x , понадобятся нечеткие правила вида (1) с нечеткими функциями принадлежности, изображенными на рис. 1.

Настройка оценки вектора W f T в f X будет осуществляться по формуле

W f T = W XL -0 T G x ,                                    (4)

T где 0, = 0 f > 0 - коэффициент адаптации, обычно экспериментально выбираемый пара-ff метр.

С^{огласно} рис. ¹ начальная позиция базы данных, которая настраивается адаптивным законом (3), определяется как W fT ^- [-20-13^-6 ^{0 6} 13 20], коэффициент адаптации ⁰ , установим равным 0,3 Е , где ^ - единичная матрица размером j х j .

Метод линеаризации обратной связью и нечеткие системы логического вывода

Рассмотрим использование ЛОС и систем нечеткого логического вывода в структуре адаптивной системы управления полетом БПЛА.

Рассмотрим нелинейную систему вида x = f (x) + g (x) u x e R" u e R

(4а)

где f ( x ), g ( x ) - гладкие векторные функции. Начало координат при нулевом управлении является положением равновесия: f (0) = 0. Данная система может быть записана в виде

(4б)

z = Az + bu,

"0 1 0 . . 0" Г 0 ^ 0 0 1 . . 0 где A = ... 0 ... 0 ... . 0 .. .1 b = ... 0 Z - T (x) L о 0 0 .. . 1. ч 1 v влетворяющее уравнению u = а(x) + в(x)и.

диффеоморфизм, и - новое управление, удо-

Модель обратного преобразования --- -._   — — — —      =   — — — ——

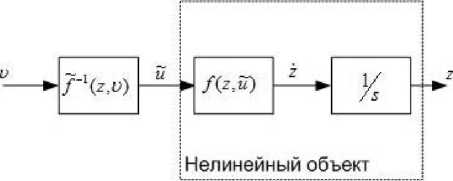
Рис. 2. Приближенная модель обратного преобразования

Для формирования управления необходимо осуществить обратное преобразование функции z = T(x) с обратной связью u = а(x) + в(x)и, т.е. вычислить x = T-1(z) в режиме реального времени. Однако данная функция известна приближенно, значит, функция (4б) фактически имеетвид z = Az + bu + А,

~ ~ где А = f (z, и) - f (z, и) - ошибка обратного преобразования, f (z, u) - аппроксимация обрат -ного преобразования. Приближенная модель обратного преобразования представлена на рис. 2.

Таким образом, когда обратное преобразование основано на приближенной модели объекта управления, что чаще всего происходит, то система управления дополняется элементом компенсации ошибок обратного преобразования при применении метода ЛОС.

В реальной системе управления ДПЛА такую процедуру возможно осуществить с помощью алгоритма сигнальной адаптации. Для этого в систему вводится сигнал u ad (t ), который суммируется с сигналом линейного регулятора u₀ ( t ), в результате получаем сигнал на входе объекта управления:

и ( t ) = и о( t ) + U ad ( t ) .                                                         (5)

При таком подходе формирования адаптивного управления требуется для каждого канала управления введение отдельного адаптивного элемента.

Архитектура адаптивного управления с использованием обратного преобразования при применении метода ЛОС изображена на рис. 3.

При применении нечеткого логического вывода (фаззиконтроллера) для формирования в (5) адаптивного управления сигнал u_ad(t ) будет описываться уравнением (2).

Структура адаптивной системы управления беспилотным летательным аппаратом

Рассмотрим систему автономного адаптивного управления (рис. 4), использующую в своей структуре нечеткий блок-идентификатор (БИ), основной контур, состоящий из объекта – 83 –

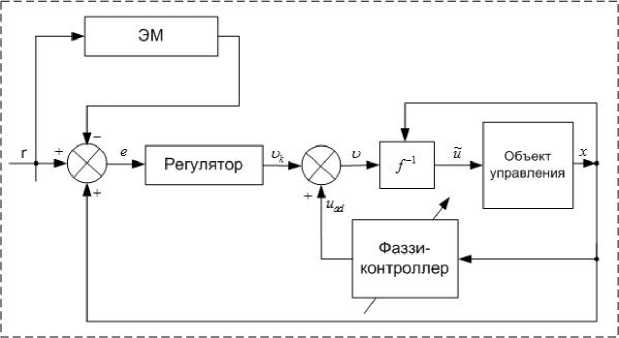
Рис. 3. Структурная схема адаптивного управления объектом

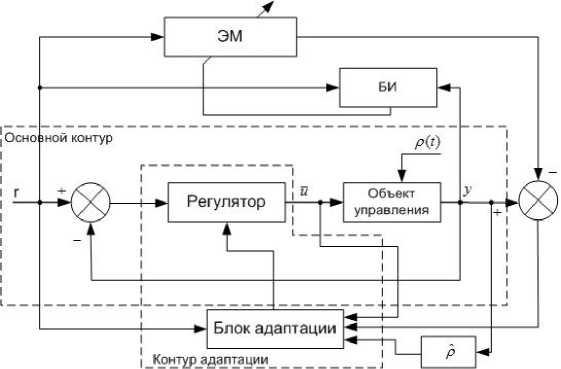
Рис. 4. Структурная схема адаптивной системы автономного управления управления (ОУ) – БПЛА и регулятора, самонастраивающуюся нечеткую эталонную модель системы (ЭМ), блок адаптации и наблюдатель р.

Полученная система выполняет следующие задачи:

• ■    обеспечение эталонных динамических характеристик системы управления БПЛА для всех режимов полета;

• ■    идентификация параметров БПЛА в полете для настройки ЭМ, при этом используется устройство с памятью;

• ■    обеспечение компенсации внешних конечномерных возмущений, для чего используется наблюдатель, формирующий оценку возмущения р ;

• ■    реализация алгоритма адаптации. Блок адаптации реагирует на ошибку e = у - у _Э между сигналами с выхода ОУ и ЭМ, а также осуществляет адаптивную подстройку к изменяющимся внешним воздействиям р ( t ).

Далее рассмотрим более подробно нечеткий блок-идентификатор (БИ).

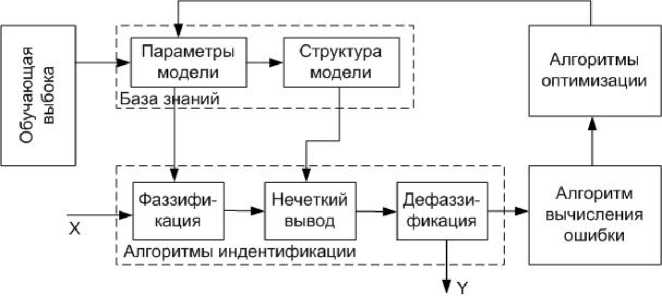
Рис. 5. Структура нечеткой модели блока идентификации

Нечеткий блок-идентификатор

Для идентификации параметров ЛА предполагается использовать адаптивную модель с нечетким выводом, со структурой, приведенной на рис. 5.

Данный блок-идентификатор позволяет устранить следующие недостатки, присущие нечетким системам:

• -    позволяет дополнять исходный набор правил, описывающий состояния системы управления, который формируется человеком и вследствие чего может иметь неполный набор правил, противоречивые или идентичные правила;

• -    позволяет оптимизировать параметры модели управления, которые изначально задаются экспертом субъективно, что снижает качество идентификации. Целенаправленное изменение параметров нечеткой модели, таких как количество, форма, относительное размещение соответствующих функций принадлежности вдоль базовых осей, оказывает существенное влияние на характер идентификации.

Блок-идентификатор состоит из базы знаний, которая представляет собой совокупность информации о базе нечетких правил и о множестве лингвистических переменных с соответствующими функциями принадлежности.

Работа по формированию базы знаний происходит в два этапа:

• -    на первом этапе база знаний формируется на основе обучающей выборки, которая состоит из параметров наблюдений с соответствующими принадлежностями к классам наблюдений и доступной априорной информации об объекте у эксперта;

• -    на втором этапе происходит параметрическая оптимизация к дискретному изменению динамики объекта управления.

Далее блок-идентификатор формирует оптимальную аппроксимацию для входных обучающих данных X(9 , M , 5 ) , где 9, M , 5 - угол тангажа, число Маха и угол отклонения руля высоты соответственно.

После обучения блок-идентификатор реализует следующее уравнение [5]:

П у ( k ) = F ( M ( k ), C [ 9 ( k ), M ( k ), 5 ( к )]),

где n y – нормальная перегрузка, C – аэродинамический коэффициент подъемной силы.

Далее будет рассмотрено моделирование блока-идентификатора системы управления БПЛА в ПП Simulink и Fuzzy Logic Toolbox [6-9].

Исследование работы нечеткого блока-идентификатора

Блок-идентификатор (БИ) спроектирован на основе систем нечеткого вывода в Fuzzy Logic Toolbox [9].

В качестве входных параметров системы нечеткого вывода будем рассматривать следующие нечеткие переменные: угол тангажа 9, число Маха M, отклонение руля высоты 5, а в качестве выходного параметра – оценку перегрузки ДПЛА nˆy. БИ моделирует зависимость (рис. 6) y в соответствии с системой нечеткого вывода типа Момдани:

n ˆ y ( k )= K z M ²( k )sgn( ϑ )[ a ˆ n ϑ ( k )³+ b n ϑ ( k )²+

+ c . (2 - M ( к )/3) У ( к )] + d n ». k ),                              (7)

где ^{y (} к),M ⁽ к), ^{5 (} к) и n y ( к ) - значения входных и выходных переменных объекта управления в дискретные моменты времени к > 0, a n , b n , c_n , d_n - аэродинамические коэффициенты ДПЛА.

Область изменения входных параметров следующая: У е [-20;20], M е [0; 0 .2], 5 е [-15;15].

Адекватность полученной нечеткой модели проверяли по следующему критерию: найти такой вектор ⁽ P , W ), чтобы [6]

RMSE = ¹ ∑ ( y r - F ( P , W , X r ))² → min,                 (8)

N r =1, N где P – вектор параметров функций принадлежности термов входных и выходной переменных; W е [0;1] — вектор весовых коэффициентов правил базы знаний; N- пары из обучающей выборки; Xr— входные переменные; yr— выход системы; F(P, W, X) — результат вывода по нечеткой базе знаний Мамдани с параметрами (P, W) при значении входов Xr.

Входы и выход нечеткой модели будем рассматривать как лингвистические переменные. Значение для переменной «угол тангажа» определяется из следующего терм-множества: ^{{PH,PM,PD,C,ND,NM,BH}} или {положительно высокий, положительно средний, положительно низкий, не меняется, отрицательно низкий, отрицательно средний, отрицательно высокий} для ϑ . Термы представим нечеткими множествами с гауссовыми функциями принадлежности. Возможный вид функции принадлежности для входной лингвистической переменной «угол тангажа» приведен на рис. 7.

Далее создадим лингвистическое описание параметров нечеткой модели БИ с помощью базы нечетких правил типа

M_i : ЕСЛИ X₁ есть А_{i 1} И ... И X_m есть A_im,

ТО Y₁ есть D_i1 И ... И   Y_n есть D_in .

Для составления и отладки базы нечетких правил использовали обучающие данные перегрузки n y (рис. 8).

После обучения нечеткой базы знаний была получена зависимость идентифицируемой перегрузки /7 y от входных переменных 9 , M , 5 (рис. 9).

Оценка перегрузки ДПЛА

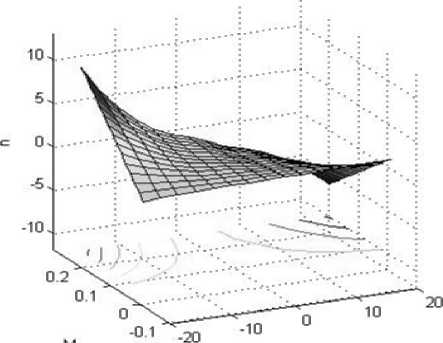
Рис. 6. Искомая зависимость: оценка перегрузки n_y ДПЛА

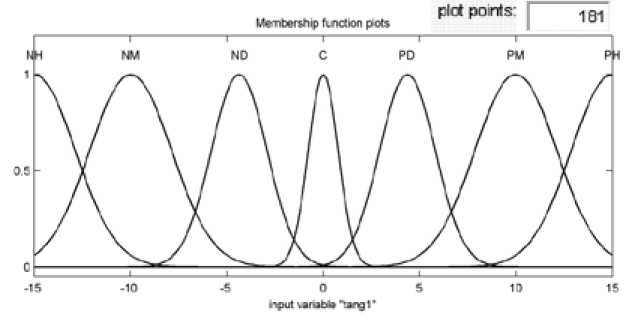
Рис. 7. Функции принадлежности переменной ϑ в Membership Function Editor

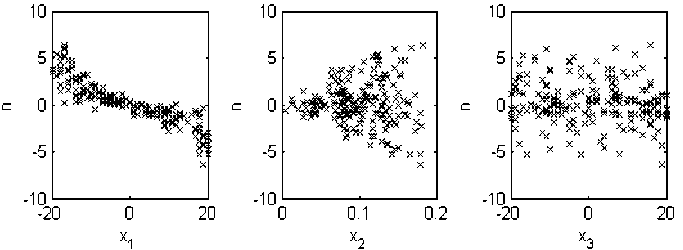
Рис. 8. Обучающая выборка для идентификации зависимости оценки перегрузки n y от угла тангажа ϑ = x 1 , числа Маха M = x 2 , отклонения руля высоты δ = x 3

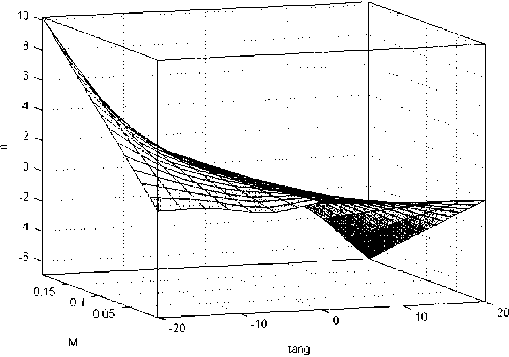
Рис. 9. Идентифицируемая перегрузка /i y , tang - тангаж

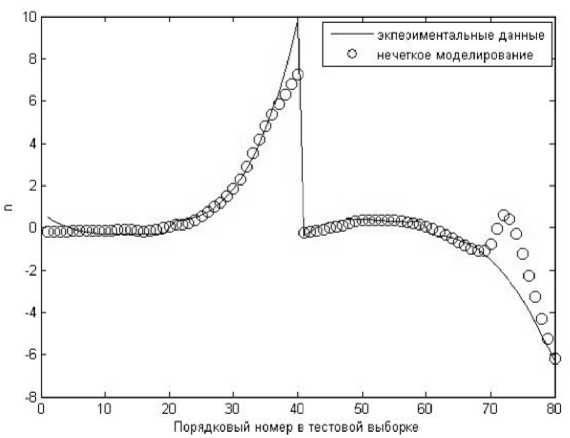
Рис. 10. Тестирование нечеткой модели БИ

Наглядное сравнение динамики экспериментальных данных из тестовой выборки с результатами нечеткого моделирования показано на рис. 10.

На рис. 10 видно, что нечеткая модель описывает динамику экспериментальных данных, однако в отдельных случаях имеются значительные расхождения в оценке перегрузки n y . Повысим точность нечеткой модели в оценке перегрузки n y с помощью обучения нечеткой базы знаний.

Обучение нечеткой модели осуществим квазиньютоновским методом [6] Бройдена-Флетчера-Голфарбда-Шэнно на протяжении 300 итераций.

Определим, как влияет длительность обучения на адекватность нечеткой модели. Для этого построим следующую зависимость (рис. 11, 12).

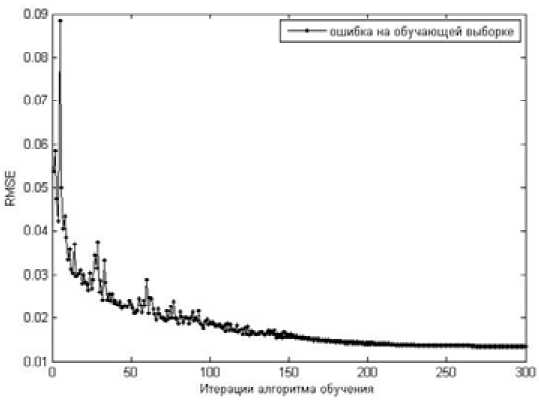
Рис. 11. Зависимость ошибок нечеткого моделирования от количества итераций обучения на обучающей выборке

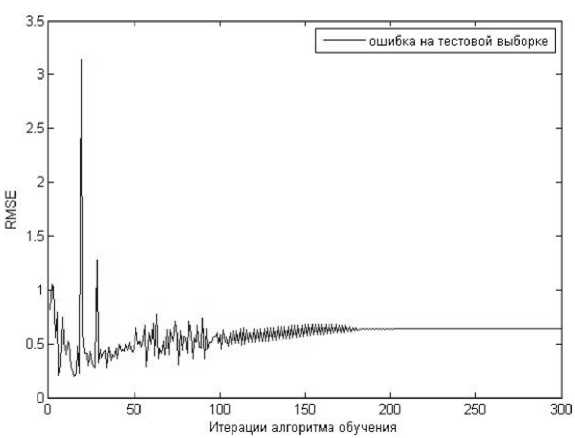
Рис. 12. Зависимость ошибок нечеткого моделирования от количества итераций обучения на тестовой выборке

На рис. 11, 12 видно, что значение невязки (8) с ростом количества итераций уменьшается. После 200 итераций квадратичная ошибка моделирования на обучающей и 50 итераций на тестовой выборках равны, соответственно, 0,0011 и 0,2361. После этого ошибка на тестовой выборке немного возрастает, и начиная примерно с выборки 49 проявляется эффект переобучения. Это объясняется тем, что вне точек обучения адекватность переобученной модели низкая – результаты моделирования очень отличаются от экспериментальных данных, поэтому рекомендуется прекращать обучение при возрастании ошибки на тестовой выборке.

После обучения и настройки нечеткой базы знаний адекватность модели заметно улучшилась, на что указывает график на рис.13.

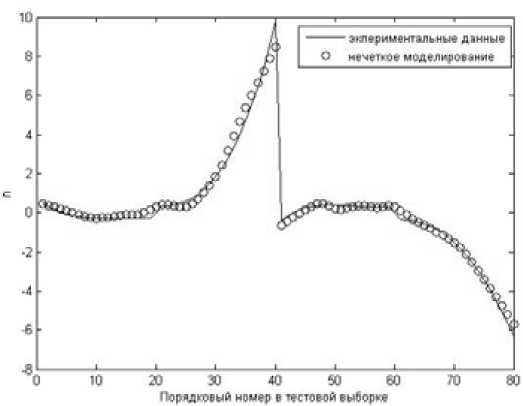
Рис.13. Тестирование нечеткой модели БИ после настройки

Заключение

Для компенсации ошибок обратного преобразования при применении ЛОС в систему вводится адаптивный элемент, в качестве которого может быть использована система нечеткого логического вывода. В реальных условиях для устранения неопределенностей может быть успешно использован фаззиконтроллер в системах управления с обратной связью.

В результате исследования была показана целесообразность применения адаптивной эталонной модели с блоком-идентификатором на нечеткой логике, которая обеспечивает адаптацию эталонной модели к широким изменениям режимов полета ДПЛА.

Работа публикуется при поддержке Программы развития Сибирского федерального университета.