Нечётко-множественная кластеризация поступлений в московский бюджет от рынка наружной рекламы

Автор: Лабунец Леонид Витальевич, Лебедева Наталья Леонидовна, Чижов Михаил Юрьевич

Журнал: Вестник Российского нового университета. Серия: Сложные системы: модели, анализ и управление @vestnik-rosnou-complex-systems-models-analysis-management

Рубрика: Математическое моделирование в экономике и управлении

Статья в выпуске: 4, 2014 года.

Бесплатный доступ

В статье на основе методов интеллектуального анализа данных продемонстрирована взаимосвязь вероятностных и нечётко-множественных подходов к анализу и моделированию поступлений в московский бюджет от объектов наружной рекламы (ОНР). Представлена методика лингвистического анализа распределения поступлений в бюджет в виде аппроксимации гистограммы, сглаженной сдвигом полигауссовой модели. Рассмотрены основные этапы нечёткого логического вывода и кластеризации ОНР по критерию поступлений с помощью байесовского классификатора и метода главных компонент

Преобразования бокса - кокса, диаграмма рассеяния, квазистатистики, экспоненциально взвешенные оценки мешалкина, лингвистический анализ гистограммы, em-алгоритм, байесовские оценки, нечёткий логический вывод, метод главных компонент

Короткий адрес: https://sciup.org/148160191

IDR: 148160191

Текст научной статьи Нечётко-множественная кластеризация поступлений в московский бюджет от рынка наружной рекламы

Описательные и прогнозные модели, основанные на применении современных методов и алгоритмов Data Mining. позволяют выявить закономерности, содержащие знания, необходимые для оценки финансовых рисков и прогнозирования рыночных тенденций. В докладе проанализирована проблема формирования описательных моделей эффективности объектов наружной рекламы (ОНР). Надежной методической основой такого рода моделей являются

ВЕСТНИК 2014. ВЫПУСК 4

алгоритмы нечеткой кластеризации различных типов ОНР по уровню поступлений в бюджет. Представлен экспертный подход к анализу исходной информации, который позволяет учесть ее неопределенность. Плодотворным в этом смысле является применение систем обработки знаний экспертов с помощью алгоритмов нечеткого логического вывода [1; 2].

Модель многомерных данных

Трехмерная модель исходных данных представляет собой информационный «куб» [3] со следующими измерениями:

1. «время» в виде последовательности месяцев n = 1,2,..., N ( N = 48 ) в период с 2008 по 2011 год включительно;
2. «округ» в виде упорядоченной последовательности административных округов г. Москвы m = 1,2,..., M ( M = 11 ) , представленных в таблице 1 по состоянию на 2011 год;
3. «тип ОНР» в виде упорядоченной последовательности типов наружной рекламы k = 1,2,..., K ( K = 30 ) , представленных в таблице 2;

Таблица 1

Административные округа

m	Наименование
1.	Общегородской заказ (ОГЗ)
2.	Восточный административный округ (ВАО)
3.	Западный административный округ (ЗАО)
4.	Зеленоградский административный округ (ЗелАО)
5.	Северный административный округ (САО)
6.	Северо-восточный административный округ (СВАО)
7.	Северо-западный административный округ (СЗАО)
8.	Центральный административный округ (ЦАО)
9.	Южный административный округ (ЮАО)
10.	Юго-восточный административный округ (ЮВАО)
11.	Юго-западный административный округ (ЮЗАО)

Кластерная структура данных исследовалась в пространстве Евклида одиннадцати административных округов г. Москвы. Исходными при- знаками в этом случае являются компоненты вектора столбца

x = ( x j

^x m ) )

в виде поступлений в московский бюджет от ОНР, консолидированных по месяцам в периоды 2008 ( 1 < n < 12 ) , 2009 ( 13 < n < 24 ) , 2010 ( 25 < n < 36 ) и 2011 ( 37 < n < 48 ) годов. Здесь и далее зависимость векторов от индекса времени n опускаем для упрощения записи.

Типы наружной рекламы

Таблица 2

23.	Транспарант-перетяжка
24.	Тумба отдельно стоящая
25.	Щит на временном ограждении
26.	Щит на ограждении
27.	Щит отдельно стоящий
28.	Электронный экран на здании
29.	Электронный экран на крыше
30.	Электронный экран отдельно стоящий

Иными словами, для каждого года выборка обучающих примеров представляет собой блочную матрицу X = ( X 1 :•••: X K ) размером M х K .

- т

Текущий столбец X k = ( X 1 k ,..., X_Mk ) матрицы – это поступления в бюджет от k -го типа рекламы в административные округа за фиксированный год.

Разведочный анализ данных выполнялся после предварительного преобразования Бокса – Кокса (БКП) [4] обучающей выборки для каждого административного округа. Величина смещения БКП е выбиралась из условий X mk + е > 0, m = 1,2,...,M, к = 1,2,^,K . Оптимальное значение параметра gm БКП удовлетворяли критерию максимума логарифма правдоподобия L(gm). Зависимости логарифма правдоподобия L ( gm) от параметра gm для поступлений в московский бюджет от ОНР за 2008 г. в один- надцати административных округах и значения смещения е = 10-8 иллюстрирует рис. 1.

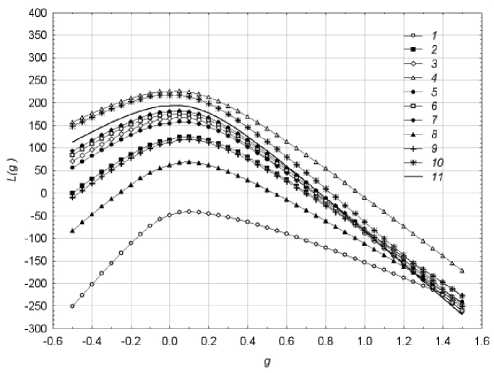
Рис. 1. Зависимость логарифма правдоподобия от параметра преобразования Бокса – Кокса

Результаты расчета показали, что оптимальные оценки параметра БКП лежат в интервале - 0,15 < g_m < 0,1, m = 1,2,..., M . Графики БКП для указанных выше значений параметра g_m демонстрирует рис. 2.

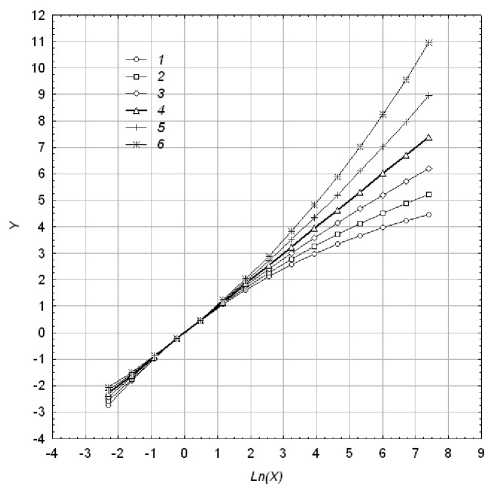
Рис. 2. БКП для различных значений параметра g :

1 - g = - 0,15; 2 - g = - 0,1; 3 - g = - 0,05;

4 - g = 0; 5 - g = 0,05; 6 - g = 0,1

Удобным инструментом разведочного анализа данных является диаграмма рассеяния (ДР), содержащая K точек в M-мерном пространстве . T преобразованных признаков Yk = ( Y1 k, ^, YMk) , к = 1,2,^,K. Здесь и в дальнейшем зависимость от параметра gm БКП опускается. Топологию ДР удобно исследовать методом ‟Grand Turˮ динамической визуализации многомерных данных [5]. Ортогональная проекция ДР на одну из гиперплоскостей в пространстве одиннадцати административных округов г. Москвы для поступлений в 2008 г. представлена на рис. 3.

ВЕСТНИК 2014. ВЫПУСК 4

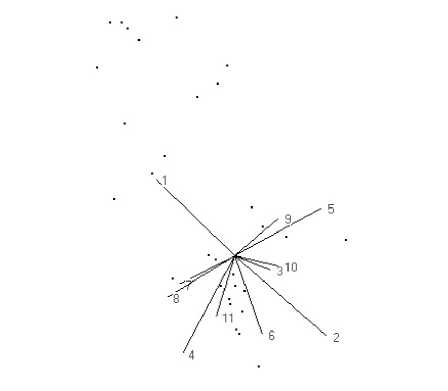
Рис. 3. Ортогональная проекция многомерной ДР на плоскость визуализации

ВЕСТНИК 2014. ВЫПУСК 4

Анализ формы ДР с различных ракурсов свидетельствует о наличии достаточно выраженных генеральных направлений в пространстве преобразованных признаков. Иными словами, имеет место значимая корреляция признаков y = ( У 1 , — , У м ) .

Нечетко-множественый и вероятностный подходы к анализу данных

Существенной проблемой формирования адекватных описательных статистик является наличие жесткого ограничения малого объема данных. В нашем случае гипотетический объем выборки K = 30 ассоциирован с количеством типов ОНР Однако значения X_mk = 0, свидетельствующие об отсутствии поступлений в округа от некоторых типов рекламы, приводят к необходимости игнорировать аномально низкие величины признаков. Это снижает фактический объем данных. Известно, что в соответствии с правилом Старгеса (Sturges’s rule) [6] объем выборки, необходимый для формирования гистограммы нормального распределения, содержащей как минимум 5 разрядных интервалов, рассчитывают по формуле K min = 2 ⁵ ^- ¹ = 2 4 = 16 .

Рациональное решение проблемы малого объема выборки основано на нечеткомножественном подходе к анализу данных. В рамках такого подхода конструктивным является понятие квазистатистики, введенное в работе [2, с. 28]. В частности, консолидированные по годам выборки поступлений в бюджет от 30 типов ОНР в каждый из одиннадцати округов г. Москвы будем считать достаточными, чтобы с приемлемой степенью достоверности сформировать оценки законов распределения наблюдений.

С другой стороны, нет оснований кардинально разграничивать нечетко-множественный и вероятностный подходы к интеллектуальному анализу данных. В указанном смысле следует отметить результаты теоретического анализа, представленного в разделе 1.4.6 работы [7], интерпретирующего нечеткие множества как «проекции» случайных множеств. Последующее содержание статьи демонстрирует плодотворное сочетание нечетко-множественной и вероятностной методологий.

Исключение аномальных значений из данных

Аномальные значения в данных существенно искажают результаты стандартного оценивания основных статистик. Одним из рациональных методов исключения влияния загрязнений выборки являются экспоненциально взвешенные оценки (ЭВО) характеристик положения и масштаба Л. Д. Мешалкина. Одномерные робастные ЭВО математического ожидания (МО) am (2) и среднего квадрата отклонения (СКО) sm (2), m = 1,2,—, M представляют собой решение соответствующей системы нелинейных уравнений [8].

Структура ЭВО обеспечивает автоматическое подавление выбросов в данных, если параметр эффективности статистик 2 > 0 . Аномально большие значения Y_mk формируют большие расстояния Махаланобиса, поэтому взвешиваются экспоненциальными весами, достаточно малыми, чтобы не вносить значимого вклада в результирующую оценку. В работах А.М. Шурыгина [8] показано, что ЭВО являются оценками минимума контраста. Однако снижение эффективности ЭВО повышает их устойчивость к нарушению гипотезы нормальности плотности распределения вероятности (ПРВ).

Процесс сходимости алгоритма расчета ЭВО с параметром 2 = 1 для характеристик положения и масштаба поступлений от ОНР за 2008 г. в случае общегородского заказа ( m = 1) иллюстрирует рис. 4

ЭВО удобны для формирования границ, отделяющих кластер «типичных» значений Y_mk , k = 1,2, — , K от выбросов. Результаты моделирования показали, что в качестве границ рационально выбирать правило «двух сигм», т.е. величины ( a m ± 2 s_m ) . В соответствии с указанным правилом выполнялось масштабирование данных:

(у _у( mⁱⁿ⁾l / 1 у( max)_у( min)!

^y mk mk m \ \ m m J,
k = 1,2,..., K m ,

очищенных от загрязнений, с целью преобразования их к стандартному интервалу от 0 до 1. Здесь Y m min ) и Y m ^max ⁾ - робастные оценки точной нижней и верхней границ кластера «типичных» значений; K_m – количество наблюдений в кластере.

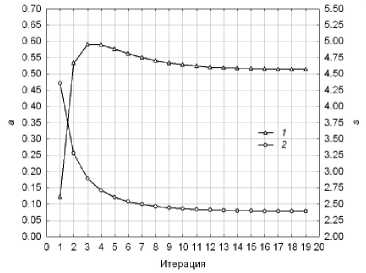
Рис. 4. ЭВО характеристик положения и масштаба: 1 – МО; 2 – СКО

Гистограмма, сглаженная сдвигом

В рамках понятия квазистатистики адекватной моделью закона распределения для выборки данных, очищенных от загрязнений, является ASH-оценка. Процедуру сглаживания классической гистограммы окном данных Wm ( n ) описывает уравнение дискретной свертки [6]. Ширина разрядных интервалов выбиралась в соответствии с робастной оценкой Фридмана – Дьякониса 2 IQm J ^ К m , где IQm - интерквартильный диапазон нормированных поступлений в бюджет в m-ом административном округе за фиксированный год. Кроме того, ширину разрядных интервалов классической гистограммы выбирали так, чтобы их количество было не ме- нее пяти.

Окно данных W m ( n ) выбирали из условия Е п-1- i W m ( n ) = i m . В этом случае ASH-оценка распред ^m еления интегрируема с единицей. Такой нормировке удовлетворяет обобщенное окно вида: / im - 1

Wm ( П ) = imKer ( njim )/ Е Ker ( llim ) , l=1-im где Ker (u) - положительная четная функция ядра, заданная на стандартном интервале [–1; 1] и интегрируемая с единицей. Популярные модели ядерных функций приведены в [6, с. 140]. На рис. 5 представлена ASH-оценка распределения нормированных поступлений в бюджет за 2008 г. для общегородского заказа.

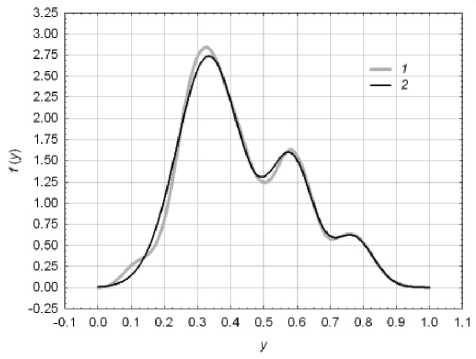
Рис. 5. Оценки распределения нормированных поступлений в бюджет:

1 – ASH; 2 – полигауссовская аппроксимация

Конечная смесь стандартных распределений

Теоретически обоснованной методической основой процедуры лингвистического анализа гистограммы [9] является модель конечной смеси стандартных распределений:

Nm f m (у I ^ m ) = ^ Pmn Ф mn (у I

N m П = 1

У p =1 mn , n =1

c mn ’ s mn ) ^,

где P_mn , n = 1,2,..., N_m и N_m - априорные веса лингвистических классов уровней «доходности» ОНР и их количество для m -го административного округа; Ф mn ⁽ y\c mn , s mn ) - парциальные распределения с характеристиками положения c_mn и масштаба s_mn лингвистических классов. В дальнейшем там, где это не вызвано необходимостью, зависимость параметров модели (3) от номера m административного округа опускаем для сокращения записи.

В рамках представления (3) байесовский подход к формированию параметрической мо- дели лингвистической переменной сводился к описанию функций принадлежности классов апостериорными весами:

wn (у| 9 )= Pn Ф n ( y |cn , sn )/ f ( y| 9), n = 1,2,^, N (4)

Оптимальную оценку вектора параметров 6 = ⁽ P 1 ,^, PN , c 1 ,^, cN , s 1 , ^ , S N ) модели (3) получают с помощью эффективного в вычислительном отношении EM -алгоритма. Стандартным критерием оптимальности параметров модели является функционал правдоподобия Фишера:

6 opt = argmax { L ( 6^)}

1θ

L ( 9 ) = J ^ln ^{ / ( ^ | 9^)} f ( y ) dy .

Рациональным критерием оптимальности является также функционал расстояния Бхатача-рия [10]:

9 1 opt = arg min ^{ D ⁽9^)} ^,

ВЕСТНИК 2014. ВЫПУСК 4

l 0 J

Решением указанных выше задач условной оптимизации является система нелинейных уравнений, представленная в [10]. Итерационная процедура решения такой системы уравнений [11, с. 1299] позволила аппроксимировать ASH- оценку распределения нормированных поступлений в бюджет за фиксированный год в текущем административном округе параметрической моделью (3).

Выбор количества классов N терм множества лингвистической переменной уровней «доходности» ОНР и начальных оценок параметров модели (3) в значительной степени является субъективным и основан на мнении эксперта.

Популярной на практике является полигаус-совская модель конечной смеси распределений (3), в которой в качестве парциальных применяют нормальные распределения:

n ( y\cn , sn ) rz—exp{ (y cn ) 122 sn )} sn 2π

Полигауссовская аппроксимация ASH-оцен- ки распределения нормированных поступлений в бюджет за 2008 г. для общегородского заказа представлена на рис. 5. Явно выраженная мо-

ВЕСТНИК 2014. ВЫПУСК 4

дальная структура распределения свидетельствует о наличии трех классов уровней «доходности» ОНР – низкой, средней и высокой. Байесовскую модель (4) соответствующей трехуровневой лингвистической переменной демонстрирует рис. 6.

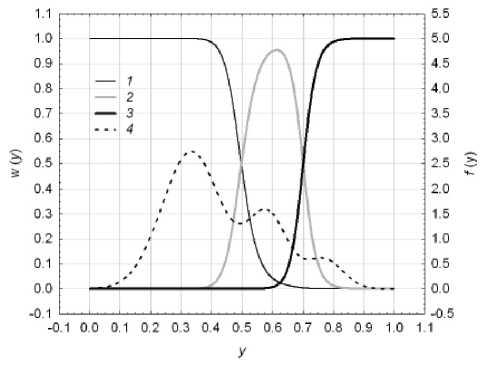
Рис. 6. Байесовская модель лингвистической переменной: 1, 2, 3 – функции принадлежности классов низкой, средней, высокой «доходности» ОНР;

4 – полигауссовская аппроксимация ASH-оценки распределения

Процесс сходимости EM -алгоритма обучения модели (3) по критерию правдоподобия иллюстрирует рис. 7. Из графиков видно, что сходимость параметров модели к оптимальным значениям достигается практически за 10 итераций как по критерию правдоподобия Фишера L ( i ) , так и по критерию расстояния Бхатачария D ( i ) .

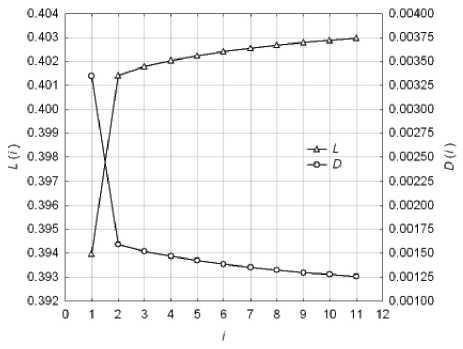
Рис. 7. Сходимость EM -алгоритма по итерациям i обучения модели

Нечеткий логический вывод

Ранжирование ОНР по уровню поступлений в бюджет выполнялось с помощью алгоритмов нечеткого логического вывода. Одним из основных этапов формирования моделей приближенных рассуждений является агрегирование нечеткой информации об объекте анализа. В нашем случае – это композиция средних уровней «доходности» лингвистических классов. Иными словами, комплексный показатель эффективности различных типов ОНР представлен в виде байесовской модели учета неопределенности:

N m

У(AC>=Y c w ymk mn mn n =1

m = 1,2, . , M ,

k = 1,2, ^ , K ,

где c _mn и y _mk – средняя «доходность» (узловая точка [2, с. 157; 9]) n -го лингвистического класса и нормированные поступления в городской бюджет от k -го типа ОНР в m -ом административном округе за фиксированный год.

Последовательность значений y mAC ) k = 1,2, ..., K упорядоченная по убыванию, ранжирует различные типы ОНР по их «доходности» в m -ом административном округе за фиксированный год. Кроме того, байесовский классификатор, зачисляющий k -й тип ОНР в n -й класс «доходности» по правилу победителя, т.е.

( ^ ^"

V , \ 0 > W V , У , ymk m m j ymk m , j = 1,2,...,Nm , j ^ n реализует лингвистическую кластеризацию ОНР. В качестве примера в таблицах 4–6 представлены результаты такого рода кластеризации по уровням поступлений в бюджет за 2008 г. для общегородского заказа.

Таблица 4

:S О

о в

о V 3 аа v

ОО ОО

сч ОО

мч

СП

ОО

<п сд

о о мп

ОО 40

о о о о о о

40 04 04 04 04

о сч

04 04

04 о

сч сп

хг

04 о

00 04 04 «Г,

ХГ

ГО 1Л 04 40

40 m 04 1-4 40 К)

о о о о о о

сч

о о

ОО сч о

о о

04 40

vn сд о

04 04

сч

ОО сч

04 40 ОО сч о

СП

о о о о о о

о о о

сч о

о о о

04 04 О О О О

о 40

О О

мп

о о

04 ОО сч о о

МП

сч

04 МП о

сч о о о о о о о

о о

40 04

04 ОО

О 04

оо

vn МП 04

сч

04 ОО

о 04

сч S о

сч

ОО

г-

хГ

г-

В О У

ж Д 2

н о

о и й

(D ^ н о

cd у

(D Д

н Д

Он

И cd э

Й д

сч

(D (D ч о хо

2 й ^ cd

о и и cd д

(D о и и (D н о cd к

cd д и о и cd н

д 2

(D Он о к о

>д о Й о н

(D Й о

cd и

и ж

(D н 2 и

о н о

о и й

и се & m

)В

И И о &

(D Д

хо

зД О н о о

Й У

(D (D

Ч О хо

о н о

3S о и « о

2 й « cd

cd « со cd И

Ж (D Н 3

о н о

о и й

cd хо

cd н СХи О к о И cd

X cd

Й о и cd Н О о

cd И

(D сц

:В

О у

аа

:В В

В о»

Ч В

в аа

S В в

Я о

мп мп 40 ОО

40 40

40 СЧ 40

мп о

О 40 СЧ мп

ОО 40 СЧ сч мп

мп

о мп

О 40 сч 40

мп

ОО о

о о

40 ОО

О О о

сч 40

О О О

о о о о

40 О О О О

00 ID ХГ m ГП

40 ХГ ID ГП 1Г> 04 О

^ сч сч о

04 1Л

04 ХГ СП 1-Н

40 О

т W СП 1-4 ID 40

О О

мп мп

04 мп 04 СЧ сч о

04 О S О

ОО

мп ОО

СП

40 ОО

мп

о 40

мп

мп о

сч

мп о

мп

ОО

мп

ОО

04 мп

мп

СЧ сч

СП

’—¹

мп

04 СЧ

в в S

В О S

2 й н о cd У

Ж (D ^ СО (D О & ^ cd И cd ^ Й о и cd Н о^

& И о S

cd Н

2 cd й

ч о хо

о о к

S д cd со Д Д cd о

Д t^ д н

rt о

& д

Д о Д К Д

В я Н * 5 s § в о ч -& U

S в

X се

В В н о ч о в

X в и

ЕВ

X се

се Ч ■&

се В

се

(D сц

Й X

сч

(D (D д (D 2

2 й « cd 2 о g

о д д cd Д

(D О д д (D н О cd К

2Д о н о о

Й д

(D (D д (D

2 д о

о н о

)Д о д « о

2 й « cd

2 о g

се П го

се В

§ 1Г>

В о 2 я

« S

(D 3

& се В В се & m

5В В В В о

ВЕСТНИК 2014. ВЫПУСК 4

гц

D ОО

гц Os ОО

ОО tn

о о 40 Os

ОО

о tn

ОО

ГЦ 40 40

IT)

о о

о о о о о о

О О О О О О

О О о о о о

О о о о о о

О О о о о о

о о о о о о

О О о о о о

о о о о о о

Os Os

о ГЦ

tn о

ОО ОО

о о

ОО 40

о ГЦ о

о о

40 ГЦ

о о

ОО Os о о о

ОО Os tn о о о

о о о о о о

ГЦ о о 40 Os

W гц о гц ^г OS о

ГЦ iH id ^г ID OS о

ГЦ m ID Os

OS о

m SO ID OS 00 OS о

ГЦ Os OS

40 W о 40 Os OS о

ГП W о OS OS OS

ГЦ о ^ Os OS OS о

о о о о о о

й Os tn

Os о

ОО 40

9 о

гц

tn 40

ОО

ОО ГЦ

о о Os

ОО

ГЦ ОО о ГЦ

о Os

ГЦ

ОО

ГЦ

Os tn

40 о о о о о о о

40 о Os Os

40 tn

40 tn tn со

tn о

гц

tn гц

ГЦ

ОО

ГЦ

40 ГЦ

’—¹

ГЦ

ОО

Я Я я

о. н

я о я

я я н

о о и X

5 X

& rt

S X се се

■е се И се 1

(D Он

t* О н о о и й 5

rt И

н ^3 i

и о

к cd И о о И

cd к

О о

cd й

И И (D И

о о

и 5 (D Й ю О

S S

5 о И

и се И

cd со S

(D Он о к о

ж о и о н (D О

(D И

cd И

Ж (D н 3 и о

t^ о н о

о и й

(D Й

Ю О

И И (D Й И О И cd

Н О о &

(D Й ю О

2 л rt се

о ч

м S

се S

о ч

о S

X S и

& rt

X се

се

-^^

S ^м'

се

S ^

§ 8

(D О Сц ю

S S

S се П м

се S

S се & m

S S о

S S и

о В

S S о ■&

ч о н

В &

S 5S

S § (D 3 и

о о

3 и (D Й

Ю О (D 3 Й о к

S и (D и (D S

S S S о П Й се

о се S Ё

й cd ^ S m

2 л rt се

о ч

В м

s'¹

се П м

се S

X се

ч о

S и

& rt

X се

се

-^^

Я §

5 ^ cd

Рч В

cd в се Ч И

К се В S Q

О К

н (D о

Эй о и Й 5

О Он и о cd

И cd 1

Он

Заключение

В работе проанализирована тесная взаимосвязь вероятностного и нечетко-множественного подходов к анализу и моделированию эффективности различных типов ОНР по критерию поступлений в московский бюджет. Представлена методика учета фактора неопределенности, обусловленного малым объемом выборки на основе применения фундаментальной процедуры сглаживания экспериментальных данных. В частности, проиллюстрирована эффективность лингвистического анализа распределений исходных признаков в результате комбинации непараметрической модели в виде гистограммы, сглаженной сдвигом, и параметрического описания в виде конечной смеси стандартных плотностей.

Список литературы Нечётко-множественная кластеризация поступлений в московский бюджет от рынка наружной рекламы

Ведерников В.В. Нечётко-множественное моделирование в анализе и прогнозировании экономических явлений и процессов: исторический аспект //Проблемы современной экономики. -2006. -№ 1 (17). -URL: www.m-economy.ru.
Недосекин А.О. Нечётко-множественный анализ рисков фондовых инвестиций. -СПб.: Сезам, 2002. -181 с.
Барсегян А.А. Технологии анализа данных: Data Mining, Visual Mining, Text Mining, OLAP/А.А. Барсегян, М.С. Куприянов, В.В. Степаненко, И.И. Холод. -2-е изд., перераб. и доп. -СПб.: БХВ -Петербург, 2007. -384 с.
Box, G.E.P., Cox, D. R. An analysis of transformation//Journal of the Royal Statistical Society. Series B (Methodological). -1964. -Vol. 26. -№ 2. -Pp. 211-252.
Buja, A., Cook, D., Asimov, D., Hurley, C. Theory and computational methods for dynamic projections in high-dimensional data visualizations//Journal of Computational and Graphical Statistics. -1999. -Vol. 8. -№ 3. -Pp. 1 -24.
Scott D.W. Multivariate Density Estimation: Theory, Practice, and Visualization. -N.Y.: John Wiley & Sons, Inc, 1992. -317 c.
Орлов А.И. Прикладная статистика. -М.: Экзамен, 2006. -671 с.
Шурыгин А.М. Прикладная стохастика: робастность, оценивание, прогноз. -М.: Финансы и статистика, 2000. -224 с.
Недосекин А.О., Фролова С.Н. Лингвистический анализ гистограмм экономических факторов//Вестник ВГУ. -Серия: «Экономика и управление». -2008. -Выпуск 2. -С. 48-55.
Лабунец Л.В. Рандомизация многомерных распределений в метрике Махаланобиса//Радиотехника и электроника. -2000. -Т. 45. -№ 10. -С. 1214-1225.
Лабунец Л.В., Лукин Д.С., Червяков А.А. Реконструкция отражательных характеристик 3D-объектов в однопозиционной системе оптической локации//Радиотехника и электроника. -2012. -Т. 57. -№ 12. -С. 1289-1300.

Еще

Статья научная