Неинвазивные методы контроля в диагностике вязкоэластических свойств кожного покрова

Основными методами, используемыми врачами в дерматологии и косметологии, являются внешний осмотр, оценка эластичности и упругости кожи путем пальпации. Однако в ряде случаев при решении задач диагностики дерматологических заболеваний традиционно применяемые, субъективные методы оценки состояния кожи являются малоинформативными. В связи с этим актуальной является проблема объективного инструментального контроля состояния кожного покрова.

В последние годы активно ведутся работы по созданию устройств, основанных на получении объективных данных о механических, оптических, акустических, электрических параметрах кожи неинвазивными методами [1, 2]. Диагностика вязкоэластических свойств кожи затруднена из-за сложности ее морфологического строения. Наиболее приемлемым, а в некоторых случаях и единственным, является неразрушающие методы контроля, которые позволяют, не нарушая структуру, проводить диагностику различных состояний кожного покрова [3]. Механические свойства компонентов дермы во многом обусловлены растяжимостью ее эластиновых и коллагеновых волокон, их количественным соотношением и пространственной ориентацией. В процессе возрастных изменений и в случаях развития патологических состояний при нарушении

Вальков Алексей Федорович, аспирант водного баланса и дезорганизации пространственной структуры соединительно-тканных волокон изменяются механические свойства, кожа теряет эластичность.

Цель данной работы: исследование возможности мониторинга состояния кожного покрова путем определения ее упруго-вязких характеристик.

Для использования этого способа и выявления диагностических признаков создана математическая модель, описывающая взаимодействие исследуемого материала с индентором, оснащенным системой датчиков, контролирующих процесс распространения малых возмущений. С точки зрения математического моделирования кожа представляет собой сложный неоднородный многослойный объект, поэтому для определения реакции кожного покрова далее рассматривается упрощенная математическая модель, которая основана на предположении о том, что кожа описывается дискретной моделью, содержащей две массы, связанные между собой упруго-вязкими элементами. Упрощенная расчетная схема представлена на рис.1. На схеме приняты следующие обозначения: m 1 – масса бойка ударника (индентора); m 2 , m 3 – приведенные массы слоев кожного покрова, участвующие во взаимодействии; с 1 , с 2 , с 3 – приведенные коэффициенты жесткостей слоев кожного покрова, участвующие во взаимодействии; b 1 , b 2 , b 3 – приведенные коэффициенты вязкого сопротивления в слоях кожного покрова; с а, b а – приведенные коэффициенты жесткости и вязкого сопротивления подвески индентора; x 1 , x 2 , x 3 – обобщенные координаты перемещения эпидермиса (x 1 ), собственно дермы (x 2 ), подкожно-жировой клетчатки (x 3 ).

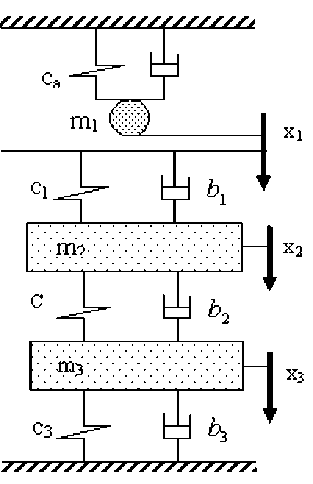
Рис. 1. Упрощенная расчетная схема

Нами была построена математическая модель взаимодействия поверхности кожи с измерительным элементом. На первом этапе выполнены теоретические исследования с применением численного интегрирования дифференциальных уравнений математической модели. Эти исследования позволили определить параметры упругой подвески индентора, обеспечивающей безотрывное движение бойка. Анализ виброграммы показывает, что развитие возмущений в коже происходит с запаздыванием, т.е. сначала индентор деформирует поверхностный слой кожи, далее возмущение распространяется в нижележащие слои. По результатам расчетов было установлено, что перемещение бойка может быть приближенно описано экспоненциальным законом:

Х(t) = А 0 ∙exp(- β t)∙cos( ω t), (1)

где β – параметр, определяющий диссипативные свойства, ω – параметр, определяющий упругие свойства кожи, А 0 – величина, определяемая начальными настройками упругой подвески индентора. Идентификация коэффициентов β и ω по экспериментально полученным данным позволяет количественно оценить упу-го-диссипативные свойства кожного покрова.

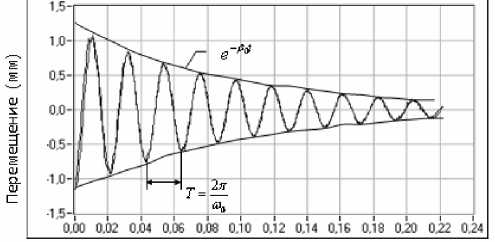
Целью дальнейших исследований являлось определение упруго-диссипативных параметров кожного покрова по результатам обработки кривой затухающих совместных колебаний индентора и кожного покрова. Предлагаемая методика основана на том, что движение индентора и исследуемого участка кожного покрова осуществляется совместно. Примеры виброграмм перемещений бойка-индентора в холостом режиме и в контакте с диагностируемым участком кожного покрова представлены соответственно на рис. 2 и рис. 3.

Время (с)

Рис. 2. Виброграмма перемещения бойка-индентора в холостом режиме

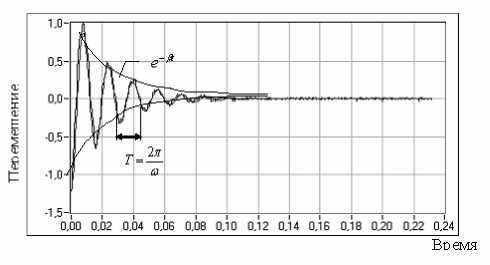
Рис. 3. Виброграмма перемещения бойка-индентора при свободных колебаниях совместно с тестируемым материалом

Определение упруго-вязких параметров кожного покрова производилось путем идентификации коэффициентов уравнения свободных затухающих колебаний по формуле (1). При идентификации неизвестных параметров затухания β и частоты ω свободных затухающих колебаний участка кожной поверхности в среде LabView использовались два метода: метод Гильберта и метод Левенберга-Макгварда. Метод нелинейной оптимизации Левенберга-Макгварда использует для поиска минимума комбинированную стратегию – линейную аппроксимацию и градиентный спуск; переключение с одного метода на другой происходит в зависимости от того, была ли успешной линейная аппроксимация. Для определения частоты использовалось быстрое преобразование Фурье, а для определения коэффициента затухания воспользуемся построением огибающей при помощи функции Гильберта и дальнейшей аппроксимацией, позволяющий рассчитывать функцию Гильберта H(t) по исходной функции x(t):

_{H ( t ) =} 1 _⋅ x ( s ) _{ds =} 1 _⋅ x ( t - s ) - x ( t + s ) _ds π t - x π s

-∞               0

При этом огибающую получаем по формуле

A (t) = 4 x 2( t) + H 2( t)       (3)

График, представленный на рис. 4, демонстрирует исходную виброграмму, функцию Гильберта и огибающую.

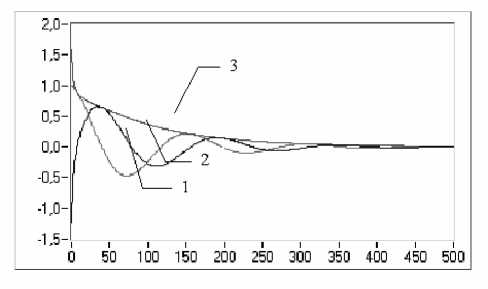
Рис. 4. Расчетные функции (1 – исходный сигнал, 2 – функция Гильберта, 3 – огибающая)

В результате идентификации упругодиссипативных параметров кожного покрова были получены безразмерные коэффициенты: в = вв0- безразмерный коэффициент затухания, оценивающий диссипативные свойства кожи и » = °®- безразмерная частота свободных колебаний, характеризующая упругость, где ω0 – частота свободных колебаний бойка-индентора на упругом подвесе в холостом режиме, β0 – коэффициент затухания в холостом режиме.

Выводы: упруго-диссипативные свой с тва кожи определяются двумя параметрами: в -безразмерным коэффициентом затухания и » – безразмерной собственной частотой. Разработанная модель позволяет проводить численные исследования поведения упругодиссипативных характеристик тестируемого материала с учетом взаимодействия экспериментальной установки и кожного покрова.

Работа выполнена в рамках ГК №14.740.11.0249 Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг.