Неэргодичность математической модели компьютерной сети случайного доступа

Рассмотрим сеть связи случайного доступа. Обращение к общему ресурсу (моноканалу) реализуется протоколом случайного множественного доступа с оповещением о конфликте. Абонентская станция, сформировав сообщение, отправляет его на общий ресурс. Если ресурс свободен, то начинает осуществляться немедленная передача сообщения, которая заканчивается успешно, если за это время другие заявки не поступали. Если же за время передачи одного сообщения поступает другое, то происходит наложение сигналов, в результате чего сообщения искажаются. Сообщения, попавшие в конфликт, а также поступившие на этапе оповещения о конфликте, считаются искаженными и переходят в источник повторных вы- зовов (ИПВ), откуда вновь подаются на обслуживание после случайной задержки.

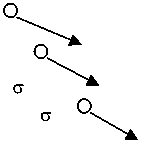
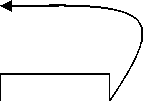
В качестве математической модели сети случайного доступа рассмотрим (см. рисунок) однолинейную немарковскую RQ-систему (Retrial Queues) с конфликтами заявок, на вход которой поступает простейший поток заявок с интенсивностью λ. Требование, обратившееся к прибору и заставшее его свободным, немедленно занимает прибор и начинает обслуживаться в течение случайного времени, имеющего произвольную функцию распределения B(x). Если за время обслуживания заявки другие требования не поступали, то обслуживаемая заявка покидает систему после полного завершения обслуживания. Если прибор занят, то поступившая и обслуживаемая заявки вступают в конфликт и обе переходят в ИПВ, где осуществляют случайную задержку, продолжительность которой имеет экспоненциальное распределение с параметром а, а на приборе начинается этап оповещения о конфликте, продолжительность которого имеет функцию распределения A(x). Из ИПВ после случайной задержки заявка вновь обращается к прибору с повторной попыткой его захвата. И если прибор свободен, то заявка из ИПВ немедленно занимает его для обслуживания. Если же прибор занят, то вновь возникает конфликт и обе заявки переходят в ИПВ.

Таким образом, математической моделью сети случайного доступа будем называть RQ-систему с конфликтами заявок и оповещением о конфликте.

Важным вопросом в теории массового обслуживания является определение условий существования стационарного режима в RQ-системах. Несмотря на обилие работ [1; 2], посвященных данному вопросу, проблема эргодичности RQ-систем с конфликтами заявок не нашла должного отражения в научной литературе. В работе мы использовали условие Каплана и теорему Сеннота [3] для доказательства неэргодич-ности математических моделей компьютерных сетей связи с конфликтами заявок.

Неэргодичность математической модели определяет неустойчивость функционирования рассматриваемой компьютерной сети связи, управляемой протоколом случайного множественного доступа.

ИПВ

а

X

A ⁽ x )

B ⁽ x )

Схема функционирования немарковской RQ-системы

Введем обозначение i ( t ) - число заявок в ИПВ в момент времени t.

Так как случайный процесс i ( t ) для рассматриваемой RQ-системы является полумарковским, а эргодические свойства полумарковского процесса полностью определяются эргодическими свойствами его вложенной цепи Маркова, то для рассматриваемого процесса i ( t ) определим его вложенную цепь и выполним исследование ее эргодических свойств.

Рассмотрим моменты времени t1 < t2 < t 3<... < tn < tn+1 <..., где tn - момент окончания режима функционирования прибора завершением обслуживания или этапа оповещения о конфликте, и освобождением прибора; тогда процесс vn = i(tn) с дискретным временем n является вложенной цепью Маркова для полумарковского процесса i(t).

Найдем переходные вероятности

P_A = P { ^v n _{+ 1} = A v n = i } вложенной цепи Маркова v _n .

За один шаг возможны следующие переходы цепи Маркова из состояния vn = i в состояния vn + 1 = J, где J = {i-1,i,i +1,i + 2,i + 3,i + 4,... } . Определим собы тия, соответствующие этим переходам:

• -    i ^ i - 1: на прибор поступила заявка из ИПВ, обслуживание которой завершилось успешно;

• -    i ^ i : на прибор поступила заявка из внешнего потока, обслуживание которой завершилось успешно; или на прибор поступила заявка из ИПВ, но ее обслуживание прервалось заявкой из ИПВ, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого других заявок из внешнего потока не поступало;

• -    i ^ i + 1: на прибор поступила заявка из внешнего потока, ее обслуживание прервалось заявкой из ИПВ, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого других заявок из внешнего потока не поступало; или на прибор поступила заявка из ИПВ, ее обслуживание прервано заявкой из внешнего потока, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого других заявок из внешнего потока не поступало; либо на прибор для обслуживания встала заявка из ИПВ, ее обслуживание прервалось заявкой из ИПВ, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого из внешнего потока поступила одна заявка;

• -    i ^ i + k , к = 2, да : на прибор поступила заявка из внешнего потока, ее обслуживание прервано заявкой из внешнего потока, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого из внешнего потока поступило k - 2 заявки; либо на прибор поступила заявка из внешнего потока, ее обслуживание прервалось заявкой из ИПВ, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого из внешнего потока поступила k - 1 заявка; или на прибор поступила заявка из ИПВ, ее обслуживание прервано заявкой из внешнего потока, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого из внешнего потока поступала k - 1 заявка; либо на прибор поступила заявка из ИПВ, ее обслуживание прервалось заявкой из ИПВ, произошел конфликт и на приборе начался этап оповещения о конфликте, за время которого из внешнего потока поступило k заявок.

^{( X} x )

Пусть P { A _n = k| x } = к j e - условная вероятность того, что на интервале оповещения о конфликте поступит к заявок при условии, что средняя продолжительность этапа оповещения о конфликте равна x [4].

Так как x есть значение случайной величины с функцией распределения A(x), то усредняя по x, получим значение безусловных вероятностей f (к) = J ^^xr- e dA (x).

0 Л •

Тогда, учитывая описание модели, запишем вероятности P ij переходов цепи Маркова v n в виде

P . - х = /" B * ( Х + ( i - 1) а ) ,

Х + г а

Y i >  0 ( i >  N ),

тогда цепь Маркова неэргодична.

Обозначим b - среднее значение времени обслуживания в рассматриваемой RQ-системе, т. е.

Pi =         а ⁽‘ Г 1)а [ 1 - B ’ ( X + ( i - 1) а ) ] ^х

X + i аХ + (i -1) а1-                   J х f (0)+т-Х— B ’ (X+iа);

X + i а

от b = JxdB(x),

P. .=——i— ii + 1 А • А

X + i аX + i а

') ] f (0) +

i а

X

+---

X + i а X + ( i - 1) а

[ 1 - B * ( X + ( i - 1) а ) ] f (0) +

+

⁽ i ^- 1) ^а

X + i а X + ( i - 1) а

P . ,=^" ii + к а «а •

X + i а X + i а

[ 1 - B * ( X + ( i - 1) а

;

') ] f ( к - 1) +

i а

X

+---

X + i а X + ( i - 1) а

^{[ 1 -} B (^X + ⁽ i ^- 1) ^а) ] ^{f (} к ^- 1) +

i а ( i - 1) а

X + i а X + ( i - 1) а

X X

[ 1 - B * ( X + ( i - 1) а ) ] f ( к ) +

+--1 1 - B ( Х + .

X + i а X + i а L от

I P i + к = 1, к =- 1

■)] f ( к - 2);

от где (2) - условие нормировки, а B* (а) = Je-аxdB (x) -0

преобразование Лапласа-Стилтьеса функции распределения B ( x ) .

Таким образом, в явном виде записаны значения переходных вероятностей P ij для вложенной цепи Маркова v n .

Применяя условие Каплана и теорему Сеннота, найдем условия неэргодичности построенной цепи Маркова.

Обозначим zi "Ij

Ф , ( z ) =-----------,                   (3)

1 - z от

Yi=K ^{j -} i ) P ij .              ⁽⁴⁾

j = o

а a - среднее значение продолжительности этапа оповещения о конфликте в рассматриваемой RQ-системе, т. е.

от а =J xdA (x).                (8)

Отметим свойство преобразования Лапласа-Стилтьеса B* (а), заключающееся в выполнении предельного равенства lim aB* (а) = B (0),              (9)

а^от v 7       v 7

где величина B '( 0 ) = B '( x )| x = 0 - значение производной в нуле от функции распределения B ( x ).

Докажем следующее утверждение.

Теорема 1. Цепь Маркова, переходные вероятности которой определяются равенствами (1), является неэргодической при любых значениях загрузки р = X b > 0.

Доказательство. Неравенство (5), сформулированное в условии Каплана, перепишем в виде

Ф/(z) = zi-IPjz >-(1 -z)B.(10)

Найдем предельные при i ^ от значения коэффициентов при степенях z :

lim Pu-X = 0, lim Pii+к = f (к), к = 0,от.(11)

i ^от

Тогда, учитывая предельные неравенства (11) при i ^ от , неравенство (10) примет вид

0 >-(1 - z) B,(12)

который выполняется для любых значений c <  z < 1 и значений параметров системы, в том числе и для любых значений параметра р .

Перепишем неравенство (6), сформулированное в теореме Сеннота, в следующем виде:

от

I ( j - i ) P j j = 0

B (^{X + (} i ^- 1) ^а) + X + i а

Условие Каплана. Если существует положительная константа B , положительное целое число N , и 0 <  z < 1, такое, что

от + I к к = 0

i а ( i - 1) а X + i а X + ( i - 1) а

{ 1 - B * ( X + ( i - 1) а ) } х

V i ^{( z} ) > ^- B

для всех i >  N и c <  z < 1, то будем говорить, что выполнено условие Каплана (5).

Теорема Сеннота. Если для цепи Маркова выполняются условия Каплана (5), у i < от ( i >  0) и существует такое N , что

^X f ( к ) + ^х 7 / а X+b^X { 1 - B* ( X + i а ) } f ( к - 1) + (13)

⁺ . i ^а 7— p _n { 1 ^- B ^{(X + (} i ^- !) ^а) } ^{f ( к -} !) ⁺

X + i аX + ( i - 1) а¹                   '

+ X--|1 - B. (x + i а )) f ( к - 2) 1 >  0.

X + i аХ + i а^{1       (       )J}         I

Найдем предел при i → ∞ выражения (13), учитывая свойство преобразования Лапласа–Стилтьеса (9), получим неравенство

∞

∞

lim∑(j-i)Pij =λxdA(x) =λa>0, i→∞ j=0                   0

которое выполняется для любых значений параметров системы, в том числе и для любых значений параметра ρ .

Из выполнения предельных неравенств (12) и (14) следует существование такого натурального числа i 0 , что для всех i > i 0 выполняются допредельные неравенства (10) и (13).

Таким образом, выполнение условия Каплана и теоремы Сеннота доказывает сформулированную теорему.

Теорема доказана.

Итак, в немарковской RQ-системе с конфликтами заявок и оповещением о конфликте стационарного режима не существует при любых значениях ρ, что доказывает неустойчивое функционирование рассматриваемой компьютерной сети случайного доступа.