Нейро-итерационный алгоритм томографической реконструкции распределенных физических полей в волоконно-оптических измерительных системах

Измерительные устройства являются неотъемлемой частью многих современных технических систем, обеспечивая качество их функционирования и надежность. Наряду с развитием методов измерения сосредоточенных физических параметров в последнее время возрастает интерес к системам регистрации распределенных физических полей (температурных, деформационных и др.). Один из перспективных подходов к решению этой задачи связан с применением методов волоконно-оптической томографии, где восстановление информации о параметрах физических полей выполняется по данным, снимаемым с волоконнооптических измерительных линий, уложенных в соответствии с выбранной схемой сканирования [1].

В традиционной постановке задача реконструктивной вычислительной томографии сводится к восстановлению функции x ( h 1 ,., h_r ) нескольких переменных (2 <  r <  3) по известным интегралам от неё вдоль некоторых траекторий ф в пространстве ( h ,.., h_r ) (как правило, вдоль прямых) [2]:

I ф.1                                                              ______________ y (i) = J x (ф, (L)) dL ; i = 1, m ,                  (1)

где m - число интегральных проекций, ф, ( L ) и | ф _; | - путь и длина траектории сканирования соот ветственно, представляющие i -ю проекцию.

Одна из основных сложностей практического решения задач реконструктивной томографии состоит в ограниченном числе проекций m, недостаточном для однозначной реконструкции ф ункции пространственного распределения исслед уемой величины x(•). В случае оптоволоконной томографии, где каждая проекция y(i) требует физической реализации в виде соответствующим образом уложен- ной волоконно-оптической линии, эта проблема стоит особенно остро.

В таких условиях эффективно применение вычислительных методов, позволяющих учитывать априорные знания о характере реконструируемой функции пространственного распределения физического поля. Один из таких подходов базируется на мощных аппроксимирующих способностях аппарата искусственных нейронных сетей. Настоящая работа посвящена экспериментальному исследованию этого подхода, а также разработке приемов, устраняющих основные недостатки, связанные с его применением.

1. Краткий обзор методов вычислительной томографии

Методы реконструкции, применяемые в вычислительной томографии, можно разделить на интегральные и алгебраические. В интегральных методах реконструируемая функция пространственного распределения рассматривается в непрерывном виде. При этом основным математическим инструментом является аппарат преобразований Радона [2, 3].

В алгебраических методах реконструируемое пространственное распределение рассматривается как дискретная функция, т.е. функция, представленная конечным набором точек, в которых осуществляется реконструкция. Это семейство методов имеет более широкие возможности для использования априорной информации [2], поэтому остановимся на нем подробней.

В классической постановке дискретная форма записи задачи реконструкции сводится к решению системы линейных алгебраических уравнений (СЛАУ) [2]:

Ax = У , (2) где xT = (x1, x 2, .., x„) - вектор-столбец, состоя -щий из n точек искомого пространственного распределения, yT = (y1, y2, ..., ym) - вектор-столбец результатов измерений (показания с m измерит ель- ных линий), A = (ai j; i = 1, m; j = 1, n) - матрица, элемент ai, j которой описывает вклад j-й компоненты xj в i-e измерение yi .

Для решения получаемых СЛАУ используются итерационные алгоритмы как известные в вычислительной математике, например, метод простой итерации или скорейшего спуска [4], так и специально разработанные для целей вычислительной томографии [5-7], в которых учитывается специфика получения проекционных данных.

Среди алгоритмов второй группы одним из наиболее популярных является метод ART (Algebraic Reconstruction Technique), для которого разработано много модификаций [6]. В первоначальном варианте метода ART на каждой итерации последовательно для каждого проекционного значения y_i вычисления проводят по формуле

T ( k )

x ⁽ k ^{+ 1)} = x ^{( k} ) + y i a i x a i ; i = 1, m ,                (3)

aiTai где x(k) и x(k+1) - k-e и (k+ 1)-e приближение к решению           СЛАУ           соответственно, aT = [(ai )1, (ai )2, ..., (ai)n ] - i-я строка матрицы A, записанная в виде вектора-столбца.

Таким образом, для каждого проекционного значения yi соразмерно невязке yi - a ^T x ^{( k} ) и элементам вектора a _i корректируются только те компоненты вектора x , которые участвовали в образовании этого значения y_i . Поскольку матрица А является сильно разреженной, просмотр только линии проецирования значительно сокращает количество выполняемых операций . Ограничения, накладываемые на максимальные и минимальные значения компонентов вектора х , приводят к методу ART2.

Среди других модификаций метода ART интересен мультипликативный вариант – MART [7]. В этом методе все компоненты начального приближения x ⁽⁰⁾ >  0, а итерации имеют следующий вид:

к g

( к + 1) I yi | ( к ) - ,            ■ 1

x j -Нлй" I X j ; ¹ = 1, m ; j = 1, n ,        (4)

j        ( a T x(k) ) j где g = 1, если j-я компонента xj входит в i-e измерение yi, и g = 0 в противном случае.

На вариант метода MART с ограничениями будем ссылаться как на MART2 (по аналогии с ART2).

В качестве сигнала к завершению процед уры оптимизации может использоваться условие:

( y ^{( к} ) - Ax ^{( к} ) )^T( y ^{( к} ) - Ax ^{( к} ) ) <£ ,                     (5)

учитывающее квадратичную величину невязки е .

При реконструкции функ ций пространственного распределения по неполным проекционным данным получаемая СЛАУ оказывается недоопределенной. С практической точки зрения, это означает, что од- ному и тому же вектору проекционных данны х y в общем случае соответствует бесконечное число функц ий пространственного распределения x:

Ax 1 = Ax 2 = „. = Ax = y , где x 1 ^ x 2 ^ „ . ^ x .

Однако если известно, что все ф ункции x принадлежат одному классу, ограниченному множеством X так, что для Vx е X существует единственное обратное преобразование x = G(У), (6) то однозначная реконструкция ф ункций этого класса теоретически возможна с любой заданной точностью. В таких условиях важную роль играет возможность учета на этапе реконструкции априорны х знаний о характере ф ункции x, выраженных в виде признаков, ограничивающих множество решений X. В рамках традиционных методов вычислительной томографии выявление и аналитическая формализация этих признаков может представлять нетривиальную задач у.

В существенной степени лишены отмеченного недостатка нейросетевые методы реконструкции, получившие распространение в последнее время [8-10]. Этот подход подразумев ает прямую реализацию преобразования (6), получаемую путем об учения искусственной нейронной сети (ИНС) на примерах функций x , ограниченных классом X , и соответствующих им проекций y , снимаемых с реальной измерительной системы.

С нейросетевым подходом связаны три принципиальных недостатка.

• •    Потребность в большом числе обучающих примеров, необходимых для плотного покрытия всего множества функций класса X. Выполнение этого требования на практике может оказаться затруднительным по причинам существенных трудозатрат на эксперимент, отсутствия возможности осуществления контролируемого активного воздействия на диагностируемую конструкцию, недопустимостью ее вывода в аварийные режимы функционирования и т.д.

• •    Необходимость обучения ИНС для каждой отдельно взятой измерительной системы, об условленная слабой переносимостью синтезированных нейросетевых алгоритмов реконструкции с одной аппаратной платформы на друг ую.

• •    Отсутствие гарантий удовлетворительного качеств а при реконструкции функций, не принадле-жащ их классу X. Прич ем в этом случае результат реконструкции не то лько может о тлич ать ся существ енными ошибками, но и, как правило, не удов-летво ря ет исходной системе уравнений (2), по -скольку это требов ание в яв ном вид е в нейросетевом решении отсутствует.

2.    Нейро-итерационный алгоритм реконструкции

• 3.    Распространение метода MART на случай мультипликативного типа нелинейности системы алгебраических уравнений

Предлагаемый в настоящей работе алгоритм реконструкции направлен на устранение отмеченны х недостатков нейросетевого подхода. Он основан на широком использовании математической модели измерительной системы и совместном применении нейросетевого и алгебраического подходов, где первый учитывает априорные знания, используется для выбора начального приближения решения, а второй обеспечивает соответствие решения исходной системе алгебраических уравнений. Схему предлагаемого нейро-итерационного алгоритма реконструкции (НИАР) иллюстрирует рис. 1.

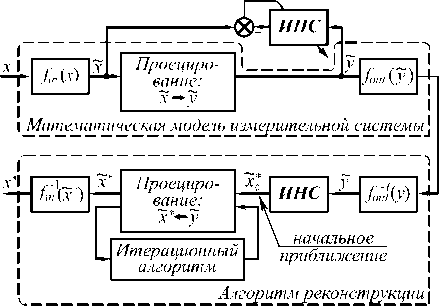
Рис. 1. Блок-схема нейро-итерационного алгоритма реконструкции

Алгоритм реконструкции в представленной схеме рассматривается как инверсная реализация математической модели измерительной системы (информация распространяется в обратном направлении). Здесь функции f_in ( • ), fu ( • ) и их инверсные реализации f ^(0, f_o ^0 учитывают передаточные характеристики отдельных измерительных преобразователей (функции с индексом " in ") и измерительных каналов целиком (функции с индексом " out "). Кроме того, с помощью этих функций выполняется нормирование данных х и у , относительно которых в НИАР выполняется основная часть вычислений. Обучение ИНС на модельных данных снимает необходимость проведения большого числа натурных экспериментов, а его выполнение на примерах нормированных данны х снижает зависимость нейросетевого решения от аппаратной платформы, на которой эти данные были получены. Дополнительную эффективность этот прием приобретает в случае нелинейности функций f_in ( • ), f_out ( • ), поскольку в этом случае дополнительно достигается упрощение используемых структур ИНС и сокращение вычислительных затрат итерационного алгоритма.

В качестве итерационной части в предлагаемом решении может применяться любой итерационный алгоритм, допускающий возможность использования начального приближения. Здесь необходимо отметить, что активизация итерационной части НИАР может выполняться только в том случае, если результат нейросетевой реконструкции оказывается неудовлетворительным, т.е. не выполняется условие (5), что может произойти в случае реконструкции функций, чей класс отличается от используемого при обучении ИНС.

В оптоволоконной томографии могут встречаться задачи, где воздействия на измерительную линию не суммируются (непрерывно интегрируются), а дискретно перемножаются. В частности, такая ситуация возникает при установке на оптоволоконной линии измерительных преобразователей с амплитудной модуляцией [11]. В этом случае система уравнений, описывающая задачу реконструкции , принимает нелинейный вид:

n

П xa¹ = У, ; i = 1, m ,                           (7)

• j = 1

где A = ( a_u ; i = 1, m ; j = 1, n ) - матрица, элемент a_{i 1} = 1, если 1 -я компонента x₁ входит в i -e измерение y_i , и a_i1 = 0 в противном случае. Для удобства дальнейшего изложения введем оператор H { • }, реализующий нелинейное отображение у = H { х }.

Распространение метода MART на случай решения систем нелинейных алгебраических уравнений вида(7) приводит к формуле:

( У.  ) g ™     — x4 = -----i x4 ; i = 1, m; 1 = 1, n,(8)

• 1       (H{x(k)}i J 1                 7v v

4.    Описание лабораторной установки

где y_i - i -й элемент вектора измерений у , H { x ⁽ k ) } _i -расчетное значени е y_i относительно текущего решения x ⁽ k ) , g = 1 h , если a_{i 1} = 1, в противном случае g = 0, h - число компонент x , участвующих в формировании i -го измерения y_i .

Таким образом, если в линейном варианте MART (4) все компоненты вектора х , аддитивно участвующие в образовании проекции y_i , корректируются кратно относительной ошибке, то в нелинейном варианте (8), имеющем мультипликативную форму, корректировка выполняется пропорционально корню степени h из этой ошибки. В обоих случаях после каждой i -й корректировки достигается равенство фактически измеренной проекции y_i и ее расчетного значения H { х ⁽ k ^{+ 1)}} _i .

Экспериментальная часть работы выполнена на примере лабораторного макета оптоволоконной системы измерения распределенного температурного поля. Его внешний вид представлен на рис. 2. Лабораторная установка содержит 16 оптоволоконных измерительных преобразователей, совмещенных на общих стойках с контрольными термометрами и нагревательными элементами, имитирующими матрицу распределения температурного поля размером 4 х 4 . В качестве нагревательных элементов в установке использованы лампы накаливания, потребляемая мощность кото- рых регулируется задающим устройством, управляемым с помощью персонального ко мпьютера [12].

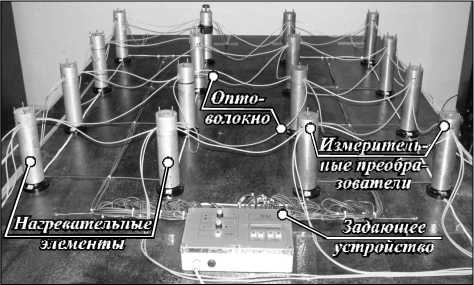
Рис. 2. Внешний вид макета измерительной системы

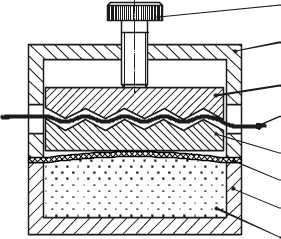
Конструкция используемых в работе оптоволоконных измерительных преобразо вателей изображена на рис. 3. В ее основу положен эффект преобразования давления, вызванного температурным увеличением объема рабочей жидкости (вода) в герметичной камере, в механическую деформацию оптоволокна.

Регулиро «очный винт

Крышка

Верхний поршень Оптоаолокио

Нижний поршень

Мембрана

Камера

/ \юочая жидкост ъ

Рис. 3. Конструкция измерительного преобразователя

Прохождение светом участков оптоволокна с малым радиусом изгиба связано с нарушением эффекта полного отражения, что приводит к потере мощности оптического излучения и уменьшению амплитуды оптического сигнала, регистрируемого на выходе [13]. В рассматриваемой конструкции эти потери прямо пропорциональны температуре рабочей жидкости (рис. 4).

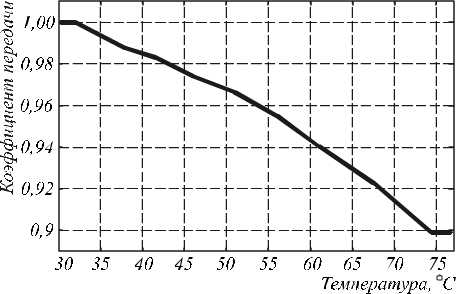
Рис. 4. Пример передаточной характеристики

Экспериментальный о браз ец измерительного преобразователя позволяет регистрировать температуру в диапазоне от 32 до 74,5°C. Подробней озна- комиться с его характеристиками можно по материалам работы [14].

На рис. 5 изо бражен а исследуемая в работе схема объединения оптоволоконных преобразователей в измерительную сеть , содержащую три направления сканирования. В представленной схеме каждая из 15 оптоволоконных измерительных линий последовательно охватывает от одного до четырех измерительных преобразователей.

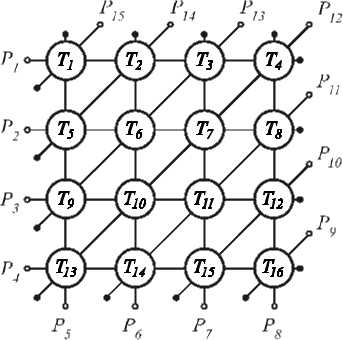
Рис. 5. Схема измерительной сети

Математическое описание измерительной системы представляется системой нелинейных алгебраических уравнений (9) [11]

' P 1 = к • И Т) • f-. х Т • f x з ( Т з ) • f 4 х(ТУ;

р_г = к ₂ • f. 5 (T ) • f 6 _;( T ) • f 7 7 (Т , ) • f 88 (T );

Р з = к 3 • f s> (T9) • №) • f li ( T li ) • fx 2 (T 12 );

j                  -                          (9)

P 13 = k i3 • f 3 з ( Тз) • f 66 (T₆) • f ss (T9);

P 14 = k 14 • fx2<ТД • f_tx(T5);

P15 = ki5 • fx(Tx), где Pi – значение мощности оптического сигнала, регистрируемое на выходе i-й измерительной линии , ki – коэффициент усиления i-й измерительной линии, учитывающий исходно введенную в оптоволокно интенсивность оптического излучения и коэффициент усиления измерительного канала, Tj и fj (•) - температура и передаточная характеристика j-го измерительного преобразователя соответственно .

В терминах вычислительной томографии реше ние системы уравнений (9) относительно входящих в нее температур T 1 …T 16 представляет задачу ре конструкции функции пространственного распреде ления температурного поля по неполным проекци онным данным [2]. Сложность аналитического ре шения этой задачи обусловлена тем , что число неиз вестных системы (9) больше числа уравнений , что переводит ее в разряд некорректных [15].

5.    Модели измерительной системы

Нелинейная модель. На рис. 6 представлена структурная схема математической модели измерительной системы, построенная в соответствии с ее аналитическим описанием (9), расширенным введением шума и добавлением блоков квантования по уровню, учитывающих наличие на выходе реальной системы 12-ти разрядных аналого-цифровых преобразователей. Коэффициенты усиления к1... к 15 и индивидуальные передаточные характеристики измерительных преобразователей f1.. f1 6 выявлены экспериментально (последние аппроксимированы степенными полиномами четвертого порядка).

Дз Д Д* Дз Д1 Д До Д

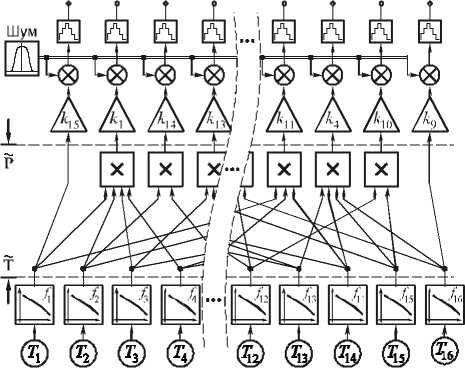
Рис. 6. Структурная схема математической модели измерительной системы

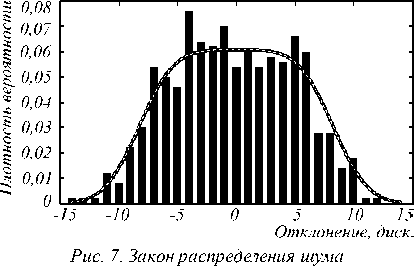
Закон распределения шума получен путем обобщения данных по всем измерительным линиям при одновременном воздействии на все измерительные преобразователи. На рис. 7 представлены экспериментальные данные и результат их аппроксимации . По оси абсцисс на этом графике отложена разница межд у фактическими и модельными результатами, оцениваемыми в дискретах аналогово-цифрового преобразователя (1 диск. = 0,12 ° C). Аппроксимированный закон распределения получен как сумма шумов с нормальным (дисперсия о ² = 2,34) и равномерным ( о ² = 22,4) законами распределения при математическом ожидании ц = 0 .

Линеаризованная модель. Для возможности применения классических алгебраических методов реконструкции в отношении нелинейной задачи (9) выполним ее линеаризацию. Перепишем систему уравнений (9) относительно линеаризованных потерь мощности оптического излучения, возникающих при прохождении светом отдельных измерительных преобразователей, полагая, что эти потери суммируются:

c - Ax = y , (10) где x ^T = ( T i ,T 2 ,., Т б ), y ^T = ( p , P 2 , .., 7 15 ), A — матрица коэффициентов потерь, c ^T = ( c 1 , c ₂, ..., cm ) - вектор-столбец смещений, элементы которого найдем из условия:

c = y + A x|

x = (32, 32, ., 32)^T ’

где 32 ° C - нижняя граница диапазона чувствительности используемых конструкций измерительных преобразователей (рис. 4), обширно представленная в исслед уемых далее распределениях.

6.    Исследуемые функции пространственного распределения температурного поля

В работе исслед уются четыре класса ф унк ций распределений температурного поля, которые условно обозначены как точечное, полиномиальное, радиальное и конусное. Их краткое описание и характеристики представлены в табл. 1. По критерию дифференцируемости эти распределения принадлежат к различным классам, что и обусловило их выбор.

Таблица 1. Исследуемые распределения

Обозначение	Краткое описание ф ункции пространственного распределения температурного поля	Отличительная особенность
Точечное	Произвольное температурное воздействие на заданном числе измерительных преобразователей	Дискретная, не диффе-ренцируе-мая функция
Полино-миаль-ное	Основу ф ун кции составляют два степенных полинома пятого порядка, регламентирующих ее развитие в двух взаимно перпендикулярны х направлениях	Функция дифференцируется пять раз, после чего обращается в нуль
Радиальное	В основу ф ункции пространственного распределения положена радиальнобазисная функция T = e~R , где R – евклидово расстояние от текущей координаты до центра ф ункц ии ( R = 0)	Бесконечно дифференцируемая функц ия
Конусное	То же, что радиальное, но в основу положена ф ункция Г 0, - 1 >  R >  1 т ( R ) = 1 V 1 [ 1 - R , - 1 <  R <  1	Функция терпит разрыв по первой производной

• 7.    Экспериментальное исследование методов реконструкции распределенных температурных полей: предварительные замечания

8.    Реконструкция точечных пространственных распределений температурного поля

Во всех последующих экспериментах в качестве нейросетевой части НИАР используются линейные сети, параметризуемые аналитически с помощью метода наименьших квадратов. Этот выбор позволяет снять недостатки, связанные с обучением нелинейных ИНС.

Итерационная часть НИАР построена на основе метода (8), предложенного в разделе 3 настоящей работы. Необходимые в НИАР функции обратны х передаточных характеристик измерительных преобразователей f_i ^{- 1}( ⋅ ) получены путем аппроксимации соответствующих закономерностей степенными полиномами шестого порядка.

Обучение нелинейных ИНС (персептроны), пред ставляющих трад иционный нейросетевой подход к задаче реконструктивной томографии, выполнено с помощью алгоритма Лев енб ерга-Маркв ардт а. Отличительной особенностью н ейро-сетевой реконструкции является то, что она, в отличие от алгеб раических методов, мо жет быть выполнена н езав исимо для отдельных значений функц ии распределения. С целью упрощения численные эксперименты выполнены на примере реконструкции единств енного значения функции распределения - T 10 (рис. 4).

Это упрощение не оказывает принципиального влияния на объективность проведенного исследования, позволяя при этом существенно сократить его время. Для объективности сравнения различных методов реконструкции, рассматриваемы х в работе, этот способ оценки качества применялся во всех численных экспериментах. Для обозначения структур ИНС б удем использовать след ующий формат: [ h ₁ - h ₂ - … - h_n - 1] , где h ₁… h_n – число нейронов в каждом из n скрытых слоев (активационная функция: гиперболический тангенс), 1 – неизменно один нейрон с линейной функцией активации на выходе ИНС.

Для оценки качества реконструкции в исследовании используется среднее (абсолютное) и максимальное отклонение температуры по независимой тестовой выборке, записанные через дробь в форме: среднее / максимальное. Такая комплексная мера, кроме всего прочего, позволяет косвенно оценить картину распределения отклонений.

На первом этапе исследования как обучающие, так и тестовые выборки формируются с помощью нелинейной модели измерительной системы, из которой для чистоты сравнительного эксперимента исключен шум. Все тестовые выборки содержат 5000 примеров функ ций пространственного распределения. Эксперименты с введением шума, а также эксперименты с тестированием на реальных данны х буд ут отмечены отдельно.

Результаты реконструкции фун кций точечных распределений представлены в табл. 2. Тип точечного распределения устанавливает число точек, на которые одновременно оказывается воздействие. Для возможности сравнения в этой таблице также отражены результаты реконструкции, полученные с помощью алгебраического метода MART2, наилучшим образом проявившего себя на рассматриваемом классе ф ункций пространственного распределения.

Из представленной таб ли цы видно, как скачкообразно усло жняется топология ИНС и возрастаю т объемы обучающих выборок уже при переходе от одной до двух точек одновременного воздействия . При этом по лучаемые результаты оказыв аются хуже теоретически ожид аемых (в обоих случ аях система уравнений (9) имеет аналитическое решение [16]) и уступают не только результатам НИАР, но и в большинств е рассмотренных случаев не превосходят результаты классического метода MART2, полученны е на основе линеаризованной модели измерительной системы. Возникшие труд ности обучения ИНС можно объяснить тем, что реализуемый ими класс функций слабо пересекается с классом функций, необходимым для представления решения задачи реконструкции ф ункц ии точечных распределений. Получ енные результаты позво ляют делать вывод о том, что практическое применение нейросетевого апп арат а для целей томографической реконструкции этого класса ф унк ций пространств енного распределения физических по лей неэффективно, ввиду критических трудо затрат на обучение ИНС .

Таблица 2. Результаты реконструкции точечных пространственных распределений температурного поля

Тип точечного распределения	ИНС		НИАР [1] / 5000	MART2
	Погрешность реконструкции	Структура / Выборка
1	0,0025 / 0,22	[5-1-1] / 5000	0,012 / 0,11	0,12 / 3,03
2	0,11 / 2,24	[20-1-1] / 20000	0,019 / 0,16	0,27 / 3,53
3	0,35 / 20,27	[20-1-1] / 20000	0,1 / 16,97	0,51 / 16,18
4	0,87 / 28,12	[15-1-1] / 20000	0,29 / 24,49	0,84 / 22,84
5	1,61 / 31,82	[15-1-1] / 15000	0,82 / 23,18	1,45 / 23,56
7	3,43 / 29,75	[15-1] / 10000	2,09 / 27,56	2,81 / 24,27
10	5,32 / 29,35	[10-1] / 5000	4,39 / 30,79	4,93 / 27,84

Таблица 3. Результаты реконструкции гладких пространственных распределений температурного поля

Пространств енное распределение	ИНС		НИАР [1] / 5000	MART2
	Погрешность реконструкции	Структура / Выборка
Полиномиальное	0,025 / 0,27	[10-1] / 5000	0,19 / 2,31	2,63 / 5,25
Радиальное	0,034 / 0,67	[15-1] / 5000	0,95 / 4,59	2,15 / 6,18
Конусное	0,078 / 0,97	[15-1] / 5000	0,49 / 3,27	2,83 / 5,27

9.    Реконструкция гладких пространственных распределений температурного поля

Представленные в табл. 3 результаты реконструкции гладких ф ункций пространственного распределения как с точки зрения качества, так и с точки зрения сложности обучения ИНС принципиально отличается от результатов реконструкции ф ункци й точечных распределений. Здесь реализуемый ИНС тип нелинейности позволяет более эффективно учесть априорные признаки реконструируемого класса ф ункци й, чем это достигается при использовании линейных сетей, применяемых в НИАР. Обратим внимание, что точность реконструкции НИАР в случае использования в его структуре нелинейных ИНС оказывается соизмеримой с достигаемой в рассматриваемых экспериментах с помощью традиционного нейросетевого подхода.

10.    Обобщающие свойства исследуемых решений

До настоящего момента в работе рассматривались случаи, где качество реконструкции обучаемых алгоритмов (ИНС и НИАР) исследовалось на примерах ф ункций пространственного распределения температурного поля того же типа, что использовался при их обучении. В табл. 4 представлены результаты тестирования ранее синтезированных решений на примерах различных типов ф ункций распределения (ячейки таблицы, отмеченные серым цветом, дублируют результаты табл. 2 и 3). По представленным данным видно, что при тестировании рассматриваемых решений на типах ф ун кций пространственного распределения, отличных от используемых при их обучении, снижение качества реконструкции регистрируется в обоих случаях. Однако в случае НИАР это снижение оказывается ниже, а итоговое качество реконструкции – выше, чем достигаемое при использовании исключительно нелинейных ИНС.

Недостаток информации при решении исходно недоопределенной задачи реконструкции компенсируется априорными знаниями о классе реконструируемых функций пространственного распределения физического поля. Чем больше объем этих знаний, тем меньше неопределенность и выше качество реконструкции. В случае нейросетевой реконструкции эти знания «впитываются» ИНС в процессе ее обучения. Их распространение на другие классы функций пространственного распределения, для которых эти знания ложны, наоборот, может привести к появлению дополни- тельных ошибок. Наличие в НИАР итерационной части, приводящей в случае необходимости реализуемое нейронной сетью начальное приближение решения к его соответствию исходной системе алгебраических уравнений (в данном случае (9)), существенно снижает этот недостаток. Не вошедшие в настоящее изложение эксперименты показали, что на примерах гладких функций пространственного распределения, представленных в табл. 4, итерационная часть НИАР в среднем снижает среднее и максимальное отклонение на 37% и 44% соответственно. Таким образом, в режиме обобщения НИАР на базе линейных нейросетей превосходит результаты, получаемые в этих же условиях с помощью исключительно нелинейных ИНС.

11.    Влияние шума на качество реконструкции

В табл. 5 представлены результаты реконструкции зашумленных функций пространственного распределения температурного поля, полученные с помощью различных методов. Характеристики шума и способ его введения в модель рассмотрены в разделе 5 настоящей работы. Для методов, содержащих этап обучения, эксперименты выполнены как для случая обучения на зашумленных данных, так и для случая обучения на примерах без шума. По представленным результатам экспериментов видно, что шум не оказывает критического влияния на качество реконструкции, однако для нейросетевых методов его учет необходим на этапе обучения.

12.    Натурные эксперименты

В заключительной части исследования рассмотрим результаты реконструкции, полученные в реальной измерительной системе (табл. 6). Ввиду того, что формирование тестовых пространственных распределений в реальных условиях требует значительных временных затрат, ограничим их число 20-ю представительными примерами. При этом оценку качества реконструкции выполним по всем 16-ти элементам функции распределения. Это требует обучения 16-ти ИНС для каждого рассматриваемого класса функций пространственных распределений. Обучение выполнено на модельных данных с шумом. Параметры ИНС (топология, объем обучающей выборки) приняты аналогичными выявленным ранее в ходе численных экспериментов для соответствующих классов функций (табл. 2 и 3). В НИАР используются линейные сети, обученные на тех же выборках.

Таблица 6. Результаты натурных экспериментов

Метод реконструкции	Тестовое распределение (20 реальных примеров)
	Точечное 1	Полиномиальное	Радиальное
ИНС	0,54 / 2,63	0,49 / 1,51	0,67 / 2,18
НИАР	0,36 / 1,78	0,62 / 2,93	1,34 / 4,76
MART2	0,51 / 4,26	3,02 / 6,32	2.,49 / 6,98

Таблица 4. Обобщающие свойства исследуемых решений

Тестирование Обучение		Точечное 1	Точечное 3	Полиномиальное	Радиальное	Конусное
Точечное 1	ИНС	0,002 / 0,22	3,54 / 42,37	21,3 / 42,5	14,1 / 41,8	19,4 / 40,6
	НИАР	0,012 / 0,11	0,11 / 17,88	2,12 / 13,68	1,52 / 8,02	0,87 / 7,87
Точечное 3	ИНС	0,068 / 1,56	0,35 / 20,27	18,2 / 40,63	6,76 / 30,96	14,8 / 39,76
	НИАР	0,011 / 0,10	0,10 / 17,07	1,02 / 4,96	1,36 / 5,04	0,91 / 4,33
Полиномиальное	ИНС	2,91 / 15,8	5,39 / 24,96	0,025 / 0,27	1,62 / 8,23	0,7 / 4,2
	НИАР	0,012 / 0,11	0,11 / 18,99	0,19 / 2,31	1,37 / 5,06	0,72 / 3,86
Радиальное	ИНС	1,35 / 5,7	3,45 / 25,64	1,29 / 6,98	0,034 / 0,67	0,67 / 5,1
	НИАР	0,010 / 0,12	0,11 / 19,48	1,04 / 6,88	0,95 / 4,48	0,53 / 4,55
Конусное	ИНС	2,66 / 13,3	5,39 / 35,11	1,77 / 12,7	0,55 / 4,49	0,078 / 0,97
	НИАР	0,011 / 0,11	0,11 / 17,38	0,94 / 6,63	1,01 / 4,54	0,49 / 3,27

Таблица 5. Результаты реконструкции в условиях шума

Метод реконструкции		Тестовое распределение (5000 модельных примеров с ш умом)
		Точечное 1	Точечное 2	Полиномиальное	Радиальное
Обучение без шума	ИНС	4,16 / 60,58	0,68 / 16,31	0,39 / 1,16	0,56 / 2,41
	НИАР	0,26 / 1,52	0,29 / 1,85	0,46 / 2,66	1,13 / 4,89
Обучение с шумом	ИНС	0,19 / 1,77	0,31 / 3,36	0,33 / 0,94	0,39 / 1,41
	НИАР	0,25 / 1,44	0,29 / 1,79	0,47 / 2,62	1,11 / 4,97
ART		2,73 / 11,44	3,86 / 19,09	2,72 / 5,63	2,74 / 8,25
ART2		0,41 / 4,14	0,55 / 4,56	2,76 / 6,09	2,42 / 7,41
MART2		0,4 / 3,96	0,53 / 4,32	2,78 / 5,82	2,3 / 6,79

Результаты натурных экспериментов подтверждают возможность использования математической модели измерительной системы для обучения ИНС. Несколько более высокий уровень регистрируемы х отклонений можно объяснить более сложной природой шума в реальной системе, который в существенной степени связан с эффектом остаточных деформаций оптоволокна.

Заключение

Результаты работы показывают, что качественная реконструкция функций пространственного распределения физических полей по неполным проекционным данным требует учета априорных знаний. Нейросетевой аппарат, благодаря обучению на примерах реальных пространственных распределений, является эффективным и во многом универсальным средством учета этих знаний. Наряду с преимуществами, прове- денное исследование выявило недостатки нейросетевого подхода. К ним можно отнести потребность в большом числе обучающих примеров; высокие трудозатраты на обучение ИНС; низкую способность к реконструкции некоторых классов функций пространственного распределения (в частности, точечных); отсутствие гарантий удовлетворительного качества реконструкции тех классов функций распределения, которые не учитывались на этапе обучения.

Результаты представленных экспериментов демонстрируют, что наиболее эффективно потенциал классического нейросетевого подхода реализуется на примерах реконструкции гладких ф ункц ий пространственного распределения, имеющих стационарный базис. Если эти условия не выполняются, то точность нейросетевого решения в большинстве случаев оказывается ниже, чем точность простых классических методов реконструктивной томографии.

Предложенный в работе нейро-итерационный алгоритм реконструкции во многом лишен отмеченных недостатков. Он основан на широком использовании математической модели измерительной системы и совмещает в себе способность ИНС к учету априорных знаний с надежностью и простотой алгебраических методов.

Благодаря обучению на модельных данных, из которых исключена часть нелинейности измерительной системы, а также наличию итерационной части решения, в предложенном подходе становится возможным использование более простых структур ИНС. При этом применение линейных ИНС, используемых в настоящей работе, не является обязательным условием. Вместе с тем именно этот класс ИНС след ует рекомендовать применять при решении практических задач. Это обусловлено высокими трудозатратами на обучение нелинейных ИНС, имеющих большие размерности входных и выходных векторов, что свойственно задачам реконструктивной томографии и обостряется по мере роста размерности измерительной системы. Детальное обсуждение этой проблемы осталось за рамками настоящего изложения.