Нейро-нечеткие сети

Нечёткой нейронной сетью обычно называют нейросеть, которая построена на основе многослойной архитектуры с использованием И-, ИЛИ-нейронов. При создании гибридной технологии кроме объединения систем по данным можно использовать нейрокомпьютинг для решения частной подзадачи нечётких экспертных систем, а именно настройки параметров функции принадлежности. Функции принадлежности можно сформировать двумя способами: методом экспертной оценки, на основе статистики. Гибридные технологии предлагают третий способ: в качестве функции принадлежности выбирается параметризованная функция формы (напр. гауссова кривая с параметрами а, b), параметры которой настраиваются с помощью нейросетей. Настройка параметров может быть получена в рамках алгоритма обратного распространения ошибки. Таким образом, нечеткая нейронная сеть наряду с классическими нейронами, являющимися пороговыми суммирующими элементами, должна включать в себя И-, ИЛИ-нейроны.

Нечеткие нейроны

Преобразование, осуществляемое типичным нейроном с двумя входами, имеет вид У = f^WHl + W2X2) , где .''■'■-сигмоидная функция. Для того, чтобы обобщить его, нужно представить себе, что вес нейрона не обязательно должен умножаться на значение соответственного входа, а здесь может быть применена какая-либо другая операция. Далее, суммирование воздействий также может быть заменено неким другим действием. Наконец, вместо сигмоидной функции потенциал нейрона может быть преобразован каким-либо новым способом. В нечеткой логике операция умножения заменяется для булевых переменных операцией И, а для числовых -операцией взятия минимума (min). Операция суммирования заменяется соответственно операциями ИЛИ и взятием максимума (max).

Если осуществить соответствующие замены в преобразовании, осуществляемом знакомым нам нейроном, и положить в нем f^") = - (линейный выход), то мы получим так называемый нечеткий ИЛИ-нейрон:

у = max(min(wL, ar 1) min(w₂, £2)}■

Для нечетких нейронов полагается, что значения входов и весов заключены в интервале [0, 1], поэтому и выход нейрона ИЛИ будет принадлежать этому же интервалу.

Используя противоположную подстановку (умножение max), (сложение min ) получим преобразование, характерное для нечеткого И-нейрона:

у = min{max(wi, ari) max(w2,ar₂)}

ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. Она была предложена Янгом (Jang) в начале девяностых. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. ANFIS реализует систему нечеткого вывода Сугено в виде пятислойной нейронной сети прямого распространения сигнала. Назначение слоев следующее:

первый слой - термы входных переменных;

второй слой - антецеденты (посылки) нечетких правил;

третий слой - нормализация степеней выполнения правил;

четвертый слой - заключения правил;

пятый слой - агрегирование результата, полученного по различным правилам.

Входы сети в отдельный слой не выделяются. На рисунке ниже изображена ANFIS-сеть с двумя входными переменными (x1 и x2) и четырьмя нечеткими правилами. Для лингвистической оценки входной переменной x1 используется 3 терма, для переменной x2 - 2 терма.

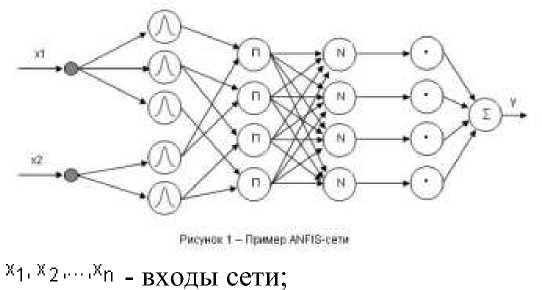
y - выход сети;

I R_r : Если Ki = ai _r ии x_n = a_{n r}, to v = bn _r + bi _rxi + ... + b_{n r}x_n                  „

- нечеткое правило с порядковым номером r;

m - количество правил , r = 1,m ;

ai,r - нечеткий терм с функцией принадлежности l^i) , применяемый для лингвистической оценки переменной xi в r-ом правиле ( r = 1,m ,i- 1,n);

bq,r - действительные числа в заключении r-го правила ( r = 1,m , q = O,n ).

ANFIS-сеть функционирует следующим образом.

Слой 1. Каждый узел первого слоя представляет один терм с колокообразной функцией принадлежности. Входы сети K-J.x?....^соединены только со своими термами. Количество узлов первого слоя равно сумме мощностей терм-множеств входных переменных. Выходом узла являются степень принадлежности значения входной переменной соответствующему нечеткому терму:

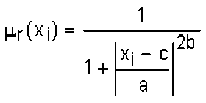
, где a, b и c - настраиваемые параметры функции принадлежности.

Слой 2. Количество узлов второго слоя равно m. Каждый узел этого слоя соответствует одному нечеткому правилу. Узел второго слоя соединен с теми узлами первого слоя, которые формируют антецеденты соответствующего правила. Следовательно, каждый узел второго слоя может принимать от 1 до n входных сигналов. Выходом узла является степень выполнения правила, которая рассчитывается как произведение входных сигналов. Обозначим выходы узлов этого слоя через ^Tr , r = 1,m .

Слой 3. Количество узлов третьего слоя также равно m. Каждый узел этого слоя рассчитывает относительную степень выполнения нечеткого правила:

.

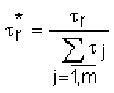
Слой 4. Количество узлов четвертого слоя также равно m. Каждый узел соединен с одним узлом третьего слоя а также со всеми входами сети (на рис. 1 связи с входами не показаны). Узел четвертого слоя рассчитывает вклад одного нечеткого правила в выход сети:

Уг =^r (boj +biirx1 +... + bnrxn) .

Слой 5. Единственный узел этого слоя суммирует вклады всех правил:

• У = У1 + .y_r- + Ут

  .