Нейронечеткие системы в моделировании устройств беспилотных транспортных средств

Математическая теория нечетких множеств (fuzzysets) и нечеткая логика (fuzzylogic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским уче-

Золкин Александр Леонидович доцент кафедры информатики и вычислительной техники. Поволжский государственный университет телекоммуникаций и информатики, город Самара. Сфера научных интересов: автоматика и автоматизация; информатика и вычислительная техника; прикладная информатика; программирование; транспорт. Автор 300 опубликованных научных работ.

ным Лотфи Заде (Lotfi Zadeh) в 1965 году. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Рассматривается процесс организации персептрона, производится программный расчет и определяется функциональная роль адаптивной нечеткой системы в кибернетическом и вычислительном аспектах. Однако основным их недостатком является необходимость в привлечении экспертов исследуемой области для формирования правил и функций принадлежности. Именно поэтому было решено совместить нечеткие системы с нейронными сетями, обладающими хорошими обучающими возможностями, но которым не хватает способности к интерпретации. В результате появились нейронечеткие системы, которые стали довольно мощным инструментом для работы с нечеткими множествами [2; 3; 5; 6; 11].

Методы исследования

Наибольшее распространение в настоящее время получила архитектура нейронечет-кой системы ANFIS, в который вывод осуществляется на основе аппарата нечеткой логики, а параметры функций принадлежности настраиваются с использованием метода обратного распространения ошибки [4].

Нейронечеткие системы в моделировании устройств беспилотных транспортных средств

Результаты исследования

ANFIS (adaptive neuro-fuzzy inference system) – адаптивная сеть на основе системы нечеткого вывода Такаги – Сугено. Данная система соответствует набору нечетких правил IF-THEN, которые обладают способностью к обучению для аппроксимации нелинейных функций [7; 9]. Общая форма модели вывода Такаги – Сугено может быть представлена следующим образом [8; 12]:

ЕСЛИ x 1 это A1 И x2 это A2 И .... И xn это An, ТО y = f(x 1,x2,.,xn).(1)

Правила вывода Такаги – Сугено для нейронечеткой сети, изображенной на Рисунке 1, будут выглядеть следующим образом:

ЕСЛИ x 1 это A1 И x2 это B1, ТО y = f(x 1,x2);(2)

ЕСЛИ x 1 это A2 И x2 это B2, ТО y = f (x 1,x2).(3)

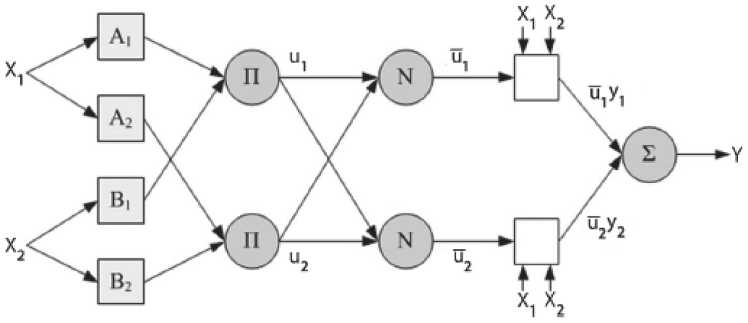
Рисунок 1. Блок-структура адаптивной нейронечеткой системы вывода (ANFIS)

Первый слой является слоем фаззификации, роль которого – установить соответствие между численными значениями входных переменных системы нечеткого вывода и значениями функций принадлежности соответствующих им термам лингвистических переменных. Лингвистическая переменная – это переменная, которая может принимать значения фраз из естественного или искусственного языка.

Например, лингвистическая переменная «скорость» может иметь термы «высокая», «средняя», «очень низкая» и др. Таким образом, каждый нейрон на первом слое в качестве функции активации содержит функцию принадлежности, определяющую степень, с которой входы соответствуют всем своим термам. Степени принадлежности каждой функции вычисляются с использованием набора параметров предпосылки { a , b , c }. В качестве функции принадлежности может быть выбрана, к примеру, гауссова функция

g(x) = ae (x 2b) ,(4)

2c где a – максимальная высота; b – сдвиг пика от 0; с – ширина колокола.

Однако так как значения функции принадлежности должны изменяться в диапазоне от [0; 1], то параметр a всегда будет равен 1.

Второй слой обозначается как «слой правил», так как количество нейронов на нем равно количеству правил системы. Каждый узел второго слоя соединен только с теми узлами первого слоя, которые формируют посылки соответствующего правила. Результа- том слоя являются антецеденты (посылки) нечетких правил, другими словами, выходом каждого узла будет являться степень истинности текущего правила. Данная степень определяется как логическое произведение (минимум) от множества степеней принадлежности по формуле ui = µAi(x1)*µBi(x2), i = 1…m.

Пример выполнения данного произведения для двух входов и двух правил для каждого входа представлен на Рисунке 2.

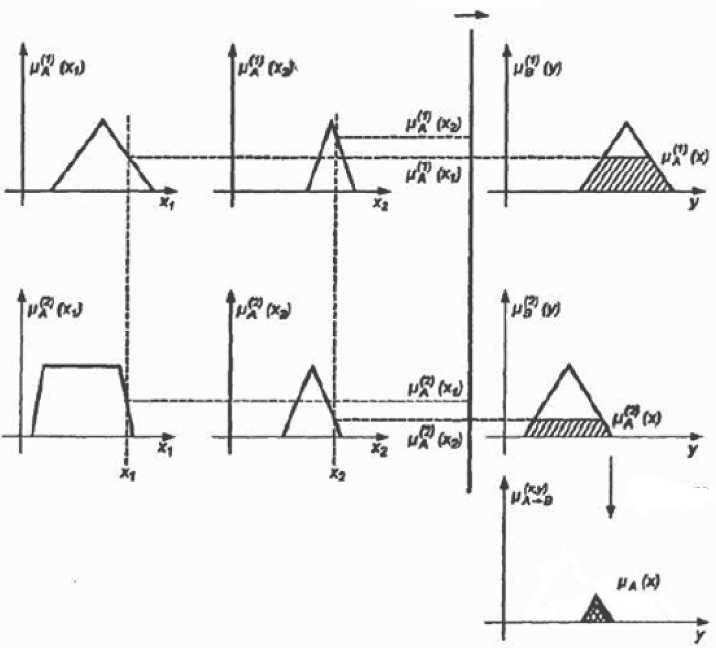
Рисунок 2. Определение степени истинности правил

Процесс обучения сети выполняется итерационно. Каждая итерация состоит из двух этапов. На первом этапе при помощи обучающей выборки находятся оптимальные параметры заключений четвертого слоя с помощью метода наименьших квадратов, после чего с помощью метода обратного распространения ошибки изменяются параметры предпосылок. Данная процедура выполняется до тех пор, пока ошибка не уменьшается до требуемого значения.

Для лучшего понимания принципа работы нейронечеткой системы ANFIS будет рассмотрен пример обучения сети с нуля.

Так как данный вид нейронечеткой системы обладает хорошей аппроксимационной способностью нелинейных функций, то в качестве обучающей выборки будут приняты параметры функции от двух переменных и ее результат.

Обзор отечественных и зарубежных источников литературы показывает, что одним из перспективных направлений развития искусственного интеллекта является комбинирование технологий с целью получения новых алгоритмов машинного обучения [1; 10]. Так,

Нейронечеткие системы в моделировании устройств беспилотных транспортных средств комбинирование теории нечетких множеств и нейросетевых технологий привело к появлению нейронечетких сетей ANFIS.

Результаты сравнительного анализа моделирования работы турбины двигателя (см. Рисунок 3) в библиотеках Python по машинному обучению (Scikit-learn, Tensorflow, Keras, pyTorch) показал, что в них реализован функционал по работе с нейронными сетями прямого распространения, но отсутствует реализация функций для моделирования нейронечетких сетей ANFIS, что было исправлено.

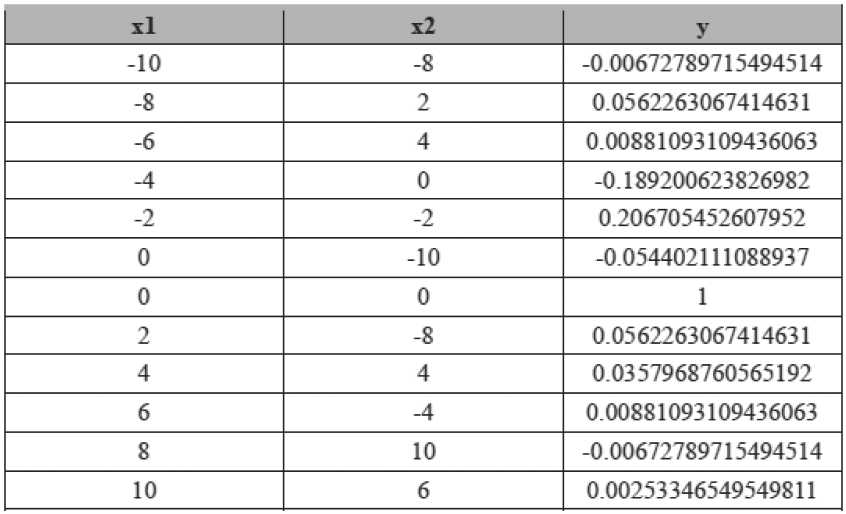
Рисунок 3. Обучающая выборка

Таким образом, сеть будет иметь на входе две переменные – x 1 и x 2. Пусть каждая из переменных принимает значение из множества термов {A1, A2} и {B1, B2} соответственно. В таком случае третий слой будет содержать 4 правила. Функция принадлежности A 1 имеет параметры b = –10 и c = 4; A 2: b = 10 и c = 6; B 1: b = –10 и c = 8; B 2: b = 7 и c = 6.

В этом случае имеем следующие функции принадлежности:

ц A 1( x ) = e - ( x + 10) 2 /32; ц A 2( x ) = e - ( x - 10) 2 /72;

ц B 1( x ) = e - ( x +10) 2 /128; ц B 2( x ) = e - ( x - 7)²/72.                    (6)

Данные функции принадлежности представлены на Рисунке 4.

Вычислим выходные значения первого слоя для первого примера обучающей выборки x 1 = -10, x 2 = -8:

µ A 1( x 1) = 1;

µ A 2( x 1) = 0,003866;

µ B 1( x 2) = 0,969233;

µ B 2( x 2) = 0,043938.

Вычислим выходные значения второго слоя:

u 1 = µ A 1( x 1)∙ µ B 1( x 2) = 1 ∙ 0,969233 = 0,969233;

u 2 = µ A 2( x 1)∙ µ B 2( x 2) = 0,003866 ∙ 0,043938 = 0,00017.

Большое практическое использование функции принадлежности слоя фаззификации раскрывается через обратную операцию дефаззификации – процесса перехода от функции принадлежности выходной лингвистической переменной к ее четкому (числовому)

значению. Цель дефаззификации состоит в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить количественные значения для каждой выходной переменной, которые используются внешними по отношению к системе нечеткого вывода устройствами (исполнительными механизмами интеллектуальной системы алгебраических уравнений).

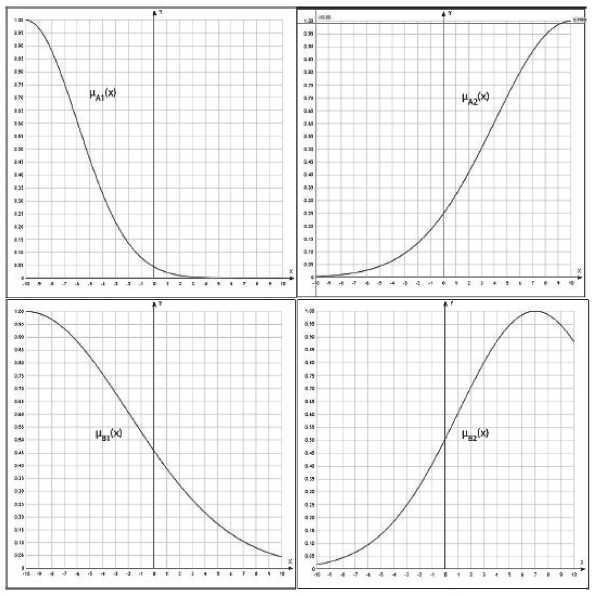
Рисунок 4. Функции принадлежности слоя фаззификации турбины двигателя беспилотного транспортного средства (практический компонент моделирования)

Практико-ориентированная составляющая заключается в возможности редуцирования функции принятия решений, основанной на математическом аппарате сети ANFIS и использовании скалярного компаратора при принятии решений в последовательном изменении состояния гидравлических и механических приводов, клапанов и симплексных (подверженных влиянию со стороны управляющего механизма) устройств. Исследуемый принцип Такаги – Сугено в программной модифицированной реализации имел следующее применение.

Нейросетевая конструкция имеет две входные переменные: ошибка, представляющая собой рассогласование между требуемой и фактической частотой вращения силовой турбины в двигателе беспилотного автомобиля, и скорость изменения ошибки. Терм-множество лингвистических входных переменных содержит по два терма с гауссовыми функциями принадлежности. База знаний содержит четыре предиктивных правила для изменения степени интенсивности работы актуатора турбины в рамках концепции управляемого индустриального интернета вещей.

Заключение и выводы

Проделано моделирование одной итерации процесса обучения для первых двух слоев данной нейронечеткой сети. На каждом последующем шаге выполняются аналогичные

Нейронечеткие системы в моделировании устройств беспилотных транспортных средств

вычисления, в результате которых постепенно изменяются функции принадлежности. Процесс обучения продолжается до тех пор, пока ошибка выхода сети превышает заранее установленное значение. Рассмотрен математический аппарат сети ANFIS.

В рамках данного исследования на программном языке Python реализован класс, позволяющий моделировать работу, обучение и тестирование сети ANFIS, результаты которых были репрезентированы в форме графиков µA1 (см. Рисунок 4).