Нейронная сеть с множественной рекуррентной структурой

В технических приложениях часто возникает задача определения характеристик динамического объекта по результатам измерения его выходных параметров, косвенно связанных с параметрами, характеризующими текущее состояние динамического объекта. К задачам такого типа относятся следующие: косвенное измерение тяги газотурбинного двигателя по ряду его параметров, доступных для измерения; измерение параметров состояния аэродинамических элементов самолета по результатам измерения параметров гидросистемы и другие задачи, решаемые в системах технического диагностирования [1, 2]. Аналогичную задачу решает медико-техническая система для неинвазивного измерения содержания глюкозы в крови человека по данным измерения параметров кожно-мышечной проводимости [3].

Моделью объекта измерения в этих случаях является нелинейная динамическая система, представленная в терминах пространства состояний. Задача измерения, как правило, характеризуется отсутствием необходимых датчиков для измерения полного набора параметров, характеризующих состояние объекта измерения, или невозможностью использовать достаточное множество датчиков в измерительной системе, если она предназначена для использования в целях диагностики. Поэтому в процессе измерения целесообразно выполнять моделирование измеряемого объекта как нелинейной динамической системы, имеющей в общем случае сложные взаимосвязи между параметрами. Для выполнения моделирования в процессе измерения лучше всего подходят искусственные нейронные сети (ИНС).

ИНС имеют способность к обучению, адаптации и дают возможность использовать большое разнообразие нелинейных элементов. Поэтому ИНС используют в информационно-измерительных и управляющих системах для решения задач измерения и управления сложными нелинейными объектами, в том числе с неизвестной структурой. В этих областях другие методы не дают удовлетворительного результата [5–9]. Применяемые для решения задачи измерения ИНС можно классифицировать, как временные сети с линией задержек на входе и с распространением сигнала вперед и динамические (рекуррентные) сети.

Рекуррентные нейронные сети (РНС) включают динамические элементы в форме обратных связей, которые обеспечивают их способность мощного динамического отображения. РНС обладает способностью обучаться динамике системы без знания ее структуры (без знания числа задержанных входов и выходов). Она может реализовать многошаговое предсказание вперед, т. е. модели прогнозирования, которые требуются в приложениях по управлению некоторыми процессами [10]. Достаточно хорошо изучены такие разновидности РНС, как ИНС Хопфилда, Элмана, Джордана [4], полностью рекуррентная ИНС [11], локально ре- куррентная РНС [12, 13], нейроны с памятью [14], РНС с радиальными базисными функциями [15], РНС с блочной структурой [16]. Наиболее близка к анализируемой ниже РНС с множественными обратными связями работа ИНС, предложенная в работе [16].1)

В статье представлены архитектура и процедуры обучения рекуррентной ИНС с множественными обратными связями (РНС_МОС). Основное отличие структуры этой ИНС с множественными обратными связями от других РНС состоит в том, что динамические свойства сети представлены слоями обратной связи (ОС). Сигналы ОС обрабатываются в трех слоях, которые содержат нелинейные активационные функции. В слоях ОС задержанные и соответствующим образом взвешенные выходы скрытого и выходного слоев передаются через активационные функции на нейроны с прямым распространением сигнала. Использование такой структуры расширяет способность ИНС представлять процессы в динамических системах.

В процедуре обучения ИНС (в том числе обучения в реальном времени (РВ)) используется алгоритм обратного распространения во времени (А_ОРВ) [17]. Для того чтобы использовать подобную процедуру обучения, построена "присоединенная" модель РНС_МОС. Модель служит для вычисления производных по весам ИНС, которые используются для цели обучения. Поскольку обучение не в РВ не обеспечивает достаточной адаптации ИНС к изменениям ДС, анализируется вывод процедуры обучения в РВ. В этой процедуре подстройка весов ИНС выполняется по определенному массиву данных вход-выход, хранящемуся в стеке. На каждом временнóм шаге стек сбрасывает наиболее старый элемент и принимает новый элемент от ДС. Поэтому стек содержит достаточно данных, чтобы представлять поведение ДС, и освобождается от слишком старых данных, адаптируясь к изменениям динамики системы на каждом временнóм шаге. Производные для весов РНС_МОС вычисляются по типу усеченного А_ОРВ таким способом, который дает такой же результат, как и развертка во времени через стек. Для настройки весов РНС_МОС используется метод Левенберга—Маркварта с доверительной областью. Функционирование ИНС при обучении, адаптации и обобщении проверены на нескольких прикладных задачах, включая предсказание хаотических временных рядов и идентификацию нелинейной ДС.

РЕКУРРЕНТНАЯ НЕЙРОННАЯ СЕТЬ С МНОЖЕСТВЕННЫМИ ОБРАТНЫМИ СВЯЗЯМИ

Структура

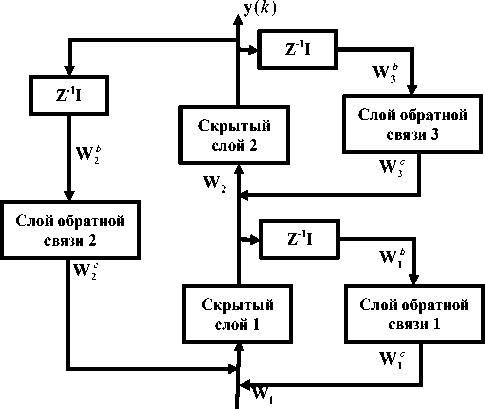
Архитектура РНС_МОС показана на рис. 1, где х ( k ) и у ( k ) представляют вход и выход ИНС, а k — временнóй индекс. ИНС имеет по три слоя с прямым распространением (ПР) и обратным распространением (ОР) сигнала соответственно. В слое с прямым распространением W 1 и W 2 представляют веса между входом и скрытым слоем и скрытым слоем и выходным слоем соответственно. Дополнительно к слоям ПР РНС_МОС имеет два локальных и один глобальный слои ОР. В этих слоях ОР взвешенные суммы задержанных выходов скрытого и выходного слоев поступают на определенные активационные функции нейронов слоя ПР. W ₁ ^c , W ₂ ^c и W ₃ ^c представляют веса связи, связанные с входами нейронов слоя ОР, а z^–1 представляет оператор временнóй задержки. Выходы нейронов слоя ОР ( h ^c ( k ), y ^c ( k ) и z ^c ( k ) ) приложены к нейронам скрытого и выходного слоев через подстраиваемые веса ( W ₁ ^c , W ₂ ^c и W ₃ ^c ) . (Связи смещения ( В ) на нейроны не показаны на рис. 1 для простоты представления структуры ИНС).

x ( k )

Рис. 1. Нейронная сеть с множественной рекуррентной структурой

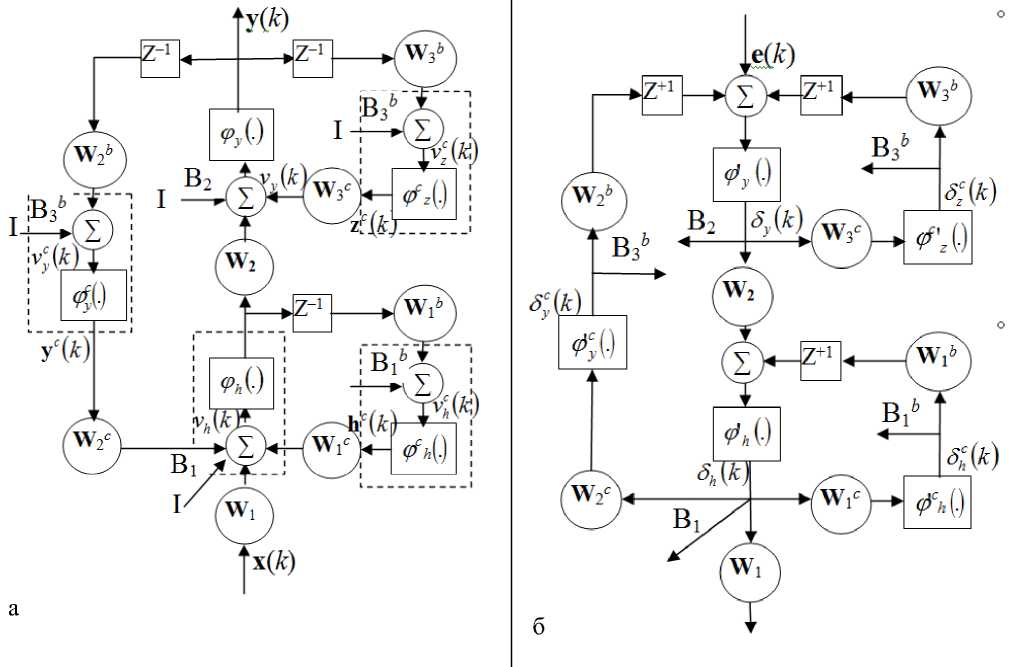
Рис. 2. Обучение РНС_МОС.

a — двухслойная сеть, б — присоединенная модель двухслойной сети

Обучение РНС_МОС

Для обучения рекуррентной ИНС методом, подобным А_ОРВ, требуется вычисление производных. Однако вычисление производных с использованием правила цепочки или разворачивания структуры ИНС по времени достаточно сложно. Поэтому оказывается целесообразным построение присоединенной модели РНС_МОС (рис.2, б), использование которой значительно облегчает вычисление производных. Модель сконструирована путем обращения направления ветвей ИНС, заменой суммирующих сопряжений точками ветвления и заменой операторов временнóй задержки (Z^–1) на операторы упреждения (Z⁺¹). Поскольку веса обновляются методом Левенберга—Маркварта, требуется вычисление якобиана. С помощью присоединенной модели (ПМ) якобиан (матрица Якоби) для выходов РНС_МОС вычисляется путем подачи 1 (в ПМ) вместо соответствующей величины ошибки e и подачи нуля — для других выходов ПМ.

Поэтому после завершения прямой фазы вычислений обратная фаза вычислений выполняется с помощью присоединенной модели РНС_МОС при временнóй последовательности от k = Т до k = 1. Причем, когда прямая и обратная фазы вычисления завершены, чувствительности для каждого веса, которые образуют якобиан, получаются, как в обычном А_ОРВ.

Таким образом, как отмечено выше, элементы матрицы якобиана вычисляются в два этапа, которые условно названы соответственно прямой и обратной фазой. На прямой фазе вычисляются действия РНС_МОС, и они сохраняются вдоль траектории от k = 1 до k = Т . Величина вектора ошибки на каждом шаге k определяется, как разность желаемого и фактического выходов ИНС. Начальные величины для выхода скрытого слоя ( h ) и выходного слоя ( y ) устанавливаются в 0 : h (0) = 0 ; y (0) = 0 .

Образуемые локальные напряжения v(k), производимые на входе активационных функций нейронов обратной связи, определяются выражениями vh (k) = [Wh(k -1)] + B, vy (k) = [W»y(k -1)] + B2,

V 2 (k) = [W? y( k -1)] + B?, где W1b ,W2b ,W3b — входные веса слоев ОР; B1b , Bb2 , B3b — смещения нейронов слоя ОР. При этом выходы нейронов слоя ОР (hc, yc zc) определяются соотношениями hc (k)=ф^ (vch (k)), yc(k) = ф; (vу(k)),      (1)

z c(k)=ф; (v c(k)), где ϕhc , ϕyc , ϕzc представляют активационные функции нейронов слоя ОР. Сетевые величины (vh) для нейронов скрытого слоя и их выходы (h) вычисляются по соотношениям должны быть вычислены веса в присоединенной модели.

После завершения прямой фазы вычислений v , выполняются вычисления для обратной фазы вычисления, которые реализуются на основе присоединенной модели РНС_МОС и проводятся, начиная от k = Т и продолжая до k = 1. Локальные чувствительности при k = Т + 1 устанавливаются в 0:

8 c ( t + 1) = 0, 8 2 ( t + 1) = 0, 8 c ( T + 1) = 0.

Производные активационных функций каждого слоя относительно их входных СВ вычисляются с использованием следующих выражений:

v h ( k ) = №( k )] + [ W c h c ( k )] + [ W c y c ( k )] + B , , (2) ^{h ( k} ) = Ф ь ⁽ v h ^{( k )).}

В соотношениях (2) (и на рис. 2) использованы дополнительные обозначения: W ₁ — матрица весов, передающая v от нейронов входного слоя к нейронам скрытого слоя; B 1 — смещения для нейронов в скрытом слое; W ₁ ^c и W ₂ ^c — выходные веса слоев обратной связи; ϕ_h — активационные функции нейронов скрытого слоя.

Аналогичным образом сетевые величины ( v y ) нейронов выходного слоя и выходы ( y ) этих нейронов определяются соотношениями

Ф С / ^{( v} c ^{( k})) =

5 ф ; ⁽ v ⁽ k )) d v ( k )

ф У / ⁽ v у ⁽ k)) =

,

v = v z ( k )

д ф y (v( k ))

ф.. / (v h(k)) = фУ (v у(k)) =

d v ( k ) дФС к ( v ( k ))	, v = v у ( k )
d Cv ( k )	, v = v h ( k )
д Ф у ( v ( k ))	(4)
d v ( k )	, v = v у ( k )

vy (k) = [W2h( k)] + [Wc zc (k)] + B2, y(k) = Фу (vу (k)X где W2, B2 и φy представляют веса между скрытым и выходным слоями (W2); смещения, приложенные к нейронам выходного слоя (B2); и активационные функции выходного слоя (φy). W3c представляет матрицу весов выхода слоя обратной связи. Сигнал ошибки (е) определен как разность выхода РНС_МОС (у) и желаемого выхода (yd), т. е. выполняется соотношение e(k) = (y(k) – yd(k)). Поэтому при определении мгновенной величины энергии сигнала ошибки в виде выражения E(k) = (1/2)(eT(k).e(k)) функция стоимости, которая служит мерой уровня текущего функционирования ИНС, имеет вид

T

E ..= T Z E ( k )•

T k = 1

Веса ИНС настраиваются так, чтобы минимизировать функцию стоимости (ФС). Поэтому необходимо предварительно определить чувствительность ФС относительно изменения каждого из весов. На k -м временнóм шаге (при любом k ) чувствительность для каждого веса вычисляется путем умножения входа этого веса в РНС_МОС на него же в присоединенной модели. Так что

Ф' . ( v h ( k )) =5^

Использование соотношений (4) позволяет получить локальные чувствительности РНС_МОС:

8 2⁽ k ) = ^[ ф У ⁽ v y ⁽ k ^))] X

x[ e ( k ) + ( ( W b )^T 8 2 ( k + 1) ) + ( ( W b )^T 8 c ( k + 1) ) ] ,

⁸ i⁽ k ) = [ Ф ^ ^{( v} _h ⁽ k ^{))] x}

x[ ( ( W b )^T 8 c ( k + 1) ) + ( ( W b )^T 8 2 ( k ) ) ] ,

8 c ( k ) = [ ф ; / ( v C ( k ))] • [( W c )^T 8 ₂ ( k )],

8 2 ( k ) = [ ф у / ( v у ( k ))] • [( W c )^T 8 1 ( k )], 8 c ( k ) = ^_h- ( v h ( k )) ]•[ ( W c )^T 8 1 ( k ) ].

В случае вычисления матрицы Якоби (так называемого якобиана) вектор e ( k ) в первом выражении в (5) полагается равным единичному, т. е. e ( k ) = 1 . Тогда чувствительность для каждого веса вычисляется путем умножения величин, масштабированных этим весом в РНС_МОС и присоединенной модели, с использованием выражений:

д® = 8 2 ( к ) h T( к ), д W 2	д ет = 6 2( * ), д В 2
д е к = 8, ( к ) х т( к ),	д е к = 8, ( к ),
д W 1     1	д В ,       1
д е к = 82 ( к ) z c т( к ),	д е ( к ) = 8 c ( к ) у т( к - ,),
д W 3 c    2	5 W 3 b    3
д ек = 8, ( к ) у c т( к ),	д е ( к ) = 8 c (к ) у т( к - ,),    (6)
д ^ с    1	5 W 2 b    2
д е к = 8, ( к ) h c т( к ),	д е ( к ) = 8 c ( к ) h т( к - ,),
д W 1 с    1	5 W , b     1
деё к 1=8 з (к )■ д В з	д ев к 1=8 c ( к ), д В 2
к 1 = 8 С ( к ). д В,

Общая чувствительность для каждого веса ИНС получается суммированием относительных чувствительностей в (6) по соответствующей временнóй траектории. (Т. е. для разных временн ы х моментов: при ПР от к = 1 до к = Т + 1, а при ОР от k = Т + 1 до k = 1). Якобиан J , который требуется для обучения РНС_МОС, выражается соотношением (7).

J =

" д е

д е

д е

д е

д е

д е

д е

д е

д е

д е

д е

д е

д е "

.            (7)

[d W 1

д В 1

д W 1 c

д ^ 6

д В b

д W 2

д В 2

д W 2 c

д W 2 6

д В 2

д W 3 c

д W: b

д В b J

Вектор градиента g получается из якобиана ( J ) в соответствии с выражением g = J ^T e . Вектор веса w нейронной сети выражается в виде соотношения

W = [ W в ., w c , W b , в ? ,

W 2 , B 2 , W 2 ^c , W 2 ^b , B ^b 2 , W 3 ^c , W 3 ^b , B 3 ^b ].

Изменение вектора веса на n -й итерации A w n определяется по методу оптимизации Левен-берга—Маркварта

(JTJп + ЦпI)Aw п = - JTen , где цп > 0 — скаляр, а I — единичная матрица. Для достаточно большой величины µn матрица (JTJп + цпI) — положительно определенная и Awп является направлением спуска. Когда цп = 0, Awп является вектором Гаусса—Ньютона. Когда цп ^ да, слагаемое цпI доминирует, так что Awп ^- ц-JTеп представляет чрезвычайно малый шаг в направлении крутого спуска. Для определения μ может быть использован метод Флетчера с доверительной областью [Химмельблау].

Структура алгоритма обучения в реальном времени (РВ)

Процедура обучения РНС_МОС в РВ предусматривает сохранение обучающих образцов за небольшой интервал времени, которые помещаются в так называемом стеке2) определенного размера (L). На каждом временнóм шаге стек покидает самый старый образец и в то же время стек принимает новый обучающий образец от ДС. Поэтому стек должен иметь подходящий размер, чтобы содержать достаточно данных, представляющих динамику системы, и освобождаться от слишком старых данных, адаптируясь к изменениям динамики системы на каждом временнóм шаге. Чувствительность весов РНС_МОС вычисляется методом развертывания ИНС во времени посредством стека. Обучение в РВ выполняется с использованием всех образцов, хранимых в стеке на каждом временнóм шаге, методом Левенберга— Маркварта с доверительной областью.

Обучение РНС_МОС выполняется подстройкой вектора весов w на каждом временнóм шаге w k +1 = w k + Δ w k . Функция стоимости на каждом временнóм шаге определена соотношением

1 L — 1

E = vrE { ^[ y ^{( к} - m ) ^- y p ^{( к} - m ^{)] т х}

² L m = 0

х[у(к - m) - yp (к - m)]}, где L — размер стека, который определяет длину используемых данных, а m — индекс временнóй задержки. yp и y представляют желаемый выход ДС и выход РНС_МОС соответственно. На каждом временнóм шаге обучение выполняется по L образцам.

Элементы якобиана вычисляются в два этапа, которые условно называют прямой и обратной фазами. Прямая фаза вычислений выполняется на ( L – 1) шагов обратно во времени до текущего времени (от k – L + 1 до k ), и величины ( x , h , y , h c , y c , z c ) сохраняются на каждом шаге. Величины ошибок, которые получаются как разность между выходом анализируемой системы (сохраняемым в стеке) и выходом РНС_МОС, также сохраняются. После завершения вычислительной фазы "вперед" выполняется обратная фаза вычислений с использованием присоединенной модели РНС_МОС. Фаза начинается с текущего момента времени k , двигаясь назад на ( L – 1) шагов до времени k – L + 1. Затем вычисляются элементы матрицы якобиана также в форме прямой и обратной фазы. Эти вычисления соответствуют алгоритму обратного распространения во времени путем разворачивания РНС_МОС во времени через стек. Процедура обучения выполняется в РВ, и динамическое вычисление производных выполняется по более чем одному образцу в стеке, и тем самым мы уходим от недостатка статического вычисления градиента и использования только одного образца в текущий момент времени.

ЗАКЛЮЧЕНИЕ

Рассмотрены структура нейронной сети с множественными обратными связями (НС_МОС) и процедура ее обучения. В отличие от архитектуры используемых в приложениях рекуррентных ИНС особенность структуры анализируемой ИНС_МОС состоит в том, что нейроны обратной связи (ОС) организованы в три отдельных слоя с нелинейными обрабатывающими элементами. При этом реализуются достаточно разнообразные виды обратных связей: (выход ИНС—1-й слой ОС— вход выходного слоя); (выход ИНС—2-й слой ОС—нейроны входного слоя); (входной слой— нейроны 3-го слоя ОС—нейроны входного слоя). Такое усовершенствование принятого подхода к построению рекуррентных ИНС (РНС) создает дополнительные возможности построения адаптивных систем, повышения робастности ИНС при решении задач восстановлении формы сигналов из многоканальной смеси в форме свертки и в других приложениях, связанных с моделированием динамических систем и обратных фильтров. Ценой использования таких преимуществ ИНС_МОС является сложность алгоритма ее обучения. Сравнительно с дифференцированием нейросетевых ве- личин (которое необходимо РНС при обычно используемом алгоритме обучения, называемом алгоритмом обратного распространения во времени) для ИНС_МОС такое дифференцирование усложняется за счет того, что структура ее ОС гораздо сложнее. Значительное уменьшение вычислительной нагрузки при вычислении чувствительности сетевых величин относительно весов сети достигается путем построения для ИНС_МОС ее "присоединенной" модели. Приведена "присоединенная" модель и показаны правила ее использования для вычисления чувствительности сетевых величин в ходе обучения ИНС с настройкой ее весов.

Качество функционирования ИНС подобной структуры при обучении, адаптации и идентификации динамических моделей и ее преимущество перед рекуррентными нейронными сетями более простой архитектуры проанализированы Савра-ном (Savran) на основе решения нескольких прикладных задачах, включая предсказание хаотических временных рядов и идентификацию нелинейной ДС.