Нейронные сети как инструмент совершенствования математической модели движения судна

e-mail: , ORCID:

Пашенцев С. В. Нейронные сети как инструмент совершенствования математической модели движения судна. Вестник МГТУ. 2023. Т. 26, № 4. С. 472–488. DOI: 1560-9278-2023-26-4-472-488.

Pashentsev, S. V. 2023. Neural networks as a tool for improving the mathematical model of ship motion. Vestnik of MSTU, 26(4), pp. 472–488. (In Russ.) DOI:

Нейронные сети, как аппарат искусственного интеллекта, применяются для решения множества прикладных задач¹ ( Bishop, 2006; Hagan et al., 2014; Николенко и др., 2018; Хайкин, 2019; Редько, 2022 ), таких как распознавание сложных образов; классификация; прогнозирование; решение регрессионных задач. Этот аппарат не используется для анализа сложных многокомпонентных математических моделей движения судов. Некоторое подобие такого подхода было рассмотрено в работах ( Пашенцев и др., 2006; Позняков, 2006 ), где обсуждалась проблема влияния вариаций параметров модели на маневренные характеристики, полученные при испытаниях модели. В настоящее время появился и успешно развивается математический аппарат в виде нейронных сетей, который можно использовать для оценки перекрестных влияний параметров модели на маневренные характеристики, генерируемые моделью.

По указанной тематике опубликовано большое количество статей (в том числе в "Вестнике МГТУ") и монографий. Поэтому настоящий материал не нуждается в какой-либо детализации и обсуждении по поводу выбора структуры модели, ее идентификации, модельных испытаний. В настоящей статье рассматривается такая задача для многопараметрической модели движения судна в перемещениях ( Справочник…, 1985 ), которая содержит 16 параметров. Соответствующая нейронная сеть будет содержать 16 входов, а ее выходом будет одна маневренная характеристика модели (среди характеристик выбирается любая, например, диаметр установившейся циркуляции Dc). В дальнейшей работе можно менять архитектуру сети с целью получения наиболее точного прогноза, сохраняя число входов (16) и выходов (1). Технология конструирования полной архитектуры сети, т. е. определения числа скрытых слоев и числа нейронов в каждом из них, зависит от программной среды, в которой осуществляется работа с сетью. В ходе исследования использовались пакеты Statistica Neural Networks. Release 4.0E. StatSoft Inc. и ANN (Artifical Neural Nets) в системе программирования SciLab. Главное в процессе работы с сетью – ее обучение, для чего требуется большой массив входных данных, поэтому важно "добыть" этот массив, используя доступные средства. После идентификации математической модели, т. е. определения ее параметров, проводится стандартное испытание модели на циркуляцию с помощью разработанного нами программного комплекса ( Пашенцев, 2018 ). С этой целью фиксируются исходный (базовый) набор (16 параметров) и полученный диаметр Dc; затем специальной подпрограммой, добавленной в комплекс, генерируются вариации базовых параметров; испытывается варьированная модель, фиксируются полученные величины Dc. Данные наборы отправляются в открытый для записи файл, заканчивается запись для установленного числа вариаций; создается файл входных данных (параметров модели и величин Dc), которые и будут массивом для обучения сети.

Материалы и методы

Процедуру, описанную выше, применим для моделирования движения танкера типа "Саратов" водоизмещением 30 000 тонн и определим параметры его модели в перемещениях в грузу, следуя алгоритмам, указанным в работе ( Юдин и др., 2015 ). Математическая модель движения состоит из трех дифференциальных уравнений первого порядка относительно продольной скорости судна Vx, поперечной скорости Vy и угловой скорости поворота судна ω относительно вертикальной оси. Для выбранного типа судна с учетом его теоретического чертежа определим набор коэффициентов модели, которые отражают гидродинамические воздействия среды на корпус судна. Полученный базовый набор коэффициентов приведен в табл. 1 с необходимой для решения точностью.

Таблица 1. Коэффициенты математической модели танкера "Саратов" в грузу

Table 1. Coefficients of the mathematical model of the loaded tanker Saratov

Cx0	0,05	Сm2	2,531379E-03
Cxz	5,846189Е-02	Сm3	2,286795E-02
Cx1	–5,437997E-02	Сm4	1,835252E-03
Сx2	1,346752E-03	СkmOm	7,593681E-02
CyBe	0,1321832	СkmOm1	0,01215519305
Сy2	0,6389132	СkmOm2	6,604177E-02
Сy3	5,970012E-02	Cyra	2,002089
Сm1	4,810237E-02	Сxra	1,0

Испытания типа "Циркуляция" с этими значениями параметров при начальной скорости 16 узлов и кладкой руля 35 ° дали значение Dc = 246,9 м. Чтобы получить массив данных для обучения будущей сети, варьируем базовый набор параметров с помощью подпрограммы VB6 CreateVarModel() (рис. 1). В подпрограмме случайным образом варьируются все базовые параметры модели с амплитудой варьирования, составляющей 20 % (аа = 20).

Public Sub CreateVarModel()

Randomize Timer

' аа – амплитуда вариаций в процентах

If NumbVariants = 0 Then aa = 0 Else aa = 20

With MyModelVar

.Cx0= MyModel_00.Cx0 * (1 + aa / 100 * (0.5 – Rnd(1)))

' аналогично по всем параметрам модели

End Sub

Рис. 1. Подпрограмма VB6 CreateVarModel

Fig. 1. CreateVarModel VB6 subroutine

С вариантным набором параметров выполняется циркуляция в тех же начальных условиях с фиксацией величины Dc. Каждый набор записывается в файл, откуда затем будут браться данные для обучения сети. Понимая значение числа обучающих данных, для качества обучения формируем массив из 120 наборов, что для первого подхода к регрессионной задаче достаточно. Каждый набор содержит 17 значений (16 параметров модели и выходную величину – диаметр Dc).

На скриншоте главной формы программы испытаний модели ( Пашенцев, 2018 ) (рис. 2) в графическом поле траекторий приведена циркуляция для базовой модели с начальным курсом 60 ° и циркуляции для варьированных моделей с начальным курсом 0 ° (они покрыли некоторую площадь акватории). На отдельной дочерней форме (слева) можно наблюдать список параметров модели и их базовые значения (те же, что указаны в табл. 1). На скриншоте формы также содержится другая информация, которая в данном исследовании не рассматривается.

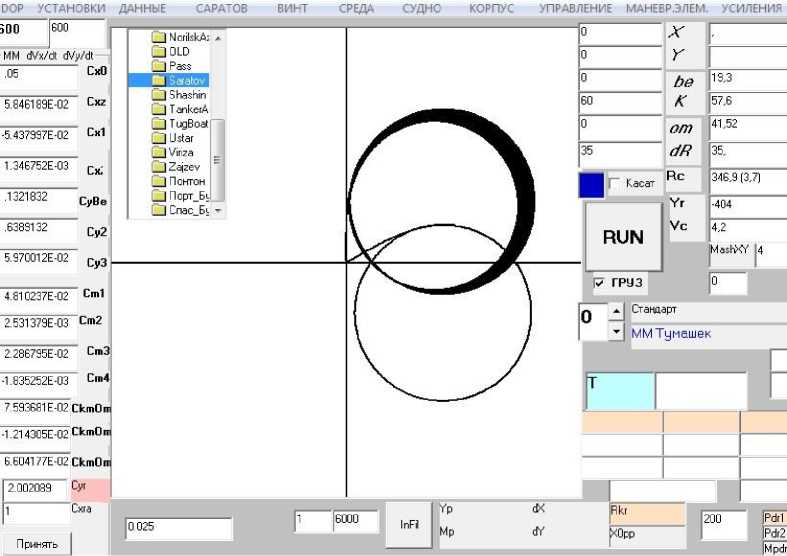
Рис. 2. Результат испытаний моделей с варьированными параметрами по CreateVarModel

Fig. 2. The result of testing models with varied parameters by CreateVarModel

Построение нейронной сети для сформированного набора данных

Получив массив данных для обучения сети, приступим к ее конструированию. Для этого определим конкретные инструменты из большого числа возможностей и выберем два инструмента с учетом удобства пользования ими при сравнении получаемых результатов. Первым используем пакет свободного распространения Statistica Neural Networks. Release 4.0E. StatSoft Inc. (далее – пакет SNN)2. Учтем, что научное сообщество, занимающееся математическим моделированием движения судов, не работает с подобными пакетами; все последующие операции опишем максимально подробно, не считая такой подход излишним. Это позволит специалистам использовать пакет для решения задач моделирования движения судна.

Первоначально таблица с данными бесцветна. После заполнения в верхней части текстовых окон Veriables и Case значениями 16, 1, 70, 30, 20 части таблицы окрашиваются в разные цвета. Это означает, что из 120 наборов данных первые 16 столбцов будут входами (VAR1–VAR16); 17 столбец – выходом (VAR 17, синий цвет); 70 строк данных используются для обучения; 30 строк – для верификации; 20 – для тестирования (на рис. 3 строки окрашены в разные цвета).

^1 g® fii ^ ш]Е1^] ^1^11^1 I I jje] ЫМ1 $1^11

M Dm S«t Edrtcr (TertModelJ20					' 0 i[ e ]Г
				30 ila	-
1И1И®	VAR11	УАЯ12	VAA13	VAA14	VAA15	VAfi16	VAR 17
40	-0.001782	0.08099	-0.01166	0.06603	2.064	0.952	342
41	-0.001775	0.07405	-0.01326	0.0615152	2.011	0.925	347
42	-0.001905	0.077647	-0.01178	0.06849	2.139	0.989	337
«3	-0.001759	0.08328	-0.01266	0.0617	2.068	0.927	342
44 __________ 45	-0.001786 -O.00186E	0.06957 0.08172	-0.01209 -0.01254	0.06697 0.06468	2.002 2.078	0.937 1.064	347 341
46	-0.001757	0.08036	-0.01317	0.068 1 3	2.152	1.001	336	□
47	-0.001784	0.08183	-0.01259	0.06219	2.085	1.011	341
48	-0.001913	0.07794	-0.01106	0.06343	2.134	1.095	337
49	-0.001767	0.07587	-0.01199	0.06237	2.142	1.014	336
50	-0.00176	0.06893	-0.01177	0.07107	2.09	0.987	340
[51	-0.001925	0.07324	-0.01242	0.0691441	1.883	1.07	357
S3	-0.001794	0,08097	-0.01282	0.0614954	1.874	0.939	358
94	-0.001958	0.07009	-0.01104	0.059S7	2.067	1.022	342
96	-0.001813	0.0832	-0.01197	0.07172	2.075	0.941	341
96	-0.001804	0.07649	-0.01164	0.06895	1.864	6.952	359
JZ_______	-0.001969	0.08079	-0.01229	0.06702	2.057	1.035	343
96	-0.001962	0.07385	-0.01207	0.06251	2.005	1.008	347
39	-0.001816	0.07178	-0.013	0.06145	2.013		346
100	-0.001945	0.08305	-0.01147	0.06269	2.062	1.011	342
101	-0.001972	0.0693671	-0.01332	0.06996	1.995	1.021	348
102	-0.001792	0.08178	-0.01213	0.064592	1.939	0.922	352
103	-0.001958	0.07838	-0.01282	0.0684	1.811	0.986	363
104	-0.001812	0.07631	-0.01133	0.06734	1.819	0.905	363
105	-0.001838	0.0703	-0.01313	0.06887	2.074	0.934	342
106	-0.001968	0.07389	-0.01165	0.06264	1.801	0.999	364
107	•0.001788	0.07112	-0.012883	0.07049	2.145	0.9	336
108	-0.001516	0.08007	-0.01236	0.07026	2.158	1.091	335
109	-0.001946	0.0684801	-0.01331	0.06405	1.885	0.956	357
110	-0.001799	0.07411	-0.01176	0.07046	1.815	1.094	363
111 __________	-0.001826	0.0755871	-0.01118	0.06452	2.148	0.904	336 Q.

Рис. 3. Данные для обучения сети с распределенными наборами по характеру использования (черный цвет – обучение; красный – верификация; синий – тестирование) Fig. 3. Data for training network with distributed sets by usage (training – black, verification – red, testing – blue)

Определим архитектуру сети, на которой будут работать эти данные. Для этого сделаем выбор File/New/NetWork, и на мониторе появится дочерняя форма, показанная на рис. 4 (слева), она озаглавлена Create NetWork.

Выберем тип сети – многослойный персептрон (MultiLayer Perseptron), повторяем число входов (16) и число выходов (1), число слоев (No Layers) (4), после чего справа внизу заполняем размеры скрытых слоев сети: Layer 2 = 8, Layer 3 = 3. Эти цифры обозначают числа нейронов в двух скрытых слоях. После выбора Create (создать) получим графическую схему созданной сети (рис. 4, справа). Выполнив эти процедуры, можно перейти непосредственно к обучению сети.

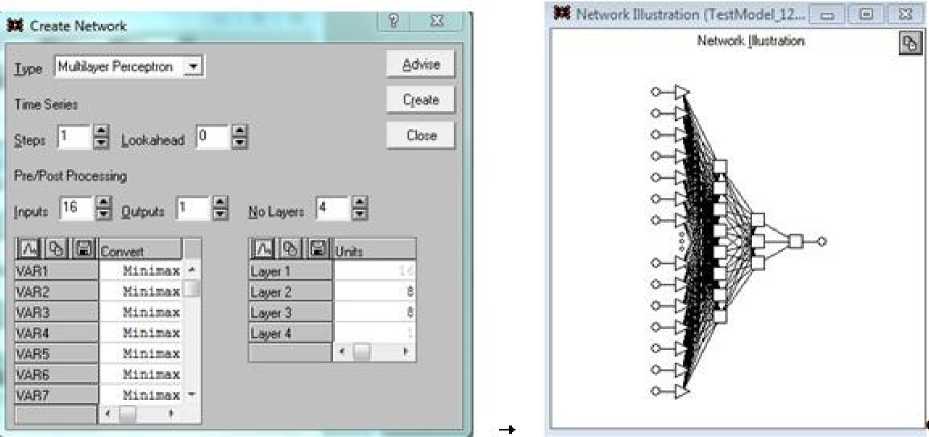
Рис. 4. Процедура создания архитектуры сети (слева) и ее графический вид (справа) Fig. 4. The procedure for creating the network architecture (left) and its graphical view (right)

Обучение сети на сформированном наборе данных

В процессе обучения сети производим выбор по цепочке Train/MultiLayer/Back Propogation. В результате на экране появляется дочерняя форма Back Propogation (рис. 5, справа), которая позволяет выбрать параметры процесса обучения.

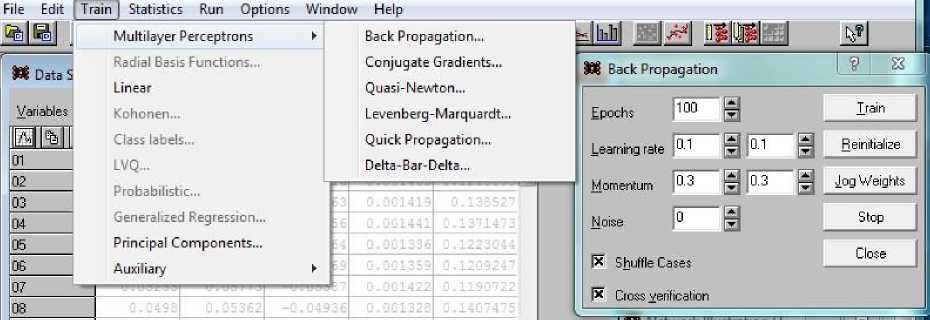
Рис. 5. Включение режима обучения сети и выбора способа совершенствования переходных матриц

Fig. 5. Enabling the network training mode and choosing a way to improve the transition matrices

Числа эпох (циклов) обучения и скорости обучения выберем равными 1000 и 0.01 соответственно. Остальные параметры оставим пока по умолчанию. Важными для результатов обучения являются переключатели (внизу слева) Shuffle Cases (перемешивание наборов) и Cross verification (перекрестное использование обучающих и верификационных наборов). Перемешивание наборов при обучении повышает надежность последующих прогнозов, полученных с помощью обученной таким образом сети. Определив обучающие параметры, нажимаем кнопку Train и запускаем процесс обучения сети ( Bishop, 2006, Николенко и др., 2018 ).

Часть результатов обучения сети представлена на рис. 6. На скриншоте собраны несколько дочерних форм с интересующими нас данными: форма Back Propagation с установленными эпохами и скоростью обучения (слева вверху); архитектура сети (справа); средние квадратические погрешности (СКП) полученного в ходе обучения результата (в средней части): при применении 1–70 наборов TError = 0.38024; 71–100 наборов – VError = 0.7463. В нижней части рис. 6 показано графическое изображение процесса обучения по эпохам в двух цветах: синий – при использовании обучающих наборов, красный – наборов верификации. В текстовых полях (выше графика и справа) приведены значения тех же погрешностей Error T = 0.5245 и V = 0.88587. Эти значения больше, чем показанные выше, так как здесь они соответствуют конкретному прогону, а вышеприведенные значения указывались как среднее между всеми запущенными ранее прогонами обучения.

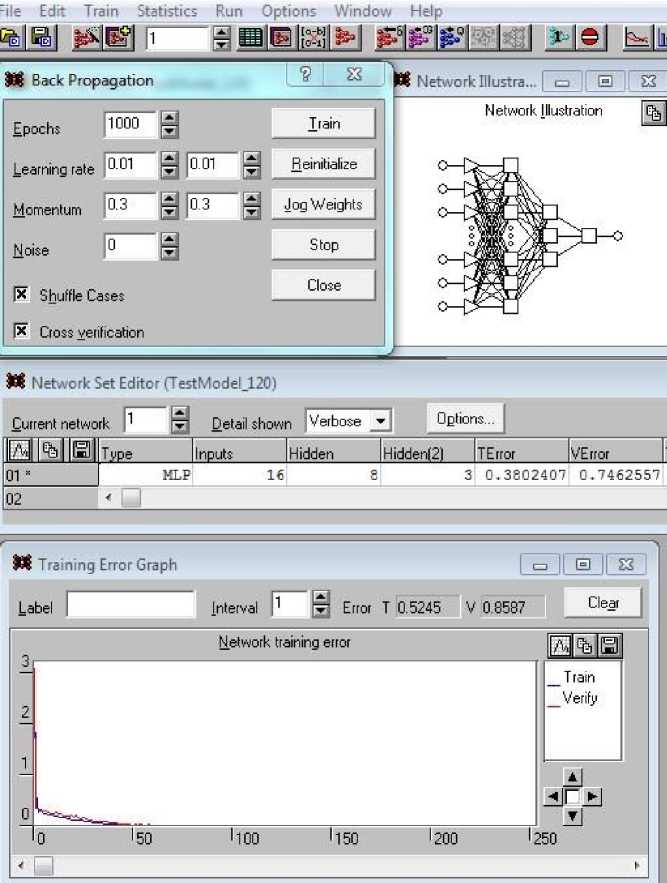
Рис. 6. Часть результатов обучения на трех дочерних формах

Fig. 6. Part of learning outcomes on three child forms

Использование обученной сети для получения выходного результата

Когда сеть обучена, можно использовать ее для решения поставленных задач, таких как задачи регрессии, получения численного результата (прогноза) (задачи классификации, типизации, кластеризации в данном случае не решаются). Для этого сделаем выбор Run/One-off Case; в появившейся на экране форме с тем же названием заполним строку любыми данными, которые необходимо проверить "на результат" (рис. 7). В верхней части скриншота показано появившееся меню, а внизу – форма с линейкой из 16 элементов, которые следует заполнить.

На рис. 7 представлено состояние уже заполненной строки; по ее открытым элементам видно, что указаны значения базового набора данных. Его можно ввести по ячейкам, что займет много времени, поэтому целесообразно сохранить данные в строке Excel, скопировать ее и вставить в строку формы, изображенной на рис. 7 (действие выполнимо, так как форматы данных в Excel и в нашей строке одинаковы). Затем следует нажать кнопку Run и получить в текстовом поле Output результат Dc = 347.35 м, практически совпадающий со значением 346.9, полученным при испытании модели с использованием базового набора ее параметров. Особо отметим, что базовый набор занимал 121-ю строку и не участвовал в обучении сети.

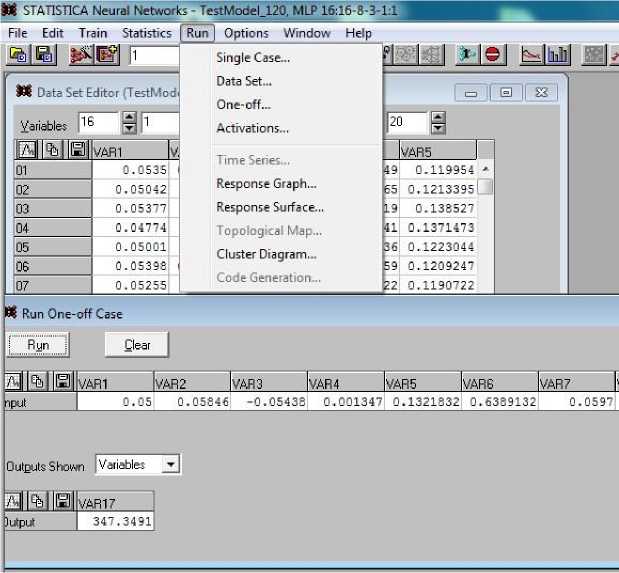
Рис. 7. Проверка работы обученной сети на произвольном наборе входных данных

Fig. 7. Checking the work of the trained network on an arbitrary set of input data

Упрощенный вариант тестирования – использование любой строки из наборов с 101 по 120, так как они специально планировались для целей тестирования. В этом случае в меню (рис. 7) следует выбрать Single Case и в появившейся форме (рис. 8) в текстовом поле Case No ввести номер набора, который хотим проверить. Наберем номер 111, нажмем кнопку Run и получим результат 335.4 (при целевом значении 336). Ниже показана фактическая погрешность порядка –0.6. Нажатие кнопки Up\Down рядом с номером набора меняет его номер на единицу и сразу дает значения Output, Target и Error без нажатия Run.

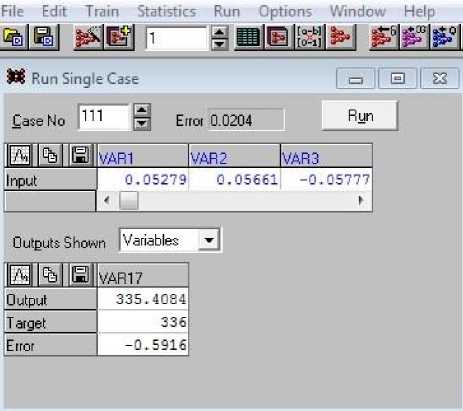
Рис. 8. Проверка работы обученной сети с использованием наборов входных данных 101–120

Fig. 8. Checking the work of the trained network on a set of input data for testing (sets 101–120)

Результаты и обсуждение

На основании вышеизложенного можно сделать вывод, что сеть для поставленной задачи строится без особых усилий и достигаются вполне удовлетворительные результаты по точности прогноза. Результаты целесообразно улучшить посредством вариации действий на различных этапах процесса, но это требует более глубокого погружения в нейросети как самой проблемы, так и конкретной технологии решения. Нейронная сеть фактически вырабатывает матрицы перехода от одного слоя к другому, порядок этих матриц зависит от размера соседних слоев. В нашей сети переход от входа к первому скрытому слою требует создания матрицы размером M(8х16), чтобы при умножении ее справа на вектор-столбец входов V(16x1) получить вектор V(8х1), являющийся вектором входов первого скрытого слоя. Матрица, о которой идет речь, называется весовой. Но реальность несколько сложнее: то, что поступит на вход любого слоя, должно быть обработано нейроном, а не просто пройти через него. Нелинейная функция, которая обрабатывает внутренние входы, называется функцией активации. Данные функции в некотором смысле моделируют работу реальных нейронов; существует набор активационных функций, характеризующихся разной частотой использования. Наиболее часто применяются такие функции, как линейная, сигмоидная, гиперболический тангенс; в некоторых системах программирования можно создавать свои функции активации. В SNN такой возможности нет, поэтому используем тот набор функций, который она предоставляет.

Назначаем функции активации для некоторого слоя выбором Edit\Network, затем в выпадающем списке выбираем нужную функцию (рис. 9). Обратим особое внимание на поле Error function, в котором указана строка Sum-squared, означающая, что система будет использовать для оценки качества обучения сети среднюю квадратическую погрешность, т. е. среднюю сумму квадратов отклонений полученных результатов от целевых значений для данного набора.

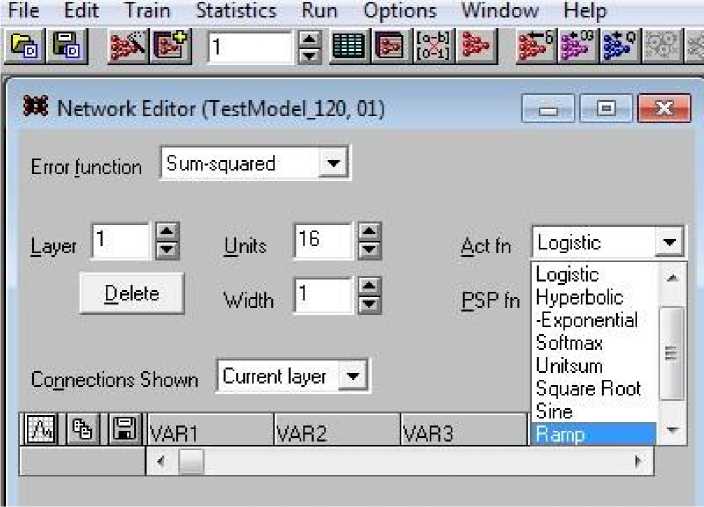
Рис. 9. Выбор функций активации для слоев сети Fig. 9. Selection of activation functions for network layers

В окне Network Editor выбираем номер слоя в поле Layer – входного слоя 1 (число входов 16). Клик на поле Act fn дает выпадающий список с перечнем возможных десяти функций активации: Linear, Logistic, Hyperbolic, Exponential, Softmax, Unitsum, Square Root, Sine, Ramp, Step. Клик на любой функции определяет выбор ее для нейронов всего слоя. Меняя номера слоев и производя такой выбор, определяем все функции активации нашей сети. В дальнейшем их можно менять, исследуя альтернативные архитектуры и следя за эффектом таких изменений по величине СКП.

Строгие установки о том, какие активации следует назначать по слоям, не предусмотрены; скорее, это эвристическая процедура. Целесообразно сделать несколько вариантов сети и выбрать вариант, дающий лучшие результаты (меньшую СКП). Более того, если разрешить системе SNN создавать набор сетей (Set NetWorks) и при изменении сети соглашаться на его сохранение, то все созданные сети остаются в наборе и система сама выбирает лучшую (Best) из них (рис. 10).

В ходе решения конкретной задачи – предсказания диаметра Dc установившейся циркуляции танкера – были проверены сети, имеющие архитектуру 16 → 8 → 3 → 1, при следующих вариантах активационных функций по слоям (табл. 2).

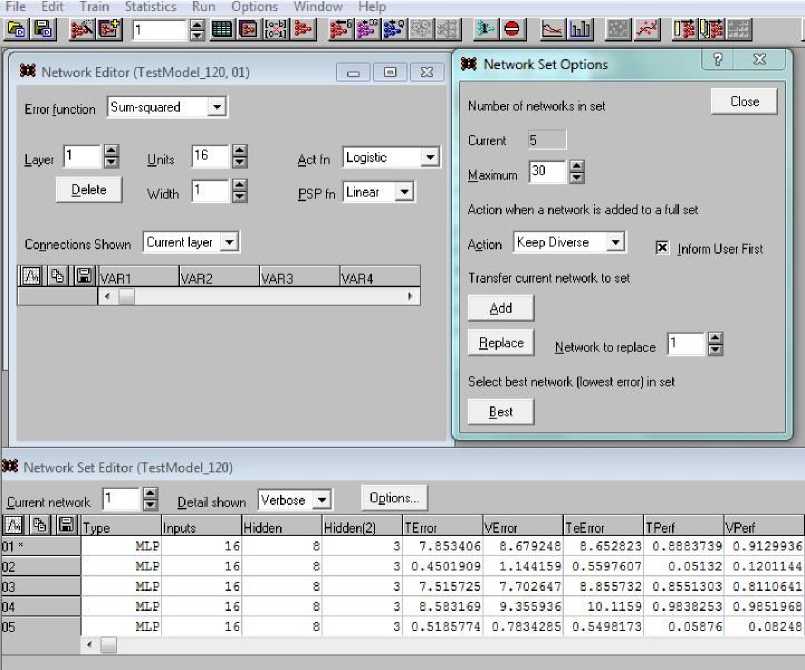
Рис. 10. Создание набора сетей с оценкой точности каждой из них (здесь максимум составляет 30 сетей)

Fig. 10. Creation of a set of networks with an assessment of the accuracy of each (the maximum consists of 30 networks)

Таблица 2. Функции активации по слоям для пяти вариантов сети Table 2. Activation functions by a layer for five network options

Слой 1	Слой 2	Слой 3	Слой 4	TError	VError
Logistic	Hyperbolic	Exponential	Linear	7,853	8,679
Logistic	Hyperbolic	Linear	Linear	0,450	1,144
Logistic	SoftMax	Logistic	Linear	7,516	7,703
Hyperbolic	Logistic	Exponential	Linear	8,583	9,356
Exponential	Hyperbolic	Logistic	Linear	0,519	0,783

Результаты существенно различаются; они приведены в табл. 2 (столбцы под названиями TError и VError). Эти результаты отражают погрешности, полученные по обучающему и верификационному множествам наборов. Система сама выставила иерархию пяти сетей, дав самый высокий уровень пятой сети. Такая полная информация о сетях набора вызвана выбором режима Verbose (подробно) в поле Detail shown.

В форме выше (справа), которая выпадает при нажатии кнопки Options, можно оперировать объектами сетевого набора – отдельными сетями, например, добавить новую сеть (Add) или удалить старую (Replace).

В системе SNN существует еще одна возможность обработки входных и входных данных, которая носит название пред/постпроцессорная обработка. Все установки, связанные с ней, выполняются в форме, которая вызывается выбором Edit/Pre/Post Processing (рис. 11).

Среди процедур предварительной и конечной обработки данных нас интересует процедура, позволяющая понять, как работает система SNN с этими данными. Речь идет о масштабировании данных, которые поступают на вход и должны появиться на выходе. Они крайне неоднородны по значениям (положительные и отрицательные значения; числа порядка сотен и значения порядка 10–3) и тем самым затрудняют работу системы. Поэтому система масштабирует данные так, чтобы все новые нормализованные значения попадали, например, в интервал (0, 1). Для этого используются мультипликативные (Scale) и аддитивные (Shift) коэффициенты, которые указаны в соответствующих столбцах таблицы, представленной на рис. 11.

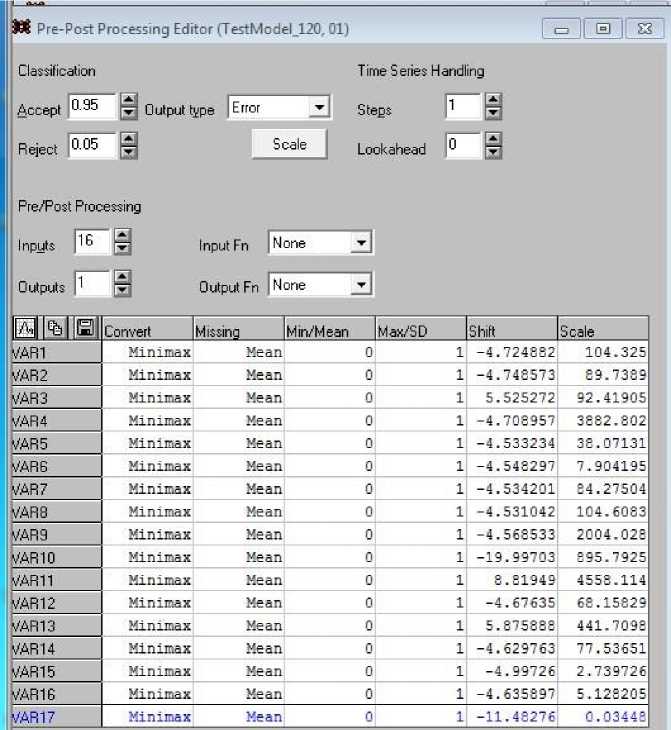
Рис. 11. Пред/постпроцессорная обработка данных

Fig. 11. Pre/post processing of data

Используем это обстоятельство для решения задачи, которая не предусмотрена системой SNN. Сеть обучалась для выходной переменной, в качестве которой был выбран диаметр установившейся циркуляции Dc. Но в равной мере нас интересуют и другие характеристики установившейся циркуляции: скорость хода Vc, угловая скорость поворота omC, угол дрейфа beС (возможен прогноз и других характеристик, но пока ограничимся этими тремя). Для их получения следует трижды сменить выходную переменную, для каждой из них снова провести обучение сети и лишь затем получить требуемый прогноз Vc, omC и beС. Реализуем прогноз иначе: воспользуемся уже существующим прогнозом Dc, который переведем в нормированное значение и с его помощью восстановим прогнозы других переменных в исходном формате (т. е. ненормированном).

В самой системе SNN выполнить указанную задачу невозможно, поэтому прогнозы по Dc для всех 120 наборов данных записываем в виде файла: выбором Run\Data Set получаем выпадающую форму (рис. 12), нажимаем Run и в таблице прогнозных значений для 120 наборов данных выбираем первый столбец обычным обводом. Кликом на выбранной зоне правой кнопкой получаем возможность копирования и затем переноса в блокнот в виде файла. Дальнейшая работа с этими результатами будет происходить в иной вычислительной системе, выберем MathCad15 (далее – MathCad).

В этой среде считываем файл прогнозов Dc и далее работаем с ними; результаты будут показаны на скриншотах из MathCad.

В среде MathCad считываем файл с результатами прогнозов по данным обученной сети с помощью функции чтения READPRN текстового файла TestModel000.txt. Содержимое файла считано в матрицу Mall; в нее включены 121 строка и 20 столбцов, так как к 17 "старым" столбцам мы добавили 3 столбца дополнительных значений маневренных характеристик Vc, omC и beС. Обычными присвоениями получаем четыре вектор-столбца Dc, Vc, omC, beC (рис. 13).

Рис. 12. Выбор прогнозных значений диаметра Dc

Fig. 12. Choice of predictive values of the Dc diameter

namfill .- "C: Users Admin Desktop Mathcadl4 НЕЙРО_СЕТЬ from_SNN_Matr TestModelOOO.txt"

Mall := READPRN(namfill)                    nM := rows (Mall)         nM = 121

De := Mall             omc := Mall         beC > Mall            vc := Mall

Рис. 13. Вектор-столбцы Dc, Vc, omC, beC Fig. 13. Column-vectors Dc, Vc, omC, beC

Затем создаем две пользовательские функции для получения нормированного значения переменной и ее денормированного значения – функции Norm(dc,mi,ma) и deNorm(dcN,mi,ma), в которых mi и ma означают максимальное и минимальное значения некоторого множества. Эти значения для векторов легко найти, используя функции MathCad min() и max(), применив их к векторам Dc, Vc, omC, beC. Приведем их значения для понимания дальнейших действий (табл. 3).

Таблица 3. Минимальные и максимальные значения для четырех маневренных элементов на циркуляции

Table 3. Minimum and maximum values for four maneuverable elements on the circulation

Значение	Dc, м	Vc, м/с	omC, град/мин	beC, град
Min	332	4,137	40,088	18,454
Max	364	4,252	42,783	20,091

Далее из матрицы с данными с целью проверки идеи возьмем произвольно 7-ю строку со значениями этой четверки характеристик 351; 4,205; 41,176 и 19,11. Они были обработаны указанным образом: найдено нормированное значение Dc, названное Ndc = 0,594. С его помощью и функции deNorm определены в MathCad прогнозные значения bec = 19,426; vc = 4,205; omc = 41,689. На скриншоте слева (рис. 14) показаны эти процедуры и полученные прогнозы, правее их приведены действительные значения. Сравнение значений свидетельствует о том, что прогноз стандартных натурных испытаний.

M .    ■    , (de - mi)

Nonn(dcrmi?ma} :=-------- ma - mi весьма удовлетворителен, т. е. адекватен результатам

deNonn(dcN,mi,ma) := mi + dcN ■ (ma - mi)

Ndc := Nonn(351,332,364)

Ndc = 0.594

bee := deNonn(0.594,18.454,20.091)

bee = 19.426

19.11

vc := deNoim(0.594,4.137,4252)

vc= 4205

omc := deNoim(0.594,40.088,42.783)

omc = 41.689

41.176

Рис. 14. Процедуры нормирования и денормирования и полученные прогнозы

Fig. 14. Procedures for normalization and denormalization and the resulting forecasts

Прогнозы носят вероятностный характер, и их совпадение в одной строке не говорит о качестве прогноза в целом. Поэтому ту же процедуру применим к векторам Dc, Vc, omC, beC (рис. 13). С помощью вектора Dc получим нормированный вектор V_Ndc = Norm(V_Dc, 332, 364). Затем, используя только его как основу, найдем денормированные векторы значений остальных характеристик:

V_bedN = deNorm(V_Ndc, 18.454, 20.091);

V_omdN = deNorm(V_Ndc, 40.088, 42.783);

V_vdN = deNorm(V_Ndc, 4.137, 4.252).

Здесь префикс V_ в обозначениях переменных подчеркивает их принадлежность к вектор-столбцам.

Значения этих векторов не приводятся, так как каждый из них содержит 120 элементов (строк).

Вычислим среднюю квадратическую погрешность прогноза для этих характеристик по всему множеству из 120 наборов данных. Результат такого сравнения, выполненного в среде MathCad, показан на рис. 15. Денормированные векторы характеристик вычитаются поэлементно из фактических значений, разности возводятся в квадрат и складываются по всем наборам от 1 до 120. Результат делится на число наборов 120 и извлекается корень квадратный. На рис. 15 приведены выражения из MathCad и полученные значения СКП (справа). Cравнение этих значений свидетельствует о том, что совокупность векторов-прогнозов адекватна результатам стандартных натурных испытаний.

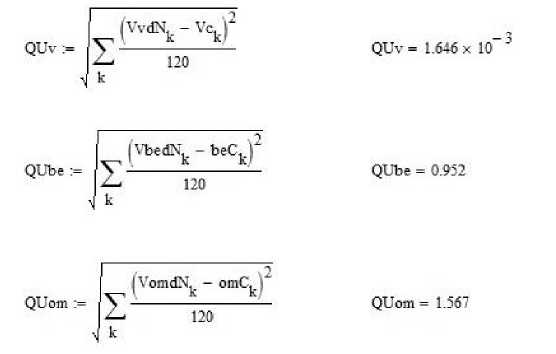
Рис. 15. Расчет средней квадратической погрешности по трем прогнозируемым характеристикам на всем наборе данных Fig. 15. Calculation of the root mean square error for three predictive characteristics on the entire data set

Полученные результаты дают основание заключить, что предлагаемый подход к прогнозу всех характеристик по прогнозу только одной из них оправдывает себя. Действительно, подсчитаем относительные погрешности этих трех прогнозов: делим каждую СКП на среднее значение прогнозируемого параметра:

– для Vc (0,001646 / 4,2)∙100 % = 0,04 %;

– для beC (0,952 / 19,3)∙100 % = 4,9 %;

– для omC (1,567 / 41,5)∙100 % = 3,8 %.

С технической точки зрения, полученные значения свидетельствуют об удовлетворительном результате применения рассматриваемого подхода к прогнозу всех характеристик, т. е. предлагаемый способ можно считать работающим.

В введении было отмечено, что мы воспользуемся двумя вычислительными средствами для решения поставленной задачи. Предыдущие результаты были получены с помощью среды SNN; все этапы решений, анализа и совершенствования результатов продемонстрированы на формах, предоставляемых этой средой (рис. 2–12). Такая работа очень эффективна, если необходимо получить конкретный статичный результат. Но система SNN не дает возможности использовать результат динамично, применяя его немедленно, например, для целей управления. Она также "скрывает" часть промежуточных результатов, не позволяя реализовать их для собственных целей изменения промежуточных результатов.

Поэтому логично использовать среду с языком программирования и расширяющими пакетами, которые содержат функции для работы с нейронными сетями. Нами выбрана среда SciLab³ ( Satish…, 2009 ), свободно распространяемая в Интернете, содержащая язык программирования высокого уровня и набор прикладных пакетов, в том числе пакет ANN (Artifical Neural Nets) для работы с сетями. Он подгружается в вычислительную среду SciLab средствами системы. В разделе help среды SciLab описаны 30 функций пакета ANN_toolbox. Несколько из них приведены в табл. 4 в оригинале и с переводом.

Таблица 4. Функции пакета ANN_toolbox Table 4. Functions of the ANN_toolbox package

Функция	Перевод
ann_FF_INT – internal implementation of feedforward nets	– внутренняя реализация сетей прямого распространения
ann_FF_grad – error gradient trough finite differences	– градиент ошибки через конечные разности
ann_FF_grad_BP – error gradient trough backpropagation	– градиент ошибки через обратное распространение
ann_FF_init – initialize the weight hypermatrix	– инициализировать гиперматрицу весов
ann_FF_run – run patterns trough a feedforward net	– запускать паттерны через сеть прямого распространения
ann_d_log_activ – derivative of logistic activation function	– производная от логистической функции активации
ann_d_sum_of_sqr – derivative of sum-of-squares error	– производная ошибки суммы квадратов
ann_log_activ – logistic activation function	– функция логистической активации
ann_pat_shuffle – shuffles randomly patterns for an ANN	– случайным образом перемешивает шаблоны для ИНС

Часть терминов нам знакома по пакету SNN (например, Backpropagation, Activation function и др.), что облегчает переход в новую программную среду. Используя эти функции, можно решать вариативные сетевые задачи в автоматизированном режиме. К тому же все функции имеют открытый код, что отличает новую среду от системы SNN, где такие решения выполняются только в ручном режиме. На рис. 16 показан короткий отрезок программы SciLab, демонстрирующий применение всего лишь двух функций для обучения сети и получения тестового решения. Строки программы пронумерованы для удобства комментирования.

Прокомментируем программу, в начале которой без номеров приведена написанная нами функция активации, являющаяся несомненным преимуществом программного решения (такой возможности не было в SNN). Функция оформлена определенным образом: ее собственное имя sirelu обрамлено ключевыми словами ann_ и _activ, только тогда она узнается системой. Поэтому следующая за ней функция является производной от sirelu, ее отличает добавление в имя символа дифференциала d. Производная необходима для реализации процедуры BackPropagation оптимизации сети.

Строка 1 открывает текстовый файл для чтения с 120 наборами данных для обучения (он знаком по работе в SNN). В строках 2–4 происходит чтение файла в матрицу с именем ISXODN, после чего файл закрывается строкой 5. В строке 6 заданы значения параметров структуры сети 16, 8, 3, 1. Они вносятся строкой 6 в список NN, он определяет затем архитектуру сети. В строках 9 и 10 содержатся матрица входов L_INPUT и вектор целей L_GOAL из 70 строк для обучения. В строке 11 определен список fa, состоящий из трех строчных значений с именами функций активации по слоям сети.

function [y]= ann_sirelu_activ (x)

y=x/(1+exp(-x))

endfunction function [y]=ann_d_sirelu_activ(x)

y=(1+exp(-x)*(1+x))/((1+exp(-x))*(1+exp(-x))) endfunction

• 1.    f=mopen('c:\dats\TestModel_120.txt','r');

• 2.    for i=1:120; for j=1:17;

• 3.    ISXODN(i,j)=mfscanf(f,'%g');

• 4.    end; end;

• 5.    mclose(f);

• 6.    nS0=16;nS1=8;nS2=3;nS3=1;

• 7.    NN=[nS0 nS1 nS2 nS3];

• 8.    r=[0 1];

• 9.    L_INPUT=ISXODN(1:70,1:nS0);

• 10.    L_GOAL=(ISXODN(1:70,nS0+1));

• 11.    fa=['ann_tansig_activ','ann_logsig_activ','ann_sirelu_activ']

• 12.    W_gd=ann_FFBP_gd(L_INPUT',L_GOAL',NN,fa,0.001,1000,1e-10,1e-10);

• 13.    k=105;

• 14.    goal_test=TEST(k,nS0+1);

• 15.    input_test=TEST(k,1:nS0);

• 16.    y_test_gd=ann_FFBP_run(input_test',W_gd,fa);

Рис. 16. Программа в SciLab, решающая задачу обучения сети и выполнения тестового решения

Fig. 16. Program in SciLab that solves the problem of training the network and executing a test solution

Главной в программном коде, показанном на рис. 16, можно считать строку 12, в которой используется функция ann_FFBP_gd, значение которой присваивается переменной W_gd. Это сложная списочная переменная, которая содержит в качестве элементов три весовые матрицы переходов W между слоями и три вектора смещений S. Они получены в процессе обучения сети, определяют переход от слоя к слою и гарантируют минимально возможную погрешность результатов прогноза. Этот переход можно описать формулой

Vвых = fa(WVвх + S), где Vвх, Vвых – вектор-столбцы входа и выхода; W – матрица весов; S – вектор смещения; fа – функция активации.

Далее можно употреблять элементы W и S в своих целях, например, самостоятельно оценивать погрешность или проверять действие разных функций активации, в том числе и собственного конструирования ( Clevert et al., 2015 ) . Удобно также организовывать работу по прогнозу с новыми наборами данных. Строки 14 и 15 позволяют выбрать для тестирования любую строку k (здесь k=105) из массива данных input_test и соответствующий ей результат goal_test. Тестирование выполнено в строке 16 программы обращением к функции пакета ann_FFBP_run.

Результаты выполнения программы приведены на рис. 17, где показаны процесс обучения сети по эпохам (слева) и график этого процесса в виде MSE (СКП), а также приведен целевой результат 348 и его прогноз 357, выполненный в строке 16. Относительная погрешность составила 9/348 ≈ 2,5 %.

Полученные результаты требуют более глубоких сравнительных оценок, которые предстоит провести в ходе дальнейших исследований по данной теме.

В среде SNN матрицу весов W и вектор смещения S также можно получить; они появляются на форме NetWork Editor (рис. 18). На ней в формате Excel выведены эти важные элементы работы по обучению сети, которые можно перенести в среду Excel, выделив мышкой всю область экрана монитора, и обычным копированием перенести на лист табличного процессора. Затем следует работать с частями этой области обычным образом.

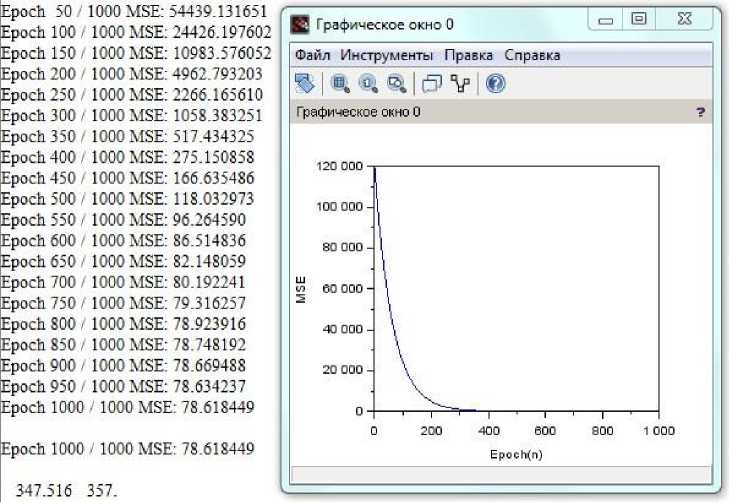
Рис. 17. Результаты выполнения программы

Fig. 17. The results of running the program

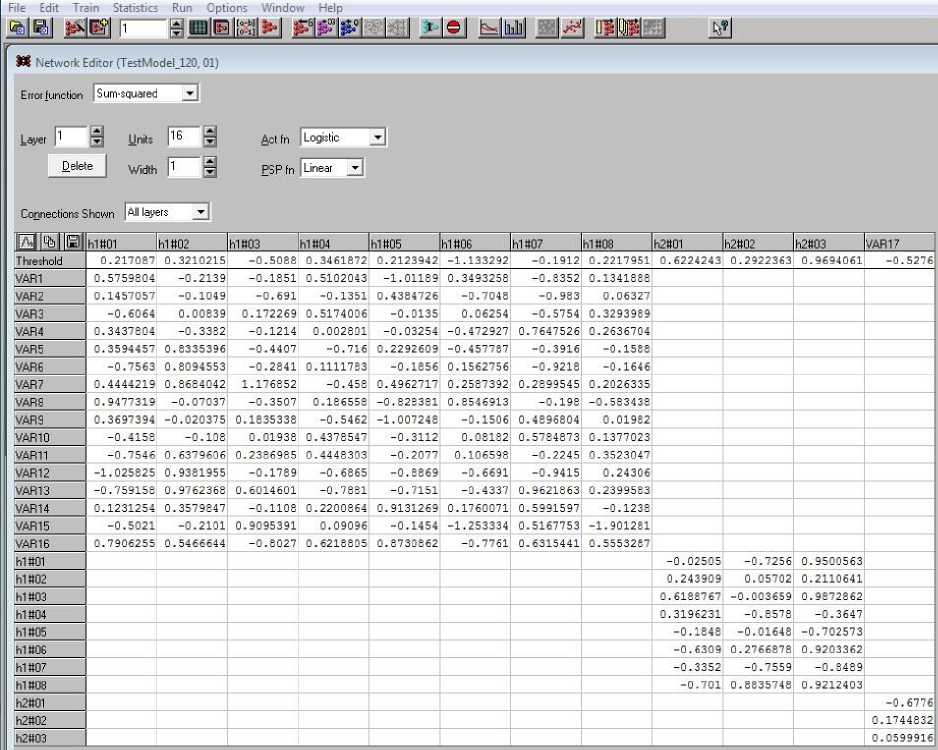
Рис. 18. Весовые матрицы и векторы смещения между слоями сети Fig. 18. Weight matrices and bias vectors between network layers

Диапазон ячеек (рис. 18) обозначим как (h1#01:Treshhold,var17:h2#03). Его первая строка содержит только коэффициенты смещения между слоями: S1 – 8 значений; S2 – 3 значения; S3 – 1 значение. Диапазон ячеек (h1#01:var1, h2#08:var16:) является первой матрицей весов W1, диапазон (h2#01:h1#01, h2#03:h1#08) – второй матрицей W2, диапазон (var17:h2#01, var17:h2#03) – матрицей W3 (столбец).

Пакет ANN в SciLab дает возможность непосредственно (без выполнения дополнительных процедур) обращаться к этим характеристикам. В программе (рис. 17) это делается так: W_gd(1), W_gd(2), W_gd(3), где W_gd – список, полученный в строке 12.

Выводы

Оценка возможностей использования аппарата нейронных сетей для исследования математических моделей движения судна показала, что коррекция с помощью сети идентифицированных параметров выбранной модели адекватна результатам стандартных натурных испытаний, определенных резолюцией ИМО № 137 от 2002 г. "Стандарты маневренных качеств судов".

При использовании программного комплекса ( Пашенцев, 2018 ) появляется возможность: а) проведения произвольного числа испытаний вариативных моделей судна и получения массива данных для работы по обучению нейронной сети; б) построения сети, имеющей в качестве входных данных параметры модели и любую из маневренных характеристик в качестве выхода.

Сеть выбранной архитектуры построена с помощью пакетов StatisticaNN и ANN SciLab, обучена на массиве из 120 наборов данных, результат обучения использован для целей прогнозирования (регрессии). Ошибка не превысила приемлемого технического уровня (5 %).

Для обычных пользователей более удобным в применении является пакет SNN; быстрее получается конечный прогноз, но результаты прогноза возможно использовать только в ручном режиме.

Программирующим пользователям пакет ANN (в SciLab, аналогично в MathLab) позволяет написать достаточно простую программу, используя функции пакета, и применить полученные результаты для разных целей управления процессом расчетов (например, можно динамически менять выходные переменные из набора данных). Эта возможность является преимущество данного пакета, хотя требует дополнительной работы программистов.

Работа с нормированными данными в SNN позволяет по нормированному выходному результату одной из маневренных характеристик (например, Dc) предсказать достаточно точно остальные характеристики (Vc, beC, omC) для установившейся циркуляции, не производя для каждой из них нового обучения сети.

Констатируем в итоге, что с помощью нейронной сети решена поставленная задача определения маневренной характеристики судна по параметрам математической модели. Это решение открывает возможность выполнения главной (обратной) задачи – определения параметров математической модели по заданным маневренным характеристикам судна. Подобные исследования будут выполняться в рамках кафедральной инициативной НИР в 2023–2025 гг.