Нейросетевая система автоматического управления с переменной структурой

Рассмотрена задача синтеза нейросетевой системы автоматического управления (САУ) технологическим процессом с переменной структурой (СПС) при параметрической неопределенности. Методика основана на принципах многомодульности нейронной сети и переменной структуры САУ. Рассмотрена задача исследования и построения системы управления нестационарным промышленным объектом с запаздыванием.

Постановка задачи

Управление сложными технологическими объектами происходит, как правило, в условиях неопределенности, обусловленной невысокой воспроизводимостью протекающих в них технологических процессов [1]. Одним из эффективных подходов к управлению такими объектами является построение робастных или адаптивных систем на основе обучаемых искусственных нейронных сетей (НС) [2-3]. Однако трудность или, точнее, существенный недостаток классического подхода к робастности, как отмечается в работе [3], кроется в его минимаксной природе: максимально допустимая величина неопределенности, при которой сохраняется робастность, определя ется наихудшим сочетанием параметров объек та. Однако при ориентации на наихудшую воз можную неопределенность, реализация которой на практике может быть крайне маловероятной, получаемые границы робастности оказываются неоправданно заниженными. В связи с этим в статье предлагается подход к построению систем управления слабо воспроизводимыми процессами, основанный на применении в системе нескольких нейросетевых моделей (НСМ) объекта управления, каждая из которых на определенных участках протекания процесса наиболее приближена к фактическому состоянию объекта, и соответствующих им нейросетевых регуляторов, предварительно обученных на основе информации о параметрах модели объекта. В данной работе рассмотрены три случая задания параметров нейросетевой модели объекта:

• 1)    параметры модели получены как среднеарифметические в интервалах неопределенности,

в которых могут находиться параметры объекта – нейросетевая модель НСМ1;

• 2)    параметры модели заданы значениями, соответствующими их наихудшему сочетанию – нейросетевая модель НСМ2;

3)параметры модели заданы среднеинтервальными значениями – нейросетевая модель НСМЗ. При этом модели НСМ2 и НСМ3 дают возможность оперирования интервальными значениями параметров объекта, что позволяет говорить о применимости их в условиях параметрической неопределенности.

Таким образом, под многомодульностью в данной работе понимается применение трех НС-моделей объекта управления (модулей) с определенными параметрами и трех НС-регуляторов (модулей), оптимизированных с использованием соответствующей НС-модели объекта. За счет изменения связей в системе реализуется та или иная априори оптимизированная нейросетевая структура «НС-модель и НС-регулятор», которая должна обеспечить высокое качество переходных процессов в условиях параметрической неопределенности.

очную функцию W ( p ) = К _о6 ехр( - тр'у(Т р р² + Т 1 р + 1), параметры которой находятся в известных интервала

К об ^G L ^K об ’ K ^об J , ^{т G} L ^t , ^т J ’ T i ^G L T 1 ,T¹ J ,

T 2 ^g L t 2 ,T 2 J ■ (1)

На основе априорной информации получены варианты нейросетевой модели объекта НСМ1, НСМ2 и НСМ3, соответствующие трем передаточным функциям объекта WM1(p), WM2(p), WM3(p), которые можно применять как на этапах анализа рабостности системы, так и на этапах синтеза регуляторов. Требуется, не проводя переобучение моделей и корректировку регуляторов в ходе протекания процесса, построить НС с переменной структурой, которая обеспечивала бы приемлемое качество управления объектом в условиях переменных задающих воздействий и переменных параметрах объекта, изменяющихся в пределах заданных интервалов (1). Для обоснования робастно-адаптивных свойств системы необходимо проанализировать степень приспособления к неопределенности в системе:

• -    многомодульной с несколькими (в данном случае с тремя) НС-моделями объекта в контуре управления и изменением структуры системы;

• -    одномодульной с одной НС-моделью объекта.

Решение задачи и результаты

Для решения поставленной задачи в нейросетевом базисе использована нейронная сеть, реализующая принцип прогнозирующего управления с моделью. Структура нейронной системы для одного входа и выхода представлена на рис. 1, а для многомодульной системы – на рис. 2.

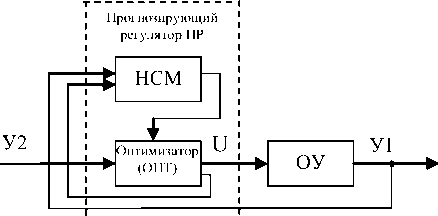
Рис. 1. Схема формирования оптимального прогнозирующего управления: ОУ – объект управления; НСМ – нейросетевая модель ОУ; ОПТ – оптимизатор; ПР – прогнозирующий регулятор

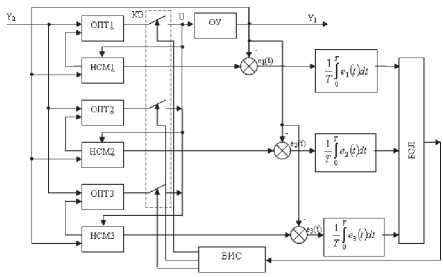
Рис. 2 . Схема САУ с переменной структурой с многомодульной нейросетевой моделью: ОУ – объект управления; БСЛ – блок селектирования сигналов по минимуму; БИС – блок изменения структуры; ОПТ1-ОПТ3 – оптимизаторы; НСМ1-НСМ3 – нейросетевые модели ОУ; КЭ – ключевой элемент

Каждый модуль — это нейросетевой регулятор, включающий НСМ объекта, и оптимизатор (см. рис. 1). Основной принцип прогнозирующего управления состоит в нахождении на каждом шаге дискретности i такой последовательности управляющих воздействий û[i]…û[i+j], которая, будучи приложена к объекту обеспечит макси- мальное совпадение последовательности прогнозируемых значений выхода объекта ŷ [i]… ŷ[i+j] с последовательностью его желаемых значений g[i]…g[i+j]. Эта задача решается путем численной минимизации целевого функционала на за- данном интервале времени, одна из распространенных форм которого имеет вид [4]:

Г            л_г

J = ^|g[i + j]-yi + j]I +

,

El лг          лг1

I u[z + j — 1] — u[z + j — 2] I j=i ^^

где û – управляющий сигнал; g , ŷ – заданная и истинная реакции модели управляемого объекта; N₁ , N₂ – константы, в пределах которых вычисляются ошибка слежения и мощность управляю- ρ – коэффициент, определяющий вклад, вносимый мощностью управления в критерий качества.

Функционал вида (2) регламентирует не только совпадение задаваемых g и прогнозируемых ŷ значений выхода объекта управления, но и соразмерно штрафу ρ накладывает ограничения на интенсивность приращения прогнозируемой последовательности управляющих воздействий û . Существенно, что этот принцип требует наличия динамической модели объекта управления, с помощью которой, собственно, и выполняется прогноз.

Допустим, что имеется несколько квазистаци-онарных режимов работы объекта управления, для которых получены математические модели в виде передаточных функций второго порядка с запаздыванием вида W_мi ( p ) = К_о6 ехр (– τр )/( Т₂²р²+ +Т₁ р + 1); i = 1; 2; 3. Параметры модели объекта в первом случае заданы в виде для i = 1:

N

K об = ∑ K обi /N = 0,1411 [ ⁰ С/м ³ /ч]; i=1 NN

τ = ∑ τ _i /N = 4,02 мин.; T ₁ = ∑ T _1i /N = 25,5 i=1                                                  i=1

N мин.; T2 = ∑T2i /N = 15,28 мин., где N – число i =1

интервалов квазистационарности.

В двух других случаях использована информация об интервальной модели объекта, параметры которой ограничены возможными их значениями в интервалах [ ν_imin, ν_imax ], соответствующих серединам этих интервалов и максимальными отклонениям от них Δ ν_i . С учетом этого параметры модели объекта во втором случае заданы следующим образом:

для i = 2:

К об = 0,383 [ ⁰ С / м ³ /ч]; τ= 6 мин; Т 1 = 14,35 мин; Т ₂ = 25,01 мин;

^{[ к} об ^]=^{[ k} об , ^к об ^] = m ^id v k o6 ^] +4^;

mid [ k ] = ( k + k )/2 = (0,0766 + 0,383)/2 = 0,2298 ;

A = k - k = 0,383 - 0,0766 = 0,3064 ;

[ Т 1 ] = [ Т 1 , Т 1 ] = mid [ T i ] - 1 ;

mid[T 1 ] = (Т 1 + T\ ) / 2 = (14,35 + 41,56)/ 2 = 27,96 ;

5 = Т1 - Т 1 = 41,56 -14,35 = 27,21 ;

[ Т 2 ] = [ Т 2 , Т 2 ] = mid [ T 2 ] + Y ;

mid [ T 2 ] = ( Т 2 + Т 2 ) / 2 = (8,55 + 25,01)/2 = 16,78 ;

Y = Т2 - Т 2 = 25,01 - 8,55 = 16,46 ;

[ t ] = [ t ; t ] = mid [ T ] + ^в ;

mid [T ] = (т + т ) / 2 = (2,2 + 6) / 2 = 4,1 ;

в = T - t = 6 - 2,2 = 3,8, где ki,ki,Т1i,Т1i,Т2i,Т2i,τi,τi – нижняя и верхняя граница коэффициента усиления ki, постоянной времени Т1i, Т2i и запаздывания объекта τi соответственно; mid[νi] – середина интервального параметра [νi].

Параметры модели объекта в третьем случае заданы в виде:

для i = 3

[k o6 ] = ^{[ k} об , ^к об ] = mid ^{[ k} o6 ] =

= ( k + k )/2 = (0,0766 + 0,383)/2 = 0,2298 [ 0 С/м ³ /ч];

[ т ] = [ t ; t ] = mid [ T ] =

= ( t + T )/2 = (2,2 + 6) / 2 = 4,1 мин;

[ Т 1 ] = [ T i T i ] = mid [ T i ] =

= ( Т 1 + Т 1 )/2 = (14,35 + 41,56)/2 = 27,96 мин;

[ Т 2 ] = [ Т 2 , Т 2 ] = mid [ T 2 ] =

= ( Т 2 + Т 2 )/2 = (8,55 + 25,01)/2 = 16,78 мин.

Используя в качестве алгоритма обучения алгоритм Левенберга-Марквардта, проведено обучение НС. Для обучения нейронной сети использовались следующие данные: размер обучающей выборки – 8000; значения входного сигнала – случайные в диапазоне [–6; 6]; максимальная ошибка обучения – 0,00001. Начальное количество нейронов в скрытом слое предварительно принимаем равным трем. Количество циклов (эпох), в течение каждого из которых на вход НС последовательно подаются все элементы обучающей последовательности, а затем вычисляются ее вы- ходные значения и показатели качества обучения, принимаем равным 200.

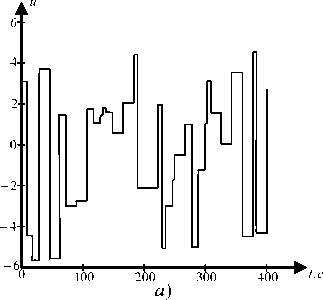
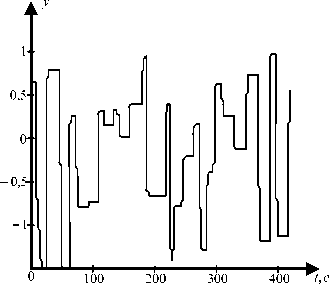
Обучающие данные в виде случайных ступенчатых сигналов подавались на объект и предъявлялись нейронной сети (см. рис. 3). В качестве функции активации скрытого слоя сети выбрана гиперболическая тангенциальная функция, относящаяся к классу сигмоидальных [4]. Функция активации выходного слоя выбрана линейной во всем диапазоне изменения входного аргумента, так как выходы сети могут принимать произвольные значения, если бы в последнем выходном слое сети использовались сигмоидальные функции, то выходные сигналы сети были бы ограничены диапазоном [–1; 1], то есть при поступлении на вход такого слоя сигналов с большими поло- жительными и отрицательными значениями его выход стремился бы к одному из указанных пределов, что нежелательно. Количество нейронов в скрытом слое нейронной сети прогнозирующей модели выбрано равным 9. Обучение нейронной сети было выполнено при N1 = 7, N2= 2, ρ = 0,05 и заканчивалось при достижении ошибки обучения 1,12×10-8, что является показателем успешного проведения этапа идентификации управляемого объекта.

Как видно из рис. 1, каждая нейросетевая модель включена параллельно объекту управления. Сигналы на выходах НСМ и объекта сравниваются. Оценкой приближения переходных процессов на выходах моделей и объекта является

T интегральная модульная ошибка J = 1/T J |e ( t ) dt .

Интервал оценивания Т всегда больше времени переходного процесса Тпп. Сигналы, пропорциональные J1, J2, J3, поступают на блок cелекти-рования сигналов (БСЛ), который настроен на минимум. В БСЛ выделяется сигнал, соответствующий минимальной оценке Ji min , то есть Ji min = min {J1, J2, J3}.

В блоке изменения структуры (БИС) на основе информации о величине Ji формируется командный сигнал, поступающий на переключение ключевого элемента (КЭ). Ключевой элемент в зависимости от выходного сигнала БИС изменяет свое состояние, меняя тем самым структуру системы. Попытаемся теперь за счет сочетания трех структур, отличающихся друг от друга НСМ и величиной управляющего сигнала, минимизирующего критерий качества управления (2), обеспечить апериодические переходные процессы в системе с параметрами объекта, находящимися внутри интервалов неопределенности (1).

е

б)

0,01

0,005

-

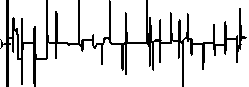
0,005

- 0,01

Для этого проведено численное моделирование нейросетевой САУ СПС (см. рис. 2) при изменении задающего воздействия на четырех I-IV интервалах со следующими параметрами объекта из интервала неопределенности [5]:

• -    I интервал: К об = 0,383 [ ⁰ С / м ³ /ч];

τ = 2,8 мин; Т 1 = 14,35 мин; Т 2 = 8,55 мин;

• -    II интервал: К об = 0,1042 [ ⁰ С / м ³ /ч];

τ = 4 мин; Т 1 = 27,26 мин; Т 2 = 17,3 мин;

• -    III интервал: К об = 0,1042 [ ⁰ С / м ³ /ч];

τ = 4 мин; Т 1 = 41,56 мин; Т 2 = 25,01 мин;

• -    IV интервал: К об = 0,0766 [ ⁰ С / м ³ /ч];

τ = 2,2 мин; Т 1 = 28,16 мин; Т 2 = 16,83 мин.

Результаты моделирования САУ СПС представлены на рис. 4, из которых следует, что на интервалах I и II имеет место структура, определяемая НСМ2, так как min ( J 1 ,J 2 ,J 3 ) = J 2 .

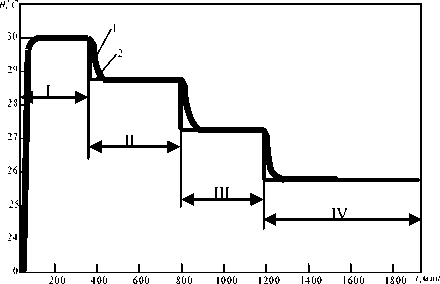
Рис.4.Результаты численного моделирования САУ СПС с нейросетевой моделью объекта управления:

1 – переходный процесс для регулируемой переменной; 2– ступенчатое задающее воздействие; I,II–интервалы работы САУ с моделью НСМ2; III,IV –интервалы работы САУ с НСМ3.Обозначение интервалов I-IV и кривых 1-2 для рис.5 аналогично

⁰         100      200      300      400     ^t,с

в)

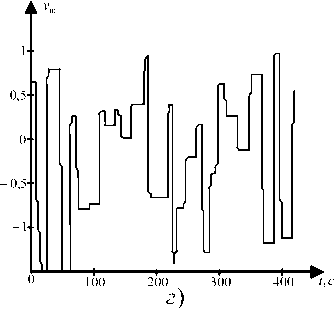
Рис. 3 . Результаты обучения НС-модели объекта: а) сигналы на входах модели и объекта; б) сигналы на выходе объекта; в) ошибка; г) сигналы на выходе НС-модели объекта

В некоторый момент времени при переходе к интервалу IIIструктура системы меняется за счет того, что интегральная оценка J2 становится больше J3, которая продолжает оставаться меньше,чем J1,то есть на третьем интервале min(J1,J2,J3)= J3.Вообще говоря,безразлично,в какой момент интервала IIосу-ществляется смена структуры,однако чем больше к концу интервала [ТII ; Тпп]это произойдет (Тпп – время переходного процесса всегда меньше продолжительности смены задающих воздействий),тем выше вероятность того,что предыдущий переходной процесс закончится и к началу нового изменения задающего воздействия будет включена необходимая структура. В результате исследований установлено,что рассматриваемая САУ на всем интервале функционирования меняет дважды свою структуру:сначала включена структура с НСМ2,а затем – с НСМ3,которые обучены соответственно с моделью при наихудшем соче- тании параметров объекта и при среднеинтервальных значениях параметров.Как видно из рис.4,переход-ные процессы при таком управлении являются апериодическими и эффективно отрабатываются в течение 71,4-114,3 мин.Для сравнения на рис.5 представлены переходные процессы в САУ с одной НСМ.

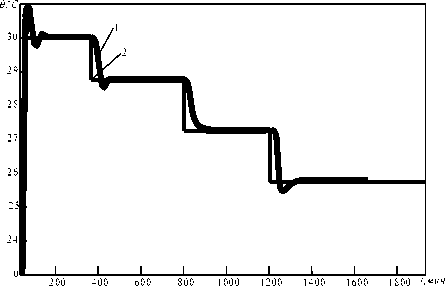
Рис.5 .Результаты численного моделирования САУ с одной нейросетевой моделью объекта НСМ1 на всех интервалах I-IV

Из полученных результатов видно,что реакция системы имеет колебательный характер,а все воздей-ствияотрабатываютсявпределах128,6-157,1мин.,что в 1,4-1,8 раза медленнее,чем в системе с переменной структурой.Следовательно,степень приспособления к неопределенности в многомодульной системе с переменной структурой выше,чем в обычной системе с одной нейросетевой моделью.

Выводы

Из анализа полученных результатов следует,что в САУ СПС обеспечивается повышение эффективности управления,эквивалентного робастному,на основе перестраиваемых в реальном времени предварительно обученных нейросетевых моделей объектов.

Результаты,полученные при исследовании процесса программного управления температурой реактора в системе с многомодульной нейронной сетью,показа-лиследующиепреимуществаСАУСПСпосравнению с обычной системой с одной нейросетевой моделью: 1)возможность наращивания структуры системы за счет подключения новых модулей без переобучения имеющихся в системе; 2) возможность функционирования системы со структурой,оптимальной для каждого состояния; 3)возможность реализации в реальном времени.

Следовательно,многомодульную систему управления целесообразно использовать в сложных задачах робастного и адаптивного управления,где качественные показатели переходных процессов в системе гарантированы затратами времени и памяти вычислительной системы.