Нейросетевая технология идентификации размеров дефекта в полуплоскости на основе временного и позиционного сканирования

Funding information: the research is supported by an internal grant from the Southern Federal University no. ВнГр-07/2020-04-ИМ (RF Ministry of Science and Higher Education)

Введение . Существует обширный перечень различных строительных, мостовых конструкций, зданий, оснований, грунтов, композитных материалов, которые эксплуатируются в различных условиях. Конструкции могут иметь достаточно большой ресурс эксплуатации и дефекты различной конфигурации: трещины, полости, включения, коррозионные изменения структуры, вмятины и пр. Вследствие этого могут возникать непредвиденные предаварийные состояния и отказы конструкции. Для предупреждения аварийного состояния требуется решение задачи их ранней диагностики.

Этот факт определяет необходимость использования различных методов неразрушающего контроля [1– 2]. Некоторые направления развития отдельных методов диагностики наличия дефектов в различных объектах представлены в [3–10].

Основа методов состоит в сборе и анализе определенных параметров конструкции, являющихся откликом при ее нагружении. В качестве одного из таких параметров может быть вибросмещение определенных точек поверхности при импульсном нагружении колебаний конструкции. При этом от места возбуждения колебаний распространяется волновой фронт, возбуждающий смещение точек и колебания всех элементов конструкции. Задача может быть сведена к рассмотрению измерения скоростных параметров распространения волнового поля. Основываясь на анализе публикаций в иностранной литературе, можно констатировать, что экспериментальные исследования показывают явную тенденцию к оперированию методом «измерения скорости» [11–12].

Применение специализированных приборов, которые располагаются в определенных точках объекта и осуществляют сбор информации о различных параметрах колебаний, описаны в [13, 14]. Данная методика предполагает позиционное, временное и частотное сканирование объектов исследования. Наиболее привлекательным является использование акустических датчиков и приемников, установленных на внешней поверхности конструкции. Данные датчики могут фиксировать отраженные сигналы от дефектов. Применение диагностических систем и комплексов требует разработки программного обеспечения (ПО), которое позволяет производить первичный анализ сигнала. В случае «тонкой» приборной настройки, например, при применении специальных алгоритмов обработки по анализу отраженного сигнала, ПО позволяет идентифицировать дефектную область конструкции. Соответствующее ПО может быть разработано на основе использования искусственной нейронной сети (ИНС) [15]. Применение ИНС в задачах реконструкции поврежденного состояния элементов конструкций описано в работах [16–26]. Применение различных архитектур и алгоритмов ИНС описано в [16–20]. Определению дефектов в анизотропных пластинах с помощью ИНС посвящена работа [21]. В работе [22] авторы указали преимущества методов идентификации, не требующих предварительного построения математической модели объекта исследования.

В настоящей работе разрабатывается метод реконструкции диаметра круглого дефекта, расположенного в полуплоскости слоистой конструкции. Такого рода дефекты могут часто встречаться при вскрытии верхних слоев грунтов в виде уплотнений каменных структур под слоями дорожной одежды. Модуль упругости и плотность таких структур могут в разы отличаться от основных параметров слоя. В математической постановке проблема сводится к решению обратной геометрической задачи теории упругости [27]. Рассматривается построение алгоритма восстановления информации об объекте, локализованном в определенном месте. Для этого рассматривается применение метода КЭ , анализ результатов поверхностных волн и корреляционный анализ зависимости параметров дефекта от волнового поля отклика с применением ИНС .

Материалы и методы. Предлагается подход целью которого является восстановление информации о параметрах дефектной области конструкции на основе анализа отклика поверхности среды на ударное воздействие. Анализ осуществляется на основе построенных алгоритмов при сочетании расчетного подхода и применения ИНС . В качестве образца рассмотрен слоистый материал.

Нагружение конструкции импульсным ударным воздействием производится на некотором расстоянии от исследуемой зоны, а датчики, регистрирующие колебания, располагаются в определенных позициях и последовательности в линейном направлении зоны исследования. Могут измеряться поперечные и продольные колебания. Интерес представляет период времени, когда волны, отраженные от концов моделируемого участка конструкции, не успевают достичь датчика. Таким способом имитируется моделирование реальных условий эксплуатации слоистой конструкции грунтового основания. Анализ измеренных амплитудно-временных характеристик ( АВХ ) показывает возможность их использования в обратных задачах восстановления дефектов.

В качестве инструмента решения обратной задачи реконструкции параметров дефекта используется ИНС , которые изначально проектировались для решения задач определения нелинейных зависимостей в многомерных массивах данных. В отличие от других алгоритмов, ИНС не программируются, а обучаются на множестве данных для исследуемых параметров конструкции. Обучающие выборки строятся путем решения прямых задач в конечно-элементном ( КЭ ) пакете ANSYS . Обученная сеть, получив новые, неизвестные ранее результаты анализа, способна корректно распознать параметры дефекта.

Эффективные применения аналитического и численного моделирования, достаточно хорошо коррелирующие с восстанавливаемыми параметрами элементов конструкций, представлены в [28–34].

Постановка задачи. Поставленная задача решается в плоской постановке с помощью метода конечных элементов ( МКЭ ). В настоящей работе используются линейные уравнения теории упругости с учетом диссипации энергии, принятой в пакете ANSYS [34, 35].

Для упругой среды:

• pti- t + xpil _t - а_{м л} — f t ;

° ij ^{— c} ijkl (^£ kl ⁺ P^£ kd ^;

У-кД + Ulkc £kl — 2 , где p — плотность материала; ut — компоненты вектора-функции перемещений; ац — компоненты тензора механических напряжений; ft — компоненты вектора плотности массовых сил; £kl — компоненты тензора деформаций; ci;-kl — компоненты тензора четвертого ранга упругих модулей; x — неотрицательные коэффициенты демпфирования (в ANSYS).

Механика

Рассмотрим подробнее механические краевые условия. При определении механических граничных условий граница тела представляется в виде объединения непересекающихся областей 5 — 5 _u 5 _t 5 _ut , на которых задаются следующие условия:

• —    условие закрепления границы или заданных перемещений:

U i | s_u = U⁰,

• —    условие силового воздействия, при которых заданы компоненты вектора механических напряжений: t [ = *^U ^ У I s_t = P i ,

• —    условие гладкого контакта с абсолютно твердым телом — равенство нулю нормальных перемещений и касательных напряжений:

u „ = U i n i | s_ut = 0,t i ^(k) = (TijnjTi^WI_Sut = 0.

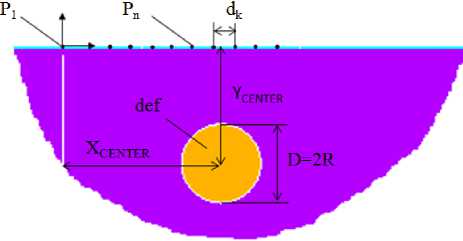
Описание модели. Рассматривается слоистая конструкция. Верхний слой жестко сцеплен с подстилающим полупространством (рис. 1). В слое 1 расположен дефект в виде круглой конфигурации с центром на определенной глубине. Свойства материала представлены в таблице 1. Дефект расположен на глубине Y loc = 1,5 м от поверхности и на расстоянии X loc = 2 м от точки P 1 приложения единичного импульсного P t (рис. 1) нагружения. Импульсное нагружение зависит линейно от времени приложения нагрузки (т = 0,003 с), что соответствует параметрам реального ударного нагружения (рис. 2). В качестве входного параметра рассматривается поле смещений поверхности в результате кратковременного импульсного воздействия. Радиус дефекта варьируется в расчетах как: R i = 0; 0,25; 0,3; 0,35; 0,4; 0,45; 0,5 м. В качестве базовой цели ставится определение функциональной зависимости радиуса дефекта от откликов колебаний, измеренных в определенных точках конструкции на основе применения ИНС.

Таблица 1

Параметры слоев

а)

Рис. 1. Модель слоистой конструкции с круглым внутренним дефектом: а — описание области с дефектом; b — cхема модели слоистой конструкции

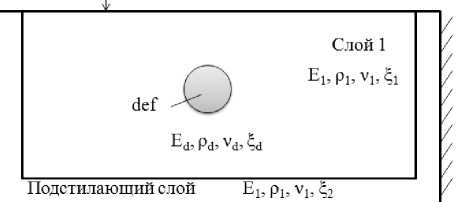
b)

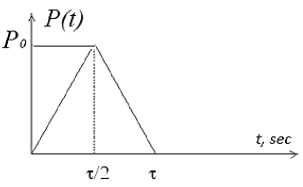
Рис. 2. Зависимость импульсной нагрузки P от времени нагружения

№	Наименование	Толщина, м	E, Гпа	ρ , кг/м 3	ν	Коэффициент затухания
1	Слой 1	5	0,1	2000	0,33	0,001
2	Подстилающий слой	0,1	0,1	2000	0,33	0,1
3	Дефект R i	X CENTER =2 YCENTER= –1,5	1	2000	0,33	0,001

КЭ моделирование. Моделирование плоской конструкции (ширина — 10 м ) с дефектом проведено в КЭ комплексе ANSYS : для моделирования применялись элементы типа PLANE82 с треугольной и четырехугольной конфигурацией с плоской деформацией ( 3950 узлов и 1890 конечных элементов). Внешний слой конструкции (подстилающий) имел большие коэффициенты демпфирования, но сохранял основные свойства слоя 1. Анализируемое время выбиралось таким, чтобы импульс от крайних границ конструкции не возвращался обратно. Это достигалось фиксацией времени резкого возрастания амплитуд колебаний у внешней границы слоя 1. Ударная нагрузка прикладывалась в точке P t на поверхности конструкции.

Вследствие импульсного нагружения возникают поперечные и продольные волновые смещения точек как на поверхности конструкции, так и по всему ее объёму. Пример формы поперечных колебаний конструкции в момент времени t = 0,01 c представлен на рис. 3. Контрольные точки (40 точек) расположены на поверхности на расстоянии dk = 0,1 м друг от друга (рис. 1). Имитация распределения точек на поверхности отображает реальную картину измерений. Первая точка измерений расположена на расстоянии 0, 1 м от места ударного воздействия.

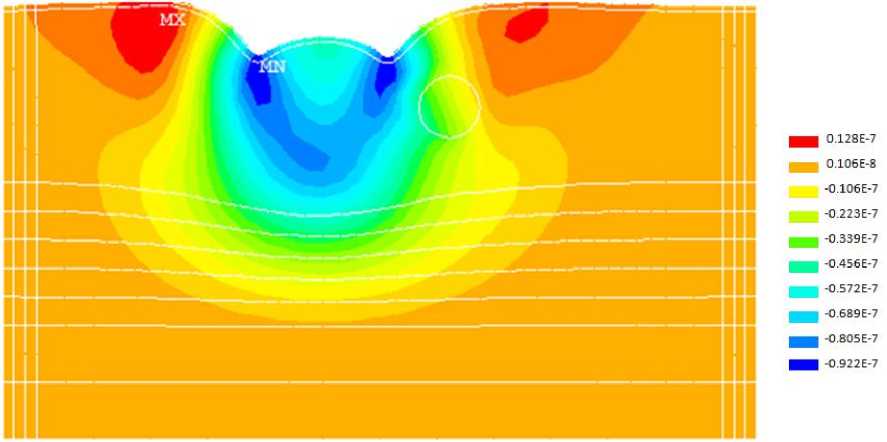
Рис. 3. Волновые смещения по толщине конструкции при t = 0,01 c

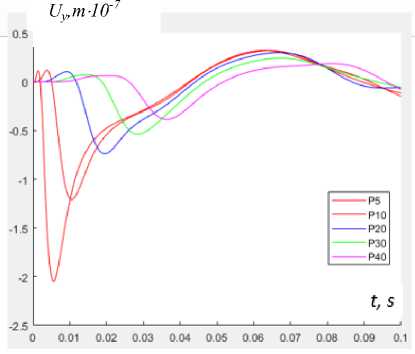
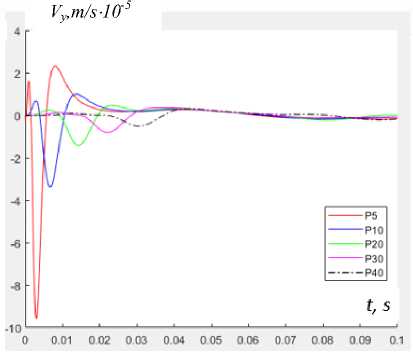
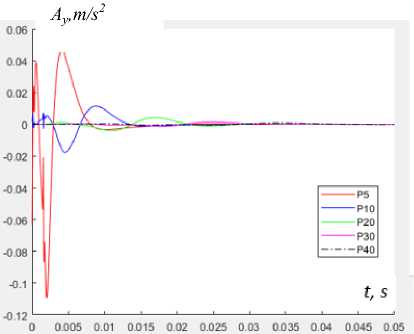
На рис. 4, 5 представлены результаты расчетов поперечных смещений (направление OY) в различных точках поверхности. В процессе решения задачи вычисляли поперечные смещения в контрольных точках конструкции на временном интервале t = 0–0,1 c. Особый интерес представляет поле смещений точек поверхностного слоя в промежутке времени t = 0–0,04 c. В данный период времени образуется первичная форма прогибов слоистой конструкции и отсутствуют отклики колебаний от возбуждения внешних слоев конструкции.

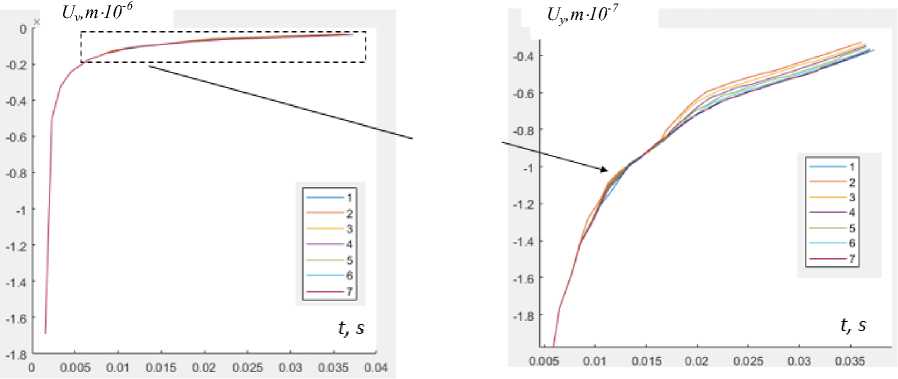
На рис. 5 приведены максимальные значения амплитуд колебаний в зависимости от времени их регистрации. Анализ показывает, что они имеют экспоненциальный приближенный тренд. Для одинаковых позиций измерения максимумов амплитуд имеются расхождения амплитуд колебаний в зависимости от величины радиуса дефекта.

На последующем этапе вычислены относительные значения смещения амплитуд Δ U y ( a ), скорости Δ V y ( b ) и ускорения Δ A y ( c ) для точек N p =1–40. Данные относительные значения вычислялись как разница между текущим показателем максимальной амплитуды для точки при R i (при i=2 - 7 ) и амплитудой параметра колебаний при размере дефекта R 1 =0 (отсутствие дефекта в конструкции) :

Δ U yi =U yi -U y1 ;

Механика

Δ V yi =V yi -V y1 ;

ΔA _yi=A_yi - A_y1.

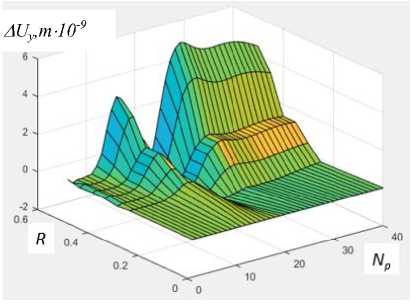
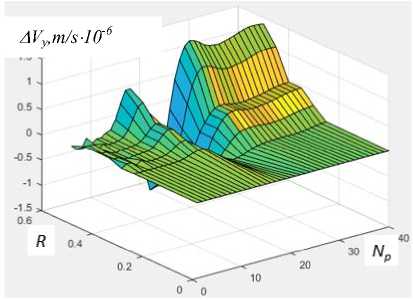
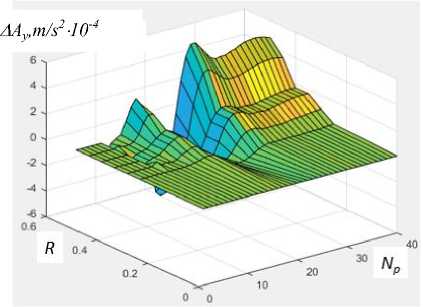
Ни рис. 6 приведены трехмерные графики, отображающие зависимости относительных величин смещения амплитуд Δ U y ( a ), скорости Δ V y ( b ) и ускорения Δ A y ( c ) для точек N p =1–40 на поверхности конструкции и варианта радиуса R i дефекта.

a)

b)

c)

Рис. 4. Амплитуды смещений U y (a) , скорости V y (b) и ускорения A y (c) в зависимости от времени для точек 1–40 на поверхности конструкции

a)

b)

Рис. 5. Зависимости максимальных перемещений:

а — от времени для точек 1–40 на поверхности конструкции для семи вариантов радиусов дефекта; b — для выделенной области амплитуд

∆ U y ,m ⋅ 10^-9

a)

b)

c)

Рис. 6. Относительные значения амплитуд смещения Δ U y (a) , скорости Δ V y (b) и ускорения Δ A y (c) для точек N p =1 – 40 на поверхности конструкции и варианта радиуса R i дефекта

Центр дефекта располагался под точкой P 20 . Анализ данных графиков показывает, что слева и справа в окрестностях дефекта возникают перегибы кривых максимальных амплитуд колебаний относительных значений перемещения Δ U y , скорости Δ V y и ускорения Δ A y . Эта тенденция сохраняется при всех вариациях радиуса дефекта R i . Этот признак тем самым может являться показателем локации дефекта. Такие эффекты на практике возможно достичь путем позиционного сканирования при регистрации и обработке амплитуд колебаний. Кривые относительных показателей перемещения, скорости и ускорения в окрестности дефекта достаточно хорошо коррелируют с величиной дефекта.

Применение нейросетевых технологий в задаче идентификации размеров скрытого дефекта. Установим связь между скоростью, ускорением и амплитудами колебаний, распространяющимися в слоистой структуре, и радиусом дефекта R i. . На основе полученных данных на этапе КЭ моделирования формируется обучающий набор, с помощью которого обучается построенная модель ИНС .

В результате численного решения ряда прямых задач в КЭ программном комплексе ANSYS были получены данные для 40 точек на поверхности слоистой структуры при вариациях радиуса дефекта R i. с ошибкой при вычислении в пределах 3% . Для каждого набора из 40 значений был установлен соответствующий радиус дефекта. Подготовленные обучающие вектора в качестве входных значений содержали относительные величины амплитуд колебаний ΔU y (N pi ) скорости ΔV y (N pi ) и ускорения ΔA y (N pi ) , а в качестве выходных значений — радиус дефекта. Всего было проведено 100 численных экспериментов. Таким образом, обучающая выборка состоит из 100 векторов для каждого типа исследуемого параметра ΔU y , ΔV y и ΔA y . Все данные, применяемые в обучении нейронной сети, нормализованы и находятся на интервале [0, 1].

Для идентификации радиуса дефектного включения применялась полносвязная многослойная модель ИНС , смоделированная в комплексе Matlab . Модель ИНС содержала 1 слой, состояла из 40 входных нейронов и 1 выходного нейрона. В качестве входной активационной функции выбиралась Sigmoid, а в качестве выходной активационной функции устанавливалась линейная зависимость. Сеть обучалась с помощью алгоритма обратного распространения ошибки на основе оптимизации Левенберга-Марквардта [37].

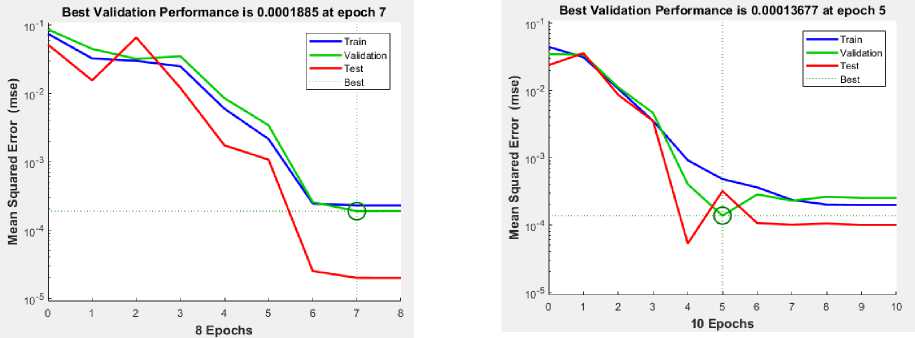
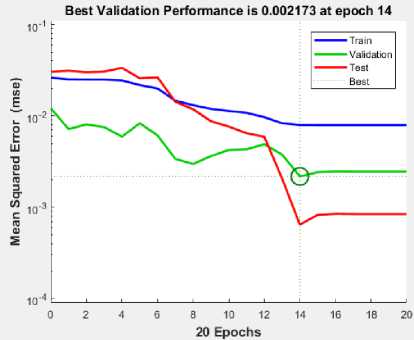
Функция потерь характеризовалась среднеквадратической ошибкой (MSE). Для обучающей и тестовой выборки было построено 100 векторов из показателей относительных величин амплитуд колебаний ΔUy, скорости ΔVy и ускорения ΔAy. Найдена корреляции данных параметров к радиусу дефекта. Установлено, что 8, 10 и 20 эпох обучения для соответствующих показателей достаточны для достижения необходимого уровня качества работы ИНС. На рис. 7 приведена зависимость cредне-квадратической ошибки от количества эпох обучения модели ИНС. Анализ показывает, что при достижении обучения более 8 эпох для всех относительных параметров амплитуд колебаний cредне-квадратическая ошибка (MSE) изменяется незначительно.

a)

b)

c)

Рис. 7. Изменение cредне-квадратической ошибки (MSE) работы ИНС в процессе её обучения на основе значений относительных величин колебаний: a — амплитуд Δ U y , b — скорости Δ V y и c — ускорения Δ A y

Таблица 2

Оценка точности вычислений

Используемая ИНС	Относительная ошибка, %
Δ U y	0,50
Δ V y	3,03
Δ A y	16,70

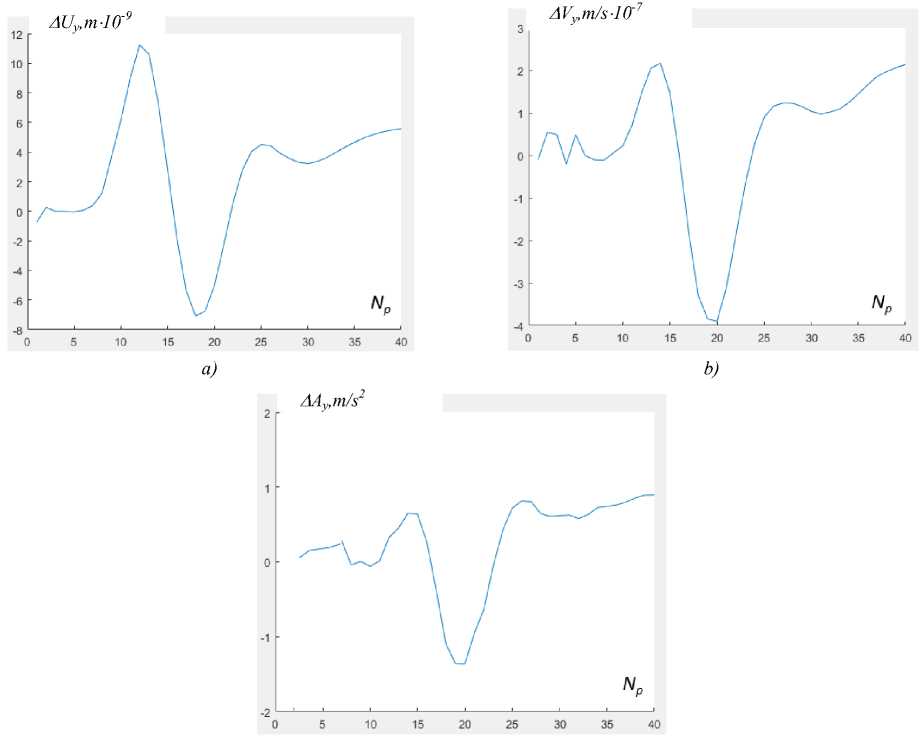
Тестирование полученных зависимостей ИНС . Для выборочной оценки восстановления показателя радиуса дефекта R i были выполнены наборы из параметров амплитуд колебаний и получены их относительные значения. Графическое отображение результатов трех тестовых наборов для относительных величин амплитуд колебаний Δ U y (a) , скорости Δ V y (b) и ускорения Δ A y (c) представлены на рис. 8. Данные показатели наборов подставляли в соответствующую ИНС и вычисляли значения радиуса дефекта. В таблице 2 приведена рассчитанная погрешность восстановленного радиуса R дефекта. Анализ показывает, что наименее точным является восстановление радиуса по параметрам ускорения. При этом средняя относительная ошибка восстановления параметра радиуса R дефекта на основе данных амплитуд колебаний Δ U y и скорости Δ V y не превосходит 5%.

c)

Рис. 8. Набор рассчитанных относительных величин амплитуд колебаний ΔU _y (a), скорости Δ V_y (b) и ускорения ΔA _y (c)

Обсуждение и заключения. Рассмотрена задача о восстановлении радиуса дефекта на основе применения имитационного моделирования колебаний в конечно-элементном комплексе ANSYS и ИНС в комплексе MATLAB . Получены результаты нестационарных колебаний полуплоскости с круглым внутренним дефектом. Вычислены поперечные смещения в контрольных точках конструкции при распространении волны от импульсного нагружения. В результате был разработан подход к восстановлению радиуса дефекта в конструкции на основе сочетания метода конечных элементов и ИНС . Наиболее удачная конфигурация архитектуры ИНС , состоящей из 1 скрытого и 1 выходного слоев, включала 40 входных нейронов и 1 выходной нейрон.

Исследование показало, что использованного объема данных достаточно для успешного обучения построенной модели и проведения идентификации скрытого дефекта конструкции. При этом относительная точность определения радиуса дефекта внутри слоя 1, в случае применения значений амплитуд колебаний перемещения и скорости, составляет более 99 %.

Таким образом построенные ИНС -алгоритмы могут успешно применяться для оценки стратификации слоистых конструкций при использовании временного и позиционного сканирования при возбуждении колебаний из дальней зоны.