Нейросетевое и алгебраическое моделирование параллельного 2D проецирования в волоконно-оптической томографии при ограниченном числе направлений сканирования

Для исследования, контроля и восстановления параметров физических полей (ФП), распределенных на протяженных поверхностях, все большее применение получают распределенные волоконнооптические измерительные сети (ВОИС). Такие сети представляют собой набор волоконно-оптических измерительных линий, уложенны х в соответствии с определенной схемой на исслед уемой поверхности. Задача восстановления параметров распределенных физических полей по характеристикам оптического излучения, проходящего по ВОИС, является томографической [3]. При решении томографической задачи одним из определяющих факторов является выбор схемы укладки измерительных линий.

Ранее для восстановления ф ункци й распределения ФП с помощью ВОИС измерительные линии (ИЛ) укладывались по четырем направлениям – горизонтальному, в ертикальному и двум диагональным (рис. 1 а ).

Рис. 1. Параллельные схемы укладки измерительных линий в ВОИС

Однако применение подобной схемы укладки линий при практическом изготовлении ВОИС большой размерности приводит к усложнению конструкции и методов обработки всей информационно-измерительной системы . Поэтому весьма актуальной является задача разработки эффективных конструкций ВОИС, позволяющих уменьшить число используемых ИЛ.

Целью настоящей работы является исследование конструкции распределенной ВОИС повышенной размерности, имеющей схему укладки ИЛ в трех направлениях (рис. 1 б ).

Задачу восстановления функций физических полей с использованием ВОИС можно разбить на несколько этапов: дискретизацию, получение и обработку проекционных данных, обратное проецирование (рис. 2).

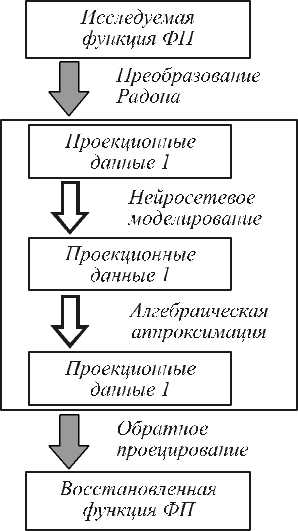
Рис. 2. Схема восстановления функции ФП

Основное внимание в этой работе уделено процессу обработки проекционных данных, который, в свою очередь, заключается в последовательном выполнении двух процессов:

• 1.    нейросетевой предобработки с помощью нейронной сети радиально-базисного типа,

• 2.    аппроксимации на множестве дискретизации специального вида, а именно: на объединении двух классов смежности.

1.    Основные определения и обозначения

Пусть через Z, R, C обозначены множества целых, вещественных и комплексных чисел соответственно. Далее будем предполагать, что f е С ” ( R ² ) , то есть фун кция f бесконечно дифференцируема и имеет компактный носитель, L ²( R ²) – пространство функций, интегрируемы х с квадратом над R ², S ( R ²) – пространство Шварца быстро убывающих ф ункций.

Пусть f ( x 1 , x 2 ) – функц ия двух переменных, описывающая исслед уемый объект.

Двумерное (2D) преобразование Радона отображает функцию f во множество ее линейных интегралов.

Пусть индекс i определяет направление сканирования φi, индекс j определяет отсчет sij в выбранном i – м направлении. В этом случае паре индексов (i, j) соответствует прямая линия Lij, вдоль которой сканируется область. Тогда значение проекции вдоль прямой Lij можно записать как gj = ^j f = f f (x1, x2 ) d 1,                      (1)

Lij где ^ - преобразование Радона функции f, ad 1 -приращение вдоль прямой Lij.

Пары чисел ( ф i , s ij ) , определяющие параллельную схему сканирования на плоскости, могут быть рассмотрены как элементы группы G = T х R , где интервал T = |^ 0, 2 л ) - циклическая группа относительно сложения по мод улю 2π, а R – аддитивная группа поля вещественных чисел [4].

Тогда функцию f можно представить в виде

N

f (x )=S fk ek (x) ■

k =1

Величина a j = ^j (ek (x)) = f ek (x) d 1 геомет-Lij рически представляет собой длину пересечения измерительной линии Lij с k-м элементом изображения Sk . Пусть p – число направлений сканирования, M – общее число измерительных линий и gii, gi2 , - , giY(i) значения всех y(i) проекций для i – го направления сканирования. В этом случае оче-p видно, что M = S y(i) ■ i=i

Интегральные уравнения (1) преобразуются в N систему M линейных уравнений S akfk = gj с N j=i неизвестными f1, ..., fN, которая в матричной форме имеет вид:

AF= G ,                                     (2)

где A = ( a ik ) 1^ i ^ M 1^ j ^ N - матрица размера M х N ,

F = ( f 1 , ..., f N ) ^т – столбец неизвестных высоты N,

G = ^{( g} 11 , ^g 12 ’"■, ^g 1y ( 1 ) ; ■■■ ; ^g i 1 , ^g i 2 ’"■, ^g i y ( i ) ; ■■■ ;

^g p 1 , ^g p 2 ^, ^, ^g p y( p ) )

столбец проекционных данных высоты M.

3.    Алгебраическая аппроксимация функции проекции

Спецификой задач волоконно-оптической томографии является наличие ультрамалоракурсной схемы сбора данных. Как правило, в таких ВОИС число измерительных линий меньше числа элементов контролируемых областей. Имеет место недоопреде-ленность системы линейных алгебраических уравнений (2). Таким образом, возникает проблема решения некорректной задачи [3], связанной с поиском решения по интегральным данным, получаемым по ВОИЛ, уложенным определенным образом на сканируемом поле. На практике часто встречаются схемы укладки измерительных линий, которым, с алгебраической точки зрения, не соответствуют решетки. К ним неприменимы обычные условия корректности. Примерами таких схем являются схемы, представленные на рис. 1 а , б .

Рассмотрим, например, схему укладки измерительных линий в четырех направлениях, при которой имеет место равномерное распределение углов

П k—, k = o,■■■,p-1 (рис 1 а)■ Особенностью этой p укладки является неравномерность отсчетов вдоль прямых: в вертикальном и горизонтальном направлениях шаг сканирования – h1, а в диагональных направлениях другой – h2 = 2 2 h1 .

Эту схему можно рассматривать как объединение двух стандартных подсхем с двумя направлениями сканирования (рис. 1 в, г), т.е. Лф = ^2 . При этом в плоскости Оф5 каждой из подсхем соответствует своё множество дискретизации. Первой соответствует множество дискретизации М1, а второй – М2 . С алгебраической точки зрения, эти множества дискретизации имеют различные структуры. Так, множество М1 является решеткой, М1 = H1, где Н1 - подгруппа, порож- денная над Z 2

( V матрицей W 1 = I о

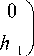
т.е.

Н1 = W 1 Z2, Множество М2 решеткой не является, но его можно представить как смежный класс дискретной группы G по подгруппе

Н₂ = W ₂ Z ², W ₂

Г /2 о ) 1 0 h 2 J

Таким образом, множество вида м = м 1 и м 2 = h1 U Ж +

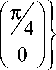
представляет собой множество дискретизации для всей исслед уемой схемы сканирования (рис. 1 а ) в четырех направлениях.

Очевидно, что множество дискретизации M не удовлетворяет обычным условиям дискретизации, поэтому невозможно непосредственно использовать стандартны е алгоритмы без опасности получить серьезные артефакты.

Если R1 и R2 – фундаментальные области решеток Hf и И2 соответственно, то имеет место оче видное включение R1 с R2.

Это говорит о том, что решетка Н2 является более плотной и множество дискретизации М2 целесообразно взять в качестве основного для восстановления ф ункции проекции по формуле g (z ) = SH2 + x2 g ( z) + (1 — e2m

X Z yg Hi

g ( У )^SH2 + x 2 g ( У )

X R1< z^_У)

1 _ e^2п‘<У^_x . v)

для любого z g G и Ci = (2л) ¹ |W-|, i=1,2.

В формуле (4) xr. — обратное преобразование Фурье характеристической функции х_R фундаментальной области Ri ([ 5-7]).

Первое слагаемое в (4) представляет собой аппроксимацию на множестве M2 и вычисляется по формуле виде объединения двух однотипных двумерных решеток (3) и затем применить формулу (4).

Для того, чтобы это стало возможным, не хватает значений четвертого направления сканирования и их предполагается получить, применив RBFNN.

На рис. 2 представлена схема восстановления функц ий физических полей с помощью распределенной ВОИС. В соответствии с этой схемой неполные проекционные данные 1 преобразуются нейросетевым методом в более полный набор проекционных данных 2.

4.    Использование нейронных сетей RBFNN

Ранее в работе [8] авторами была исследована возможность применения RBFNN для схемы укладки в трех направлениях (рис. 1б).

Формируемый сетью информационный массив, представленный вектором G, являлся набором томографических данны х, по которым нейронная сеть должна реконструировать вектор F. Таким образом, нейросеть должна выполнить преобразование вида F = A (G), предварительно пройдя обучение на множестве об учающих пар {(G, F)}.

Для создания обучающей страницы использовался способ выбора обучающих пар «с подкреплением», при котором рассматривались пары вида (Gi , Fi), где AFi= Gi.

При создании обучающих пар RBFNN в [8] использовались функци и гауссовского типа _v ( \ ^_Ц(^x_ci)2 ⁺(у^_bi)²) ,

Z (x, y) = e ' ', причем параметры bi, ci, являющиеся центрами данных RBFNN, подбирались как узлы решетки соответствующей схемы сканирования.

Были использованы эталонные распределения: одиночные Гауссианы и пары Гауссиан.

Для поля 5×5 была составлена обучающая страница, состоящая из 3325 обучающих пар, на которой была обучена сеть RBFNN. Экспериментально было показано, что построенная сеть позволяет осуществлять восстановление функций пространственного распределения исслед уемой физической в еличины с погрешностью в отдельной точке не более 2%, обладает хорошими прогнозирующими возможностями. Однако было отмечено, что при этом способе восстановления в задачах с применением ВОИС повышенных размерностей возникают серьезны е трудности при об учении сети ввид у слишком большого объема обучающих страниц. Поэтому возникла необходимость поиска оптимальных путей при применении нейронных сетей.

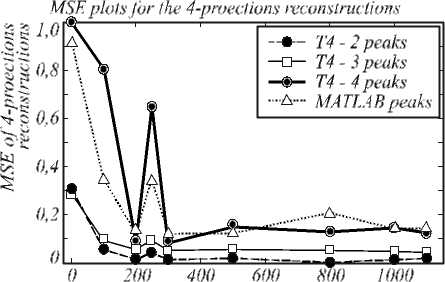
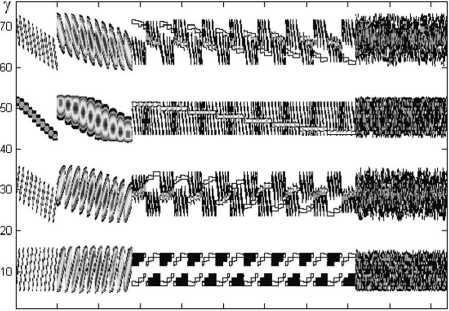
5.    Использование нейронных сетей RBFNN для предобработки проекционных данных

Опишем теперь более подробно нейросетевой метод предобработки проекционных данных. Обозначим через ^i набор томографических данных по i-му направлению сканирования:

^. =(g1, gi2 ,”, giy(i)) , ^{1 5}i⁵P .

Предположим, что практически возможно получить значения данных только для p-1 направления сканирования ^1,$₂,..., ^_p ,, а для корректного восстановления функции f (x1, x₂) классическими или специальными методами (например, ART, FBP [9], UQC 1 или UQC 2 [6, 7]) необходимо иметь значения проекционных данных в p направлениях ^1 ,Я₂,... ,^p-1, ^p .

Следовательно, в первую очередь, необходимо получить значения проекционных данны х с недостающего p – го направления сканирования.

Для решения этой задачи предлагается использовать нейронную сеть радиально-базисного типа, которая должна выполнить преобразование вида

^1 ,^2,..., ^p-1 p .

Выбор эталонных функций должен находиться в зависимости от ширины спектра b исслед уемой функц ии f (x,y). Ф ункц ии гауссовского типа

^-“i(⁽x - ^⁺⁽У - bi))

Z (x, у ) = e ' ¹ (5) могут быть использованы в качестве таковых, так как они принимают ненулевые значения только в зоне вокруг определённого центра.

Для проведения анализа нейросетевого метода решения задачи с помощью RBFNN в этой работе была рассмотрен а томографическая зад ача восстановления информации с информационно-измерительного поля размерности 10×10 и выше. Предполагалось, что эталон ное воздействие на поле имеет вид гладкой функции с ограниченной эффектив ной шириной спектра b, равной условной спектральной единице п. Можно также считать, что все значения функции неотрицательны и нормированы на единицу.

В данной работе использованы те же три типа эталонных распределений физической величины, что и в [8]. Первый и второй типы относятся к регулярному способу, а третий – к случайному. Опишем их подробнее.

Тип I. Эталонные распределения поля в этом случае представляют собой одиночные Гауссианы вида (5), центры которых расположены в узлах измерительной сети.

Параметр ai отвечает за ширину носителя функции Z(x,y). Если исслед уемая ф ункция f имеет ширину спектра b = п, то по теореме Найквиста правильное восстановление ф ункции возможно, если шаг сканирования h 51. Тогда ширина носителя функц ии Z(x,y) должна быть порядка 2 h . Следовательно, и ширина носителя ф ункции должна быть того же порядка. Было установлено, что оптимальными для обучения являются параметры ai, принимающие значения 0 < a_i 5 5 .

Для обучения рассматривались одиночные Гауссианы:

• a)    Узкие одиночные Гаусси аны ai = 1, 2 ,... , 5.

• б)    Широкие одиночные Гауссианы ai = 0,1; 0,2;...; 0,9.

Тип II. Аналитически эти ф ункции могут быть представлены в виде

,                - a 1 (⁽x - c 1 J" ⁺⁽У - ^Ь1 J" }       " a 2 (⁽x - c 2 ^{)2 + (}У - ^Ь 2 ⁾²}

Z(x, у) = e^v' + e^v'        (6)

при условии, что носители находятся на расстоянии не менее 2п / b , т.е.

V(^b1-^b2 )2 ⁺ (^C1—^C2 )2

2 2a1 2 2a2

п

>2-. b

Это пары Гауссиан с непересекающимися носи- телями.

Тип III. Эталонные распределения этого типа были получены с помощью процесса рандомизаци и с нормированием. Каждому целочисленному случайному набору a1, а2, b1, c1, b2, c2 = 1,N ставилась в соответствие функ ция вида (6). Каждый вектор перед включением в обучающую страницу был нормирован.

6.    Создание обучающей страницы

Качество обучения RBFNN зависит от правильного подбора обучающих пар, которые составляют обучающую страницу.

Для каждой эталонной функ ции Z(x,y) находим проекции по всем p направлениям сканирования и строим вектор-столбец

^{G    (g} 11, ^g 12 ’"•, ^g 1у(1); ... ; ^gi 1, ^gi 2 ’"•, ^giy( i); ... ;

gp ,1, gp ,2 ,-, gp ,y( p)) T =№ ... ^i... ^p ) T .

Повторяем эту процед уру для всех эталонных функций.

Пусть M – количество функций в обучающей странице, а Q – матрица, состоящая из столбцов проекционных данных для всех M ф ункций обучающей страницы:

	' ^(1J   ^(2)   - ^(M)Л
	^(1)   ^(2)- ^(M)		Q
Q=	:   --		^.
	^(1)   ^(2)   - ^(M >
	p-1       p-1             p-1
	ч^p1»   ^p2>  -  ^pM) ?	} Q2
Матрицу,     состоящую		из     первых

у(1) +-----+ y(p -1) строк матрицы Q, обозначим че рез Q1, а из последних y(p) — через Q2.

Таким образом, созданы два массива для обучения нейронной сети: Q1 – массив входных данных из M векторов длины у (1) +-----+ у( p -1), а Q2 - массив со ответствующих выходов изMвекторов длины у(p).

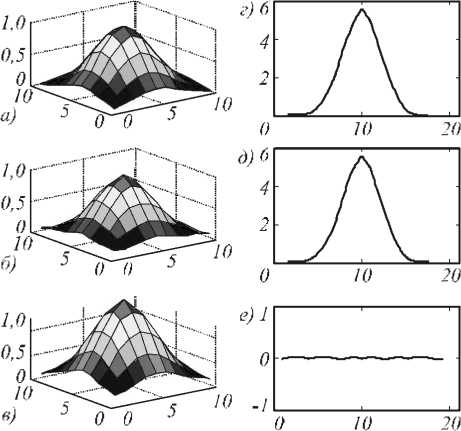
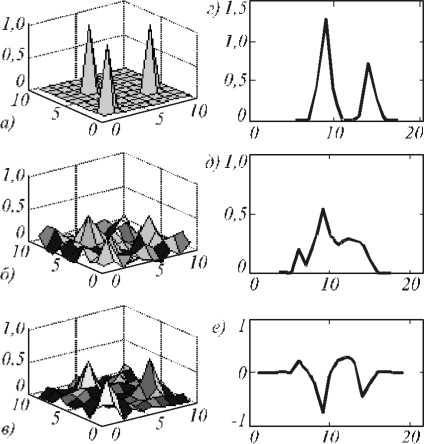
7.    Восстановление функции проекции на объединении двух множеств дискретизации

После того, как проекционные данные были обработаны с помощью нейросетевых методов, они приобрели корректны й вид для применения к ним алгебраических методов, кратко изложенных в п. 2.

Далее восстановим функцию проекций g = ^ f алгебраическим методом, подробно изложенным авторами в работах [6, 7], основанным на применении формулы (4).

Алгоритм:

• 1.    Создание массивов проекционных данных.

• 2.    Создание массива измерительных данных по наиболее плотному множеств у дискретизации. Массив формируется из проекционных данных по наиболее плотному множеству дискретизации M 2 = H 2 + X 2 .

• 3.    Аппроксимация и коррекция проекционных данных по менее плотному множеств у дискретизации M₁ .

• 4.    Комбинация измерительных и проекционных данных.

• 5.    Создание массива дополнительных данны х, используя сдвиги данных из п. 2 и п. 3 на половинные углы.

• 6.    Комбинация данных из п. 4 и п. 5.

8.    Численное моделирование

След ующие два шага при необходимости можно применить с целью дальнейшего увеличения числа проекционных данных.

Далее выполняется ст андартная процедура обратного проецирования в соответствии со схемой, представленной на рис. 2.

Для проведения анализа нейросетевого метода решения задачи с помощью радиально-базисной нейронной сети было рассмотрено информационноизмерительное поле 10×10 (n=10).

Эталонные распределения (п. 3.3) для поля10×10 имеют след ующий вид:

• 1)    узкие и широкие одиночные Гауссианы представлены в 500 и 900 вариантах соответственно;

• 2)    пары Гауссиан с непересекающимися носителями были найдены в среде Matlab в количестве 2688 функций (ai =3, 5; bi , ci = 2,9 );

• 3)    эталонные распределения, полученные рандомизацией с нормированием, выбирались в количестве L функций по случайному набору параметров a1, а2 = 1,5 , b1, c1, b2, c2 = 1,10 .

По этим наборам эталонных распределений составлялись матрицы проекционных данных, из которых далее формировались вход и выход нейронной сети. Сеть обучали несколько раз для различных значений рандомизированных распределений L: 0 < L< 1100.

На рис. 3 представлены зависимости нормированной среднеквадратичной ошибки (mse) от L для восстановления недостающей четвертой проекции для четырех типов распределений, не принадлежащих обучающей странице.

(КкяНОО

Рис.3. Зависимости нормированных среднеквадратичных ошибок для восстановления функций проекций от числа рандомизированных функций в обучающих страницах

На рис. 4 изображены зависимости mse восстановления функции распределения физического поля от объема обучающей страницы. Пунктирная и сплошная тонкая линии соответствуют функциям из обучающей страницы, а остальные – двойным, тройным и четверным комбинациям Гауссиан.

Plots of reconstruction errors tor testing functions

0,035^

0,030-"^

О 0,020-

§ 0,015 «►*<$■

«—8>

o.oio *84.....* *•

*-

• — о— ТЗ   - 2 peaks

• - -•■- T1,T2- 1 peak

• — *■■■■ T4   -2 peaks

• - *8^- T4   - 3 peaks

  -&- 14  - 4 peaks

  -A—A"

■в----@—®"

*............* *

0    200   400   600   800 1000

0

Рис.4. Зависимости нормированных среднеквадратичных ошибок для восстановления функции распределения физического поля от объема обучающих страниц

На основании проведенных численных экспериментов был сделан вывод о том, что оптимальным является параметр L = 500.

На рис. 5 для L = 500 изображен контур проекционных данных, использованных для обучения.

Для сети, обученной на 4588 обучающих парах, величина mse по обучающей странице не превысила величины 6,7 × 10-16.

На рис. 6 приводится исследование для эталон-

-0.1((x-4)²+(y-6))

ной функции вида: Z(x, y) = e

Как следствие, мала и ошибка восстановления

-0.1(( x -4)²+(y-6)²)

исследуемой функции Z(x, y) = e

500   1000 1500 2000 2500 3000 3500 4000 4500 Т

Рис.5. Контур множества проекционных данных для создания обучающей страницы

Рис. 6. Эталон (а), восстановление с помощью классического метода фильтрации обратных проекций (FBP) (б), оригинал проекции № 4 (под углом 135^о) (г), восстановление проекции № 4 с помощью нейронной сети RBFNN (д), ошибка (mse) восстановления функции проекции четвертого направления (е)

Проекционные данные этой функции используются при создании об учающей страницы.

Для функции в левом столбце рис. 6 приведены результаты восстановления с помощью последовательного применения нейросетевого и алгебраического методов с последующим обратным проецированием.

В правом столбце на рис. 6 представлены результаты нейросетевой предобработки функции проекции: показаны результаты восстановления значени й с недостающего направления сканирования.

При RBF-восстановлении 4-го направления сканирования ошибка близка к нулю и равна 3,7484×10-24.

Аналогичная ситуация для других ф ункций из обучающей страницы.

Для функций, не принадлежащих обучающей странице, значения mse при восстановлении функции проекции уже не нулевые (рис. 7е).

Так, для фун кции

• - 5 ((х-2)²+(у-2)²) -5 ((х-4)²+(у-7)²) -5 ((х-8)²+ (у-4)²)

Z (х, у) = e + e + e , которая соответствует воздействию на исслед уемое поле в трех различных местах, при RBF-восстановлении 4-го направления сканирования mse равна 0,0568, а итоговая ошибка восстановления самой функции – 0,0145.

Рис. 7. Восстановление функции, не принадлежащей обучающей странице (обозначения а-e соответствуют обозначениям, использованным на рис. 6)

Однако, следует заметить, что функция проекции, построенная с помощью нейронной сети (рис. 7д), похожа на исходную проекцию (рис. 7г), но имеет более сглаженный вид. Это вполне соответствует общей концепции обучаемости нейронной сети.

Заключение

В статье представлены основные принципы решения нелинейных задач реконструктивной томографии для восстановления информации, поступающей с волоконно-оптических измерительных линий распределенной ВОИС. Предложен новый комбинированный алгоритм обработки проекционных данных для реконструкции ф ункций распределения физических полей.

Этот алгоритм заключается в последовательном выполнении двух процессов: нейросетевой предобработки измерительной информации с помощью RBFNN и дальнейшей аппроксимации полученных данных на множестве дискретизации специального вида.

При реализации RBFNN предложен новый способ создания функций для обучения нейронной сети, которые строятся на основе тех функций, которые моделируют конкретный физический процесс. Построенная сеть обладает хорошими прогнозирующими возможностями и может с успехом использоваться для распределенных вычислений в задачах с применением ВОЛС больших размерностей. В результате применения нейронной сети происходит восстановление проекционных данных с недостающих направлений сканирования, что предоставляет возможно сть примене- ния методов аппроксимации данных на нерегулярной сетке специального вида.

Применение комбинированного алгоритма позволяет восстанавливать информацию с полей вдвое более высоких размерностей по сравнению с ранее использованными методами [8].