Нейросетевой анализ нормальности малых выборок биометрических данных с использованием Хи-квадрат критерия и критериев Андерсона - Дарлинга

Экспериментально полученных данных часто бывает недостаточно. Например, медику, чтобы получить данные 20 пациентов с одним и тем же заболеванием, может потребоваться лечебная практика длительностью 1 год и более. При этом проверить нормальность данных на столь малых выборках невозможно. Если пользоваться стандартными статистическими рекомендациями1, то для проверки гипотезы нормальности потребуется выборка из 200 и более опытов. Обычный врач сможет самостоятельно получить такое количество данных не менее чем за 10 лет практики.

Схожая ситуация возникает у биологов, а также при сборе биометрических данных. И медики, и биологи прежде были вынуждены ждать, когда у них появится достаточно большая выборка. Ситуация начала меняться с развитием биометрии. Люди негативно относятся к тому, что при обучении нейронных сетей им придется 200 раз приложить палец к сканеру или 200 раз записать рукописный пароль. Однако пользователи согласны приложить к сканеру папиллярного рисунка свой палец 20 раз или 20 раз записать пароль. По этой причине в нейросетевой биометрии серьезное внимание уделяется разработке новых методов, позволяющих проверять статистические гипотезы на выборках малого объема.

Обзор литературы

В 1900 г. К. Пирсон создал хи-квадрат критерий, который на целое столетие определил вектор развития теории математической статистики2. В середине ХХ в. появились первые исследования, посвященные синтезу искусственных нейронных сетей, ориентированных на эффективное распознавание образов. Вторая половина ХХ в. была посвящена тому, чтобы добиться эффективного обучения искусственных нейронных сетей. Только в начале ХХI в. удалось достичь промышленного применения технологии обучения искусственных нейронных сетей. Каждый цифровой фотоаппарат сейчас имеет нейросетевое приложение, отыскивающее в кадре лица людей3. Автоматическое обучение искусственных нейронных сетей нейросетевых преобразователей биометрических образов в код криптографического ключа аутентификации регламентируется в России национальным стандартом4. Биометрия – особый сегмент рынка, подлежащий специальному регулированию. На данный момент международное сообщество разработало порядка 120 биометрических стандартов, из которых 44 адаптированы к русскому языку и введены в действие в России.

Хи-квадрат критерий и другие известные статистические критерии при проверке статистических гипотез ориентированы на сравнение экспериментальной функции вероятности P ( x ) с теоретической функцией вероятности P ( x ). Фактически все статистические критерии решают ту же задачу, что и обычные нейроны, то есть для каждого из известных статистических критериев может быть построен свой искусственный нейрон. В частности, для хи-квадрат критерия эквивалентный искусственный нейрон будет описываться следующими преобразованиями для выборки объемом в 21 опыт при гистограмме из 5 равных интервалов:

x ^ sort ( x )

2 ^c

5          ( ⁽ xi + 1 )      ⁽ xi ЛМ

^y 121

^    ( P ( X i + 1 ) - P ( X i ) )     , ( )

z ^ "0" if c ² <  0.375

z ^ "1" if c ² >  0.375

где n_i – число опытов, попавших в i -й интервал гистограммы.

В работоспособности квадратичного нейрона (1) можно убедиться благодаря результатам имитационного моделирования, приведенным на рис. 1.

Результаты (рис. 1) показывают, что отклики нейрона на данные с нормальным законом распределения и отклики на данные с равномерным законом существенно отличаются. При квантовании выходных данных сумматора нейрона по порогу 0,375 вероятности ошибок первого и второго рода оказываются равными: P ₁ = P ₂ = P_ЕЕ = 0,288.

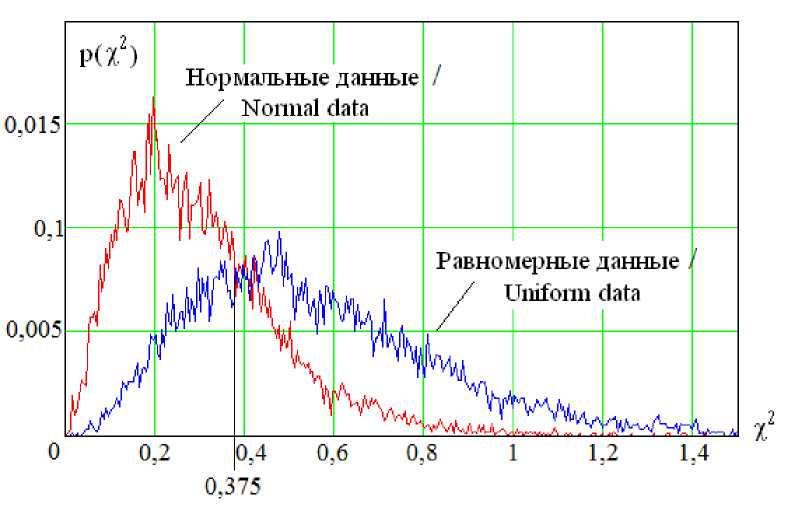
Р и с. 1. Отклик хи-квадрат нейрона при выборке в 21 опыт для данных с нормальным и равномерным распределениями

F i g. 1. The response to the chi-square of a neuron when sampling 21 experiments for data with normal and uniform distributions

Идеи К. Пирсона были активно поддержаны математическим сообществом; в ХХ в. были созданы десятки различных статистических критериев5. В частности, в 1952 г. был разработан критерий Андерсона – Дарлинга. Нейрон, эквивалентный данному критерию, описывается следующими преобразованиями:

х ^ sort ( х )

ad ₂ ^ £ { . - 21 . P⁽х. ) } ² ^ ( 1 - P ( x ) ) . P ( х . ), z ^ "0" if ad ² <  232 z ^ "1" if ad ² >  232

Об эффективности работы нейрона Андерсона – Дарлинга можно судить по данным имитационного моделирования, приведенным на рис. 2.

Видно, что отклики нейрона на данные с нормальным законом распределения и отклики на данные с равномерным законом существенно отличаются. При квантовании выходных данных сумматора нейрона по порогу 232 вероятности ошибок первого и второго рода оказываются равными: P ₁ = P ₂ = P_ЕЕ = 0,349.

Очевидно, что для малой выборки (21 опыт) мощность хи-квадрат критерия выше мощности критерия Андерсона – Дарлинга примерно на 21 %. Подобный эффект достигается выполнением следующего неравенства:

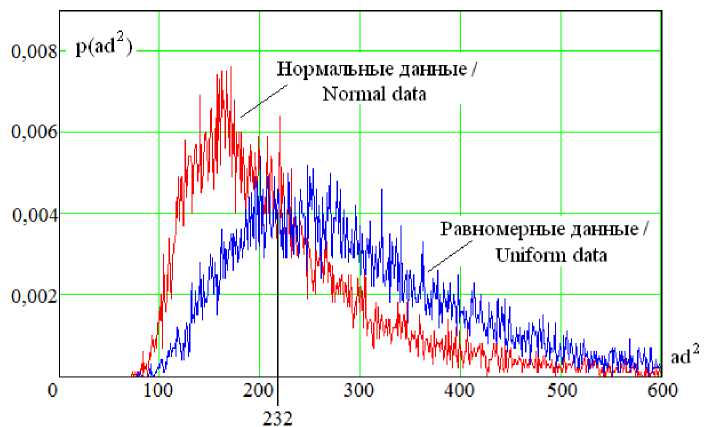
Р и с. 2. Отклик нейрона Андерсона – Дарлинга при выборке в 21 опыт для данных с нормальным и равномерным распределениями

F i g. 2. The response of the Anderson–Darling neuron in a sample of 21 experiments for data with normal and uniform distributions

P_ЕЕ ( χ ²) = 0,288 <  P_ЕЕ ( ad ²) = 0,349. Если руководствоваться принципом бритвы Оккама, нужно использовать только хи-квадрат критерий, отбросив данные критерия Андерсона – Дарлинга. В настоящее время такой подход нерационален, так как мы можем совместно использовать два нейрона, как это принято в российской нейросетевой биометрии⁶ [1; 2]. Такая возможность обусловлена низким уровнем коррелированности выходных данных двух рассматриваемых критериев: corr ( χ ², ad ²) = 0,423.

Если мы объединяем два нейрона, то они должны принимать состояния «00» и «01» для признания данных нормальными. Два других состояния («11» и «10») будем трактовать как признание предъявленных данных равномерными. В представленной ситуации вероятность ошибок снижается примерно на 20 %: с 0,288 до 0,239.

Соотношение (2) построено с опорой на аналитическую запись критерия Андерсона – Дарлинга, однако может быть выполнен переход к логарифмической форме записи данного критерия. Нейрон, соответствующий логарифмической форме записи, описывается системой следующих преобразований:

x ^ sort ( x )

20 i + 1

adL ^ 2{    ■ ln( P ( x )) +

i=0  21

+ [ 1 - i ^j ^ ln(1 - P ( x )) } . (3)

z ^ "0" if adL < 10.705

z ^ "1" if adL >  10.705

На рис. 3 даны распределения откликов нейрона логарифмической формы Андерсона – Дарлинга.

При значении порога квантования 10,705 совпадают значения вероятностей ошибок первого и второго рода: P ₁ = P ₂ = = P_ЕЕ = 0,32. Значение данной величины меньше аналогичного значения нейросетевой реализации классической формы Андерсона – Дарлинга (2). Кроме того, данные две формы нейронов имеют в своих откликах независимые составляющие: corr ( ad ², adL ) = 0,644. Фактически мы имеем два разных статистических критерия, дополняющих друг друга.

Объединенное использование хи-квадрат нейрона (1) и логарифмической формы нейрона (2) позволяет снизить вероятность ошибок до 0,236. Одновременное использование двух вариантов критерия Андерсона – Дарлинга и хи-квадрат критерия дает дополнительное, но незначительное снижение вероятности ошибок до 0,231.

Материалы и методы

Средневековый принцип бритвы Оккама является оправданием множества процедур обхода «проклятия» размерности за счет понижения размерности задачи. Например, это может быть сделано методом главных компонент, созданным К. Пирсоном в 1901 г. Метод главных компонент является практической реализацией доказанной в 1947 г. теоремы Карунена – Лоэва7 [3].

Обоснование бритвы Оккама методом главных компонент кажется оптимальным, однако оно актуально лишь для линейных функционалов (только для линейной алгебры). Если мы строим нелинейную алгебру нейросетевых функционалов, все оказывается сложнее, что мы и постарались продемонстрировать. Бритва Оккама требует отбросить два варианта критериев Андерсона – Дарлинга и пользоваться только хи-квадрат критерием как самым информативным. Однако объединение всех трех крите-

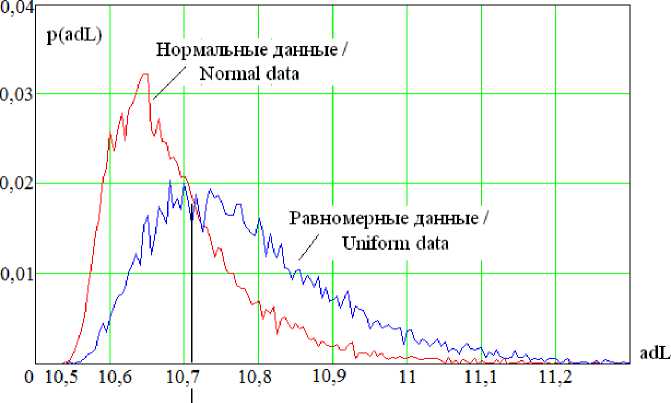
10,705

Р и с. 3. Отклик логарифмической формы нейрона Андерсона – Дарлинга при выборке в 21 опыт для данных с нормальным и равномерным распределениями

F i g. 3. The response of the logarithmic form of the Anderson–Darling neuron in a sample of 21 experiments for data with normal and uniform distributions риев одним слоем искусственных нейронов и корректировка выходного кода дает положительный результат: данные, которые необходимо было отбросить, удается объединить. Обобщенная структура этого направления синтеза новых процедур статистической обработки отображена на рис. 4.

Могут быть построены десятки нейронов, воспроизводящих работу известных и новых статистических критериев. При этом каждый из нейронов будет обладать своей относительной мощностью разделения нормальных и равномерных данных. Для статистических критериев, уже имеющих программные нейроны-аналоги, данные имитационного моделирования приведены в табл. 1.

Данные в табл. 1 показывают, что наиболее информативным является дифференциальный вариант критерия среднего геометрического8:

x — sort ( x )

21 /Т +1 sg d ■ V       ■ Р ⁽ x i )

i=1 21          , z - "0" if sgd < 7.45 .z - "1" if sgd > 7.45

где p ( x ) - значение плотности распре- 9 P ( X; )

деления или производная---- i функ- ¶ x

ции вероятности.

Вторым по уровню информативности оказывается хи-квадрат нейрон (1), третьим - нейрон Смирнова - Крамера – фон Мизеса:

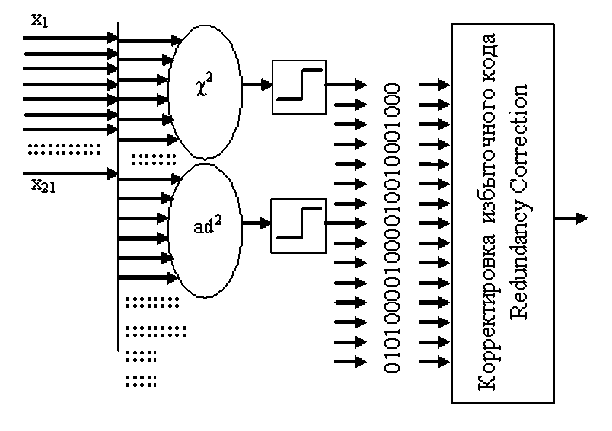
Р и с. 4. Обобщение большого числа статистических критериев однослойной сетью искусственных нейронов (аналогия с нейросетевыми преобразователями биометрия-код, выполненными в соответствии с российскими стандартами пакета ГОСТ Р 52633.хх)

F i g. 4. Generalizing of a large number of statistical criteria with a single-layer network of artificial neurons (analogy with neural network biometrics-code converters made in accordance with the Russian standards of the GOST R 52633.xx package)

Т а б л и ц а 1

T a b l e 1

Данные о значениях ошибок первого и второго рода для различных статистических критериев с оценкой порядка их следования по уровню их информативности

Data on the values of the errors of the first and second kinds for various statistical criteria with an assessment of the order of their sequence in terms of their informativeness

Критерий / Criterion P EE Информативность / Informativeness χ2 0,288 2 ad2(2) 0,349 6 adL (3) 0,320 4 sg 0,320 4 sgd 0,278 1 ω2 0,351 7 ω2c 0,311 3 su2 0,322 5 x — sort (x)

21                             2

w c ^-gB^⁽Я . (5) z - "0" ifsg d < 31.6

_ z - "Vifsg_d >  31.6

Четвертое место по информативности принадлежит логарифмической форме нейрона Андерсона – Дарлинга (3) и интегральному варианту критерия среднего геометрического9 [4]:

x ^ sort ( x )

x ^ sort ( x )

₂      1                       J²

^su ^ ; ( x )l i =0 a i'(^x2^1-- - x i. (7)

z ^ "0" if su ² <19.88

z ^ "1" if su ² >19.88

Наиболее низкой информативностью из рассмотренных обладает нейрон, воспроизводящий наиболее раннюю версию критерия Крамера – фон Мизеса, созданную в 1928 г.11:

x ^ sort ( x )

21 i +1

sg ^ 2      -^{(1 -} P (x i ) )

i =1     ²¹

z ^ "0" if sg < 8.52

. z ^ "1" ifsg >  8.52

w

^hov

P ( x )- ^ +1

i 21

x +1 — x i x ₂₀ ^- x 0 .

. (8)

z ^ "0"	if w 2	< 0.0043
z ^ "1"	if w 2	> 0.0043

Пятое место по информативности независимого применения занимают нейроны Шапиро – Уилка10:

Принципиально важным является то, что на данный момент созданы десятки различных статистических критериев, то есть длина выходного избыточного кода нейронной сети (рис. 4) достаточно велика. Если подавать нормальные данные на нейронную сеть, она будет откликаться кодами с большинством нулевых разрядов, то есть корректоры редких ошибок избыточных кодов оказываются достаточно примитивными. При их создании может быть использован опыт разработки подобных корректоров кода для биометрических приложений [5–8].

Во времена Пирсона не существовало вычислительных машин и искусственных нейронов. В настоящее время ситуация изменилась коренным образом: могут быть созданы программные продукты, комплексно учитывающие десятки и даже сотни статистических критериев. Все это позволяет ожидать появления в ближайшем будущем статистических программ, позволяющих с очень высокой точностью выполнять прогнозы на малых выборках. Если сейчас для достоверного принятия решений о нормальности закона распределения требуются выборки в 200 опытов, то в скором времени появятся прецизионные средства статистических оценок для выборок в 20 опытов. Все это является следствием перехода от попыток обобщений в линейных пространствах к многомерным нейросетевым обобщениям.

Результаты исследования

Следует отметить, что удовлетворительной теории кодов, корректирующих ошибки искусственных нейронных сетей, пока не существует, а классические самокорректирующиеся коды дают низкие результаты. Вместо создания новой теории корректирующих свойств гибрида нейронной сети и избыточного самокорректирующегося кода необходимо переходить от однослойных нейронных сетей к многослойным.

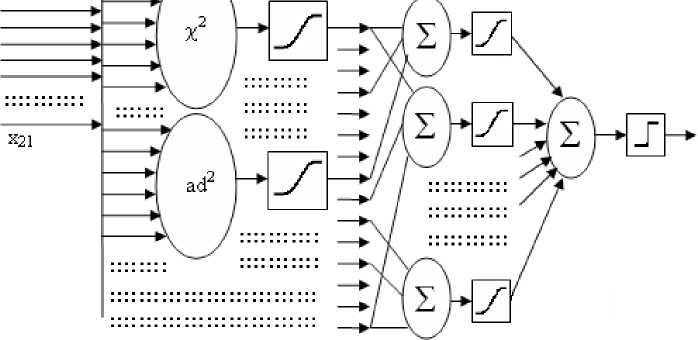
Следует отметить, что впервые многослойные нейронные сети начал обу- чать А. И. Галушкин12, создав в 1974 г. метод обратного распространения ошибок. На тот момент реализовать данный метод для многослойных нейронных сетей было технически невозможно. Ситуация изменилась только через 10 лет, когда Дж. Хинтон предложил обучать первые слои нейронов машинами Больцмана [9]. В конечном итоге это и позволило получить в XXI в. промышленно применимый алгоритм обучения глубоких нейронных сетей [10]. В таком контексте промышленно применяемые алгоритмы обучения можно называть алгоритмом Галушкина – Хинтона. Их применение позволяет обучать любые «глубокие» нейронные сети13 (например, сеть со структурой, приведенной на рис. 5).

Сеть на рис. 5 имеет три слоя нейронов, при этом нейроны первого и второго слоя должны быть гладкими. Только один выходной нейрон всей «глубокой» сети имеет полностью дискретный квантователь.

Потенциальное качество работы нейронов второго слоя «глубокой» сети зависит от числа входов нейрона, от качества его входных данных и от их взаимной коррелированности.

Значения взаимной корреляции нейронов первого слоя приведены в табл. 2.

При оптимизации выбора связей нейронов необходимо стремиться к минимизации среднего геометрического вероятностей ошибок первого и второго рода G ( P_EE ) (данные из табл. 1). Одновременно необходимо минимизировать среднее значение модулей корреляционных входных связей E (| corr |) (данные из табл. 2). Балансировка двух данных факторов для нейронов с двумя входами выполняется следующим образом:

min

0.91 - G ( P EE ) ^2- E ⁽ c ^orrl + 1.09 - ^ ( P EE ) ^2-( Ecorr ⁾² "

Т а б л и ц а 2

T a b l e 2

Коэффициенты корреляции между парами рассматриваемых статистических критериев The coefficients of correlation between pairs of statistical criteria under consideration

XI
----------►

	χ 2	ad 2	adL	sg	sgd	ω 2	ω 2 c	su 2
χ 2	1	0,423	0,672	0,037	–0,042	0,559	0,401	–0,726
ad 2	0,423	1	0,644	0,018	–0,145	0,226	0,393	–0,113
adL	0,672	0,644	1	0,056	0,209	0,827	0,832	–0,917
sg	0,037	0,018	0,056	1	0,132	0,414	0,402	–0,212
sgd	–0,042	–0,145	0,209	0,132	1	–0,242	–0,142	–0,041
ω 2	0,559	0,226	0,827	0,414	–0,242	1	0,885	–0,667
ω 2 c	0,401	0,393	0,832	0,402	–0,142	0,885	1	–0,764
su 2	–0,726	–0,113	–0,917	–0,212	–0,041	–0,667	–0,764	1

Р и с. 5. Обобщение большого числа статистических критериев многослойной сетью искусственных нейронов (аналогия с использованием глубоких нейронных сетей для распознавания лиц)

F i g. 5. Generalizing a large number of statistical criteria by a multilayered network of artificial neurons (analogy with the use of deep neural networks for face recognition)

Для нейронов с тремя входами связывание двух факторов описывается близким соотношением:

mJ 1-75 G ( P ee ) E ^{( )} + 0.25 G ( P ee )    ' E ⁽*"1 ”2 '

²                                     J .

При необходимости могут быть построены аналогичные соотношения для нейронов с любым числом входов.

Обсуждение и заключение

Следует отметить, что усилия сотен исследователей, развивавших математическую статистику в ХХ в., несопоставимы по размерам ресурсов, затраченных США, Канадой, Евросоюзом, Китаем, Россией на развитие технологий биометрической идентификации личности. С начала XXI в. совместными усилиями технологических лидеров в рамках международного комитета по стандартизации ISO/IEC JTC1 sc 37 (Биометрия) было создано и введено в действие порядка 120 международных стандартов; в стадии разработки находится около 30 стандартов. В России 44 из 120 международных стандартов гармонизованы и введены в действие. В настоящее время развиваются несколько технологий сканирования и обработки уникальных биометрических образов. Данные по биометрическим технологиям отражены в табл. 1.

После создания хи-квадрат критерия К. Пирсоном в 1900 г. его последователями было разработано несколько десятков подобных статистических критериев. Можно рассматривать весь ХХ в. как время синтеза новых статистических критериев. Видимо, в XXI в. тенденция синтеза новых статистических критериев продолжится, однако акценты развития статистической теории существенно изменятся. В данной статье мы показали, что эффективным является нейросетевое обобщение уже созданных критериев и критериев, которые еще будут разработаны. Существующих технологий обучения искусственных нейронных сетей вполне достаточно. В данном контексте крайне важным является создание новых статистических критериев, слабо коррелирующих с уже известными. Становится не столь важной относительная мощность нового статистического критерия; важнее то, как он дополняет другие критерии в нейросетевых обобщениях.

В рамках данной статьи мы показали, что нейросетевое объединение всего трех статистических критериев позволяет снизить ошибки первого и второго рода на 22 %. Предположительно, обобщение порядка 100 статистических критериев глубокой нейронной сетью позволит многократно снизить требования к размерам тестовых выборок. Вместо 200 опытов, необходимых сейчас, в ближайшем будущем будет достаточно выборки в 20 опытов.