Нейросетевой метод интерпретации флуктуаций электрических характеристик химических источников тока с целью контроля их внутреннего состояния

Системы контроля состояния химических источников тока (ХИТ) становятся неотъемлемой частью устройств и объектов ответственного применения. Наибольшую точность в определении параметров источников тока по анализу его характеристик in situ демонстрируют методы, основанные на обработке больших объемов данных - методы машинного обучения [1]. Тем не менее преимущества данных методов часто нивелируются недостаточным объемом обучающей выборки.

Рядом исследователей был предложен новый подход к анализу процессов в электрохимических системах: анализ нелинейностей и шумов напряжения [2-5]. Увеличение числа доступных для анализа параметров за счет глубокого анализа нелинейностей сигналов позволяет снизить необходимые объемы данных и повысить точность методов машинного обучения на небольших выборках. В свою очередь, как было продемонстрировано в работе [6], применение методов обучения к шумовым характеристикам источников тока позволяет значимо повысить точность существующих методов их интерпретации. В последние годы было предложено несколько техник анализа импеданса и шумовых характеристик источников тока, каждая из которых в отдельности повышает точность контроля состояния ХИТ: его пригодности для селективной сборки, степени деградации ( SoH) и степени заряжен-ности ( SoC). Тем не менее пока не была показана возможность объединения ряда таких техник в мультимодальный метод и не приведены примеры реализующих его архитектур.

Целью настоящей работы является создание нового нейросетевого метода интерпретации характеристик источников тока, интегрирующего ряд математических моделей, предложенных в предыдущих работах [6-8], в единый алгоритм. Разработанный алгоритм должен обеспечить мультимодальный контроль состояния ХИТ в процессе эксплуатации при сохранении или снижении требований к объему выборок данных за счет применения новых техник математического моделирования и машинного обучения. Необходимо провести валидацию предлагаемого метода на модельных и экспериментальных данных.

2.    Интерпретация флуктуаций электрических характеристик химического источника тока О f -^ Г ^ б)

-10

_12l---------------■--------------■---------------■--------------■■

Re{Z), mOhm а)

Рис. 1. Пример исследуемого сигнала: спектр импеданса (а) и шум напряжения литий-ионного ХИТ в процессе разряда постоянным током (б)

Приведем постановку задачи и описание метода. Исследуемыми сигналами являются сигналы напряжения ХИТ U (t) под воздействием внешней нагрузки I(t) и спектры импеданса ХИТ Z (f ), г де t - время, f - частота. Задана начальная (номинальная) ёмкость элемента С. Рассматривается кусочно-постоянная или квазипостоянная нагрузка I (t ) ^ 1C, в процессе которой фиксируются разрядные кривые U(t) и при помощи методики удаления тренда D(U) выделяются шумовые характеристики u(t), и синусоидальная нагрузка I (f )

с набором частот fi , при которой измеряется комплексное сопротивление Z(f ). Примеры исследуемых сигналов: годографа импеданса Z и шумов напряжения и приведены на рис. 1.

Проведение измерений экспериментальных параметров

Измерение напряжения U

Измерение импеданса Z

/Предваршельная обработка экспериментальных

^ Детре ндиро вание 5 (удаление постоянное составляющей у напряжения) %

данных

Удаление высокочастотной части импеданса.

Анализ шумов напряжения

Анализ спектров импеданса

Автокорреляционны й анализ

Применение модени-явтокодпровщпкадчя сортировки элементов по спектру электрохимического импеданса

Спектральный анализ

Обучение сети-автокодировщика

Статистический анализ

Г   Снижение размерностиспектров   5

I______________ импеданса ______________J

Агломсративная кластеризация внутренних представлений

^    - ~

Формирование наборов данных

Моделирование флуктуаций напряжения

Пред-об учение сети дискриминатора

Обучение генеративно-состязательной

__________ нейронной сети __________

Генерацпя наборов синтетических данных

Анализ сгенерированных данных

Тренировочный сет

Валидашюнный сет

Обучение глубокой нейронной сети

Предсказание параметров ХИТ

Анализ ошибки предсказания

Рис. 2. Блок-схема алгоритма, реализующего нейросетевой метод интерпретации шумовых характеристик ХИТ

При разбиении сигналов на отрезки для анализа, их длины подбираются так, чтобы статистические и спектральные характеристики шумовых характеристик были квазиста-ционарны при нестационарностях в исходных данных. Целевыми параметрами являются степень заряженности ХИТ ( SoC) и его класс по степени деградации (SoH):

SoC = ^£(£1 • 100%, grated

SoH = ^ax • 100%, (2) grated где Qc(t) - количество запасенной энергии в момент времени t, Qmax - максималвное запасаемое количество электричества, Qrated = С - номиналвная ёмкоств элемента.

Литий-ионные аккумуляторы типично признаются непригодными для работы при падении SoH до 60%, поэтому исследуемые ХИТ можно разделитв на два класса: работоспособные с SoH 100% — 70% и близкие к отказу при SoH 69% — 61%. Таким образом, задачу мулвтимодалвной обработки данных источника тока можно свести к определению класса ХИТ на основе импеданса элемента и определению SoC на основе данных шумов напряжения системы, включающей ХИТ.

Для предсказания данных целевых параметров используются методы машинного обучения: в процессе обучения проходит итерационный поиск набора параметров в («весов»), дающих минимум ошибки L математической модели N (в,ж) («нейронной сети») на некоторой подвыборке генеральной совокупности рассматриваемых сигналов {ж} [9]. Точность метода оценивается на тестовой подвыборке, не пересекающейся с использованной в обучении.

Блок-схема алгоритма, реализующего предложенный метод, приведена на рис. 2. Для определения класса ХИТ используется агломеративная кластеризация после снижения размерности спектров импеданса при помощи сети автокодировщика. Данные от ХИТ с общим классом включаются в выборку для обучения глубокой нейронной сети для оценки SoC и генеративно-состязательной сети. После аугментации выборки синтетическими данными от генеративно-состязательной сети происходит дообучение глубокой нейронной сети и предсказание SoC. Обучение и валидация производятся на данных, полученных в работе [6], и опубликованных наборах данных о циклировании литий-ионных аккумуляторов [10].

3.    Детрендирование сигнала напряжения

Первым этапом в анализе стохастических процессов является удаление из экспериментальных данных детерминированных компонент или тренда - так называемое «детрендирование» сигнала D(U ) = u + e ( U ), г де и - малая случайная составляющая, e ( U ) - ошибка методики детрендирования. Частью предлагаемого метода является методика детрендиро-вания сигнала на основе вариационной декомпозиции, впервые предложенная в работе [6]: разложение сигнала U на сумму узкополосных функций k U k и к с набором центральных частот f k- выбранных для минимизации обобщенного Лагранжиана. L(u k , f k ) [11] ^п фильтрация полученных узкополосных функций перед суммированием и восстановлением:

U (t) = Yu* (t),                                    (3)

k

u(t) = Yu k (t) • e — ^ , k

(D

где t - время, ^ k ^- набор показателей экспоненциального фильтра.

Данная методика требует валидации на модельных данных с заранее известным уровнем целевых шумов. Для моделирования тренда напряжения предлагается использовать формулу на основе использованной в работе [12], учитывающую экспоненциальные зависимости разрядно-зарядной кривой:

U = Uo — К •

Q (Q — it)

• it — К •

Q (Q — it)

• i„,j + A • exp(—B • it),

где Uo - начальное напряжение, Uo = 4.2 В, К - коэффициент амплитуды гиперболической части, Q - ёмкость, i - ток батареи, i_H4 - квазипостоянная (низкочастотная) составляющая нагрузки (i_H4 > 0 при разряде), t - время, A - коэффициент амплитуды экспоненциальной части, B - коэффициент наклона экспоненциальной части.

Для моделирования наложенного на тренд шума и использовались известные эмпирические и теоретические закономерности [2-5, 13]. Ещё в первых работах, посвященных моделированию шумовых характеристик источников тока [14], модели шумов были основаны на эквивалентных цепях замещения, описывающих поведение флуктуаций через взаимодействие генератора белого шума с комплексным сопротивлением Z. Так, на высоких частотах шумы источников тока можно считать тепловыми шумами [5], чья спектральная плотность мощности связана с действительной частью импеданса ХИТ Z(f ) по известной формуле Найквиста:

<* »           -к ^f     '^{Re(Z (f} »’

где h = 6.626 • 10^-34 Дж -с - постоя иная Планка, к = 1.38 • 10^-23 Дж/К - постоянная Больцмана, Т - температура элемента.

В низкочастотных диапазонах главной составляющей шумов напряжения является фликкер-шум Uf [5], т.е. цветной шум и_с с коэффициентом степенной зависимости от частоты у ~ —1, представимый как сумма шумовых процессов с распределением Коши -Лоренца [15]. Одной из моделей описания такого шума являются колебания сопротивления источника тока 5R при внешней нагрузке I:

u_f = I -(R_o + 6R)

В работе [13] продемонстрировано, что при постоянном уровне заряда шумы источника тока имеют распределение, близкое к нормальному. В свою очередь в работах [2, 5] получено, что среднеквадратическое отклонение шумов ХИТ растёт в начале и в конце процесса разряда. Поэтому для моделирования наложенного на тренд (5) целевого шума u(t) предлагается использовать случайный сигнал u_m(t), состоящий из суммы нестационарного нормально распределенного шума со среднеквадратическим отклонением, изменяющимся по параболическому закону в зависимости от времени (что имитирует динамику шума в работе [2]), и шума с распределением Коши.

Для учета зависимостей спектральных характеристик шума от Z источника тока, отмеченных в (6) - (7), комплексный спектр F_m шума и_т предлагается модифицировать действительной частью импеданса Re (Z(f )) литий-ионного аккумулятора цилиндрического типа 18 650 из набора данных [12], дополненной симметрично для отрицательных частот для получения двустороннего спектра:

u(t)= ift(F m -Re(Z (f ))),

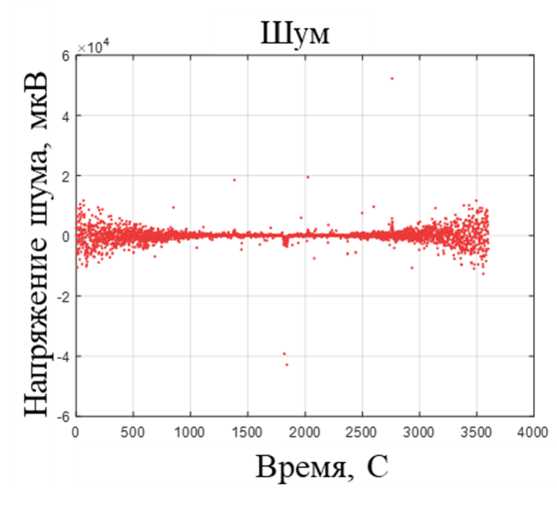
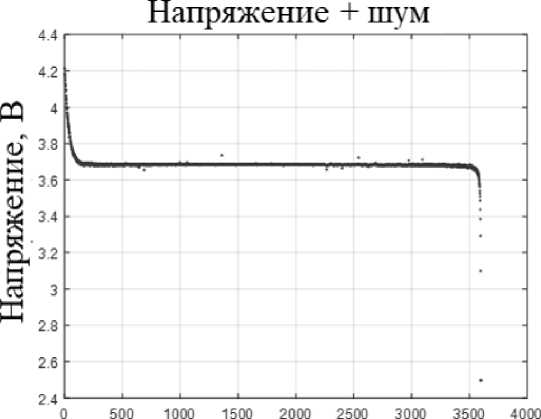
где ift(y) - обратное преобразование Фурье последовательности у, F_m - фурье-спектр сигнала и_т, f - частота. Умножение спектра Фурье в комплексном виде позволяет сохранить фазу и восстановить действительный сигнал при помощи обратного преобразования Фурье. Пример полученного модельного шума и разрядной кривой приведен на рис. 3.

Для сравнения с предлагаемой методикой были выбраны следующие методики, применяемые для анализа шумов напряжения источников тока: 1) детрендирование полиномом степени п = 10 [4]; 2) детрендирование скользящим средним по 200 точкам сигнала, как предложено в работах [2,3]. Результаты применения сравниваемых методов детрендирова-ния к модельному сигналу приведены на рис. 4.

Для сравнения результатов детрендирования использовался корень среднеквадратичной ошибки RMSE, определяемый в общем виде как:

I Ею 1/И^ — ^И²

RMSE = W ±Д1=ДД_--- ,

где А - целевые значения, Y - результат работы алгоритма, N - длина сигнала.

а)

Рис. 3. Модельные шумовые характеристики (а) и разрядные кривые (б)

Время, с

б)

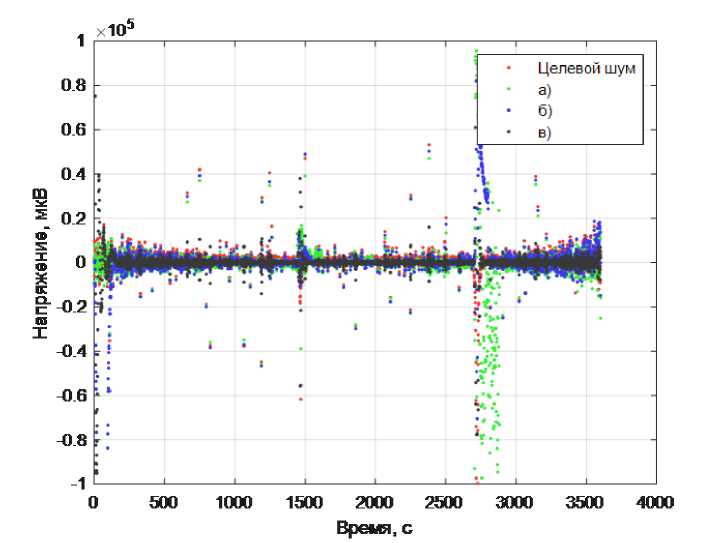
Рис. 4. Результаты детрендирования с разбиением сигнала на N = 20 равных фрагментов: а) при помощи удаления полиномиального тренда; б) при помощи скользящего среднего; в) при помощи метода на основе вариационной декомпозиции

Для предложенного метода RMSE vmd = 0.0013, что более чем в 10 раз ниже корня среднеквадратичной ошибки для методов детрендирования полиномом (RMSE p _O i = 0.0162) и более чем в 4 раза ниже, чем при детрендировании скользящим средним ( RMSE v^g. = 0.0072).

Отдельно стоит отметить преимущество методики при наличии резких перепадов амплитуды шумов в сигнале (таких, как в районе 2600 с на рис. 4), характерных для шумов с распределением по Коши. Как видно из рис. 4, такие перепады значений в сигнале приводят к искажениям и высокой ошибке детрендирования (3) при удалении тренда скользящим средним или полиномиальной зависимостью. При этом сигнал, детрендированный при помощи метода на основе вариационной декомпозиции, имеет меньшее отклонение от целевого в области резкого изменения амплитуды целевого шума. Данное преимущество делает рассматриваемую методику детрендирования предпочтительной для применения при работе с разрядными кривыми с нагрузкой около 1С, в которых могут встречаться резкие изменения значений тренда напряжения и дисперсии шумов.

4.    Блок автокодировщика для анализа импеданса ХИТ

Поскольку спектральная плотность мощности шумов напряжения ХИТ связана со спектром его электрохимического импеданса, особенности комплексного сопротивления элементов могут служить индикатором отличия шумовых характеристик аккумуляторов. Проведение сортировки элементов по спектрам их импеданса позволит оптимизировать процесс постановки экспериментов и составления датасетов как часть мультимодального метода контроля и избежать неисправностей в процессе эксплуатации аккумуляторов.

Спектры импеданса литий-ионных источников тока описываются десятками или даже сотнями точек в широком частотном диапазоне от десятков кГц до единиц мГц. В силу сложности определения физически обоснованной метрики сравнения двух элементов в многомерном пространстве и высокой вычислительной сложности задач типа селективной сборки рационально снизить размерность сигнала. Целевую размерность можно определить из числа параметров, необходимых для описания модели эквивалентной цепи источника тока: порядка 10 параметров (размерность [10; 1]).

Пространственное представление спектра импеданса ХИТ и наличие в нем локальных особенностей позволяет эффективно применять для его обработки свёрточные архитектуры нейронных сетей, в которых сигнал сжимается серией последовательно примененных локальных фильтров [16]. В то же время ряд работ [17, 18] указывает на то, что для обработки сигналов источников тока с иерархией данных рационально использовать рекуррентные слои, такие как слои с долгой краткосрочной памятью (LSTM). Разработанная архитектура, представленная на рис. 5, включает в себя сверточные слои, слои LSTM и слои max pooling.

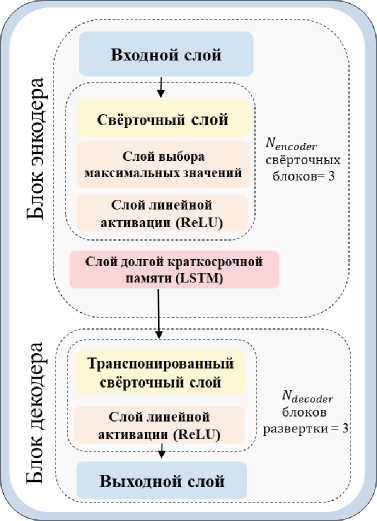
Рис. 5. Архитектура нейронной сети-автокодировщика для обработки импеданса химических источников тока

Для валидации алгоритма на открытых данных был использован набор данных NASA AMES prognostics dataset с информацией об импедансе аккумуляторов при максимальном уровне ёмкости от 95 до 60% от номинальной. После обучения в течение 50000 эпох с размером пакета данных 128 сигналов автокодировщик восстанавливает спектры импеданса из сжатого представления с корнем среднеквадратичной ошибки 8.6 мкОм на точку спектра (ошибка рассчитывается по формуле (9)). Пример восстановленных и реальных спектров импеданса приведен на рис. 6. Видно, что восстановленный из сжатого представления спектр импеданса сохраняет основные зависимости входного сигнала: полукруглую форму годографа импеданса с действительной частью комплексного сопротивления 35...80 Ом, что служит качественным подтверждением верности избранной модели автокодировщика.

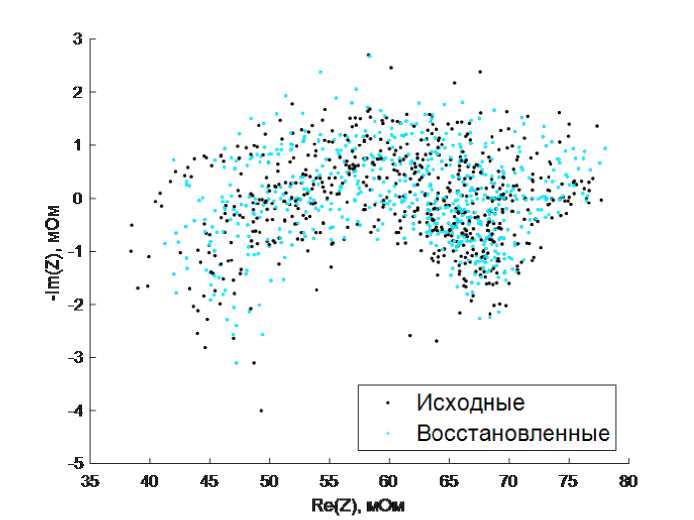
Рис. 6. Восстановленные (обозначены голубыми точками) и исходные (обозначены черным) данные импеданса из тестовой выборки

Для классификации ХИТ внутренние представления импедансов были сгруппированы при помощи агломеративной кластеризации с использованием расстояний Фреше [19]. Результаты разделения сигналов на два кластера представлены на рис. 7. При кластеризации внутренних представлений вместо полных импедансов точность разделения аккумуляторов с SoH >= 71% и SoH <  71% возрастает с 84% до 90%, что делает данный метод применимым для отбраковки аккумуляторов перед использованием.

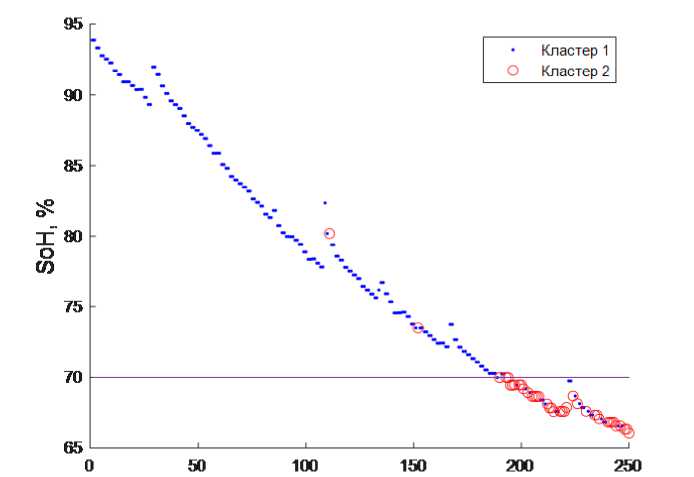
№ измерения Импеданса

Рис. 7. Результаты кластеризации спектров импеданса после снижения размерности сигнала

5.    Блок генеративно-состязательной нейронной сети для моделирования шумов напряжения

Увеличить преимущества метода анализа шумовых характеристик может применение порождающих моделей машинного обучения, которые позволяли бы расширять наборы данных без проведения дополнительных экспериментов. Для генерации стохастических сигналов напряжения используется модель шумовых характеристик источников тока, основанная на применении генеративно-состязательной нейронной сети (так называемой GAN -generative adversarial network). Генеративно-состязательная нейронная сеть (GAN) состоит из двух блоков: генератора G и дискриминатора D [20]. Сеть-генератор обучается создавать синтетические данные, неотличимые от реальных, а сеть-дискриминатор - отличать сгенерированные данные от экспериментальных.

На вход сети генератора подается случайный сигнал £ с нормальным распределением |21] :

1         €2

Р (£) = N (0,1) = -= е^- т .                          (10)

• V 2я

В процессе работы генератор решает задачу регрессии; возвращаемые значения и_д = и_д (£) совпадают по размерности с реальными данными и_г.

Сгенерированные данные и_д и реальные сигналы и_г подаются на вход дискриминатора. Для классификации данных в дискриминаторе используется сигмоидальная функция:

<Аи) =          тг,

• ^{k У} 1 + _e~y_d ( и )

где у а (и) - некоторая функция отклика сети на сигнал и. Блок-схема архитектуры сети дискриминатора приведена на рис. 8. В её основе лежат свёрточные и LSTM слои. Подобная архитектура с суммированием выходов параллельных слоёв, показала свою эффективность ^в [6]-

Синтетические данные

Реальные данные

Input layer

Входной слой

Convolution layer

Свёрточный слой

Leaky ReLU layer

Слой нелинейной активации

Convolution layer

Свёрточный слой

Convolution layer

Свёрточный слой

LSTM layer

Слой долгой краткосрочной памяти

LSTM layer

Слой долгой краткосрочной памяти

LSTM layer

Слой долгой краткосрочной памяти

Leaky ReLU layer

Слой нелинейной активации

Leaky ReLU layer

Слой нелинейной активации

Leaky ReLU layer

Слой нелинейной активации

Max pooling layer

Слой выбора наибольших значений

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Fully connected layer

Полносвязный слой

Addition layer

Слой суммирования для усреднения

Output layer

Выходной слой

Класс данных

Рис. 8. Блок-схема архитектуры сети дискриминатора

До обучения в связке с генератором, дискриминатор был предобучен различать реальные данные и гауссов шум с равной реальной дисперсией до достижения точности в 90%. В процессе обучения GAN-архитектуры дискриминатор случайным образом обучался от

0 до 2 раз за шаг обучения, чтобы снизить шансы вырождения множества синтетических сигналов.

В основу архитектуры блока генератора были положены слои транспонированной свёртки и LSTM слои. Для того чтобы избежать вырождения сигналов, был сделан выбор в пользу слоёв тангенциальной активации вместо полулинейной. Блок-схема архитектуры генератора приведена на рис. 9.

Случайные данные

Random input layer

Входной слой

Hyperbolic tangent

Слой тангенциальной активации

Hyperbolic tangent

Слой тангенциальной активации

Transposed Convolution layer

Transposed Convolution layer

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Addition layer

Слой суммирования для усреднения

Batch normalization layer Слой пакетной нормализации

Hyperbolic tangent х2/

Слой тангенциальной активации

Fully connected layer

Полносвязный слой

Output layer

Выходной слой

Синтетические данные

Рис. 9. Блок-схема архитектуры сети генератора

После обучения в течение 1000 эпох данная модель способна порождать синтетические данные, имеющие большее сходство с реальными сигналами на участках разрядной кривой с перепадом SoC не более 2%, чем гауссов шум с теми же средним и дисперсией (среднее косинусное расстояние между сигналами 0.8101 против 0.7623). Примеры сгенерированных сигналов приведены на рис. 10.

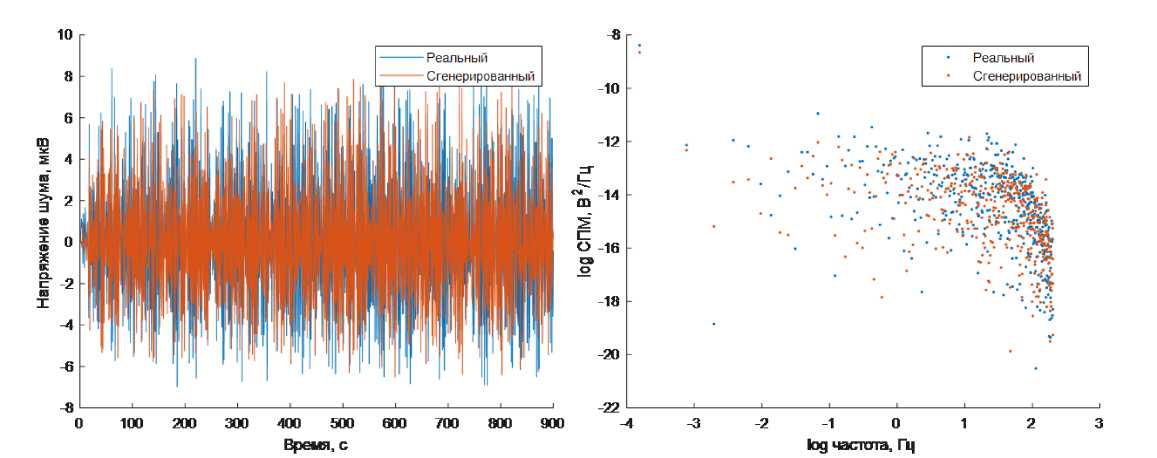
а)                                                      б)

Рис. 10. а) Сравнение сгенерированных и полученные экспериментально флуктуации напряжения; б) Спектральная характеристика сгенерированных и полученных экспериментально флуктуации напряжения (SoC = 76%)

6.    Нейронная сеть для определения степени заряженности ХИТ

Для разметки синтетических данных проводится обучение нейронной LSTM-сети на наборе данных о шумах напряжения. Блок-схема архитектуры сети представлена на рис. 11 и совпадает с предложенной в работе [6].

Сигнал

Input layer

Входной слой

LSTM layer

Слой долгой краткосрочной памяти

LSTM layer

LSTM layer

Слой долгой краткосрочной памяти Слой долгой краткосрочной памяти

LSTM layer

Слой долгой краткосрочной памяти

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Dropout

Слой, с заданной вероятностью обращающий в 0 компоненты выхода

Hyperbolic tangent

Слой тангенциальной активации

Hyperbolic tangent

Слой тангенциальной активации

Hyperbolic tangent

Слой тангенциальной активации

Hyperbolic tangent

Слой тангенциальной активации

----Л—

Addition layer

Слой суммирования для усреднения

Fully connected layer

Полносвязный слой

Regression layer Выходной слой регрессии

SoC

Рис. 11. Блок-схема архитектуры нейронной сети для решения задачи регрессии

С помощью нейронной сети для каждого из сгенерированных сигналов решается задача регрессии: шуму напряжения сопоставляется уровень заряда аккумулятора SoC. Как можно судить по распределению сгенерированных сигналов по степени заряженности, представленному на рис. 11, для применения предложенной порождающей модели необходимо, чтобы не менее половины входящих в обучающую выборку экспериментальных данных принадлежала области 0 — 50% SoC.

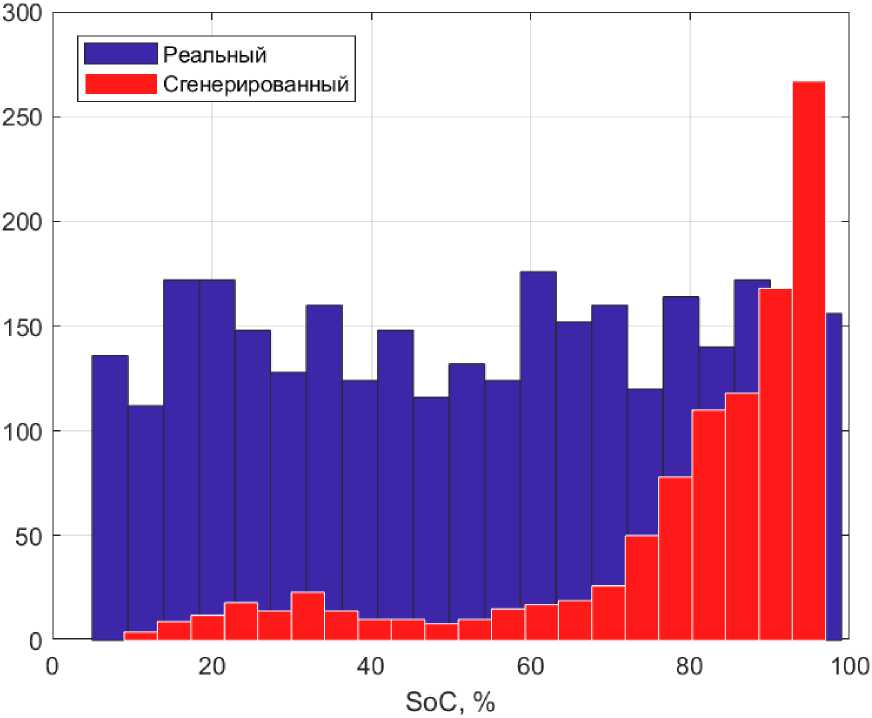
Рис. 12. Распределение сгенерированных данных и _д (красным) по степени заряженности (SoC) среди 1000 сгенерированных сигналов в сравнении с распределением реальных сигналов и _г (синим) из обучающей выборки по степени заряженности

Многократно повторяя генерацию сигнала и отбирая при помощи нейронной сети классификатора сигналы с требуемым SoC возможно синтезировать шумовые характеристики источников тока на протяжении всего разряда. К данным о шумах добавляются данные о разрядных кривых для соответствующего SoC и полученные данные исполвзуются для аугментации набора экспериментальных данных.

После аугментации сигнала возможно провести повторное обучение глубокой нейронной сети. Было подтверждено, что данная операция повышает точность определения SoC. Так, после двукратного увеличения общего числа сигналов в обучающей выборке удалось увеличить точность определения SoC на тестовом наборе реальных данных до 4.9%. Сравнение точности предложенного метода с методом определения наклона спектральной плотности мощности (СПМ) шумов и методом измерения напряжения [22] приведено на рис. 13. Сравнение проведено на примере нескольких циклов разряда литий-ионного аккумулятора Энергия ЛИЦ 18650 ICR 19/66 для сигналов длиной 900 точек с частотой дискретизации 20 Гц.

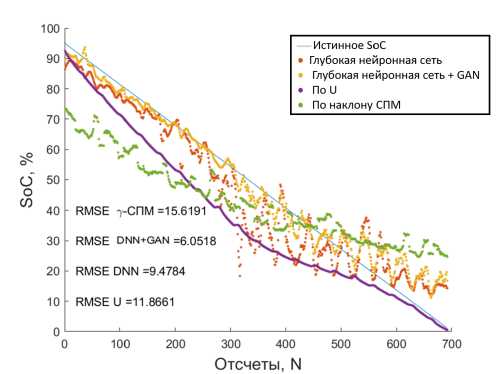
а)

Рис. 13. Результаты расчёта SoC аккумулятора ЛИЦ 18650 ICR 19/66: а) при разряде серией разрядных импульсов 1С, температура поверхности аккумулятора 45o С; б) при разряде постоянным током 1С, температура поверхности аккумулятора 25o С (GAN - генеративно-состязательная нейронная сеть)

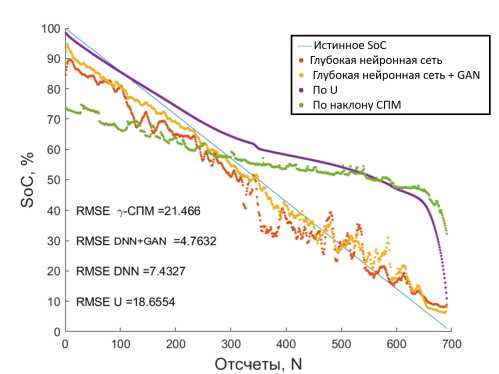
б)

Видно, что для исследуемых разрядных кривых ошибка определения SoC снизилась более чем на 3.4% после аугментации данных. При этом удалось добиться снижения ошибки определения SoC при разряде АБ не только постоянным током, но и сериями разрядных импульсов. Видно, что предложенный метод обеспечивает меньшее рассогласование экспериментального SoC с предсказанным, чем предлагаемый ранее метод на основе глубокой нейронной сети [6] при тех же параметрах входного сигнала, при этом выигрыш по точности составляет в среднем 31 % при использовании метрики RMSE (9).

7.    Заключение

Предложен нейросетевой метод интерпретации флуктуаций электрических характеристик источников тока для контроля внутреннего состояния аккумуляторов. Данный мультимодальный метод основан на последовательном применении ряда техник машинного обучения к сигналу напряжения ХИТ и может быть логически разделен на несколько этапов: удаление тренда сигнала, анализ отклика элемента на синусоидальный ток (анализ спектра импеданса ХИТ), обучение генеративно-состязательной нейронной сети и расширение объема данных, обучение глубокой нейронной сети для решения задачи регрессии.

На модельных данных показано, что методика удаления тренда на основе вариационной декомпозиции обеспечивает до 10 раз ниже ошибку разделения шума и детерминированной компоненты, чем детрендирование полиномом или скользящим средним.

Показано, как кластеризация внутренних представлений спектров импеданса позволяет по простому критерию отбраковывать элементы с низкой максимальной ёмкостью, снижая риски при эксплуатации ХИТ и повышая однородность экспериментальных данных.

Применение генеративно-состязательной архитектуры позволяет повысить точность методов глубокого обучения и снизить требования к размерам датасетов и объем проводимых испытаний за счет аугментации. Результаты валидации показывают, что интерпретация шумов напряжения при помощи глубокой нейронной сети позволяет проводить контроль состояния коммерческих литий-ионных аккумуляторов со среднеквадратичной ошибкой (RMSE], равной 4.9% на тестовой выборке при разной температуре и различных видах токовой нагрузки.