Нейросетевой метод семантического вероятностного вывода в задаче улучшения релевантности результатов поискового запроса

Введение. Область исследования информационного поиска (ИП) широко освещена в русскоязычной и зарубежной литературе, о чем свидетельствуют многочисленные монографии и статьи. Термин „информационный поиск“ был предложен Кельвином Муэр-сом в 1948 г. в его докторской диссертации, опубликован и употребляется в литературе с 1950 г. [1]. Центральным понятием ИП является характеристика релевантности — явно заданная величина, характеризующая пару документ-запрос, другими словами, насколько документ отвечает условиям запроса. Традиционно в моделях оценки релевантности используется статистический подход, который уже развивается более 30 лет. Наиболее значимыми трудами в данной области являются [2], [3], [4], [5], [6], [7], [8]. Первоначально область применения данных алгоритмов была ограничена библиотечным делом для наиболее быстрого и качественного поиска научной литературы. Широкое распространение ИП получил с появлением Интернета.

Важной частью ИП являются алгоритмы полнотекстового поиска. Существует целое семейство функций для формирования результирующей выборки по текстовому запросу. Во многих прикладных системах реализован алгоритм ВМ25 [9], [10]. Рассмотрим его подробнее. ВМ25 — это семейство поисковых функций на неупорядоченном множестве слов, так называемом „мешке слов¹¹, и множестве документов. Алгоритм оценивает каждый документ из набора на основе частот встречаемости слов запроса, без учета близости между словами. Одна из распространенных форм этой функции описана ниже. Пусть дан запрос Q, содержащий слова qi...q_Tl, тогда функция ВМ25 дает следующую оценку релевантности документа D запросу Q:

s(D,Q) = ^IDF^ ?=i

f^D^k + l) f(qvDHKl-b + b^y

где J(q^D) — частота слова q; в документе D (следует отметить, что частоту слова можно также рассчитывать относительно группы документов, объеденных некоторым общим свойством), \D\ есть длина документа, <  \D\ >  — средняя длина документа, к и b — свободные коэффициенты.

Таким образом, оценка релевантности документа D подсчитывается на основе частот встречаемости каждого слова q.^ причем в топ выдачи попадают документы с более специ-ализироваными, характерными словами. Информация, определенная в работе Шеннона, в контексте информационного поиска трудно измерима [11]. Оценки эффективности поисковой функции могут быть выполнены на основе двух характеристик, а именно точности и полноты, соответственно, точность определим следующим образом:

| D_rei П D_retr | I Dretr |

где DTei — множество релевантных документов в выдаче, a DTetT — множество документов, найденных системой. Следует отметить, что приведенная выше оценка является не единственной, к примеру, она не учитывает порядок выдачи или степень релевантности того или иного документа.

Вероятностный семантический вывод. Принцип семантического вероятностного вывода заключается в обнаружении максимально специфичных условных связей между n.-граммами и документами. Информация, подаваемая на вход метода, кодируется одноместными предикатами Р‘(а) <—> (тфа) = хру ^гД^е ^(я) — информация, a Xjj — ее значения на текущем объекте а, он представляет собой текст и метаинформацию документа. Вывод происходит замыканием относительно бинарных операторов ->, A, V логики высказываний. Предикаты Pj^a) и -iF^a) являются литералами (атомарными высказываниями или их отрицаниями), которые будем обозначать как о,/3,7,... G L, где L — множество всех литералов в словаре Ру г = l,...,n;j = l,...,nt [12]. В процессе семантического вероятностного вывода алгоритм обнаруживает множество R правил (условных связей) вида:

R = (оу А ... A Qk => ЗУ Ш,..., а^ 3 Е L,

где «1, ..., а^ — входные предикаты, кодирующие вхождение n-грамм в текст. Правила характеризуются оценкой условной вероятности, которая вычисляется следующим образом.

Подсчитаем число случаев n(«i,..., ak, 33 когда произошло событие < сд,..., ak, 3 > — одновременное срабатывание < сд,..., ak >, иными словами, при З-^З- Далее подсчитаем случаи тг⁺(сд, ...,сд,/3) и тгДсд,..., аь, 33 раздельно при 3^3- Тогда оценка условной вероятности правила (1) равна:

(n^ai,...,afc,/^-пДа1,...,од,/3)) ^Мп,...,^ =------—------—------.           (4)

(71(01, ...,^-,/3))

Алгоритм стремится максимизировать эту оценку. Правило Ry = (оф..., а:^ => 7) будем называть более общим, чем правило R₂ = (ад,..., оф ^=> сЗ обозначим это как Ry С- R₂ тогда и только тогда, когда {а],..., аф} С {фу..., дф}Д1 < ^2, и не менее общим Ry A R^ если kl < /с2. Очевидно, что Ry A: R₂ = > Ry Е R₂ и Ry >- R₂ —> Ry H R₂, где A — доказуемость в исчислении высказываний. Таким образом, не менее общие (и более общие) высказывания логически сильнее. Кроме того, более общие правила проще, так как содержат меньшее число литералов в посылке правила [13].

Вероятностным законом будем называть такое правило R, которое нельзя логически усилить, не уменьшив его условную вероятность, т. е. если R 7- R, то p^R) < мЗ^З Вероятностные законы — это наиболее общие, простые и логически сильные правила среди правил, имеющих не более высокую условную вероятность. Обозначим множество всех вероятностных законов через PL. Отношение вероятностного вывода Ry С R₂, Ry, R₂ Е PL определим как одновременное выполнение двух неравенств Ry Р R₂ и p^Ry) <  рЗ^З Если оба неравенства строгие, то отношение вероятносного вывода будем называть строгим отношением вероятностного вывода Ry С R₂<=> Ry >- R₂ и p(Ry) < p(R₂3

Семантическим вероятностным выводом будем называть максимальную (которую нельзя продолжить) последовательность вероятностных законов, находящихся в отношении строгого вероятностного вывода Ry С R₂ □ ... □ Rk- Последний вероятностный закон Rk в этом выводе будет называться максимально специфичным. Показано, что классификация по максимально специфическим правилам непротиворечива [13].

Алгоритм уточнения запроса. Уточнение запроса выполняется на основании ручной классификации первичной выдачи документов пользователем. Естественно предположить, что человек выполнит построение уточняющего запроса более качественно после изучения выборки документов. В данном случае алгоритм дает преимущество во времени построения запроса, основываясь на том предположении, что психофизическое восприятие подсветки ключевых слов в документе позволит быстрее определить релевантность документа, нежели совершить два действия, а именно определить релевантность и выделить стоп-слова. На рис. 1 представлена блок-схема алгоритма уточнения. Точкой входа в алгоритм является выдача документов первичного запроса. Вторым шагом алгоритма является классификация документов пользователем, а именно указываются те документы, наподобие которых нужно исключить из выдачи. На основе этого шага генерируется предикат 3- Далее проводятся нормализация и взвешивание слов следующим образом, производятся стемминг и фильтрация стоп-слов, к которым относятся союзы, предлоги, междометия. Далее подсчитывается частота внутри класса документов, для которых выполняется /3, обозначим /(/3) и 33^33 Из набора термов исключаются все слова, для которых        < 3. На основании полученной выборки формируется которое может быть дополнено литералами метаинформации документа, к примеру, url-ом или датой публикации. После чего к полученному множеству литералов и документов применяется

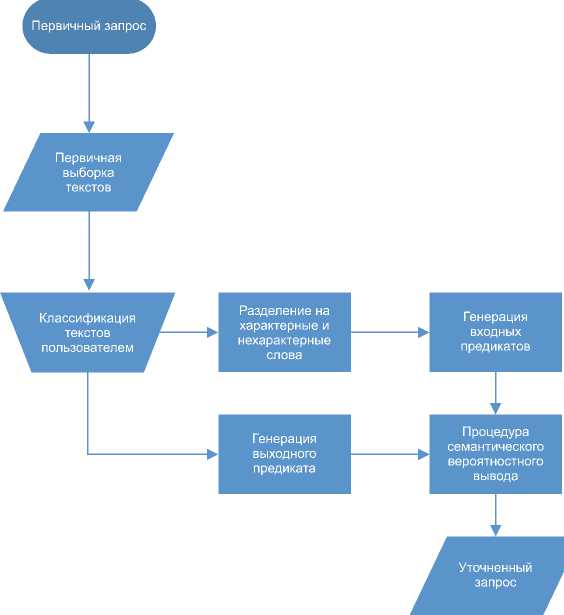
Рис. 1. Блок-схема, алгоритма, улучшения релевантности поиска.

описанная выше процедура семантического вероятностного вывода. На выходе алгоритм возвращает несколько рекомендуемых наборов стоп-слов. Алгоритм был протестирован на выборке текстов, собранных из Интернета, объем составляет 2317 текстов. В качестве первичного запроса использовалось слово „замок11. Целью было выделить тексты, посвященные теме „замков11, и отфильтровать тексты про „замки11. Результирующий запрос выглядит следующим образом: „замок — (новые король расположен Рейтинг)11. Уточненный запрос повысил точность с Р с 51,6% до 91,6%. Фраза „(новые король расположен Рейтинг)11 означает стоп-слова, т. е. в выдаче должны быть документы, в которых обязательно отсутствуют указанные слова.

Выводы. Таким образом, описанная выше модель является алгоритмом обучения с учителем, выявляет наиболее вероятные закономерности в данных в удобной для человека, форме, а именно на языке логики высказываний. В применении к задаче уточнения поискового запроса метод показал быструю сходимость и практическую значимость. Метод внедрен и проходит апробацию в информационно-аналитической системе AlemSemantics.