Нейросетевые методы оценки качества поверхностных вод по гидробиологическим показателям
Автор: Шитиков В.К., Зинченко Т.Д., Головатюк Л.В.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Биология и экология
Статья в выпуске: 2 т.4, 2002 года.
Бесплатный доступ
Представлен опыт использования искусственных нейронных сетей для моделирования стохастической связи показателей качества поверхностных вод со структурно-функциональными характеристиками донных сообществ. Приведены примеры обучения сетей различной конфигурации для оценки класса качества вод. Описан генетический алгоритм для выделения таксономических групп зообентоса, являющихся индикаторами состояния водоемов.
Короткий адрес: https://sciup.org/148197701
IDR: 148197701 | УДК: 577.4
Текст научной статьи Нейросетевые методы оценки качества поверхностных вод по гидробиологическим показателям
Анализ эффективности методов нейросетевого моделирования осуществлялся на массиве гидробиологических наблюдений [7], проведенных на 34 малых реках разного типа и степени антропогенной нагрузки, расположенных в степной и лесостепной зонах Самарской области. В обучающую выборку были включены 542 пробы, взятые на 247 станциях за период с 1987 по 2001 г.г. Для каждой станции наблюдения по совокупности гидрохимических показателей оценивали класс качества вод (Y) от 1 до 6 в соответствии с методиками [2, 3]. В качестве объектов биологического мониторинга в отобранных точках наблюдения использовались показатели обилия 546 видов организмов зообентоса. Суммарные значения численности Tsj и биомассы Bsj видов, принадлежащим к различным таксонам, пересчитывались в величины логарифма плотности населения хj = Ln((TsjBsj)0,5), которые использовались в качестве варьируемых переменных Хв, nв = 49. Для наиболее представительного семейства хиро-номид детализация таксономических групп была выполнена на уровне подсемейств и триб. Подпространство признаков Xи было сформировано из 9 широкоупотребляемых индексов и обобщенных показателей, рекомендуемых к применению [1]. Вычисления проводились с применением универсальной программы нейросетевого анализа STATISTICA Neural Networks (адрес в Интернете Neuralnetwork).
S - взвешенная сумма входных сигналов:
n
S = Х wx- T, i-I где T - порог нейрона;
F - функция активации нейрона, преобразующая взвешенную сумму в выходной сигнал У = F ( S ).
Вид функции активации F может иметь различное математическое выражение, из которых наиболее широкое распространение получили линейная y = k • S и логистичес кая у =
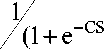
)
функции, где С >0 - ко- эффициент ширины сигмоидной кривой, имеющей S-образную форму.
В основе нейросетевого подхода [10] лежит идея построения вычислительного устройства из большого числа параллельно работающих простых элементов (т.е. описанных выше формальных нейронов), которые функ-
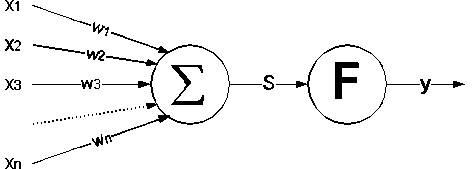
Рис.1. Структура искусственного нейрона ционируют независимо друг от друга и связаны между собой однонаправленными каналами передачи информации. Каждый отдельный нейрон моделируется довольно простой функцией, но зато совокупная сложность модели, гибкость ее функционирования и другие важнейшие качества определяются структурой связей и многоуровневой иерархией всей сети.
На сегодня описано много разновидностей нейронных сетей [10-13], характерных для различных типов задач. Рассмотрим возможности обучения ИНС на примере трехслойного персептрона [11] с прямым распространением информации, представленного на рис.2 и моделирующего альтернативное значение отклика Y.
Нейроны регулярным образом организованы в слои, причем элементы любого слоя связаны только с нейронами предыдущего слоя, т.е. информация распространяется от предыдущих слоёв к последующим. Во входной (распределительный) слой сети подаются значения обилия 27 таксономических групп зообентоса, отобранных в результате генетического алгоритма, а также количество видов в пробе. Взвешенные линейные комбинации функций преобразования элементов промежуточного слоя, состоящие из 14 ассоциативных нейронов, составляют реакцию системы. На выходе обученной нами сети формируется логическое высказывание "Чисто" (класс качества вод I-III) или "Грязно" (классы качества вод- IV-VI) в виде некоторого значения апостериорной вероятности на интервале от 0 до 1. Эффективность синтезируемой ИНС зависит от многих структурных и вычислительных факторов, которые обычно подбираются полуэмпирическим путем:
-
- количества промежуточных слоев и числа элементов в каждом слое;
-
- математического выражения для функции активации нейронов каждого слоя;
-
- используемого алгоритма и критерия оптимизации ошибки при обучении сети;
-
- соотношения между обучающей и контрольной выборками для независимой кросспроверки качества сети.
Наилучшая сеть, конфигурация которой представлена на рис.2, была обучена методом оптимизации Левенберга-Маркара с оценкой качества ИНС по информационному критерия (простой энтропии). Вариант построения нелинейной разделяющей поверхности с использованием сигмоидной функции активации оказался более эффективен по сравнению с вариантом линейных разделяющих гиперплоскостей. Сеть обучалась на 400 примерах, а остальные 120 примеров выделялись в качестве внешнего дополнения и независимого контроля качества сети. Результаты моделирования, представленные в табл.2, по традиции для всех задач классификации оценивались как доли ошибочных

Рис.2. Схема многослойного персептрона для оценки категории качества воды по обилию групп зообентоса
Таблица 2. Результаты использования модели персептрона с одним промежуточным слоем для оценки категории качества воды
|
Результат прогноза |
Обучающая выборка |
Контрольное множество |
||||
|
Класс “Чисто” |
Класс “Грязно” |
Правильный прогноз, % |
Класс “Чисто” |
Класс “Грязно” |
Правильный прогноз, % |
|
|
“Чисто” |
141 |
0 |
97,9 |
34 |
4 |
91,9 |
|
“Грязно” |
2 |
276 |
100 |
2 |
58 |
92,1 |
|
Отказ |
1 |
0 |
1 |
1 |
||
|
Итого |
144 |
276 |
99,3 |
37 |
63 |
92,0 |
опознаний на обеих выборках.
Решение задачи классификации с многими классами
Другим примером нейронной сети для непосредственной оценки значения класса качества водоемов в виде числа от 1 до 6 является персептрон с одним промежуточным слоем, архитектура которого представлена на рис.3. В качестве девяти варьируемых переменных было использовано подмножество обобщенных гидробиологических показателей Хи. Сеть имеет 5 выходов, соответствующие каждому из присутствующих в обучающей выборке классов качества воды и при правильном распознавании на одном из выходных элементов появляется высокое значение активации при незначительной ее величине на остальных четырех. Нами использовалась в выходном слое специальная функция активации (Softmax), представляющая собой взвешенную и нормированную на еди- ницу сумму экспонент. Нетрудно показать, что если входные данные представляют собой выборку из какого-либо экспоненциального распределения, то выходы софтмакс-эле-ментов можно трактовать как вероятности. Например, если для измерения на ст.1 р. Бай-туган активации выходных нейронов сети оказались равными {0,314; 0,503; 0,142; 0,028; 0,018}, то с вероятностью 0,503 можно предположить, что это измерение было взято из водоема 3 класса качества, а с вероятностью 0,817 ‒ из водоема 2-3 классов.
Результаты достоверности оценки классов качества представим в виде таблицы сопряженности "Факт-Прогноз" (табл.3), где по главной диагонали проставлены частоты правильной оценки групп измерений, а в остальных клетках ‒ имеющиеся ошибки прогноза отдельно для обучающей выборки и контрольной последовательности.
Нейронную сеть, вследствие ее принципиальной многомерности, обычно интерпре-
Число видов в пробе
Обшаячисленность
Общая биомасса
Доля хищников (по численности)
Доля хищников (по биомассе) Индекс Шеннона
Индекс Вудивисса
Индекс Пареле
ИндексБалушкиной
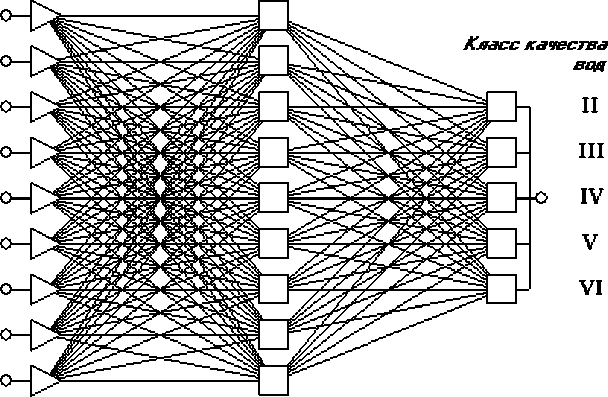
Рис.3. Нейронная сеть для прогнозирования пяти классов качества воды
Таблица 3. Результаты прогнозирования класса качества вод по модели многослойного персептрона
Решение задачи о понижении размерности
Задача состоит в получении сжатого (редуцированного) представления исходных данных в виде матрицы F с меньшим числом переменных p (n > p) без существенной потери информации, содержащейся в исходной матрице X. Один из недостатков традиционного факторного анализа заключается в ортогональном характере преобразований, в результате чего улавливаются только линейные направления максимальной вариации. Более общий нелинейный вариант метода главных компонент основан на применении автоассоциативных сетей [14, 15]. Такая симметричная сеть предназначена для воспроизведения на выходе своих же сигналов, т.е. число выходов совпадает с числом входов, а все нейроны имеют особое свойство. Если число элементов промежуточного слоя сделать меньше числа входов/выходов, то это заставляет сеть "сжимать" информацию, представляя ее меньшим числом переменных. Трехслойная автоассоциативная сеть
Таблица 4. Анализ чувствительности входных переменных модели многослойного персептрона для прогнозирования класса качества вод
Чтобы осуществить нелинейное понижение размерности исходной матрицы наблюдений для прогнозирования класса качества вод, используемой в предыдущем примере, выполняли следующие действия:
-
- построили и обучили на множестве из
520 примеров автоассоциативную сеть ‒ персептрон с пятью слоями;
-
- удалили два последних слоя автоассо-циативной сети и получили сеть для пре-процессирования, понижающую размерность данных, где количество варьируемых признаков было сведено от 9 до 3 без существенной потери информации;
-
- строили обрабатывающую сеть в виде второго трехслойного персептрона (при обучении на ее вход подавали выходные сигналы пре-процессирующей сети);
-
- объединив обе сети (см. рис.4), получили единую сеть, которая последовательно пересчитывает исходные данные в пространство трех главных компонент, после чего обрабатывает уже преобразованные факторы,
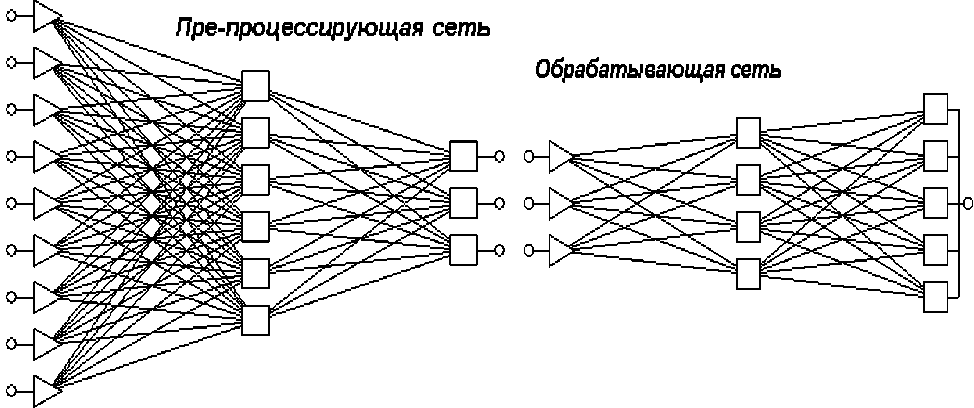
Рис.4. Последовательность двух сетей для понижения размерности признакового пространства
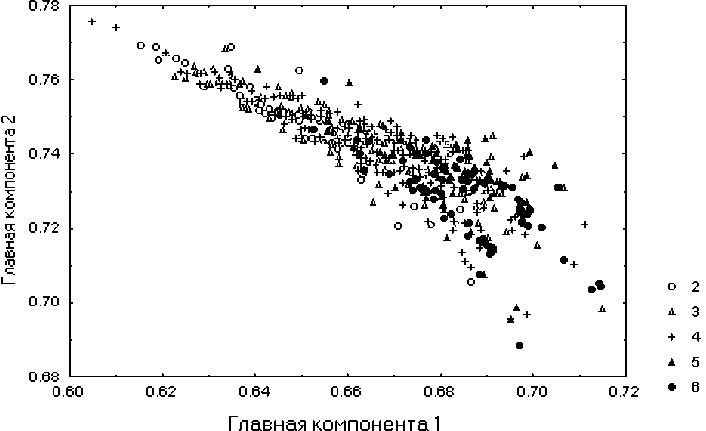
Рис.5. Изображение в пространстве двух главных компонент облака точек, соответствующих различным классам качества воды
прогнозируя значение отклика.
В нашем конкретном случае достоверность распознавания по полученной двухуровневой сетевой модели несколько снизилась по сравнению с обычным персептоном, представленным на рис.3. Однако общий смысл перехода в пространство небольшой размерности не столько в том, чтобы повысить эффективность прогноза, сколько в попытке дать какое-то содержательное объяснение имеющимся внутренним механизмам анализируемых явлений после сведения многочисленных взаимозависимых наблюдаемых переменных к немногим обобщенным ненаблюдаемым факторам. Один из способов это сделать ‒ проанализировать двух- или трехмерную визуализацию классифицируемых объектов в осях главных факторов (см. рис.5). Изучив на полученном графике сильно трангрессирующее облако точек, принадлежащих разным классам качества воды, можно, по крайней мере, оценить, какая нетривиальная задача была поставлена перед системой распознавания.
Поскольку мы ограничены рамками настоящей публикации, вне обсуждения остался материал, посвященный следующим аспектам использования нейросетевых технологий для оценки качества воды водоемов:
-
- ИНС-модели, основанные на обоих классах признаков Xи и Xв, а также сравни-
- тельный анализ их информативности;
-
- решение задачи регрессии с помощью нейросетей различной архитектуры для прогнозирования гидрохимических и гидробиологических показателей, измеренных в непрерывных шкалах;
-
- кластерный анализ и визуализация полученных наблюдений с использованием самоорганизующихся карт Кохонена;
-
- оценка класса качества вод с использованием иерархических деревьев решений.
Заинтересованный читатель может воспользоваться нашим адресом электронной почты , чтобы высказать свое мнение или получить дополнительную информацию. В приложение к списку литературы приводим некоторые использованные нами сайты, где размещены Интернет-публи-кации, ссылки и библиография по проблемам искусственного интеллекта и нейросетевых технологий: и


