Нейросети на многозначных нейроэлементав: обучение обработка и распознавание изображений

Многозначные нейроэлементы, основанные на концепции многозначных пороговых функций k-значной логики [1] были впервые предложены в [2], а затем различные аспекты их теории были развиты в [3] и [4]. Основной особенностью многозначных нейроэлементов является представление обрабатываемой информации и весов нейроэлементов с помощью комплексных чисел. На первый взгляд такое представление может показаться неестественным и слишком громоздким в чисто вычислительном аспекте, но как было показано в [1-4] оно позволяет определить выходную (активирующую) функцию нейрона таким образом, что алгоритм обучения для многозначного нейрона сходится в сотни раз быстрее, чем алгоритмы обучения для других типов нейронов, а, кроме того, функциональные возможности многозначных нейронов значительно выше, чем у других типов нейронов.

Применение нейросетей для решения задач обработки изображений вошло в широкую практику с конца 80-х годов после публикации работы Чуа-Янга [5], в которой была предложена концепция клеточной сети, весьма удобная для реализации, например различных алгоритмов линейной фильтрации. В [2] нами была предложена клеточная сеть на многозначных нейронах и ее использование в качестве ассоциативной памяти для хранения полутоновых изображений. В [3] и [4] мы рассматривали применение такой же клеточной сеги (а также клеточной сеги из универсальных бинарных нейронов [6], математическая основа которых та же, что и у многозначных, но предназначены они для реализации не многозначных пороговых, а произвольных булевых функций) для решения некоторых задач обработки изображений (фильтрация импульсного шума, выделение контуров). Главная цель настоящей работы -дальнейшее развитие теории многозначных нейронов и расширение областей их применения. Мы рассмотрим алгоритм обучения, обоснованный в [1] и [3], но с существенным усилением, позволяющим более чем в 30 раз ускорить процесс сходимости алгоритма ооучения. а также увеличить число входов нейрона и уровней оораоатывасмых сигналов с десятков и сотен до тысяч. Мы рассмотрим также новый тип сети из многозначных элементов - сеть со случайными связями, в которой каждый нейроэлемент соединен с фиксированным числом других, но не из ближайшей окрестности, как в случае клеточных сетей, а с элементами, определяемыми некоторой случайной функцией. На базе этой сети оудет предложена ассоциативная память, весьма эффективная для хранения и распознавания полутоновых изображений. Будет также рассмотрено использование клеточной сети из многозначных и универсальных бинарных нейронов дтя решения задач выделения контуров на полутоновых и бинарных изооражениях, а 1акже дтя анализа текстур.

2.МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Сначала напомним некоторые основные понятия теории многозначных и универсальных нейроэлементов. Эти нейроны реализуют полностью определенные пороговые к-значные функции, либо частично определенные k-значные функции (многозначные нейроны) и произвольные булевы функции (универсальные бинарные нейроны) от п переменных f(Xj, . . . , Хп) путем их представления при помощи п+1 комплексных параметров (весов) w„, w,,. . . , w,

f(x,,...,xn) = P(w0 + w,x, + wnx„) (1)

где X^,..., Xn-переменные, от которых зависит реализуемая функция (входы нейрона) (отмерим, что значения функции и ее переменных в многозначном (k-значном) случае кодируются комплексными числами, являющимися корнями k-ой степени из единицы ej = ехр(i 2 л j / к), j е [0, к - 1 ], i- мнимая единица; иначе говоря, значения к-зачной логики представляются корнями к-ой степени из единицы: СТ-» £ ) , а Р - выходная (активирующая ) функция нейрона, определяемая дтя многозначного нейроэлемента:

P(z) = exp(i * 2л * j / k),

(2a)

if 2л * (j + 1) / k > arg(z) > 2л * j / k где j=O,l,...,k-l - значения в k-значной логике, i - мнимая единица Z = w0 + WjXj + wnXn -взвешенная сумма , arg(z) - аргумент комплексного числа z ; и для универсального бинарного нейроэлемента:

P(z) = (-l)j if (2л (j + l)/m) > arg(z) > (2л* j/m) (2b)

где m - некоторое натуральное число, 0o + WjX, + W_nX_n , arg(z) - аргумент комплексного числа z. Переменные (входы нейрона) и реализуемая функция в данном случае булевы и принимают значения в множестве {1,-1}. Идея подобного представления многозначных функций была впервые предложена в [1], а булевых - в [6]. Определение выходных

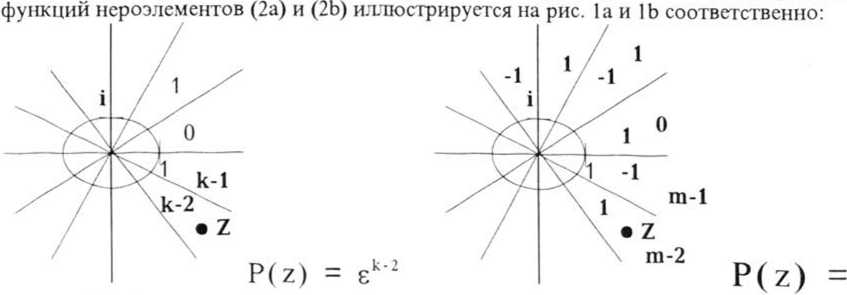
Рис. 1а                                       Рис. 1Ь

З.УСОВЕРШЕНСТВОВАННЫЙ АЛГОРИТМ ОБУЧЕНИЯ

Из описанной математической модели очевидно, что обучение для обоих рассматриваемых типов нейронов состоит в "напрравлении" взвешенной суммы входных сигналов в нужный сектор на комплексной плоскости (из к возможных дтя многозначного и из m возможных дтя унивсрсальног бинарного нейрона) (Рис.1). Алгоритм обучения дтя многозначного нейроэлемента был предложен в [1], и затем ряд его модификаций был предложен в [2-4]. Многочисленные эксперименты показали, что скорость сходимости этого алгоритма существенно выше скорости сходимости алгоритмов обучения дтя нейронов Хопфилда, Чуа и других подобных классических" нейроэлементов.

Процедура "направления" взвешенной суммы в нужный сектор комплексной плоскости (иначе говоря, процедура коррекции вектора структуры) определяется следующим правилом [1р

wm„ = Wm + ЮЕ-X ,                (3)

где and ^^т+1 ' текущий и следующий весовые векторы (векторы структуры), W -коэффициент коррекции!, X - вектор входных сигналов нейрона с комплексно-сопряженными с 4

компонентами, с, - значение функции на выходе (выходной сигнал нейрона), таким образом, q -номер нужного сектора (иначе говоря, q - целочисленное значение k-значной функции, реализуемой нейроном). W выбирается так, чтобы значение взвешенной суммы Z = W_o + WjXj + W_nX_n было как можно ближе к нужному сектору (либо сразу же попадало в него) ( к сектору с номером q ) после шага обучения, определяемого правилом (3). Как правило, достаточно рассмотреть всего два случая для выбора w-|arg(E⁴) - arg(z)| < тс / 2 или |arg(£⁴) - arg(z)| >  к / 2. Если выполняется первое из этих условий, как правило достаточно одной-двух итераций для попадания в нужный сектор по правилу (3). Для второго случая число итераций, как правило, несколько больше, но более чем на порядок. Под "итерацией" следует понимать последовательную проверку (1) для всех элементов обучающего множества, и в том случае, если (1) не выполняется для некоторого элемента из этого множества, для коррекции весов применяется обучающая процедура (3). Этот процесс продолжается до тех пор, пока не будет получен вектор структуры W=( W_o, W,, . . . W_n ), удовлетворяющий (1) для всех элементов обучающего множества. Как показывают экспериментальные данные, процесс обучения, определяемый правилом (3), сходится для большинства частично определенных функций k-значной логики. В [1] доказано, что процесс обучения сходится также для полностью определенных многозначных пороговых функций. Даже в случае несходящегося процесса для некоторой функции (в частности, для частично определенной функции) практически всегда можно так изменить значение к, чтобы свести нереализуемую на нейроне функцию k-значной логики к реализуемой функции k-значной логики (k < к или к > к), дтя которой процесс обучения сходится.

Непосредственное применение арифметики с плавающей запятой к вычислениям с комплексными числами в (3) позволяет реализовать алгоритм обучения, однако с ростом кип (числа переменных) вычисления все более замедляются и, например для обучения сети из 4096 нейронов (каждый из них имеет 30 входов, к=256, обучающее множество дтя каждого нейрона состоит из 30 элементов) требуется 70 часов на компьютере класса 486-DX2-66 Mhz. Модификация алгоритма обучения, которая сейчас будет рассмотрена, позволяет с одной стороны ускорить процесс обучения примерно в 30 раз, а с другой стороны обучать нейроны с числом входов, равным п= 1000-2000 реализации функций к= 2000-4000 - значной логики.

Прежде всего откажемся от вычислений с плавающей запятой. Действительную и мнимую часть весов будем представлять в виде 32-битовых целых чисел, а взвешенную сумму - 64-битовым целым числом. Для ускорения вычисления выходного значения нейроэлемента, т.е., дтя ускорения вычислений в (2а) необходимо наложить несущественное ограничение на возможные значения к, а именно, к должно быть кратно 8. Несущественность этого ограничения очевидна, т.к. при необходимости значение к всегда можно увеличить до необходимого. Зато благодаря этому ограничению мы можем вычислить j (целочисленное значение функции на выходе нейрона, соответствующее комплексному £ ), прибегая к существенно меньшим вычислительным затратам. Пусть z = (Re(z), Im(z)) - комплексрое число, представляющее взвешенную сумму и a/?5(Re(z) / s(Re(z)) > o/?s(Im(z)

Вместо вычисления arg(z) путем многочисленных сравнений аргументов взвешенной суммы и корней соответствующей степени из единицы мы будем вычислять значение j функции на выходе нейрона непосредственно, пользуясь заранее созданной таблицей:

(/) = /g(2n/ / А), где/ = 0, 1,... , (А / 8) - 1                 (5)

Из (4), (5) и Рис. 2 очевидно, что очень легко может быть найдено такое значение /, что ( 2) < ф < Т( 1 1  . Принимая во внимание знак и значение отношения Im(z)/Re(z) , лет ко найти номер s "подсектора", в который попадает z. Теперь очевидно, что

7 = s(A/8) + /, s = 0,l,...,(А/8)-1,(6)

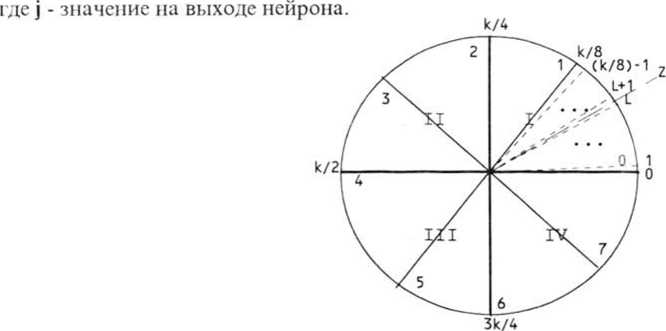
Рис. 2

Теперь вернемся к примеру с сетью, содержащей 4096 30-входовых нейронов, для которой решается задача обучения на обучающем множестве, содержащем 30 элементов (мы еще раз вернемся ниже к применению этой сети). Использование того же правила обучения (3), ио с учетом (4)-(6) позволяют решить задачу обучения за 2 часа 25 минут на том же компьютере класса 486 DX2-66 Mhz (без использования модификации (4)-(6) та же задача решается за 70 часов).

Следует сделать ряд замечаний по поводу обучения универсального бинарного нейрона.Очевидны два плдхода к решению этой задачи. Первый основывается на непосредственном использовании процедуры (3). 8 4 в этом случае соответствует правой границе того сектора на комплексной плоскости, в который должна попасть взвешенная сумма Z = Wy+WjXj +wnxn (Рис. la). Если Z попадает "не в тот" сектор, веса должны быть скорректированы в соответствии с (3), чтобы направить Z в соседний сектор. Исходя из этих соображений, значения коэффициента коррекции СО в (3) определяются следующим образом ( i-мнимая единица):

, 1, if Z должно "переместиться" в правый сектор/ 7 \

. i, if Z должно "переместиться" в левый сектор* ' /

Экспериментально показано, что подобный процесс обучения довольно быстро сходится прежде всего для достаточно малых m (см. (2Ь) ) (например, при т=4 для функций, допускающих представление (1) достаточно как правило не более 100 итераций для сходимости алгоритма обучения). Другой подход к обучению универсального бинарного нейрона сводится к преобразованию булевой функции в m-значную (каждая "1" преобразуется в некоторое четное значение, каждая "-1” - в некоторое нечетное) и затем к применению алгоритма обучения (3)-(6) к полученной многозначной функции. Однако, подробное обсуждение этой проблемы выходит за рамки данной работы. Один из подходов к ее решению предложен в [4].

• 4.    СЕТИ ИЗ МНОГОЗНАЧНЫХ И УНИВЕРСАЛЬНЫХ ЭЛЕМЕНТОВ И ИХ ПРИМЕНЕНИЕ ДЛЯ ОБРАБОТКИ И РАСПОЗНАВАНИЯ ИЗОБРАЖЕНИЙ

Обе разновидности рассматриваемого нейроэлемента очень удобны для создания сегей, предназначенных в первую очередь для обработки и распознавания изображений. Мы предлагаем использован, два типа сетей. Первая из них клеточная, в которой каждый нейрон соединен только с нейронами из своей ближайшей прямоугольной (квадратной) окресгносги Хотим, однако, обратить внимание, что это не клеточная сеть Чуа [5], т.к. базисные нейроны нашей сети и сети Чуа совершенно различны. Второй тип сети, который мы хотим предложить, это сеть со случайными связями (каждый нейрон в такой сети соединен, как и в клеточной сети, с щраниченным числом других нейронов, но их координаты определяются некоторой случайной

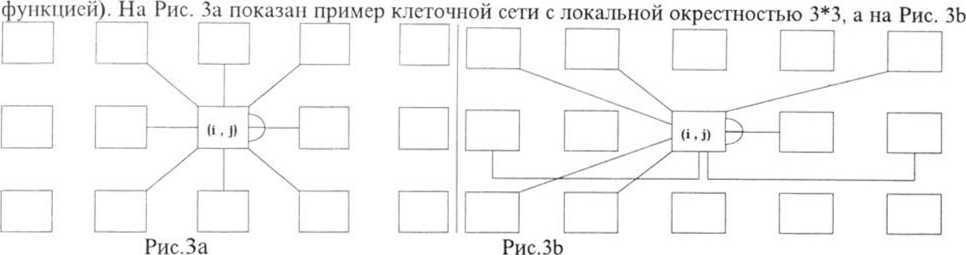
показан пример сети со случайными связями, в которой каждый (ij-тый) нейрон соединен с восемью другими и имеет обратную связь.

ВЫДЕЛЕНИЕ КОНТУРОВ

Первым, весьма эффектным и эффективным применением клеточной сети является решение на ней задачи выделения контуров на полутоновых изображениях. В качестве базового элемента сети будем использовать универсальный бинарный нейроэлемент. Алгоритм выделения контуров состоит из следующих шагов: 1.Полутоновое изображение с 256-ю градациями яркости разбивается на 8 битовых плоскостей; 2.На каждой битовой плоскости, представляющей собой бинарное изображение, производится выделение контуров; 3.Осуществляется “сшивание” бинарных контурных изображений в полутоновое.

Выделение контуров на бинарном изображении исчерпывающим образом описывается следующей булевой функцией :

X X, Х₃ 1

= х9 = 1

,...х4х6,...х9*1

-1, если х5=-1 или X] =...=х5=...

Y Х4 Х5 Х6 =   | еслих5=1 и хотя бы один из X]

Х7

XR

х9

другими словами, контур регистрируется в данной точке, если он проходит через центральную точку окна 3*3 , окружающего данную точку. Пусть т=4 в (2Ь). Применение алгоритма обучения (7) к функции (8) дает сходимость после 51 итерации (на которые затрачивается всего несколько секунд на компьютере класса 486 DX2-66 Mhz. Получив в результате обучения необходимый набор весов, мы можем решать задачу выделения контуров на нейросети. Отметим, что при аппаратной реализации сети можно сделать ее восьмиуровневой, чтобы обрабатывать каждую битовую плоскость параллельно в режиме реального времени. На рисунках 4а и 5а показаны оригинальные изображения, на которых проводилось выделение контуров описываемым методом. На рисунках 4Ь и 5Ь показан результат обработки, а на рисунках 4с и 5с - результат выделния контуров на тех же изображениях при помощи оператора Лапласа. Преимущества описанного здесь подхода очевидны хотя бы из того, что он позволяет выделить как малейшие пе-

Рис.5а

рспады яркостей, так и даже контуры “смазанных”, нерезких деталей.

СЕГМЕНТА ЦИЯ И А НАЛИЗ ТЕКСТУР

На такой же клеточной сети, но построенной из многозначных нейронов, можно эффективно решать задачу анализа текстур. Для этого, очевидно, следует в процессе обучения добиться того, чтобы многозначный нейроэлемент различал необходимые текстуры. Естественно, результат будет тем лучше, чем большие по площади участки эталонных текстур будут присутствовать в обучающей выборке. При этом естественно следует учесть, что время, затрачиваемое на обучение, будет увеличиваться. Так что, следует искать “золотую середину” между мощностью обучающего множества и временем обучения. Проблема существенно упрощается при использовании высокопроизводительной вычислительной техники типа рабочих станций. На рис. 6 представлены два текстурных изображения размера 64*64, составивших обучающее множество. Первое из этих изображений представляет собой поле из случайных чисел с равномерным, а второе - с гауссовским распределением. Обучение многозначного нейроэлемента с 91-м входом (нейрон соединен со всеми нейронами из своей локальной окрестности 9*9) по алгоритму (3)-(6) на компьютере класса 486-DX2-66Mhz потребовало около 60 часов. Для проверки обученной сети было предложено проанализировать изображение на рис.7, где на равномерное поле

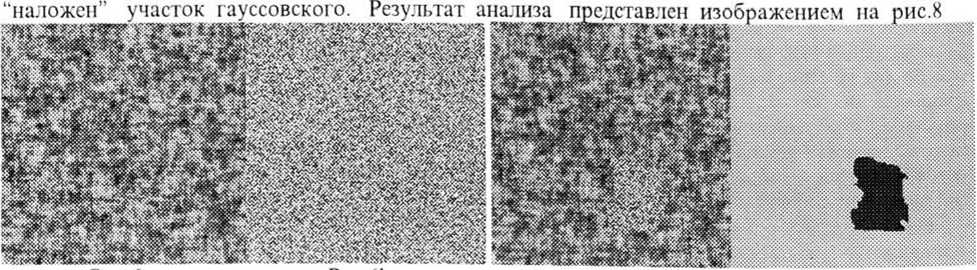
. Как видим, разделение текстур произошло абсолютно правильно. Очевидным достоинством данного метода являстся 1акже высокая толерантность обученного нейроэлемента (или сеги - в данном случае, как и в случае выделения контуров все нейроны сети реализуют одну и ту же функцию) к поворотам эталонных образов.

РАСПОЗНАВАННЕ И ХРАНЕНИЕ ИЗОБРАЖЕНИЙ В АССОЦИА ТИВНОЙ ПАМЯТИ

Ассоциативная память, т.е., память, адресуемая по содержанию, являстся эффективным средством не только для хранения данных, но и дтя их распознавания, точнее - узнавания в условиях зашумленности, частичного искажения и т.д. Создание подобных систем памяти, базирующихся на нейроподобных сетях, для полутоновых изображений впервые было предложено Т.Кохонсном [7]. В [2] нами была предложена модель ассоциативной памяти дтя полутоновых изображений, базирующейся на клеточной сеги из многозначных нейронов. Недостатком такого подхода является невозможность узнавания изображения в случае полного разрушения какого-то сто фрагмента , поскольку ограниченность связей в клеточной сети не позволяет восстановить полностью утраченный фра! мент. Этот недостаток преодолевается, если в качестве базовой сеги дтя ассоциативной памяти избра л, сел. со случайными связями , описанную выше.

Для проверки работы подобной ассоциативной памяти была разработана программная модель сети, содержащей 4096 многозначных (в данном случае - 256-значных) нейроэлементов с 30

входами каждый. Множество нейронов, соединенных с каждым данным определялось с помощью датчика случайных чисел (вертикалыпас и горизонтальные координаты отдельно). Обучающее множество содержало 40 полутоновых изображений с 256-ю градациями яркости различных

Рис.9

думать, что на размеры наложено какое-то ограничение, поскольку в данном случае выбор размера определялся исключительно желанием ускорить обучение в условиях моделирования сети на обычном компьютере класса 486 DX2-66. Обучение всех нейронов сеги, построенное по алгоритму (3)-(6), занимает 3 часа 20 минут при наличии у каждого нейрона обратной связи (один вход соединен с собственным выходом) и 5 часов 15 минут без обратной связи. Отметим, что наличие или отсутствие обратной связи, как показывают эксперименты, не оказывает в данном случае решающего влияния на свойства ассоциативной памяти. Отличные же возможности

памяти демонстрируют эксперименты, иллюстрируемые на рис. 10 и 11. На рис. 10а представлено одно из изображений обучающей выборки , в котором 75% информации заменено равномерным шумом. На рис. 10b - результат восстановления (узнавания) изображения после 20-ти итераций работы сети (под итерацией понимается сраба тывание всех нейронов сет), на рис. Юс - результат

Рис.10а                        Рис.ЮЬ                        Рис.Юс

восстановления изображения после 40 итераций работы сеги. Очевидно, что уже качества изображения после 20-ти итераций достаточно для его распознавания, но после 40 итераций полученное изображение вообще практически нс отличается от оригинала (срсднсквадратическос отклонение - 0.87). На рис.11а показано то же изображение из обучающей выборки,

“испорченное” импульсным шумом с вероятностью искажения отсчетов 0.3. На рис. 11b -ажения после 35- ги, а на ис. 11с- после 70-т и итераций аботы

сзультат восстановления изоб

Рис.11Ь

Рис.11а сеги. Вновь промежуточного

Рис.11с

результата вполне достаточно для узнавания изображения, а

окончательный результат восстановления вновь практически не отличается от оригинала. Значительно более высокая эффективность данного подхода по сравнению с изложенным в [8], где

на изображениях того же размера допускалось искажение не более 25 “о информации (иначе оно нс восстанавливалось) нс вызывает сомнений.

• 5.    ЗАКЛЮЧЕНИЕ

Основной вывод, который можно сделать по результатам данной работы - это весьма высокая эффективность многозначных нейроэлементов (и их разновидности - универсальных бинарных нейроэлементов) по сравнению с другими типами нейроэлементов прежде всего благодаря алгоритму обучения, свободному как от решения сложных систем линейных неравенств, так и систем дифференциальных уравнений (либо то, либо другое необходимо для любых других типов нейроэлементов). Наличие эффективного алгоритма обучения позволяет решать с помощью различных типов сетей, построенных из рассматриваемых нейроэлементов, широкий круг задач, и в частности, как было показано, весьма эффективно решать задачи обработки и распознавания изображений: выделения контуров, анализ текстур, хранение и распознавание изображений в ассоциативной памяти, получая при этом результаты, как превосходящие тс, что получаются при применении других методов решения тех же задач, так и те, что получаются при применении других типов нейросетей и иных базовых нейроэлементов.