Нейроуправление активными источниками для подавления акустических волн в заданной области

Шум является одним из неблагоприятных факторов окружающей среды. Для уменьшения шума применяются как пассивные средства (звукопоглощающие материалы), так и активные методы подавления шума, основанные на взаимодействии пассивных акустических волн и волн от активных источников, которые, например, генерируют соответствующие волны в противофазе.

Современные схемы активного гашения звука представляют собой достаточно сложные адаптивные системы [1–3], которые позволяют снижать интенсивность акустических полей в заданной области, уменьшать излучаемую звуковую энергию в целом и осуществлять адаптивное управление в зависимости от поставленных задач. Следует отметить перспективность нейросетевых методов управления активными акустическими источниками, которые после настройки и обучения управляющих нейросетевых блоков обладают высокой скоростью обработки информации и позволяют управлять снижением шума в режиме реального времени.

Численное моделирование распространения и взаимодействия акустических волн проводится на основе численной схемы С. К. Годунова [4] в двумерной постановке. Рассматривается прямоугольная область D (10 × 2,5 м), на границах области предполагается полное отражение акустических волн. Для расчета используется двумерная сетка элементов A j с параметрами h x = h y = 0,1 м; i = 1,2, …, 100; j = 1,2, … 25 (рис. 1).

акустического давления S определена в виде объединения ячеек S = U А i **** j , где i   = 90, j = 1,2, .., 25.

В ячейках воздействия источников E, F1 и F2 генерируется акустическое давление в виде pE (A, v, t) = A sin(2nvt), pF (Bi, wi, t) = Bi sin(2nwi t).             (1)

Здесь A и B i ( i = 1,2) – амплитуды звукового давления (для того чтобы в (1) не использовать фазовый сдвиг при изменении параметров амплитуд, предполагалось, что эти параметры могут принимать как положительные, так и отрицательные значения), v и w i ( i = 1,2) – частоты звукового давления.

Для контроля квадратичной величины звукового давления в области S рассматривается интегральная характеристика вида

Q ( B 1 , B 2 , W 1 , W 2 , t ) = JJ ( p ( x , y , t ) ) ² dxdy . (2)

S

Общая интегральная оценка уровня квадратичной величины давления в зоне контроля S для заданного интервала времени [0, t ^*] определяется в следующей форме:

t y = J Q (B1, B 2, W1, W2, t) dt.             (3)

Здесь t ^* соответствует времени двукратного пробега звуковой волны вдоль расчетной области.

Из соотношений (2) и (3) следует, что среднее звуковое давление в контрольной области S площадью ц(S) с учетом его изменения во времени можно оце- нить по выражению

D

E F 1

S

F 2

Рис. 1. Вид расчетной области D с выделенной подобластью S для контроля акустического давления и расположение пассивного источника E и двух активных источников F ₁ и F ₂

Пассивное акустическое воздействие рассматривается в ячейке Аi*j*, где i =5, j = 5. Источники F 1 и F2, управляемые нейронной сетью, активные, располагаются в ячейках Аi**j**, i = 5, j = 6 и Аi***,***, i = 1, j*** = 12 соответственно. Выбор места расположения этих акустических источников для снижения уровня давления в области S исследован в [5]. Зона контроля pcp

Y

^*

T ц ( S )

.

Нейросетевое управление параметрами давления активных источников F 1 и F 2 осуществляется на основе инверсной модели объекта управления [6] (рис. 2). Представлены прямая (рис. 2, а ) и инверсная (рис. 2, б ) модели объекта управления.

Архитектура нейронной сети выбрана в виде обобщенной регрессионной сети [7], обладающей высокой скоростью обучения. Объект управления представляет собой двумерную акустическую модель, которой соответствует протестированный вычислительный модуль [8], разработанный на основе схемы С. К. Годунова для моделирования нестационарного распределения акустического давления p ( x , y , t ) в расчетной области D в зависимости от варьируемых параметров A , v , B i , w i .

pE

p

p

Объект управления

QQ pE

Нейронная сеть

p

F 1

pF2

а                                        б

Рис. 2. Модели объекта управления: а – прямая; б – инверсная

После включения блока управления на вход нейронной сети подаются изменяющаяся величина давления в пассивном источнике и нулевые значения для контролируемого параметра Q , так как это соответствует для данной модели инверсного управления максимальному снижению давления в контролируемой зоне S .

Исследование аналогичной схемы управления для одного активного источника было рассмотрено в [9]. Выходом нейронной сети является значение давлений двух акустических источников в текущий момент времени t :

T = ( pF, pF2)

Входной вектор имеет вид:

P(R) = [pt-4At, pt-3At, pt-2At, pt-At, ET pt , Qt-4At, Qt-3At, Qt-2At, Qt-At, Qt J , где ptE4T,..., pE являются значениями пассивного источника в пять моментов времени с запаздыванием относительно текущего времени; Qt-4т, ..., Qt представляют пять соответствующих значений квадратичной величины давления в зоне контроля S; At - время запаздывания – соответствует каждому численному шагу по времени (At = 131); R - размер входных данных для нейронной сети (R = 10).

Обучение нейронной сети производится на предварительно сформированных данных: входных векторах P и соответствующих им выходных значениях T . Формирование набора данных осуществляется перебором параметров A , B i , v , w i , которые по формуле (1) определяют значения давлений пассивного и активных источников, где амплитуды A и B ₁ изменяются в диапазоне [–15 Па, 15 Па] с интервалом 10 Па, амплитуда B 2 – в диапазоне [–5 Па, 5 Па] с интервалом 2,5 Па, а частоты v , w 1 и w 2 – в диапазоне [70 Гц, 130 Гц] с интервалом 30 Гц. При этом проводится численное решение по двумерной акустической модели и вычисляются значения контролируемой величины Q ( B 1 , B 2 , w 1 , w 2 , t ) по формуле (2).

Настройка нейронной сети осуществляется подбором параметра spread [10]. Чем больше значение этого параметра, тем большее число нейронов участвует в формировании среднего значения, и наоборот. Установлено в вычислительных экспериментах, что для данной модели наиболее эффективным является значение этого параметра, равное 0,1.

Проведенные вычислительные эксперименты позволяют сравнить результаты нейросетевого управления параметрами двух активных источников с результатами прямой минимизации акустического давления в контролируемой области S на основе гибридного генетического алгоритма [5].

Изменение давления пассивного источника E в виде p^E ( A, v , t ) = 10sin(2 n 100 1 ) не входит в обучающую выборку для нейронной сети, поэтому эффективные значения изменений активных источников определяются нейронной сетью аппроксимационно (при предполагаемых нулевых значениях параметра Q (2)). В результате расчетов получены значения численной оценки V = 1,279 1 и среднего давления в контролируемой подобласти p ^ср = 0,010 7 Па.

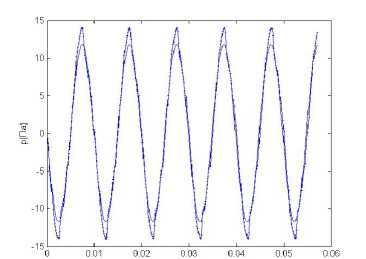
С помощью вычислительного эксперимента по минимизации акустического давления в части заданной области с помощью гибридного генетического алгоритма при описанной выше функции распространения давления пассивного источника установлено, что оптимальными параметрами активных источников для минимизации звукового давления в определенной зоне области являются значения: B 1 = –11,76 Па, w 1 = 100,43 Гц, B 2 = 1,69 Па, w 2 = 101,01 Гц. При этих параметрах значение численной оценки V = 0,23, а среднее давление в зоне контроля p ^ср = 0,004 6 Па. Графики изменения давления в активных источниках F 1 ( а ) и F 2 ( б ) при минимизации и вариант при нейроуправлении этими источниками представлены на рис. 3.

Для сравнения с результатами при отсутствии активных источников F 1 и F 2 : оценка уровня давления в контролируемой подобласти составляет V = 760,48, а p ^ср = 0,261 7 Па.

Для наглядного представления различий распределения давления в двумерной расчетной области D на рис. 4–7 в характерные моменты времени ( t ^*/4, t ^*/2, 3 t ^*/4, t ^*) приведены поверхности распределения давлений для трех вариантов расчетов: а ) – показана поверхность изменения давления при отсутствии активных источников; б ) представлена поверхность давления при действии активных источников с оптимальными параметрами, полученными из решения задачи минимизации звукового давления в зоне контроля на основе гибридного генетического алгоритма; в ) представлена поверхность давления при действии активных источников, которые управляются нейросетевым блоком в режиме реального времени.

ты

б

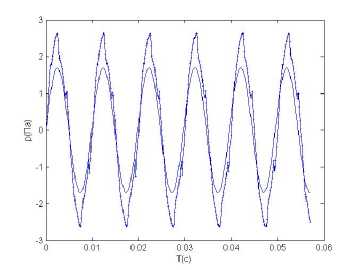
Рис. 3. Графики сравнения изменения давления в двух активных источниках при прямой минимизации на основе гибридного генетического алгоритма и при нейроуправлении:

а – источник F 1 ; б – источник F 2

а

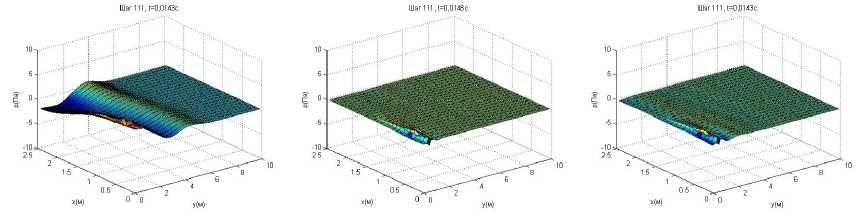
а                                б

в

Рис. 4. Поверхности звукового давления в момент времени t ^*/4 для трех вариантов расчетов

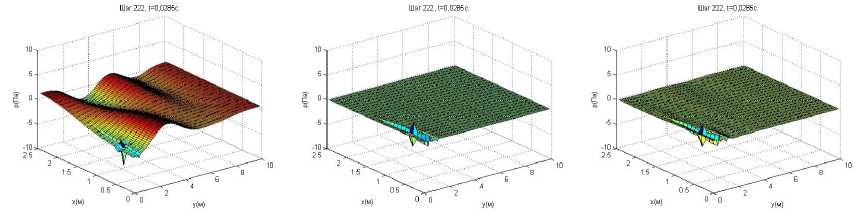
а                                  б                                  в

Рис. 5. Поверхности звукового давления в момент времени t ^*/2 для трех вариантов расчетов

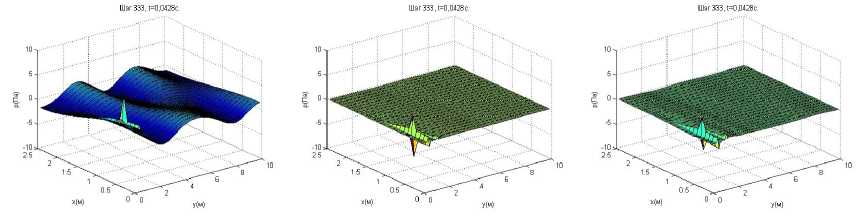
а                                б

в

Рис. 6. Поверхности звукового давления в момент времени 3 t ^*/4 для трех вариантов расчетов

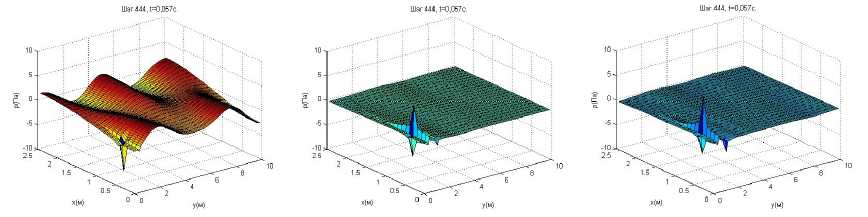
а                                  б                                  в

Рис. 7. Поверхности звукового давления в момент времени t ^* для трех вариантов расчетов

Результаты расчетов показывают, что уровень акустического давления в зоне контроля S , достигнутый при прямой минимизации давления с помощью гибридного генетического алгоритма, ниже, чем уровень звукового давления в зоне контроля S для варианта нейроуправления активными источниками. Если оценивать по среднему давлению p ^ср, снижение звукового давления в зоне контроля S в первом случае в 57 раз, а во втором – в 24 раза.

Следует отметить, что значительно большее снижение давления в контрольной области при прямой минимизации акустического давления по параметрам активных источников достигнуто для конкретного вида изменения давления пассивного источника. Использование же нейросетевого управления хотя и не обеспечивает столь значительных результатов, но при этом дает возможность понизить акустическое давление в контрольной области и для других форм изменения давления в пассивном источнике, а также проводить процесс управления в режиме реального времени.

Итак, результаты вычислительных экспериментов по применению нейросетевого блока управления двух акустических источников, основанного на инверсной модели объекта управления с учетом граничных условий (полное отражение волн от границ области) свидетельствуют о возможности значительного подавления акустического давления в зоне контроля. Примененная схема управления позволяет рассматривать адаптивный процесс управления при изменяющейся форме давления пассивного источника, а также при электронной реализации нейросетевого блока управления проводить управление в режиме реального времени.