Нейтрино в остывающей Вселенной

Современная теория элементарных частиц – стандартная модель – включает в себя электрослабую модель, описывающую электромагнитные и слабые взаимодействия частиц, и квантовую хромодинамику, описывающую сильные взаимодействия кварков [1]. Стандартная модель представляет собой калибровочную теорию с группой SU(3) х SU(2) х U(1), в которой подгруппа SU(3) отвечает квантовой хромодинамике, а множитель SU(2) х U(1) соответствует электрослабой модели. Стандартная модель убедительно подтверждена открытием бозона Хиггса в экспериментах на Большом адронном коллайдере (БАК). Несмотря на это, она не лишена недостатков, например, таких как присутствие в теории около двух десятков свободных параметров никак не объясняемых в рамках модели. Также среди них нет параметра, описывающего предельный вариант теории при высоких тем- пературах, характерных для начальных мгновений существования Вселенной после ее возникновения в результате Большого взрыва [2].

В работах [3–5] выдвинута гипотеза о том, что калибровочная группа стандартной модели становится проще с увеличением температуры Вселенной, а механизмом изменения калибровочной группы предложена операция контракции [6, 7], параметр которой уменьшается при увеличении температуры е ~ T-q ^ 0 при T ^ ж (q > 0). В результате контракции лагранжиан стандартной модели представляется в виде слагаемых, которые различаются степенями параметра ϵ. Таким образом, двигаясь вперед во времени, т. е. в обратном к высокотемпературной контракции направлении, заключаем, что после рождения Вселенной частицы и их взаимодействия проходят ряд стадий в эволюции от предельного состояния с ”бесконечной” температурой до состояния, описываемого канонической стандартной моделью. Эти стадии формирования кварк-глюонной плазмы, восстановления элек-трослабой и цветовой симметрий различаются по степеням контракционного параметра и, следовательно, по времени их возникновения.

Анализ доминантного механизма рождения и регистрации бозонов Хиггса на БАК и сравнение с экспериментальными данными, полученными на БАК по сечениям рождения бозонов Хиггса при энергиях 7,8,13 и 14 ТэВ [8], показывает, что гипотеза о контракции калибровочной группы стандартной модели при высоких температурах как минимум не противоречит эксперименту [9–11].

Наличие непрерывно изменяющегося параметра ϵ ∼ T ^-q свидетельствует о перераспределении роли отдельных слагаемых в лагранжиане электрослабой модели при б ^ 0 , т. е. об изменении относительного вклада частиц и их взаимодействий в формирование космической плазмы по мере остывания Вселенной. Естественно предположить, что этот процесс не останавливается на рубеже спонтанного нарушения симметрии, но продолжается и при дальнейшем остывании. В данной работе мы рассмотрим деформацию калибровочной группы электрослабой модели при температурах меньших 100 ГэВ, и ее влияние на процессы с участием нейтрино.

1. Электрослабая модель при низких температурах

Электрослабая модель, описывающая электромагнитные и слабые взаимодействия элементарных частиц, представляет собой [12] калибровочную теорию с калибровочной группой SU (2) х U (1) , действующей в двумерном комплексном пространстве полей C 2 :

SU(2) : z ‘ = Gz,

(z2) = (-в а)(z2) • № + iei2 = 1•

U (1) : z' = еш/2 z = e1^ Z, ш € R. (1)

В качестве C ₂ берутся лептонное пространство, состоящее из векторов ^ν _e ^e , где e есть электрон, а ν _e обозначает электронное нейтрино и кварковое пространство, содержащее поля u - и d -кварков ^u_d . (Мы ограничимся только первыми поколениями лептонов и кварков). Лагранжиан модели, равный сумме бозонного, лептонного и кваркового лагранжианов выбирается инвариантным относительно действия калибровочной группы.

В данной конструкции частицы задаются компонентами векторов из пространств представления, а взаимодействия между ними описываются элементами калибровочной группы. Согласованное переопределение элементов группы SU (2) и компонент векторов пространства С ₂

( z 1 ) ( ) ’ )( z 1 )

ez2 J --Ф й J ez2 ) (2)

при б = 0 приводит к деформированной полупростой группе SU (2; б ) , изоморфной SU (2) , а в пределе б ^ 0 дает неполупростую группу SU (2; б = 0) , изоморфную евклидовой группе E (2) , действующей в расслоенном пространстве C ₂ ( б = 0) с базой, натянутой на первую координату {z 1 } , и слоем, порождаемым второй координатой {z ₂ } . В эквивалентной форме преобразование (2) записывается как действие деформированной матрицы на неде-формированный вектор в виде

( z 2 ) = ( —в б а )( z 2 )■ (3)

Деформация (2), (3) канонической электрослабой модели описывает ее поведение при высоких температурах, превышающих 100 ГэВ [3–5, 9, 10], характерных для ранних стадий развития Вселенной вскоре после ее рождения в результате Большого взрыва [2]. При этом вторые компоненты векторов, образованных лептонными и кварковыми полями, уменьшаются с уменьшением б ( T ) = AT ^-q , q >  0 , A = const , где T температура Вселенной, и в пределе б ^ 0 ( T ^ ж ) превосходят первую компоненту. Наоборот, при понижении температуры Вселенной вследствие ее расширения, вторые компоненты векторов увеличиваются по сравнению с первыми. Таким образом, на рубеже б ~ 1 ( T ~ 100 ГэВ ) происходит структурная перестройка описания электрослабой модели от предела высоких температур к пределу низких температур, которой отвечает согласованное преобразование калибровочной группы SU (2; £ ) и пространства C ₂ ( £ )

( С 1 ) _ ( а £в ) ( £z, ) ,„ < z2 J = V -Св а ) z z2 ) (4)

с зависимостью безразмерного параметра ξ от температуры вида £ ( T ) = BT p , p >  0 , B = const . Эквивалентно преобразование (4) можно записать как действие деформированной матрицы на недеформированный вектор

(z2)=(—аs а)(z2)■ (5)

Выбор между (2) и (3) или (4) и (5) диктуется соображениями удобства. В частности, формулы (2), (4) и вытекающие из них правила преобразования полей удобны для получения лагранжиана деформированной электрослабой модели из стандартного лагранжиана.

Подчеркнем, что преобразованные матрицы калибровочной группы в формулах (2) и (4), в отличие от (3) и (5), одинаковы. Различаются только преобразования компонент векторов (полей) из пространств представления, поэтому преобразования калибровочных полей и поля бозона Хиггса останутся такими же, как и в случае высоких энергий [10], а левые и правые компоненты лептонных и кварковых полей преобразуются как компоненты вектора z в (4). Таким образом, низкотемпературный предел электросла-бой модели достигается подстановками

Wµ± → ξWµ± , Zµ → Zµ , Aµ → Aµ , χ → χ, v → v, el → el , er → er , dl → dl , dr → dr ,

ν l → ξν l , u l → ξu l u r → ξu r .        (6)

В результате преобразований (6) бозонный лагранжиан [10, 11] можно представить в виде

L в ⁽ € ) =

Канонический лептонный лагранжиан [10, 11] через поля электронов и нейтрино преобразуется к виду f            f      I f int I £2 ( т I Tint)

L L ^{( €} ) = L L, 0 + L L, о + ^€ L LL, 2 + L L,2 J ,    ⁽¹³⁾

где

L l, о = e^if ^ d ^ e i + е Г if e d e e r - m e ( e r e i + e ] e _r ) , (14)

— f t int , г2 ( т .tint ) । _c I fint

= L B, 0 + L B, 0 + ^€ L BB, 2 + L B,2 J + ^€ L B, 4 ,    (7)

L l, 2 = v l ir^v i ,

где

L B, о = - 4 F ev ^- 4 ^Z f2v + 2 m Z ⁽ Z e ^{) 2} +

+j(^x)2—2 mXx2,(8)

= - 11V W- + mLW+W-,(9)

B,2     2 ^Vv^y VW ¹ m W e Д ’

L Bt = ^{- x}% ^{4 -} ^v^{x 3} + ₂ g_s ^ ^x ( Z e ^{) 2 +} 4             2 COS ^ W

+ я gL x2 (Zv)2 ,(10)

• 8 cos² 9 _W

int         +   - g2 2   +

• B, 2    g ^x v p, v i 4 ^x у v v w у

• -2ig (Wp+ W- - W-W-) (FpV sin 0w+Z^ cos 0w)

• - 2 [ A p ( W + W - - W - W - ) -

• LL,0   g cos 0werTeAeer  g sin Ow^TTpZper

  -hex(eTei + e^er) - g a -[tZe**’    (16)

2 COS 0w fint r ,       g cos 2 0w r „

L = ev ^ Tp ApVi + —v^Tp Z_uv_t +

L, ^{2        l p p l} ' 2cos 0 _w ^{l e e l} '

⁺ ^/2 ( ^{v l T} e ^W + ^e i ^{+ e l T} e ^W - ^v i ) '      ⁽¹⁷⁾

Кварковый лагранжиан [10, 11] представляется в виде слагаемых f            f       I f int I л 2 ( т I  Tint ) (lax

L Q ^{( €} ) = L Q, 0 + L Q, 0 + ^€ L ^Q, 2 + ^l q, 2) ,   ⁽¹⁸⁾

где

L Q, 0 =

= d^Tp d pdi + d T iT e d e d r - m d ( d r d i + d ^ d r ) , (19)

L Q, 2 =

= и ] ifd e ЦП + U r ifp d pUr - m u ( u r u i + ufa ) , (20)

-A ν W µ ⁺ ν W µ^- -W µ^-ν W µ ⁺ -

• -    ig cos O w [ Z e ( W - W - - W - W - ) -

  -Z v ( W W -   W - Wp ^-)] -

• -    -4 {[(W■) + ( W--) ] ( A )2 - - 2 (Wp-W+ + W--W-) AeAv +

+ [( W + )² + ( W - )²] ( A e )²} -

int

Q, 0 ⁼

2 | cos O w + g -sin 0^

d^ e Z e d i ^-

^- dA^ ie A ^A e d i ^- h d x ⁽ d r d i + d i d r )+

+ 3 g ‘ (sin 0 w d rT Zdd_r

^{cos 0} w d re AAdrr ) ,

т int __

^L Q, 2 ⁼

y UT A A p U i - h u x ( ufa + u \ u r ) +

+ ^cos 0 w

-

6 sin 0 w^ Цт e Z a u i +

-^g cos 0 W {[( Wp ^-) 2 + ( W - ^- )²] ( Z v )² -                + ^ ( ^{u | t} p ^WP + d i + d . ^W - u i ) +

• - 2 W -- W - + W -^- W -) Z . Z +

[( W — )² + ( W - )²] ( Z e )²} -

-eg cos 0 w W e-- W -^- A ^ Z _v + W - W ^- A e Z e -

• -2 (Wp- W- + W+ W-) (AAZv + aZe)],(11)

LBt = 4 (WM-W- - W-W—) .(12)

Полный лагранжиан электрослабой модели с преобразованием калибровочной группы и пространств полей вида (4), (6) равен сумме бозонного, лептонного и кваркового лагранжианов ^L EWM ⁽ ^ ) = ^L B ⁽ ^ ) + ^L L ⁽ ^ ) + ^L Q ⁽ ^ ) и записывается в виде разложения по степеням параметра ξ

L ewm ( € ) = L ( € ) + L^{m t} ( € ) =

— f f int . ^2 (f 1 fint ) 1 л4 fint

= ^L 0 + ^L 0 + ^€ ( ^L 2 + ^L 2 I + ^{€ L} 4 ,     ⁽²³⁾

где слагаемые г       г          г          Л

L 0	= L b, о	+ L L, 0 + l q, 0 ,
г int L 0	__ г int = l b, 0	1 г int + L L, 0	। г int + L Q, 0
L 2	= L b, 2	/4 + L L, 2	+ L Q, 2 ,
т int L 2	__ г int = L B, 2	1 г int + L L, 2	। г int + L Q, 2

L n = LB^            (24)

даются формулами (7)–(22).

При уменьшении температуры T ^ 0 , параметр £ = BT p ^ 0 , поэтому слагаемые с более высокими степенями ξ вносят меньший вклад в лагранжиан электрослабой модели по сравнению со слагаемыми с меньшими степенями, т. е. происходит изменение доли вкладов разных слагаемых в общий лагранжиан. Таким образом, по мере остывания Вселенной имеет место непрерывное перераспределение силы взаимодействий между входящими в электросла-бую модель элементарными частицами их вклада в формирование космической плазмы.

• 2.    Упругое рассеяние нейтрино

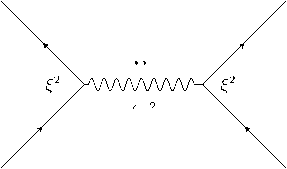
Чтобы прояснить физический смысл параметра деформации ξ, рассмотрим упругое рассеяние нейтрино на лептонах и кварках. На рис. 1, a) представлена диаграмма, описывающая взаимодействия нейтрино с электронами посредством заряженных токов с помощью обмена W -бозонами, а на рис. 1, b) — с помощью нейтральных токов путем обмена Z-бозонами. При подстановке преобразованных полей (6) обе вершины на диаграмме 1, a) умножаются на ξ2 , а пропагатор виртуального поля W умножается на ξ-2, поскольку пропагатор есть обратный оператор к оператору свободного поля, который для поля W умножается на ξ2. Для диаграммы на рис. 1, b) только одна вершина приобретает множитель ξ2, тогда как вторая вершина ν и пропагатор e

поля Z не изменяются.

W

ξ

ν

ν

ν

a)

b)

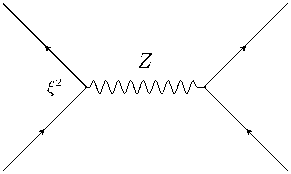
Рисунок 1. Упругое рассеяние нейтрино на лептонах.

Figure 1. Elastic scattering of neutrinos on leptons.

e

e

e

Таким образом, амплитуды вероятностей для заряженных и нейтральных слабых токов преобразуются одинаково M → ξ ² M . Сечение пропорционально квадрату амплитуды, следовательно, сечение упругого рассеяния нейтрино на лептонах при деформации (4) калибровочной группы умножается на ξ ⁴ . При энергиях нейтрино m _e ≪ E _ν ≪ m _W оно вносит основной вклад во взаимодействие нейтрино с лептонами и имеет вид [13, 14]

& vi = G F sf ( x ) ,                (25)

где G F = 1 , 17 • 10 - ⁵ ГэВ - ² есть константа Ферми, s – квадрат энергии столкновения в системе центра масс, f ( x ) - функция угла Вайнберга, x = sin d w . Принимая во внимание, что параметр ξ безразмерный, можно написать

° vi = £ ⁴ а 0 = ( G f s )( G f f ) ,          (26)

где а 0 - сечение рассеяния при £ = 1 , и получить выражение контракционного параметра через константу Ферми и энергию нейтрино в системе центра масс

£ ²( s ) = ^G^~s.                (27)

Диаграммы упругого рассеяния нейтрино на кварках посредством нейтральных и заряженных токов изображены на рис. 2. Они преобразуются аналогично диаграммам рис. 1. Сечения рассеяния нейтрино на кварках при энергиях m _e ≪ E _ν ≪ m _W имеют такой же вид (25) [13]

a vw = G F sf( x ) , a vz = G F sf( x ) .    (28)

Нуклоны представляют собой сложные образования из кварков, поэтому в выражении для сечения рассеяния нейтрино на нуклонах появляется формфактор avn = GF sF( x),              (29)

но оно по-прежнему преобразуется согласно (26). При энергиях m e ≪ E ν ≪ m W упругое рассеяние вносит основной вклад в общее сечение σ νm взаимодействия нейтрино с веществом, поэтому последнее при деформации калибровочной группы (4) ведет себя аналогично σ νl (25), (26).

eu

W

ξ ²                       ξ ²

_ξ - 2

νd

a)

νd

Z

ξ ²

νd

b)

Рисунок 2. Упругое рассеяние нейтрино на кварках.

• Figure 2. Elastic scattering of neutrinos on quarks.

В лабораторной системе отсчета сечение рассеяния σ νl (25) в интервале энергий m e ≪ E ν ≪ m W линейно зависит от энергии E ν падающего нейтрино [15]

a _vi ( E v ) = m e G F E v g,            (30)

где g - форм-фактор. При энергиях в середине интервала от me = 0,5 МэВ = 0,5 • 10-3 ГэВ = 0,5 • 106 эВ до mW = 80 ГэВ = 8 • 1010 эВ, т. е. до своего отщепления, нейтрино находится в термодинамическом равновесии с космической средой, поэтому энергия термализованного нейтрино совпадает с температурой Вселенной: Ev = T. В нашей модели деформация электрослабой модели начинается при температуре T0 = 102 ГэВ. При этой температуре параметр деформации равен единице £(T0) = 1, а сечение avl(T0) = а0. Заменяя в (30) энергию на температуру и учитывая (26), перепишем последнее выражение в виде avi (T ) = £ 4( T) а о = meGFTg, (31)

где а 0 = m _e G 2_F T 0 g . Тогда при T ниже 100 ГэВ из (31) получаем зависимость параметра деформации от температуры Вселенной

£ ⁴( T ) = T - ¹ T = T • (10 - 2 ГэВ - ¹) , (32)

где температура измеряется в ГэВ. В результате сечение рассеяния нейтрино на лептонах в указанных пределах линейно зависит от температуры avi (T ) = T—1 Ta о, (33)

что согласуется с имеющимися экспериментальными данными, представленными на рис. 3, взятом из работ [14, 15].

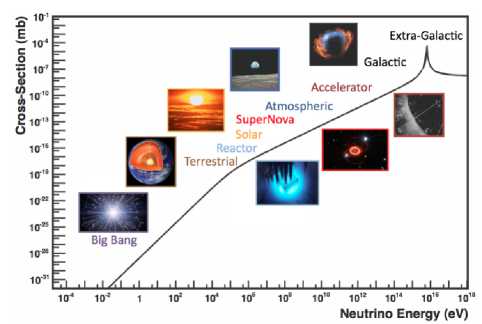
Рисунок 3. Электрослабое сечение для реакции vee  ^ vee рассея ния на электронах как функция энергии нейтрино.

Figure 3. Electroweak cross section for the reaction v e e - ^ v e e - scattering on electrons as a function of neutrino energy.

• 3.    Бета-распад

Важными реакциями с участием нейтрино являются радиоактивные превращения атомных ядер

A X ^— ZA+1 Y + ^e + ^V e ,          ⁽³⁴⁾

которые происходят за счет слабого взаимодействия путем превращения нейтрона в протон или эквивалентно

v e + n — p + e              (36)

и называются электронным или прямым β ^- -распадом [14].

Диаграмма Фейнмана прямого β ^- -распада (36) изображена на рис. 4. Один из двух d -кварков, входящих в состав нейтрона n , испуская W ^- -бозон, переходит в u -кварк. В результате оставшийся d -кварк и два u -кварка образуют протон p , а W ^- -бозон, взаимодействуя с электронным нейтрино ν e , порождает электрон e ^- . На диаграмме рис. 4 обозначены множители вершин и пропагатора, полученные согласно преобразованию полей (6).

p

d

u

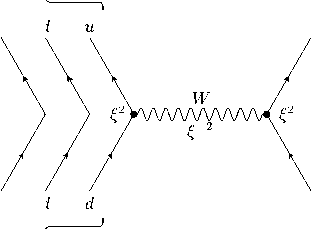
d

ν e

u

e

n

Рисунок 4. Диаграмма Фейнмана прямого β ^- -распада (36).

Figure 4. Feynman diagram of direct beta decay (36).

В системе центра масс сечение реакции (36) в приближении низких энергий me ≪ Eν ≪ mW выражается такой же формулой [13], как и в случае упругого рассеяния нейтрино a = GF sf, (37)

где s – энергия нейтрино в системе центра масс, G _F – константа Ферми, f – форм-фактор. Следовательно, и зависимость параметра деформации от энергии нейтрино такая же (27).

Другой тип β -превращений позитронный или обратный β ⁺ -распад

A X ^— ZA_— 1 Y ⁺ e ^{+ + V} e -          ⁽³⁸⁾

При X = p получаем в +-распад свободного протона p — n + e+ + ve,             (39)

который, однако, запрещен законом сохранения энергии, поскольку mp < mn + me. Действительно, mp = 938.27 МэВ, mn = 939.56 МэВ, me = 0.51 МэВ. Тем не менее процесс может происходить внутри ядра. Наконец, кβ-превращениям относятся процессы захвата нейтрино и антинейтрино ядрами с испусканием электрона и позитрона соответственно ve + A X —Z+1 Y + e ,         (40)

^V e + A X ^— _Z'‘ 1 Y + ^{e +} .            ⁽⁴¹⁾

Примером нейтринного захвата является реакция n — p + e + Ve             (35)

v + 37 Cl — — 38 Ar + e ,            (42)

предложеная Б. М. Понтекорво для регистрации солнечных нейтрино. Хлор-аргоновый метод Понтекорво был использован Р. Дэвисом в первом эксперименте по обнаружению солнечных нейтрино.

Нуклиды, подверженные β -превращениям, имеются буквально у каждого элемента начиная с Z = 0 (нейтрон) и до больших Z . В частности, при Z = 1 ,А =1 реакция (41) дает

ve + p ^ n + e+. (43)

Диаграмма Фейнмана обратного β ⁺ -распада (43) изображена на рис. 5.

n ud

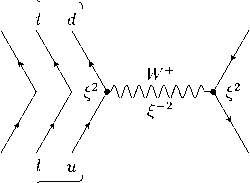
νe ud

e ⁺

p

Рисунок 5. Диаграмма Фейнмана обратного β ⁺ -распада (43).

Figure 5. Feynman diagram of inverse beta decay (43).

Один из двух u -кварков, входящих в состав протона p , испуская W ⁺ -бозон, переходит в d -кварк. В результате оставшийся u -кварк и два d -кварка образуют нейтрон n , а W ⁺ -бозон, взаимодействуя с электронным антинейтрино v _e , порождает позитрон e ⁺ . На диаграмме рис. 5 обозначены множители вершин и пропагатора, полученные согласно преобразованию полей (6). Сечение реакции находится аналогично сечению прямого в - -распада и совпадает с (37).

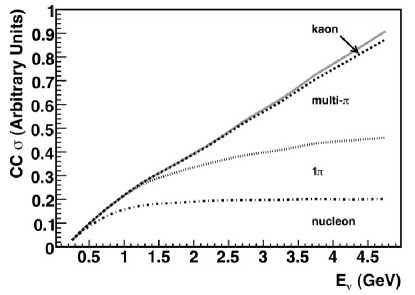
Рисунок 6. Предсказанные процессы для полного сечения инклюзивного рассеяния нейтрино на ядрах при промежуточных энергиях [15].

Figure 6. Predicted processes for the total cross section of inclusive neutrino scattering on nuclei at intermediate energies [15].

Полное сечение рассеяния нейтрино на ядрах, включая процессы прямого и обратного β -распадов, содержит вклады квазиупругих, резонансных и глубоконеупругих процессов. При промежуточных энергиях 1 ГэВ < E _v <  20 ГэВ оно демонстрирует линейную зависимость от энергии нейтрино по мере увеличения энергии нейтрино (рис. 6), а с учетом того, что энергия нейтрино совпадает с температурой (средней энергией) Вселенной E _v = T , линейно зависит от T , как и в случае упругого рассеяния (33).

Заключение

Деформация (4) или (5) калибровочной группы элек-трослабой модели приводит к перераспределению вклада различных слагаемых лагранжиана (23), т. е. к относительному усилению или ослаблению электрослабых взаимодействий между частицами и, следовательно, изменению их вклада в общее течение электрослабых процессов. Анализ преобразований фейнмановских диаграмм, описывающих упругое рассеяние нейтрино на лептонах и кварках, нахождение вида преобразования сечения рассеяния (31) в зависимости от температуры Вселенной и сравнение с теоретически вычисленным сечением позволили установить зависимость (32) параметра деформации от температуры £ ⁴( T ) = Т- ¹ T = T ■ (10 - ² ГэВ - 1 ), если температура измеряется в ГэВ. Верхний предел деформационного параметра £ ( T 0 ) = 1 достигается при T 0 = 10 2 ГэВ, связанной с характерной температурой электрослабого взаимодействия.

Рассмотрение более сложных процессов с участием нейтрино, таких как радиоактивные превращения атомных ядер, включая прямой (36) и обратный (43) β -распады, фейнмановские диаграммы которых изображены на рис. 4 и 5, несмотря на то, что многие факторы усложняют их простое описание, также демонстрирует линейную зависимость сечения реакций от энергии нейтрино [15], т. е. от температуры T (см. рис. 6).

Температура Вселенной в настоящее время совпадает с температурой реликтового излучения T = 2 , 7 ° K = 2 , 3 ■ 10 - ¹³ ГэВ ( 1 ° K = 8 , 6 ■ 10 — ¹⁴ ГэВ), что дает величину параметра деформации £ 2 (2 , 7 ° K ) ^ 5 ■ 10 - 8 . При характерной температуре сильного взаимодействия параметр деформации равен £ 2 (0 , 2 ГэВ ) ^ 5 ■ 10 - 3 .

Таким образом, деформации калибровочной группы (4), (5) соответствуют низкотемпературному пределу стандартной электрослабой модели и согласованы с экспериментально установленными фактами: слабым взаимодействием нейтрино с веществом, а также ростом сечения этого взаимодействия с увеличением энергии нейтрино.

Поскольку в электрослабой моделе калибровочная группа отвечает за взаимодействия между частицами модели, то ее деформация, связанная с уменьшением внедиагональных и соответствующим увеличением диагональных элементов, свидетельствует о перераспределении силы электрослабого взаимодействия между нейтрино, электроном, u - d -кварками при понижении температуры Вселенной от 100 GeV до температуры настоящего времени.