Некоторые аналогии в теории аналитических и гармонических функций

Интеграл Пуассона и формула Щварца.

Укажем аналогию между гармоническими и аналитическими функциями. Пользуясь связью гармонических функций с аналитическими, можно вывести аналогичные свойства гармонических функций из уже известных свойств аналитических функций.

Пусть и(х, у)  - однозначная функция,  гармоническая в некотором круге:/С: |z — z0| < R. Тогда  в круге   К существует однозначная гармоническая функция и(х,у) , сопряженная с и(х,у). Теперь образуем соответствующую аналитическую функцию  f(z~) = и(х, у) + iv(x, у) и разложим ее в ряд по степеням (z — z0): f(z) = Z№n + iPn)(z — z.)', где a^Pn ER.                        (1)

Введем полярные координаты г и 9 с полюсом в точке z0, так что z = z0 + те19 и обозначим и(х,у) через и(г, 9), а v(x, у) через ^(г, 9) в качестве разнозначащих функций. Отделяя мнимые и действительные части, получим ряды:

и(г, 9) = а0 + ^(a^cos п9 — pn sin п9)гп,

г(г, 9) = /?₀ + ^ ” (/?_ncosn9 + a_n sin п9)г^п . (3) Равномерно сходящиеся внутри К.

Таким образом, каждая функция и(г, 9), гармоническая внутри круга |z — z₀| < R, допускает в нем разложение вида (2), равномерно сходящееся внутри этого круга, где а_п и P_n е R. Так как степенной ряд (1) сходится в данном круге и возможно имеет радиус сходимости больше чем R, то число это должно удовлетворять неравенству:

R ^------ 1

.

lim V|«n + ^n| n^to

Если ссп и (Зп - заданные числа, удовлетворяющие последнему неравенству, то ряд (2) определяет функцию, гармоническую внутри круга K. Наличие разложения вида (2) или (3) с соответствующим неравенством, наложенным на коэффициенты ряда, является характеристическим признаком функций гармонических внутри данного круга.

Применим разложение (2) или (3) к гармоническим функциям на примере функции /(z) =

peia+(z-z0)

pe^to-(z-z₀) ^.

peia+(z-z0)

Так как для функции /(z) = ^^   ^ разложение в круге |z —z0| < p примет вид:

pe^ia + (z — z₀) pe^^a — (z — z o )

1+ У" = —1 + 2[1+^ + <^ 0^{) 2}

pi a (z- z₀)                 pe^ia     p²e^2ia

to

то

Re[/(z)] =

= —1 + 2

О — z o ⁾ⁿ

pn

e -ma

p²-r² p 2 +r²-2rpcos(6-a)

n

1 + 2 5 ” —cos(0 — a),

2rpsin(0-a) p²+r 2 -2rpcos(6-a)

n

2 5 ” —sinn(0 — a) .

Причем оба ряда равномерно сходятся внутри круга |z — z0| < p. Возвращаясь к рядам (2) и (3), перепишем первый из них, заменив г через произвольное p(p < R) и - через a , затем умножим обе части на cosma и проинтегрируем (при фиксированном p) по a в пределах от 0 до 2л\

Получим JQ27r u(p, a) cos a da = ampm /2я cos2 mada .

Откуда a0 = ^ /02я u(p, a)da и am = ~^ ^2Я u(p, a) cos mada , m > 1.

Аналогично, умножая на sin ma и интегрируя в тех же пределах найдем: —Pm = z^7^)27ru(p, a) sin mada , m > 1 .

Поставляя найденные выражения для a^ Pn в ряды (3.2) и (3.3) будем иметь 1 2^            1 ^

н(г, 0)=—I u(p, a)da + —у u(p, a) cosm(0 + a)da * —, 2u J            nZ-ip та   2к                            ^

ц(г, 0) = /?₀ + ^ — J и(р, и) sinm(0 — a)da * —.

^" 0                  ^р ~

Пусть р такое, что г < р < R. Очевидно, последние выражения могут быть получены из формул (4) и (5) путем умножения на ~и(р, а) и полученного интегрирования по а в пределах от 0 до 2и (при фиксированных г и р). Все эти операции законны в силу равномерной сходимости рядов (4) и (5) внутри круга |z — z0| < р. Итак получим:

2к                   та гП

—- cos р^П

п(0, а)] da

^u(r,0)=^j и(р,а)11 + 2^

2к

1                       р2 — г2

^и(г'⁰⁾⁺2и\ ^u(р,^a)da? 2 +^ 2 —2р7■o(ёa)^da'   ⁽⁸⁾

2к              та гП

— sinn рП

(0, а)] da

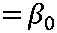
^(г, 0) = ^0 + ^ J и(р, а) М^

2к

1                2грsin(0, а)

⁺ 2л] ^и(р,^а) р² + г² — 2рг cos(0, а) ^^а.

Таким образом, для функции и(г, 0)и сопряженной с ней функции ^(г, 0)

выявлены интегральные представления через значения и(г, а) в точках окружности |z — z₀| < р (< R).

Различия интегралов в (8) и (9) объясняются тем, что во второй из них гармоническая функция п(г, 0) выражается не через свои собственные значения на окружности |z — z0| < р, а через значения сопряженной с ней функции. Однако формула (8), установленная для любой гармонической в данном круге функции, справедлива также и для v(x, у). Поэтому для ц(г, 0) имеем формулу, аналогичную формуле для и(г, 0):

р(г, 0) = — Г 2 ^к ц(р, а) ——-^—-———- da .                     (10)

2к 0           р²+- 2 -2р-cos(0,a)                                    ^{v 7}

Интеграл, стоящий в правой части формулы (8) или (10) называется интегралом Пуассона соответствующий функции и(p,a) или ■v(p,a), p²-r²               pe^ia+(z-z )

гармоническая функция        p2+r2-2prcos(6,a) = Re lpe

По формуле (3) и(г, 9) = 1, получим:

1 = — Г²"

2" 0

p2-r2 p2+r2-2pr cos(6,a)

da.

Если ф(a') - действительная функция, определенная и непрерывная на сегменте [0; 2я], то интегралом Пуассона называется выражение вида:

- С Ф(a) _{2 2}^p2-r2 „ . da.               (12)

2к 0         p²+r²-2pr cos(6,a)                         ^{v 7}

Не требуя, чтобы функция ф(a) совпадала со значениями некоторой гармонической функции и(р, a) (12) представляет гармоническую функцию в круге \z — z0\ < р, которая при приближении точки (г, 9) к какой- либо точке (р, a) стремится к пределу, равному ф(a). Интеграл Пуассона аналогичен интегралу Коши, распространенному на окружность, и может быть получен некоторыми преобразованиями из последнего интеграла. С этой целью рассмотрим наряду с формулой Коши:

^J(Z)   2"^j\^-z₀\=p^-z*

df,

где точка z лежит внутри окружности |f — z0| = р, интеграл Коши, p2

полученный путем замены z точкой z = z0 + ^= , симметричной с z z-Zo относительно окружности |f —z0|=p. Так как точка z* лежит вне окружности, то этот интеграл должен равняться нулю:

-^_f,  T^.d^.

(13*)

2" \^-zo\=p ^-z*

Вычтем почленно (13*) и (13) и преобразуем результат, воспользовавшись тем, что:

^ — z = ^ — z₀ — (z — z₀) = ре^1а — ге¹⁶ ,

^ — z* = f — z₀ — (z* — z₀) = ре¹“ — р~ e^t6 , г

Найдем

df = ipeiada.

^f(z)=^ / ^f(^-r^-

|^-zo|=P

1 Г       Г      p            rei(a—e)

] da =

2л        p — rei(9-a) p — re1^-6)

2я

1 Г               p2 — r2

2л j ^(^) p² + r² — 2rp cos(a — 0) ^^a .

Получили таким образом интегральную формулу Пуассона для аналитической функции f(z) Заменяя здесь f(z) на u(r, O') + iv(r, O'), а f(f)

на u(p,a) + iv(p,a) и отделяя действительные и мнимые части, вновь получаться формулы (3) и (5).

Из формул (8) и (9) легко выводится важная формула, выражающая аналитическую функцию f(z) через значения ее действительной части на окружности. А именно умножая (9) на i и складывая с (8) получится:

2я

1                     p2 — r2

^f(z) = ^ ⁺ - ^j “^(p,^a) [p2 + r2 — 2rpcos(0 — a)

2prsin(0 — a)

^{+ i} т ; т          ¹            г ^da.

p2 + r2 — 2rpcos(0 — a)]

Но выражения в квадратных скобках представляют собой аналитическую peia+(z-z0)

функцию ^{от z:}_pei_a-(z-zo). Поэтому

f(z) = ip₀ + 1- £2^Л_u(p, a) ^{pe +(z z}0) da . ⁰2я 0           pe^ia-(z-z0)

Формула (15) носит название формулы Шварца.

Здесь i/₀- чисто мнимая постоянная, представляющая мнимую часть значения f(z₀); эта постоянная не может быть определена по действительной части функции f(z').

Из формулы (8) при r = 0, то есть для центра круга К = {z:\z — z0| < й} где и(р, а) обозначает функцию и(х,y) в точках окружности |z — z0| = р с центром в точке z0 = х0 + iy0 при более подробной записи будем иметь:

и(х₀ + iy₀) = ^/₀2^Яи(х₀ + р cos a,y₀ + р sin a)da .          (16)

Следовательно, значение гармонической функции в центре окружности равно среднему значению ее значений по окружности с центром в этой точке. Эта особенность является функцией признаком особенностей гармонических функций, точнее, следующее утверждение является правильным: Утверждение: пусть и(х,y)- действительная функция, однозначная и непрерывная в области G. Если для каждой точки z₀ = х₀ + iy₀ £ G существует окрестность |z —z₀|<5(z₀), в которой и(х₀ + iy₀) равна среднему арифметическому своих значений по любой окружности |z — z₀| = р, 0 < р < 5(z0) ,то и(х + y) является гармонической функцией в области G.

Кроме того, гармонические функции, а также аналитические функции:

• 1)    разлагаются в степенной ряд по степеням |z — z₀|;

• 2)    бесконечно дифференцируемы;

• 3)    Значения гармонических и аналитических функций равны среднему значению их значений на окружности с центром в этой точке.