Некоторые асимптотические разложения компонент тензора Эшелби в случае кубической и гексагональной анизотропии

Задача об искажениях, вносимых в поле напряжений включениями - областями, претерпевшими изменения формы и линейных размеров, или неоднородностями, которые характеризуются иными значениями упругих констант, чем в остальном материале, - имеет глубокие корни в механике. Одним из основных методов решения задач данного типа является метод Эшелби [1], в основе которого лежит задача нахождения связи компонент стесненной ( в_ц ) и свободной от напряжения деформации ( в ^c _kl ) во включении. В случае эллипсоидальной формы включения напряжения внутри него однородны и искомая связь осуществляется с помощью компонент тензора Эшелби S_ijkl [1]:

^£ j = S ijkl ^в ki •

Для изотропного тела компоненты тензора Эшелби для включения в форме произвольного трехосного эллипсоида с полуосями а1, a2, а3 выражаются через эллиптические интегралы, для включения в форме эллипсоида вращения - через элементарные функции [1, 2]. Наиболее простой вид компоненты тензора Эшелби приобретают для включений в форме частных видов эллипсоидов вращения: шарообразного, дискообразного, игольчатого.

Классический подход Эшелби обобщается для случая произвольного анизотропного материала, однако компоненты тензора Эшелби при этом не могут быть посчитаны в замкнутом виде и сводятся лишь к комбинации некоторых поверхностных интегралов, которые путем параметризации сводятся к обыкновенным либо двукратным. Решение в замкнутой форме получено лишь для частного случая включений в трансверсально-изотропной среде [3].

В данной работе предложен способ подсчета компонент тензора Эшелби в случае сфероидальной неоднородности в среде, обладающей кубической и гексагональной анизотропией, с помощью разложения по малому параметру, характеризующему отклонение тензора упругости кристалла от изотропного тела или трансверсально-изотропного кристалла специального вида (соответственно для кубического и гексагонального кристаллов). Результаты, полученные описанным методом, сравниваются с результатами численного интегрирования. Рассматриваются сферические, дискообразные и игольчатые включения.

Хотя численное вычисление интегралов, через которые выражаются компоненты тензора Эшелби для анизотропных кристаллов общего вида, не представляет принципиальных трудностей, оно все же требует значительного числа операций, что весьма затрудняет анализ зависимостей компонент тензора Эшелби от упругих параметров матрицы и геометрии включения. С учетом того, что при вычислении энергии включения, эффективных упругих характеристик тел со включениями, концентрации напряжений внутри включения и на его контуре [2] выражения для компонент тензора Эшелби входят в громоздкие алгебраические выражения, анализ зависимостей данных величин от упругих и геометрических параметров становится еще более сложной задачей. В этой связи наличие асимптотических формул типа полученных в настоящей работе представляется весьма полезным.

2.    Асимптотическое разложение компонент тензора Эшелби для кубического кристалла

Тензор Эшелби для случая кубического кристалла может быть посчитан через компоненты вспомогательного тензора G ipjq [2]:

S..., = C (GG . + G. . ). yki       pqki ipjq jpiq

(1.1)

G11n = G2222 = — (1—x)(1 -x2 + r2x2)[ц2(1 -x2 + r2x2) + Pr2x2]dx + a 0 pq

+ Л Г--x ) [p(1 - x2 + r 2x2 ) + уr2x2 ]dx, a 0 p (p + q)

G3333 = — fr x (1 - x2 + r2x2)[ц2(1 - x2 + r2x2) + P(1 - x2)]dx + a 0 pq

• 1  22      2x2

+ лу r r x (1 - x ) dx a 0 p(p+q) ’

G1122 = G2211 = —   ——{(1 - x2 + r2x2)[ц2(1 - x2 + r2x2) + Pr2x2]dx + a 0 pq

+ (1 - x ²)[ P (1 - x ² + r²x ²) + у r²x ²]} dx -Л [^{(1 - x 2)2 [} P ^{(1 - x 2 + r 2 x 2) + y r 2 x 2] dx} , a 0             p ⁽ p ⁺ q )

G1133 = G2233 = — r-x- {2(1 - x2 + r2 x 2)[ц 2(1 - x2 + r2 x2) + P r2 x2] + a 0 pq

+ (1 - x ² )[ P (1 - x ² + r ² x ²) + y r ² x ² ]} dx ,

G \₂\₂ = - ^{Л (}^ ⁺ ^ ) ~—x ) [ ц (1 - x ² + r ² x ²) + Ц 1 r ² x ²] dx ,     (1.2)

a 0 p ⁽ p ⁺ q )

G1313 = G2323 =- 2л^Х + ^ r_x_(1 -x2)(1 -x2 + r2x2)dx- a 0 pq лц^Х + ц) Vr2x2(1 -x2)2dx a 0 p (p+ q) ’

G33n = G3322 = — f(1 -x )(1 -x2 + r2x2)[ц2(1 -x2 + r2x2) + P(1 -x2)]dx + a 0 pq

+ лу V(1 - x ²)³ dx

• ²    a 0 p ⁽ p ⁺ q ) ’

где

a = ц2(Х + 2ц + ц1), b = a 1цц|(2л + 2ц + ц1),c = а-1ц2(3Х + 3ц + ц1), у = Ц1(2Х + 2ц + ц1),

p = { (1 - x ² + r ² x ² ) ³ + br ² x ² (1 - x ² )(1 - x ² + r ² x ² ) +

1/2

(1 - x ² ) ² [ b (1 - x ² + r ² x ² ) + cr ² x ² В   , 0 <  x <  1,

1 + 4

q = {(1 - x ² + r ² x ² ) ³ + br ² x ² (1 - x ² )(1 - x ² + r ² x ² )} ^1/2 , 0 <  x <  1. С - тензор упругости; для кубического кристалла он имеет вид

Ck = X5 ] 5 н + р(5ж 5 , +5, 5jk) + ц,5 „ 5jk.            (1.3)

Случай ц 1 = 0 соответствует изотропному телу, при этом X и ц соответствуют константам Ламе изотропного тела.

Сделав в формуле (1.3) замену

Ц 1 =ец ,                             (1.4)

будем раскладывать получившееся выражение в ряд по степеням параметра £ , характеризующего отклонение от изотропного случая.

Рассмотрим подробнее некоторые частные случаи для включения в форме сфероида с полуосями а 1 = а ₂ и а ₃. Для r = 1/ р = а 1 / а ₃ <  1 имеем вытянутый сфероид, для r >  1 - сплюснутый, для r = 1 - сферу.

2.1.    Асимптотическое разложение для сферического включения

Сделав в выражении (1.3) замену (1.4), разложим его в ряд по степеням £ :

с _с(0) ,Ре(1)    2е(2) ,

IjH      i]kl ^{+ £} ]kl ^{+ £} i]kl ⁺ •••

Первый член, очевидно, соответствует изотропному телу, следующие члены дают соответствующие поправки.

Подставляя р = 1, что соответствует сферическому включению, в выражение (1.2), получаем при разложении в ряд этого выражения следующие независимые компоненты тензора Эшелби:

с⁽⁰⁾ — е(⁰) _ е(⁰) _ ^{7 5 v}

1111 = °2222 = 3333 = , х,

15(1 -v )

• У ^{( 0 )} = У^{(0 )} = У^{(0 )} =У^{(0 )} =У^{(0 )} =У^{( 0)} =--^{1 - 5 v}

  1122      1133      2211      2233      3311      3322       . -_Zl х>

15(1 -v )

У⁽⁰⁾ =у⁽⁰⁾ =у^{(0 )} = ^{4 - 5 v} 1212      1313 ^а2323                х,

15(1 -v )

• У⁽¹⁾ = У⁽¹⁾ =У⁽¹⁾ =-7У⁽¹⁾ =-7У⁽¹⁾ =-7У⁽¹⁾ = ^{17 - 48 v + 42 v}

  1111     2222     3333 ^Z'*^J2323 ^Z'*^J1313     ^Z'*^J1212       01^/1             ’

315(1 - v )

с (1) _ с^{( 1)} _ с⁽¹⁾  _ с⁽¹⁾ _ с⁽¹⁾ _ с⁽¹⁾

1122 = 1133 =   2211 = 2233 = 3311 = 3322

2 - 39 v + 63 y 2 315(1 -v ) ²

V(2) - <'2) - <'2) -К2) -К2) -К2) =

1111     2222     3333     ^°2323     ^°1313     ^°1212

_ 971 - 4134 v + 7436 v ² - 5148 v ³

=           90 090(1 -у)3,

V(2) - V': = V(2) - <'': - <'':     <'2) =

1122      1133      2211      2233      33113322

_- 15 - 4225 v + 14586 v ² - 12870 v ³

=           90 090(1 -v)3

Под v здесь понимается величина у = 91/121 + 8ц, соответст вующая коэффициенту Пуассона изотропного тела (ц1 = 0). Получен ные разложения и результаты численного интегрирования представлены на рис. 1. На графиках сплошные линии соответствуют численному интегрированию, пунктирные линии - разложению при учете линейных по в членов, штрихпунктирные - при учете квадратичных. Расчеты проводились для у = 0,25, что соответствует 1 = ц.

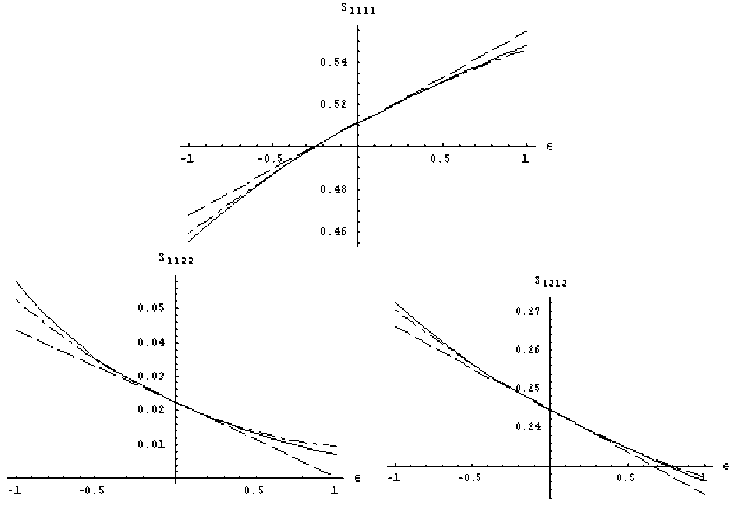
Рис. 1. Расчет компонент тензора Эшелби для сферического включения в кубическом кристалле

2.2.    Асимптотическое разложение для дискообразного включения

Если рассматривать предел бесконечно тонких включений р ^ 0, большинство компонент тензора Эшелби обнуляется. Для приложений, однако, полезно иметь следующие члены разложения. В отличие от предыдущего примера ситуация осложняется наличием двух малых параметров в и р, и разложение можно выписать в форме

S-kI = S У + S У⁶ + S ⁽« ^ + S ⁽ k;^{2 ) e} 2 + S ^Р ⁸ + S 50V + - (1.5) ijkl ijkl ijkl ijkl ijkl ijkl ijkl ^{... .}

Заметим, что наличие двух малых параметров вовсе не предполагает одинаковость порядка их малости, и мы, в принципе, вправе удерживать различное число членов разложения по каждому из этих параметров. Однако результат подобных разложений нуждается в обосновании; для рассматриваемого случая оно будет выполнено после получения результатов.

Разложение выражения (1.1) по степеням р интегрируется по x лишь для членов, не содержащих р, причем для произвольных значений в. Для ненулевых членов

с(М _ с⁽М _------- 2 1------- е^(0,в) _ 7 е(^0,в) _ р е^(0,в)

3311      3322           п                      3333 ^Z'*^J1313 ^Z'*^J2323       ,        ⁽ - )

2 - 2v + b- 2v£ что для в = 0 соответствует хорошо известным выражениям. В выражениях (1.9) второй верхний индекс в указывает на то, что данные выражения не являются разложениями по в.

Для линейных по р и старших членов соответствующее выражение уже не интегрируется. Однако легко интегрируется почленное (по в) разложение (1.1). Получаемые при этом выражения, хотя и содержат лишь элементарные функции, достаточно громоздки. Ненулевые компоненты их разложения по р имеют вид:

с ( 1,k ) _ с(1,0 ) _ 1111 _ 2222 _	л ( 13-	- 8 v )	V(1 , k) _ C(1 , k) _ 1122 _   2211 _	л (1 - 8 v )
	32(1	-v ) ,		32(1 - v ) ,
с(1 , 0) _ с(1 , 0) _ 1133 _ 3311 _	л (1-	- 2 v )	V(1 , k) _ C(1 , k) _ 3311 _ 3322 _	л (1 + 4 v )
	8(1	-v ) ’		8(1 -v ) ’
S (1,0) _ т (1 - 2 v )	О( 1,0 ) 2323	— C ( 1,k ) _ 1313	л (2 - v )	S ( 1,0 ) _ ^(7 -	- 8 v )
3333        4(1 - v ) ,			8(1 - v ) ,	1212     32(1	-v )

С(1,1) _ сО^ _

1111 ^_ 2222 ^_

л [ 425 - 16 v (53 - 40 v ) ]

с⁽¹1 _ сМ _ 3311     3322

4096(1 — v ) ²

л [5 + 128v(1 - 3v)]

512(1 - v ) ²

,

S (ц) _ л (9 - 50 v + 64 v ² )     S (_W)

³³³³        2 5 6(1 — v ) ^{2     ,     2323}

S _{(u) =} S _(1Д) _ л [ 1 + 16v(5- ² 4 v ) ] ^{1122 2211}          4096(1 -v ) ² ,

S (i,i) _ S (i,i) _ ^{л (5 - 34 v + 48 v 2) 1133 2233}         5 1 2(1 - v ) ²      ,

_ S (i,i) _   л (27 - 68 v + 64 v ² )

¹³¹³           512(1 -v ) ²      ,

S _(u) _ л [ 65 - 32 v (5 - 4 v ) ] ¹²¹²          4096(1 - v ) ² ,

S(1,2) _ S(1,2) _ л(5345 -9792v + 12544v2 - 18 432v3) 1111 _ 2222 _               524 288(1 - v)3

S(1,2) _ S(1,2) _ л(333- 1680v -15104v2 + 30 720v3) 1122 _ 2211 _             524 288(1 - v)3

S(1,2) _ S(1,2) _ л(105-2598v + 8608v2 -7680v3) 1133 _ 2233 _             131072(1 - v)3

C(1,2) _ C(1,2) _ _ 3311      3322

л (105 + 18128 v - 99 840 v ² + 122 880 v ³ )

131072(1 — v ) ³

,

л (569 - 5550 v + 14 976 v ² - 122 880 v ³ )

S (1,2) _

³³³³                    65 536(1 - v ) ³              ’

S (1,2) _ S (1,2) _ л (727 - 3212 v + 7872 v ² - 7680 v ³ )

^{2323     1313}                131 072(1 - v ) ³

^^^^^^^в

,

S _{( 1>2} ) _ л (1805 - 6296 v + 9472 v ² - 6144 v ³ )

.

^{1212 _}            524 288(1 - v ) ³

Полученное разложение отличается по форме от (1.5) и записывается в виде

S ijki = S k ^Е) + S ^’p + S ^te + S ^’pe ² + ... + S jl ^{0 )} P ² + ...      (1.7)

Выражение (1.5) получается отсюда разложением первого члена по в и перегруппировкой.

Как отмечалось, наличие двух малых параметров в и р не предполагает одинаковость порядка их малости. Оставление большего числа членов разложения по одному из параметров (в в нашем случае) является оправданным в случае, когда он много больше другого, т.е. в >> р . Действительно, полагая

P = £ k,

подстановкой данного выражения в (1.5) убеждаемся, что удерживание членов вида S ^{( 1,1 )} и отбрасывание членов S ^{( 2,0 )} оправданно при 1 <  к <  2:

е _ е(°>^Е) , е(1,°)р ^к  , сО^ф ^{к +1}  । с⁽¹,²⁾_Р ^{к +2} _i_ С⁽²,⁰⁾_р^{2 к}

S ijkl ^S ijkl ^{+ S}ijkl ^{£  + S}ijkl ^{£    + S}ijkl ^{£    +} ••• ^{+ S}ijkl ^{£   +} •••,      О^⁸)

1 < к < 2^ 2 < к < 3

нижней скобкой отмечены удерживаемые члены^ Удерживание членов вида S ^{( 1,2 )} и отбрасывание членов S (^{2,0 )} становится оправданно при 2 <  к <  3 • Для того чтобы получаемые разложения оставались асимптотически верными, необходимо удерживать члены, содержащие S ^{( 1,3 )} при 3 <  к <  4 и т,д,, и, кроме того, формально, следуя процедуре, намеченной (1^5), следовало бы разложить выражение (1^6) в ряд по степеням £ и удерживать определенное число членов^ Однако данное действие не представляется рациональным ввиду простоты получившегося выражения: более целесообразным видится оставить выражение (1^6) в полученном виде, который, хоть и содержит избыточные с точки зрения асимптотического разложения члены, более прост Данные рассуждения относится также к случаям сильно вытянутых включений и включений в трансверсально-изотропной среде, рассматриваемым ниже^

Полученные разложения и результаты численных расчетов для компонент тензора Эшелби представлены на рис 2 (для v = 0,25, p = 0,01 )• Сплошные линии соответствуют численному интегрированию, пунктирные линии - разложению при учете линейных по £ членов, штрихпунктирные - при учете квадратичных^

В отличие от случая шарообразных включений, здесь наблюдается систематическое отклонение асимптотического решения от точного для всего рассматриваемого диапазона параметра малости, в том числе для нулевого значения^ Данное отклонение связано с тем, что рассматриваемое решение является двойным разложением: по £ и по р, те^ даже для £ = 0 рассматриваемое решение есть лишь главный член разложения точного решения по р^ Данное отклонение пренебрежимо мало для компоненты S ₃₃₁₁, для которой существует ненулевой член разложения по р (1.6)•

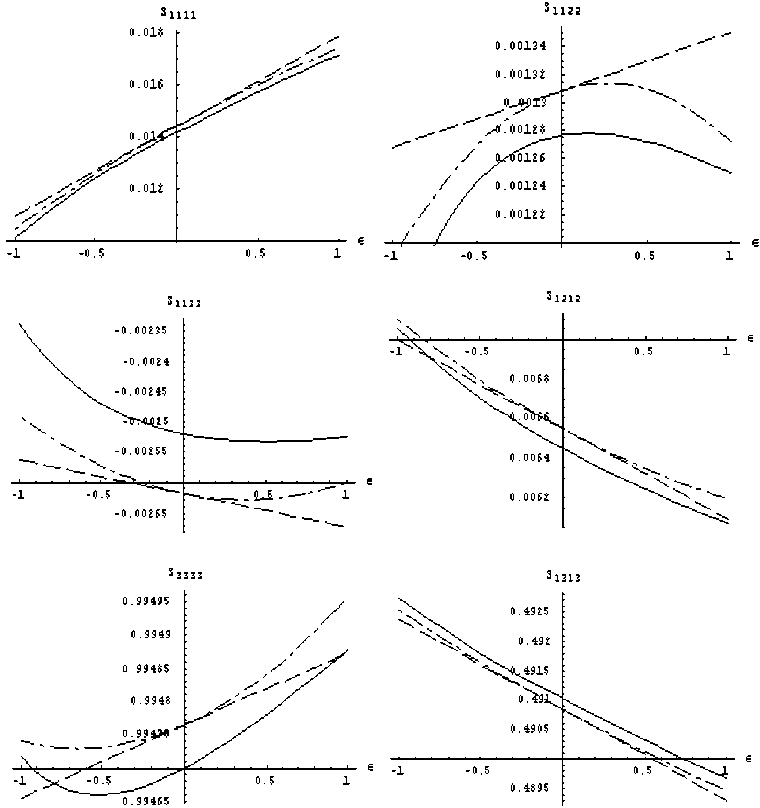
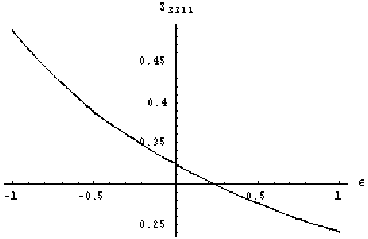
Рис. 2. Расчет компонент тензора Эшелби для дискообразного включения в кубическом кристалле

2.3.    Асимптотическое разложение для игольчатого включения

Данный случай соответствует r ^ 0. Разложим, аналогично предыдущему пункту, выражение (1.1) в ряд по степеням r . Для членов, не содержащих r , интегрирование по x выполняется элементарно в замкнутом виде для произвольных значений а. Для ненулевых членов е(0.8) _ <-,(0,8) _ ^{— 2} + Y~ ( 1 -y ) s , (0,_Е) _ ^(o.s) _ 4 + £- 2 y ( l -v ) -2v ( 2 + £ ) S 1111     S 2222                            ; S 1122 S 2211         ~            \      ( л \     ⁹

Y8                           2 v8 ( 2 + 8 ) -8 ( 4 + 8 )

e ( 0, 8 ) _ 0( 0, 8 ) _          2 v ( 2 ⁺ Y ^{+ 8)}         ,

S ¹¹³³ S ²²³³ _Y ( 2 + 8 ) [ 2 + 8- 2 v ( 1 + 8 ) ] ’

S _(M = 2±I^+8-2v(2 + Y + 2£)_

¹²¹²    ( 2 + y ) [ 4 + 8- 2 v ( 2 + 8 ) ] ’

c(0,E) _ c(0,e) 1313       2323         , где

Y =

( 2 + 8 ) 4 + 8- 2 v ( 2 + 8 )

2 + 8 — 2 v ( 1 + 8 )

что для 8 = 0 соответствует хорошо известным выражениям.

Для старших членов соответствующее выражение уже не интегрируется. Однако легко интегрируется почленное (по а) разложение (1.1). Получаемые при этом выражения, хотя и содержат лишь элементарные функции, достаточно громоздки. Ненулевые компоненты их разложе ния по r имеют вид:

с ( ^2,0)² _ е(^2,0 )² 1111 ' = 2222 '

С(^2,0L2 _ e(²’⁰)_r2 1122 *         2211 '

1 — 8 v + 4(1 — 2 v )ln r /2 ₂

r

16(1 — v )

5 — 8 v + 4(1 — 2 v )ln r /2 ₂

r

16(1 —v )

C^(2,0L² _ C^(2,0)_r 1133 '        2233 '

3 + 2 v + 2(1 + v ) In r /2 ₂ =------------------------ r ,

4(1 — v )

(1.9)

e( ^2,0 )Д _ e(²’⁰ ) Д °3311 ' ^,a3322 '

3 — 4 v + 2(1 — 2 v )ln r /2 ₂

r

4(1 — v )

e ( ^2,0 )_r 2 _ e(²’⁰ ) ° 1313 '       2323

₂ 2 + v + (1 + v )ln r /2 ₂

r =--------------- —r ,

4(1 — v )

S

( ^2,0L² _

1212 ' =

3 — 8 v + 4(1 — 2 v )ln r /2 ₂

r

16(1 — v )

С ( ^2,1 ) _г2 _ с( ^2,1 ) _г2 __ 1111 ^{r —} 2222 ^{r —}

103 - 372 v + 336 v ² + 24(3 - 10 v + 8 v ² )ln rj 2

5 ⁽2,1V ² = £⁽ 2,1V ² = 1122 ^r 2211 ^r

768(1 - v ) ²

95 - 3 84 v + 720 v ² + 24(3 - 14 v + 24 v ² )ln r /2

2 r ,

5 ^V² = s^V ² = 1133 ^r 2233 ^r

768(1 - v ) ²

35 + 15 v + 180 v ² + 12(1 -v + 12 v ² )ln r /2

2 r ,

s ⁽²’1v² = 5⁽²’1V² = 3311 ^r 3322 ^r

192(1 - v ) ²

35 - 168 v + 96 v ² + 12(1 - 4 v ) In r /2

2 r ,

192(1 - v ) ²

2 r ,

5 ^(2д)г² = -

3333 ^r

182 - 261 v + 144 v ² + 12(8 - 13 v + 8 v ² )ln r /2

96(1 - v ) ²

2 r ,

s (²’1V² = s^V² 1313 ^r 2323 ^r

107 - 186 v + 144 v ² + 12(5 - 10 v + 4 v ² )ln r / 2

S ^(2Д)Г² = -

1212 ^r

192(1 - v ) ²

25 - 72 v + 240 v ² + 24(1 - 4 v + 8 v ² )ln r /2

2 r ,

768(1 - v ) ²

2 r ,

где S j ^{,0 )} соответствуют членам разложения компонент тензора Эшел-би изотропного тела; выражения S j ^ не представлены ввиду их громоздкости.

В выражениях (1.9) и аналогичных выражениях, получаемых ниже, удержаны как члены с логарифмами r , так и без них.

Поскольку полученное разложение не содержит нечетных степеней по r, оно записывается для данного случая в виде s,ki = Sj;■’+Sjf'r2+Sijki"r■+sj;21 rv+...+Sir1+... (1.10)

Полагая r = ■ ^k в формуле (1.10), убеждаемся, что удерживание членов вида S (^2,1) и отбрасывание членов S (^4,0) оправданно при 1/2 <  k <  1:

с _ с ( 0, ^ ) , с(²’⁰)_Р^{2 k} , с(2,1)р^{2 k + 1} . е(²,²)р^{2 k + 2} _i_    _i_ с(⁴,0)р^{4 k} 1

S ijki S ijki ⁺ S ijki ■ ⁺ S ijki ■      ⁺ S ijki ■      ⁺ ••• ⁺ S ijki ■ ⁺ •••

1/2 < k < 1

4________________________________________v-                                      V

1 < k < 3/2

Нижней скобкой отмечены удерживаемые члены. Удерживание членов вида S ^{( 2,2 )} и отбрасывание членов S ^{( 4,0 )} становится оправданно при 1 <  к <  3(2. Остальные замечания, сделанные для случая дискообразных включений, остаются справедливыми и для данного случая.

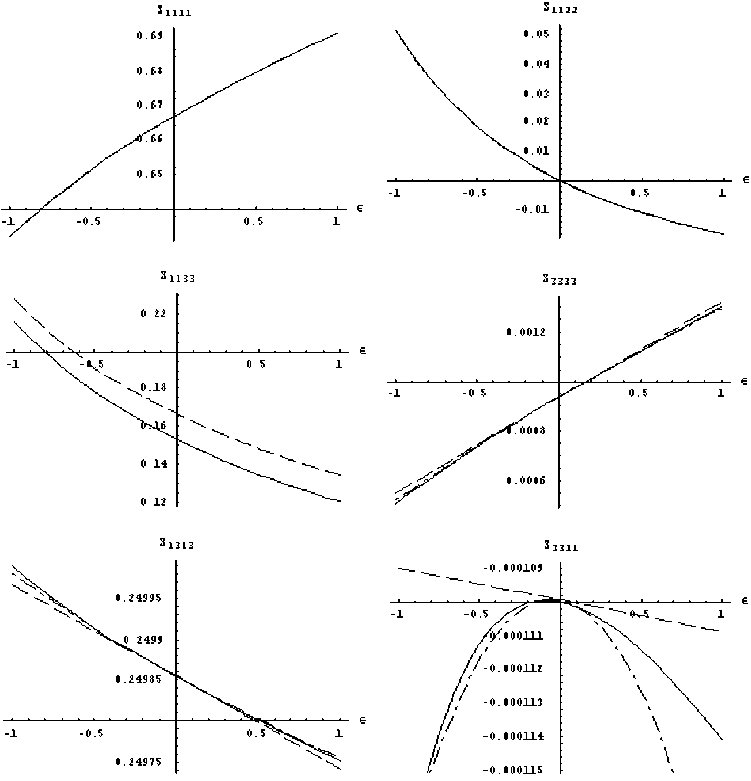
Рис. 3. Расчет компонент тензора Эшелби для игольчатого включения в кубическом кристалле

Полученные разложения и результаты численных расчетов для компонент тензора Эшелби представлены на рис. 3 (для v = 0,25, р = 0,01). Сплошные линии соответствуют численному интегрированию, пунктирные линии - разложению при учете линейных по £ членов, штрихпунктирные - при учете квадратичных. Подобно случаю дискообразных включений, здесь наблюдается систематическое отклонение асимптотического решения от точного для всего рассматриваемого диапазона параметра малости, в том числе для нулевого значения. Данное отклонение особенно заметно для компонент, не содержащих нулевого члена разложения по r .

3.    Асимптотическое разложение компонент тензора Эшелби в случае гексагональной анизотропии

Для гексагонального кристалла (трансверсально-изотропного тела) выражения для компонент тензора G ipjq , через которые выражается тензор Эшелби, имеют вид [2]:

G 1111 = G 2222 = -^ J a (1 - x ²){[ f (1 - x ²) + hr² x ²] x ²  0

x [(3 e + d )(1 - x ² ) + 4 fr ² x ² ] - g ² r ² x ² (1 - x ² )} dx ,

G ₃₃₃₃ = 4 л J A r² x ²[ d (1 - x ²) + fr² x ²][ e (1 - x ²) + fr² x ²] dx ,

Gm 2 = G ,2,1 = - ™ J a (1 - x ’){[. f (1 - x ²) + hr ² x ²] x ²0

x [( e + 3 d )(1 - x ²) + 4 fr ² x ² ] - 3 g ² r ² x ² (1 - x ² )} dx , G ₁₁₃₃ = G ₂₂₃₃ = 2 л J a r ² x ²{[( d + e )(1 - x ²) + 2 fr ² x ²] x x [ f (1 - x ² ) + hr ² ; c ²] - g ² r ² x ² (1 - x ² )} dx ;

(2.1)

G 3311 = G 3322

= 2 ~ J a (I - x ² )[ d (1 - x ² ) + fr ² x ² ][ e (1 - x ² ) + fr ² x ² ] dx ,

G 1212    2 ^Л

J a (1 - x ² ) ² { g ² r ² x ² - ( d - e )[ f (1 - x ² ) + hr ² x ² ]} dx ,

G 1313    ^G 2323

= -2л|аgr2 x2 (1 - x 2)[ e (1 - x2) + fr2 x2] dx, где

A ^{- 1} = [ e (1 - x ² ) + fr ² x ² ]{ [ d (1 - x ² ) + fr ² x ² ] [ f (1 - x ² ) + hr ² x ² ] -

• - g ² r ² x ² (1 - x ² )}.

Ненулевые компоненты тензора упругости гексагонального кристалла, характеризуемого пятью константами,

С 1111 = C 2222 = d , C 3333 = h , C 1122 = C 2211 = d - 2 e ,

C = d — f

1133 f ,

^C 2233 = ^C 3311 = ^C 3322 = g ^{- f} ’ ^C 1212 = ^C 2121 = ^C 1221 = ^C 2112 = e ,

С = С = С = С = С = С = С =С = f

1313      3131      3232      2323      1331      3113      3223      2332 ^f •

Среди многообразия упругих констант может быть выделен подкласс, подчиняющийся условию

d = Х + 2ц, e = ц, f = цр, g = (Х+ц)р, h = (Х + 2ц)р2,     (2.2)

для которого можно ожидать существенного упрощения вида упругих решений. Данный подкласс является, по сути, одним из подклассов, выделенных Сен-Венаном [4] (см. также работу [5]) для ортотропных сред. Уравнения теории упругости для среды с подобными упругими свойствами могут быть получены масштабированием (с коэффициентом ц) соответствующих уравнений для изотропного тела по одной из осей, которая становится трансверсальной осью. Действительно, для данного случая подстановка выражения (2.2) в (2.1), а затем в (1.1) дает следующие ненулевые компоненты тензора Эшелби:

7 r 2р-1 [6Х + 10ц- (15Х +19 ц) r 2р]

S 1111 = ^S2222 =                 Т _w 2    1\5/2            ⁺

8( Х + 2 ц )( r ² р- 1)

r ²р [ - 4 ц + (9 Х + 13 ц ) r ²р ^ arctg(7 r ²р- 1) 8( Х + 2 ц )( r ²р- 1) ^5/2

У = У 1122      2211