Некоторые модификации цифрового коррелятора для обнаружения объектов на изображении

Обнаружение объектов - одна из часто встречающихся задач цифровой обработки изображений в самых различных практических приложениях [1,2]. Суть ее в том, чтобы определить координаты объектов заданного вида в плоскости исследуемого изображения, представленного своей двумерной функцией яркости. Наиболее известным и хорошо изученным является корреляционный метод обнаружения. Он основан на вычислении значений взаимной корреляции между анализируемой функцией яркости и заданным "эталоном", который, последовательно смещаясь, занимает все возможные положения в области определения функции. Для изображения, заданного двумерной сеткой отсчетов яркости, эта процедура описывается выражением:

B(m,n) = Е Е T(k,l)x(k + m, 1 + n),                                      (1)

(k,l) €D где

D — "окно" обработки, определенное относительно начала координат;

Т(к,1) - "эталон", искомый объект, заданный в области D; не умаляя общности изложения, положим, что его "центр тяжести" совмещен с началом координат, то есть

Е Е к • Т(к,1) = Е Е 1 • Tik,l) = 0.                                   (2)

(к,1)GD              (к,1) С О

х(к+т, 1+п) при (к,1) СВ- фрагмент поля яркости, соответствующий окну обработки, сдвинутому в точку (ir.,nl ;

B(m,n) - формируемое дискретное поле значений взаимной корреляции; k,l,m,n - целочисленные аргументы введенных функций.

После сравнения значений поля В с некоторым порогом выделяются области достаточно больших локальных максимумов корреляционного поля. Эти максимумы ("корреляционные пики") отмечают наиболее вероятные положения обнаруживаемых объектов в плоскости изображения, однако искомые координаты, как правило, не удается определить с достаточной точностью. Данный недостаток корреляционного метода обусловлен совместным влиянием случайного шума, присутствующего на реальных изображениях, и размытости получаемых корреляционных пиков из-за ненулевой площади объектов и их искажений типа дефокусировки, смаза и т.п. Ниже рассматриваются две модификации корреляционного метода, повышающие томность определения координат объектов при их обнаружении.

Пиковая Фильтрация корреляционного поля

Упомянутая выше пороговая обработка корреляционного поля еще не дает окончательного решения задачи обнаружения, поскольку выделяемые области локальных максимумов, как правило, оказываются пространственно протяженными. Реализация дополнительных операций анализа этих областей и определения их центров существенно усложняет цифровое устройство корреляционного обнаружения объектов (коррелятор) . Предлагаемый несложный алгоритм обработки корреляционного поля, названный "пиковым фильтром", позволяет упростить процедуру обнаружения и одновременно повысить точность определения координат локальных максимумов.

Пиковый фильтр является представителем известного класса алгоритмов ранговой обработки изображений [З,**]- В ранговых алгоритмах каждое выходное значение поля (обозначим его как В*(ш,п))вычисляется на основе анализа вариационного ряда, построенного из отсчетов некоторой окрестности соответствующей точки входного поля:

{Br) (m,n) =v[{B(m+k, п+1)}, (k,D6G])                                 (3)

В*(т,п) = Ф[(ВГ}(т'п)],                                                      <4>

G - "окно" обработки рангового алгоритма, определенное относительно начала координат (причем (0,0) GG);

V - оператор построения вариационного ряда, то есть сортировки отсчетов, указанных в аргументе, в порядке неубывания значений;

{В^}(m'n) _ вариационный ряд (множество упорядоченных и перенумерованных отсчетов), построенный для окна обработки с центром, перенесенным в точку (m,n);

г - ранг (номер) отсчета в вариационном ряду, 1< г 2 N^, где N^ - число отсчетов в окне G;

Ф - оператор вычисления выходного значения поля по вариационному ряду.

Пусть в вариационном ряду (3) г₀ - ранг отсчета B(m,n). Тогда для пикового Фильтра выражение (U) записывается в конкретном виде:

ВГо

О

г. = N B(m,n) г = N

В*(m,n)

G =                     G                                  (5)

^ro <  ^Ng [°          ^Го < ^NG •

Иными словами, входной отсчет пересылается на выход без изменения, если в вариационном ряду, построенном по его окрестности, он имеет наивысший ранг;

в противном случае отсчет выходного поля получает нулевое значение.

В результате пиковой фильтрации корреляционного поля на нем остаются ненулевыми только те точки, которые соответствуют локальным максимумам, отстоящим друг от друга на расстояние, превышающее "радиус" окна G. Очевидно, что для уменьшения числа лишних пиков размеры области G должны быть как можно больше, с другой стороны они ограничиваются сверху априорными сведениями о минимальном расстоянии между обнаруживаемыми объектами.

Положительный эффект от применения пиковой фильтрации в корреляторе демонстрируется на рис. 1. На рис. 1а представлен исходный корреляционный сигнал (для простоты иллюстрации он взят одномерным). Непосредственная пороговая обработка сигнала

С(п)

В(п) > 3

В(п) < 3

приводит его к виду, показанному на рис. 16; полученная двоичная последовательность требует дополнительной обработки для определения центров выделенных серий единиц. Пиковый фильтр с симметричным окном в пять отсчетов, примененный к сигналу, изображенному на рис. 1а, оставляет в нем лишь разнесенные локальные максимумы (рис. 1в). Отметим, что из двух близко расположенных максимумов (В(2) и

В(4)) выделяется один, больший по значению. Дальнейшая пороговая обработка 1    В*(п) £ 3

С*(п)

В*(п) < 3

непосредственно выявляет координаты наиболее значимых локальных максимумов.

Ниже при обсуждении вариантов построения коррелятора будем полагать, что корреляционное поле всегда обрабатывается пиковым фильтром.

В(П)

»*<">*

5 4

3 2

С(п).

О 2

5-4.

3-

2-1"

С*(п)

О 2

О 2

Рис. 1. Пороговая обработка и пиковая фильтрация корреляционного сигнала

Корреляционный метод с адаптивным целеуказанием

Как следует из выражения (1), в традиционном корреляционном методе вычисленные значения взаимной корреляции относятся к началу системы координат, связанной с окном обработки (то есть в соответствии с (2), к "центру тяжести" эталона в каждом его положении на плоскости). Предлагается модификация процедуры формирования корреляционного поля, заключающаяся о переходе к адаптивному целеуказанию,

при котором вычисленное для каждого положения окна значение корреляции может быть отнесено к произвольной точке окна. Конкретно, будем относить значение корреляции к "центру тяжести" поля яркости в пределах окна, то есть не к точке (m,n), как в традиционном методе, а к точке (m',n'), где

Е Е kx(k+m, 1+n)                Е Е lx(k+m, 1+п)

т . (к,1) е D                    .   . .    4. G D т = т + ------------------------- ; n = п + —'--------------------- (6)

Е Е х(к+т, 1+n)                 Е Е х(к+т, 1+п)

(к,1)€ D                              (к,1) е D

(для цифрового коррелятора значения т* , п', естественно, берутся округленными до целых) .

При наличии объекта весьма вероятно, что значения т' , п' будут одинаковы при нескольких соседних положениях эталона. Это явление положительно влияет на результаты формирования поля корреляции, поскольку ведет к значительному "обострению" корреляционных пиков. С другой стороны, оно порождает проблему композиции нескольких значений корреляции, отнесенных к одной и той же точке изображения. В качестве решений этой проблемы предлагается использовать сумму или максимальное значение корреляций. В этих двух случаях корреляционное поле, получаемое при адаптивном целеуказании - B**(p,q), может быть описано соответственно выражениями:

B**(p,q) = Е Е B(m,n) • 6(p-m', q-n')                                     (7)

(m,n)

или

B**(p,q) = max [в(m,n)6(p-m', q-n1),                                          <8)

(m, n)

где

B(m,n) - значение корреляции, вычисленное по формуле (1);

6(p-m1,

q-n')

- двумерный символ Кронекера:

6(p-m',

q-n1) =

О

p=m* и q=n'

p#m' или q#n'

m',n' зависят от m,n по формуле

(6) .

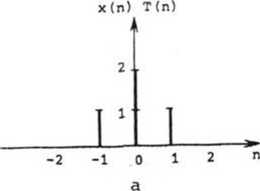
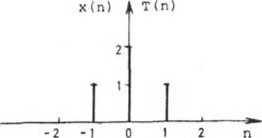
На рисунках 2, 3 дан простой пример обработки одномерного сигнала традицион ным и модифицированным корреляторами. На рис. 2а,

За показаны обрабатываемый

(-1,0,1) эталон. Согласно

дискретный сигнал и совпадающий с ним на окне D принципу действия обычного коррелятора, сдвиги эталона порождают набор значений его взаимной корреляции с сигналом (рис. 26); эти значения адресуются координатам "центра тяжести" эталона при соответствующих положениях окна и в своей совокупности образуют выходной корреляционный сигнал (рис. 2в). В корреляторе с адаптивным целеуказанием вычисленное для каждого положения окна обработки значение корреляции относится к "центру тяжести" участка анализируемого сигнала, охватываемого окном (рис. 36). В результате, как видно из рис. Зе, получается более узкий корреляционный пик (показано формирование выходного сигнала с выбором максимального значения корреляции по формуле (8)).

Экспериментальное исследование методов обнаружения

Для сравнения различных корреляционных методов обнаружения произведено их моделирование на ЭВМ. При моделировании использовались три двумерных эталонных объекта: крест единичной яркости, заданный на нулевом фоне, размером 9:9 отсче тов (рис. М , тот же крест после линейного сглаживания (усреднения) по области

а

б

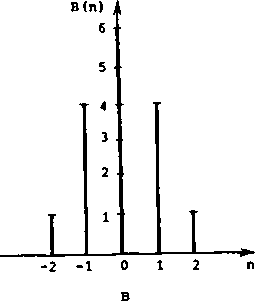
Рис. 2. Формирование корреляционного сигнала при традиционном методе обнаружения

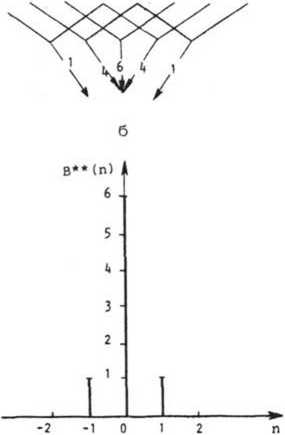
Рис. 3- Формирование корреляционного сигнала при модифицированном методе обнаружения

XXX

XXX

Рис. 4. Эталонный объект для исследования алгоритмов обнаружения

5:5 и крест, сглаженный дважды. 8 каждом случае окно обработки D представляло собой квадрат, имеющий размеры 16:16. Обрабатываемое тестовое изображение строилось путем многократного повторения выбранного эталона с шагом в 16 отсчетов по вертикали и горизонтали с последующим наложением аддитивного дискретного белого шума с нулевым математическим ожиданием и среднеквадратическим отклонением о.

Вычислительный эксперимент заключается в Формировании корреляционного поля тем или иным методом обнаружения (то есть в соответствии с формулами (1), (7) или (8)), в обработке полученного поля пиковым фильтром (5) с окном обработки G размером 10:10 отсчетов и в пороговом отборе наибольших по величине корреляционных пиков. Для каждого значения порога подсчитывалось число обнаруженных объек- тов К5 (объект считался обнаруженным, если отклонение координаты выделенного корреляционного пика от положения "центра тяжести" объекта не превышало d; рассматривались случаи d=0 и d=1) , число необнаруженных объектов К2 и число ложных объектов (лишних корреляционных пиков) К3. Экспериментально подбирался порог.

максимизирующий отношение к1

К1 + Ка + К3 имеющее смысл доли правильно обнаруженных во всей совокупности истинных и ложных объектов. Максимум величины (9) * ^тах рассматривался как показатель эффективности метода обнаружения.

На рис. 5 представлены зависимости Ртах от уровня шума на обрабатываемом изображении для различных вариантов корреляционного метода обнаружения, трех типов объектов и двух значений параметра d. Результаты экспериментального иссле дования показывают хорошую работоспособность предложенных модификаций корреляционного метода обнаружения. По сравнению с традиционным построением коррелятора адаптивное целеуказание обеспечивает более высокое качество обнаружения

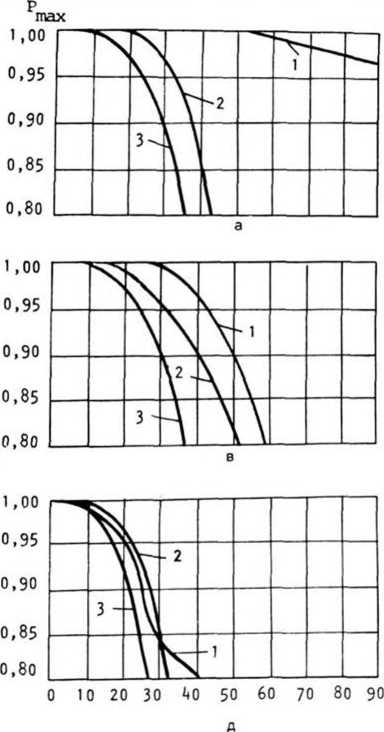
Рис. 5. Результаты экспериментального исследования корреляционных методов обнаружения: 1 - традиционный; 2 - с адаптивным целеуказанием и суммированием значений корреляции;

3 - с адаптивным целеуказанием и выделением максимального значения корреляции:

исходный объект при d = 0 (а); d=1 (б): объект, сглаженный один раз, при d=0 (в); d=1 (г); объект, сглаженный дважды, при d=0 (д); d=l (е)

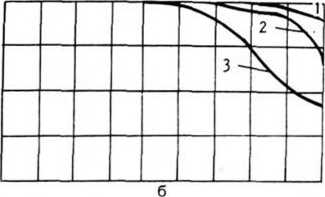
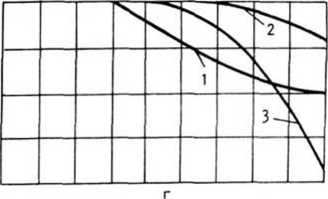
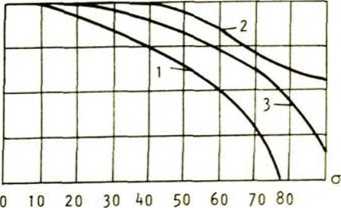
для сильно сглаженных и зашумленных объектов (то есть в ситуации, наиболее часто встречающейся на практике). Из двух рассмотренных способов формирования корреляционного поля в методе с адаптивным целеуказанием предпочтение следует отдать способу с суммированием значений корреляции.